基于无迹粒子滤波的飞行器再入段传递对准方法
张 峰,黄继勋,王颂邦
(北京航天时代光电科技有限公司,北京 100094)
基于无迹粒子滤波的飞行器再入段传递对准方法
张 峰,黄继勋,王颂邦
(北京航天时代光电科技有限公司,北京 100094)
针对再入式飞行器再入返回前需要精确和快速的传递对准需求以及空间环境特殊性,提出了一种适用于再入式飞行器空间平台对准方法,建立J2000坐标系下光纤陀螺惯组的系统状态方程,利用星敏感器输出的姿态和光纤陀螺惯组输出的姿态差值作为观测量,实现飞行器的“姿态”匹配传递对准算法。针对系统状态方程和量测方程的非线性特性以及单独使用无迹卡尔曼滤波(UKF)方法存在滤波不稳定性和单独使用粒子滤波(PF)方法存在粒子退化导致估计误差变大的问题,提出了无迹粒子滤波(UPF)算法,采用卫星工具包(STK)软件模拟飞行器在轨运行进行仿真验证。仿真结果表明:该方法可以在3s内使得失准角的估计误差小于0.6′,估计精度提高了30%,收敛时间缩短了70%,相比传统方法提高了对准的精确性和快速性。
再入式飞行器;传递对准;空间平台;无迹卡尔曼滤波;粒子滤波
再入式飞行器因其具备强大的突防能力和可重复使用的优势,作为高新科技发展的标志,在我国国防和经济建设中扮演着极为重要的角色。飞行器在再入前需要通过传递对准方式获得高精度的姿态信息。传递对准的速度和精度决定了飞行器的响应速度和精度。飞行器再入阶段的传递对准属于空间平台的动基座对准方式。
光纤陀螺惯组和星敏感器是飞行器上最重要的传感器。近几年,有不少学者提出利用星敏感器辅助陀螺惯组传递对准。马闪等用弹载星敏感器引入的位置和姿态角信息,建立“位置+姿态角”匹配的对准方法,实现了对天基导弹的精对准。印度Chaudhuri等学者建立了NWV(North West Vertical)坐标系下空间机动平台的传递对准模型。胡正东博士等人研究了空间平台下武器系统传递对准的机动方案,在当地水平坐标系下建立了21维传递对准模型,选取了“速度+姿态”匹配的方案进行了仿真。上述文献对空间平台下的传递对准技术开展了研究工作,但存在一定的局限性:由于空间环境具有微重力等特点,此时,引力提供了其轨道运行加速度,此时加速度计的输出为其自身的测量噪声和向心加速度,因此,传统的 “位置+姿态角”或“速度+姿态角”的匹配模型并不能适应于空间平台的传递对准;相对于NWV坐标系,采用J2000坐标系更能适用于空间平台传递对准坐标系;另外上述文献未考虑飞行器传递对准模型为非线性,传统滤波方法线性化处理会造成滤波器精度降低且滤波稳定性也难以保证。
基于上述情况,本文提出了以J2000惯性坐标系为导航系的星敏感器辅助的飞行器再入阶段传递对准方法,利用星敏感器的高精度姿态信息修正光纤陀螺惯组的误差。针对模型的非线性化,单独使用 UKF存在滤波不稳定和使用 PF方法存在粒子退化导致估计误差变大的问题,提出了 UPF滤波方法,通过将UKF作为其重要性分布函数来解决粒子退化问题,相比单独使用UKF或PF方法,在传递对准时间和精度上都有很大的提高。
1 飞行器再入段传递对准模型
1.1 传递对准方案
利用星敏感器测量恒星天体位置与飞行器相对位置,获得飞行器的姿态信息,并与光纤陀螺惯组输出的姿态信息进行比较,得到飞行器的姿态角误差,作为量测量。建立光纤陀螺惯组在空间平台下的系统误差方程,通过滤波估计将数学平台偏离导航坐标系的失准角估计出来,校正飞行器的数学平台使之与导航坐标系精确对准,对准方案如图1所示。

图1 空间平台传递对准方法Fig.1 Alignment method on space platform
1.2 系统误差方程
传递对准误差方程包括姿态误差方程、速度误差方程和位置误差方程,以下建立J2000地心惯性坐标系(i系)下有关导航系统误差方程。
1.2.1 姿态误差方程
姿态误差方程可表示为


式(8)为惯性坐标系下的姿态失准角误差方程,该式表明:惯性坐标系下的捷联惯导系统姿态失准角误差是由载体陀螺仪的角速度误差所引起的。
1.2.2 速度误差方程
考虑飞行器在轨运行,由地球自转引起的向心加速度以及哥氏加速度的影响,速度误差方程为:


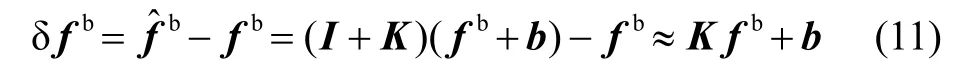
式中,K=diag(kx,ky,kz)为加速度计输出的比力标度因数误差阵,b为加速度计零位误差。δGi如下式所示:

式中:GM为万有引力常数与地球质量乘积,GM=398600.5e9m3s2;r为地球半径, r=6371km。结合上述式(5)(11)(12)可得:

式中,ΔGi表示引力扰动矢量。化简得速度误差微分方程:

式中,Fi为fi的反对称阵。
1.2.3 位置误差微分方程
惯性坐标系下位置误差微分方程由位置方程得到,如下式所示:

1.3 状态方程
为了提高传递对准速度,必须对全阶状态方程的维数进行降维处理,否则将会给光纤陀螺惯组的计算带来很大负担,但又必须保证对准精度,因此,设计了9维传递对准模型。
离散的状态方程可以描述为1.4 量测方程

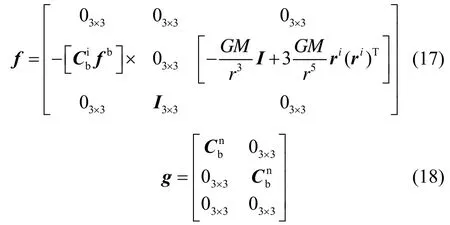

式中,v为姿态角量测噪声,v~N(0,R)。建立姿态角误差观测量[δθδγδψ]与系统状态模型中的状态变量之间的关系,设姿态转换矩阵T为

易得:

由(20)和(21)可得:
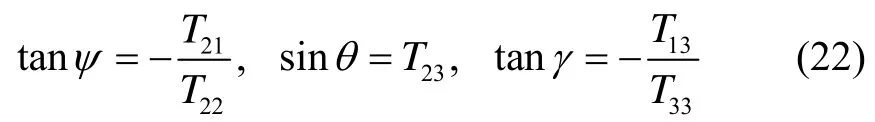
将式(22)左端按照一阶泰勒展开可得:
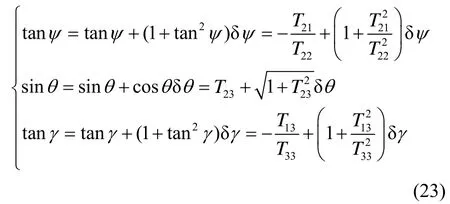
再由式(22)可得:

由式(23)和式(24)可得:
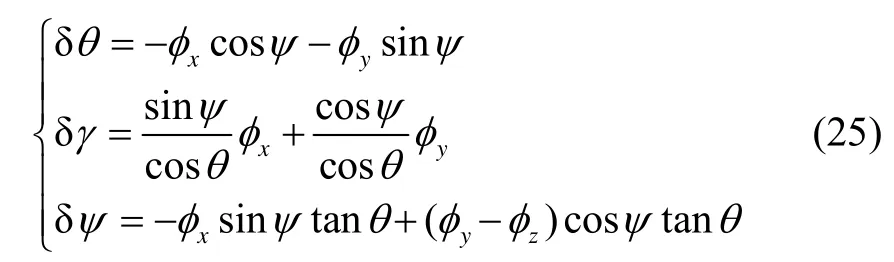
则姿态角匹配的测量矩阵为

从上述状态方程和量测方程推导结果来看,系统状态方程和量测方程均为非线性方程,本文针对方程非线性的问题,提出了UPF滤波算法。
2 UPF空间平台传递对准滤波算法
2.1 算法思路
无迹卡尔曼滤波(UKF)是采用逼近非线性函数概率密度分布的滤波方法。其核心是UT变换,即根据先验分布采样一组确定的Sigma点,这些点保留了原状态变量的先验分布特性;将这些点通过非线性函数传播,对所得结果作加权回归运算使其逼近非线性状态后验分布。然而,当 Sigma点采样涉及协方差阵的平方根运算时,数值计算中的舍入误差会破坏协方差阵的非负定性和对称性,降低滤波算法的稳定性。同时,高阶矩阵的平方根运算也将导致系统的计算负担增加。
粒子滤波(PF)具有非常好的处理非线性模型的能力,鲁棒性强,但存在粒子退化的问题,经过几步迭代递推之后,许多粒子的权重变得非常小,它们在获得估计值过程中起到的作用将变得微乎其微,可以称之为无效粒子。
结合UKF和PF的优势,取长补短,采用了UPF算法,其思路则是通过UKF 算法设计重要性函数,产生粒子。首先利用UKF实时的进行状态的均值和方差估计,以作为PF粒子采样的重要性函数,从而可以将采样粒子从高先验密度区向高似然密度区移动。
2.2 UPF算法流程
建立离散时间系统状态空间模型:

具体解算流程如下:

式中,i=1,…,n。由系统状态方程为n=9维变量,故sigma采样点个数为2n+1=19。对应的权值为:
一阶统计量权值:
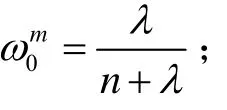
二阶统计量权值:

式中:λ为比例因子;κ在多维状态变量下通常取为κ=3;α决定采样点与均值的离散程度,通常取α=0.01;β用来描述的分布信息,通常取β=2;为协方差加权,为均值加权。
3)时间更新:
4)量测量更新:

5)更新sigma点:
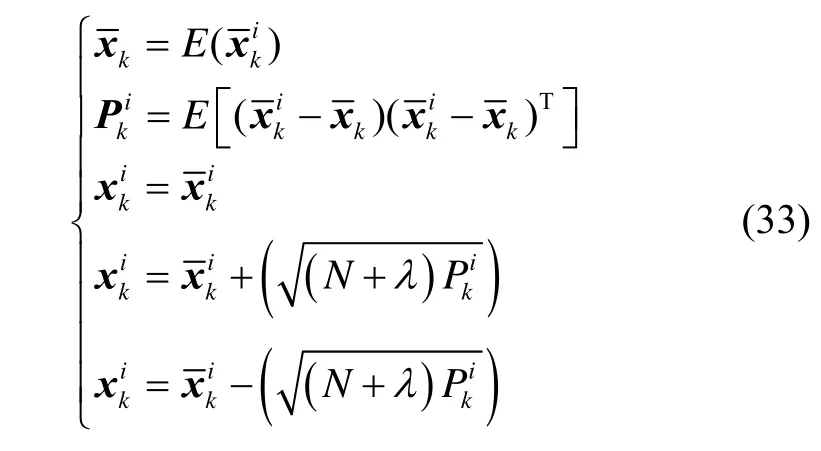
6)重要性采样,并计算重要性权值:
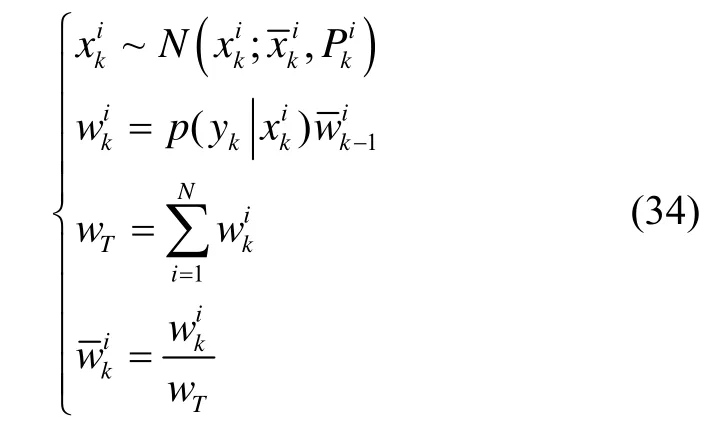
7)计算估计误差,定义Neff来衡量有效粒子数量并运用重采样算法对加权粒子进行重新采样。
8)更新估计值:
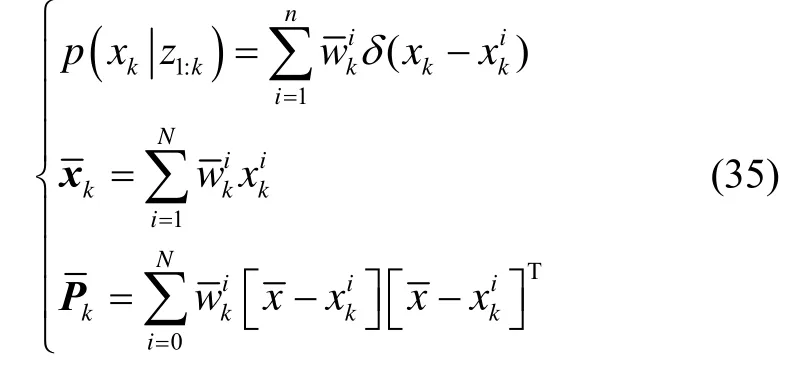
该算法改进了一般PF滤波方法中重要性函数的选择策略,有利于将采样粒子从高先验密度区向高似然密度区移动,可以提高滤波精度,同时又避免了UKF线性化带来的滤波不稳定性的问题。
算法具体流程如图2所示。

图2 算法流程图Fig.2 Flowchart of the algorithm
3 仿真与试验
仿真过程采用STK软件来仿真空间平台轨道数据[12-14],轨道参数为:近地点距离300km,远地点距离350km,轨道倾角15°。选择J2000坐标系,定义oxyz为飞行器本体坐标系,其中:ox轴通过坐标原点,指标飞行器飞行方向;oy轴按照右手定则,垂直轨道面方向;oz轴指向地心方向。飞行器仿真轨迹为绕oz轴座摇摆机动运动,最大摇摆角度为2°,摇摆周期为1s。
根据卫星运动轨迹参数,可得到飞行器理论的姿态四元数和姿态角信息。对光纤陀螺惯组误差参数定义如下:X轴方向失准角xφ为4°,Y轴方向失准角yφ为5°,Z轴方向失准角zφ为10°。光纤陀螺惯组的性能参数如表1所示。

表1 光纤陀螺惯组的性能参数Tab.1 Parameter specification of slave FOG IMU
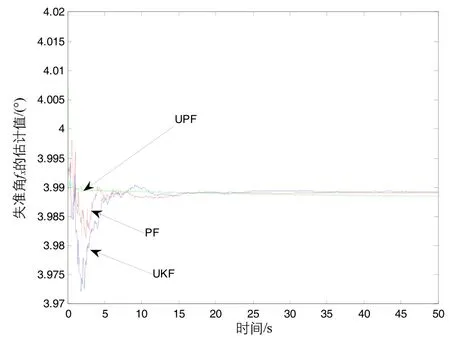
图3 X轴失准角估计曲线Fig.3 Estimation curve of X-axis misalignment
仿真滤波初值设定:状态变量X初始值均取为0,初始方差阵的对角线元素取P(0)=103Ι9×9,姿态角量测噪声方差阵取R=0.01·Ι3×3,光纤陀螺惯组姿态更新时间为10ms,星敏感器更新时间为250ms,滤波周期为250 ms,N=300,Nthr=100,仿真时间为50 s。图3~图5为三轴失准角的估计结果。由图3~图5所示以及表2失准角估计误差结果可知,本文提出的基于无迹粒子滤波方法比仅用粒子滤波或无迹卡尔曼滤波可以在3 s内使得失准角估计误差达到优于0.6′,估计精度方面提高了30%,收敛时间缩短了70%。

图4 Y轴失准角估计曲线Fig.4 Estimation curves of Y-axis misalignment

图5 Z轴失准角估计曲线Fig.5 Estimation curves of Z-axis misalignment
表2为失准角的估计值。图6为三个轴失准角角度的估计误差曲线。

表2 失准角估计误差Tab.2 Estimation errors of three-axis misalignments

图6 三轴失准角估计误差Fig.6 Estimation errors of three-axis misalignments
4 结 论
针对再入飞行器再入段环境的特点,提出 J2000惯性坐标系下基于星敏感器和光纤陀螺惯组“姿态”匹配的传递对准方法,建立了光纤陀螺惯组的系统状态方程,利用星敏感器输出的姿态和光纤陀螺惯组输出的姿态差值作为观测量,实现飞行器的传递对准。针对系统状态方程和量测方程的非线性特性,提出了无迹卡尔曼滤波和粒子滤波相结合滤波算法,采用STK软件模型飞行器在轨运行进行仿真验证。仿真结果表明:该方法可以在3 s内使得失准角估计误差达到优于0.6′, 估计精度提高了约30%,收敛时间缩短了70%,相比传统方法提高了仿真验证了该算法的有效性,精确性和快速性。该方案同样适用于其他飞行器的传递对准,具有较好的参考价值。
(References):
[1] 戴晨曦, 程向红, 陈红梅, 等. 天文观测角辅助的高超声速飞行器传递对准方法[J]. 中国惯性技术学报, 2015, 23(4): 446-450. Dai Chen-xi, Cheng Xiang-hong, Chen Hong-mei, et al. Transfer alignment approach of hypersonic vehicle aided by celestial angle[J]. Journal of Chinese Inertial Technology, 2015, 23(4): 446-450.
[2] 胡正东, 杨华波, 张士峰, 等. 空间平台武器系统传递对准的机动方案设计[J]. 中国惯性技术学报, 2007, 15(4): 398-402. Hu Zheng-dong, Yang Hua-bo, Zhang Shi-feng, et al. Maneuvering scheme of transfer alignment for weapon system on space platform[J]. Journal of Chinese Inertial Technology, 2007, 15(4): 398-402.
[3] 梁冬生, 刘朝晖, 刘文, 等. 航空飞行器天文自主导航定位技术[J]. 红外与激光工程, 2014, 43(9): 3020-3025. Liang Dong-sheng, Liu Zhao-hui, Liu Wen, et al. Aerial vehicle astronomy autonomous navigation technology[J]. Infrared and Laser Engineering, 2014, 43(9): 3020-3025.
[4] Wang Rong, Xiong Zhi, Liu Jian-ye, et al. SINS/GPS/CNS information fusion system based on improved Huber filter with classified adaptive factors for high-speed UAVs[C]// IEEE/ION Position Location and Navigation Symposium. 2012: 441-446.
[5] Zhang Jin-liang, Qin Yong-yuan, Wu Feng. Technique for in-flight calibrating installation errors in multi-IMU redundancy system[C]//Proceedings of the 2012 International Conference on Information Technology and Software Engineering. 2012: 99-108.
[6] 何小飞, 王巍, 黄继勋. 联邦滤波在光纤陀螺捷联惯导系统传递对准中的应用[J]. 红外与激光工程, 2013, 42(4): 993-997. He xiao-fei, Wang Wei, Huang Ji-xun. Application for transfer alignment of FOG SINS based on federated filter [J]. Infrared and Laser Engineering, 2013, 42(4): 993-997.
[7] Richman M S, Kenyon J A, Sega R M. High speed and hypersonic science and technology[C]//2005 AIAA Guidance, Navigation and Control Conference and Exhibit. San Francisco, CA: AIAA 2005-4099.
[8] Bahm C, Baumann E. The X-43A Hyper-X Mach 7 Flight 2 guidance, navigation and control overview and flight test results[C]//AIAA/CIRA 13thInternational Space Planes and Hypersonics Systems and Technology: AIAA 2005-3275.
[9] 吴枫, 秦永元, 成研, 等. 基于GPS的弹载捷联惯导动基座传递对准技术[J]. 中国惯性技术学报, 2013, 21(1): 56-60. Wu Feng, Qin Yong-yuan, Chen Yan, et al. Transfer alignment for missile-borne SINS using airborne GPS on moving base[J]. Journal of Chinese Inertial Technology, 2013, 21(1): 56-60.
[10] Lai Ji-zhou, Xiong Jian, Liu Jian-ye, et al. Improved arithmetic of two-position fast initial alignment for SINS using unscented Kalman filter[J]. International Journal of Innovative Computing, Information and Control, 2012, 8(4): 2929-2940.
[11] Ilewicz W, Nawrat A. Direct method of IMU calibration. In: Advanced technologies for intelligent systems of national border security studies in computational intelligence[M]. Springer, Heidelberg, 2013: 155-171.
Transfer alignment for reentry spacecraft based on unscented particle filter in space platform
ZHANG Feng, HUANG Ji-xun, WANG Song-bang
(Beijing Aerospace Times Optical-Electronic Technology Co., Ltd., Beijing 100094,China)
A transfer alignment method for reentry spacecraft in view of the space environment’s particularity is proposed to serve the need of rapid and precise transfer alignment. The state and measurement equations of the fiber optic gyroscope inertial measurement unit (FOG IMU) are established, and by using the output attitude difference between the outputs of FOG IMU and star sensor, a transfer alignment algorithm is achieved. Since only using UKF has the problems of filtering instability, and only using PF has the problems of particle degradation, an algorithm based on unscented particle filter (UPF) method is presented on account of the nonlinear feature of the state and measurement equations. Simulations are made by using a satellite tool kit (STK) tool to simulate the spacecraft its operations on-orbit, which show that, compared with its traditional method, the misalignment estimation can converge to 0.6 arcmin within 3 s, the estimation accuracy is increased by 30%, and convergence time is shorten by 70%。
reentry spacecraft; transfer alignment; space platform; unscented Kalman filter; particle filter
U666.1
:A
2016-04-11;
:2016-07-28
国家高技术研究发展计划项目(863-706)(2013AA706503)
张峰(1982—),男,高工,博士研究生,从事导航、制导与控制技术研究。E-mail: guyansnow@126.com
1005-6734(2016)04-0443-06
10.13695/j.cnki.12-1222/o3.2016.04.005

