基于EMD及灰色关联度的滑动轴承润滑状态故障诊断研究

卢绪祥，　苏一鸣，　吴家腾，　李录平

(长沙理工大学 能源与动力工程学院，长沙 410114)



基于EMD及灰色关联度的滑动轴承润滑状态故障诊断研究

卢绪祥，苏一鸣，吴家腾，李录平

(长沙理工大学 能源与动力工程学院，长沙 410114)

摘要：针对滑动轴承润滑状态发生改变时，其声发射信号不同频带的能量分布与其润滑状态之间存在一定的映射关系，提出一种经验模态分解(EMD)与加权灰色关联分析相结合的诊断方法.采用EMD方法将滑动轴承非平稳声发射信号分解为有限个平稳的本征模态函数(IMF)，依据相关系数法剔除IMF分量中的虚假分量，选取包含主要故障信息的前10阶IMF分量计算能量比例，并构造特征向量.结果表明：加权灰色关联分析对小样本模式识别具有良好的分类效果；通过加权灰色关联分析计算不同声发射信号的灰色关联度，能够有效地对滑动轴承的润滑状态进行诊断.

关键词：滑动轴承； 故障诊断； 经验模态分解； 能量比例； 加权灰色关联分析； 熵权法

滑动轴承是大型旋转机械的重要支撑部件，其理想工作状态是流体润滑状态，但是由于载荷重、工作环境复杂，很容易发生润滑状态故障，尤其是在半干摩擦状态的初发阶段，油膜的减振作用使通过的振动信号很难检测，如何在高转速和高背景噪声环境下对滑动轴承的运行状态进行监测是工程应用中需要解决的难题之一.

相比振动信号，声发射信号能迅速反映运行状态的变化，更适用于早期故障的检测[1].作为典型的非平稳信号，声发射信号的故障特征提取方法一直是研究的难点.自适应性时频分析方法是处理非平稳信号的最佳工具[2]，目前最具代表性的方法之一便是经验模态分解(EMD)方法，该方法采用不断减去信号局部均值曲线的迭代方式以获得瞬时频率具有物理意义的分量[3-4]，将信号自适应地分解成若干平稳的基本模式分量，但是由于算法本身的缺陷，分解结果中可能产生虚假的本征模态函数(IMF)[5].EMD方法在机械故障诊断方面的应用主要针对滚动轴承和齿轮的振动信号，最常见的处理方式是将EMD方法与其他技术相结合，提取故障频率及其他特征信息[6-9]，目前针对滑动轴承声发射信号方面的研究还鲜见报道.相对于滚动轴承，滑动轴承声发射的工况更加复杂，且不具有明显的周期性，不能简单地通过突变时的频率和幅值变化来判断故障[10].但是当滑动轴承发生润滑状态故障时，与正常信号相比，故障信号相同频带内的能量会存在较大的差别，这些频带内的信号能量包含主要故障信息，某一个或几个频带内的信号能量改变即代表了一种故障，因此可以以频带能量为依据，根据其变化情况来进行分析.

基于以上情况，笔者从滑动轴承声发射信号能量分布出发，提出了基于EMD与加权灰色关联分析相结合的滑动轴承状态诊断方法.首先对信号进行EMD分解，采用相关系数法剔除声发射信号的IMF虚假分量，计算包含主要故障信息的IMF分量的能量比例，以能量比例为元素构造标准模式特征向量，然后计算标准模式与待识别模式之间的灰色关联度来判断轴承的工作状态.为了改善传统灰色关联分析未考虑各指标权重的缺点，采用熵权法来确定各指标的权重，提高识别的精度和准确度.

1经验模态分解

1.1原理和算法

EMD方法的提出基于以下假设：任意一个信号都可以分解成一个或多个IMF，这与快速傅里叶变换(FFT)把信号分解成正弦或余弦函数有着本质的不同.IMF必须满足以下2个条件：(1)极值点与过零点数量相等或最多相差一个；(2)任意时间上，由局部极大值点组成的上包络线和由局部极小值点组成的下包络线的平均值为零.这样IMF不再限定为窄带信号，而是幅值和频率可调制.

设被分析信号的时间序列为x(t)，其分解过程可简要描述为以下几步[3]：(1)初始化定义x(t)=x0(t)和r0(t)=x0(t)；(2)识别x(t)的所有局部极值(极大值和极小值)，将所有极大值点和极小值点分别用三次样条曲线连起来，形成上包络线Emax(t)和下包络线Emin(t)；(3)求取上、下包络线的平均值，得到均值序列m(t)=0.5×[Emax(t)+Emin(t)]；(4)定义d(t)=x(t)-m(t)，判断d(t)是否满足IMF的2个条件，如果不满足，令x(t)=d(t)，重复步骤(2)～步骤(4)，直到d(t)满足IMF的2个条件，记为c1(t)=d(t)；(5)定义x(t)=x0(t)-d(t),r1(t)=r0(t)-d(t)，重复以上步骤，依次可以得到第二、第三直到第n个IMF，记为c2(t)，c3(t)，…，cn(t)，整个处理过程在满足预定的筛选停止准则后停止，最后剩下原始信号的残余分量rn(t).

1.2虚假分量的剔除

EMD方法在分解过程中常常会由于插值误差、过分解等原因，使分解结果中出现虚假分量，这些虚假分量并不能表征原始信号，会对后续分析产生影响，需要剔除.

由于信号分解得到的IMF分量相互之间满足局部正交性，所以真实的IMF分量与原始信号之间存在较强相关性，而虚假的IMF分量则与之相反.因此，可以计算各 IMF分量与原始信号的相关系数，以此作为选取IMF分量的依据.具体过程如下：先计算各IMF与原始信号的皮尔逊相关系数Ri(i=1，2，…，n；其中i为 IMF的阶次);然后将Ri与一个阈值λ进行比较,如果Ri≥λ，则表示该IMF分量为真实IMF分量，否则就视为虚假分量.皮尔逊相关系数R的数学表达式如下：

(1)

式中：cov(X,Y)为序列X与Y的协方差;cov(X,X)和cov(Y,Y)分别为序列X和Y的方差.

R的取值范围为[-1,1]，绝对值越大表明两者间的相关性越强，即IMF分量所包含的关于原始信号的有效信息越多.

1.3EMD数值仿真

以一个具体的例子来说明采用相关系数法进行虚假分量筛选的有效性.仿真信号如下:x(t)=x1(t)+x2(t)+x3(t)；x1(t)=3sin(10πt),x2(t)=2sin(56πt),x3(t)=4sin(100πt).采样频率为1 000 Hz，采样时间为1 s.采用镜像延拓EMD方法对信号进行分解，得到4个IMF分量和1个残余分量，如图1所示.

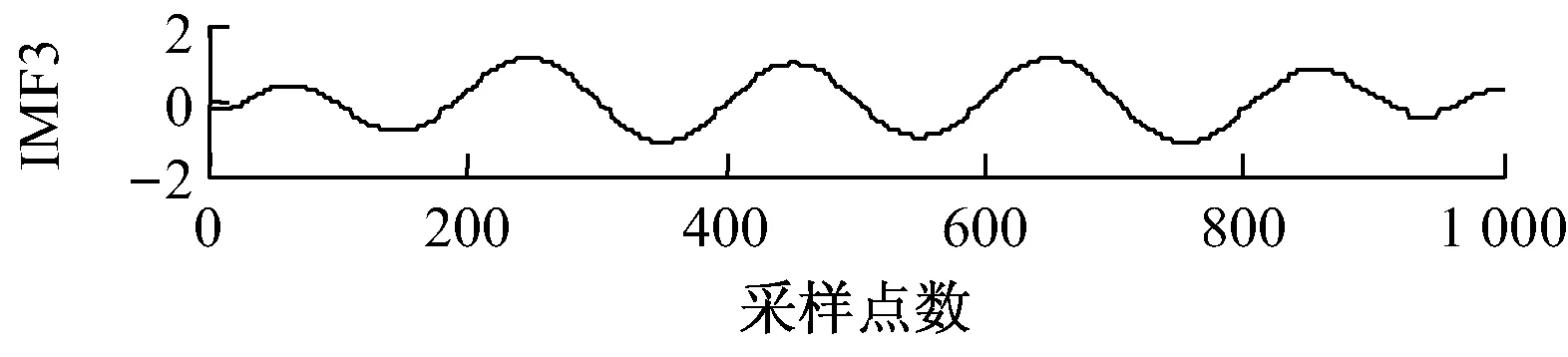
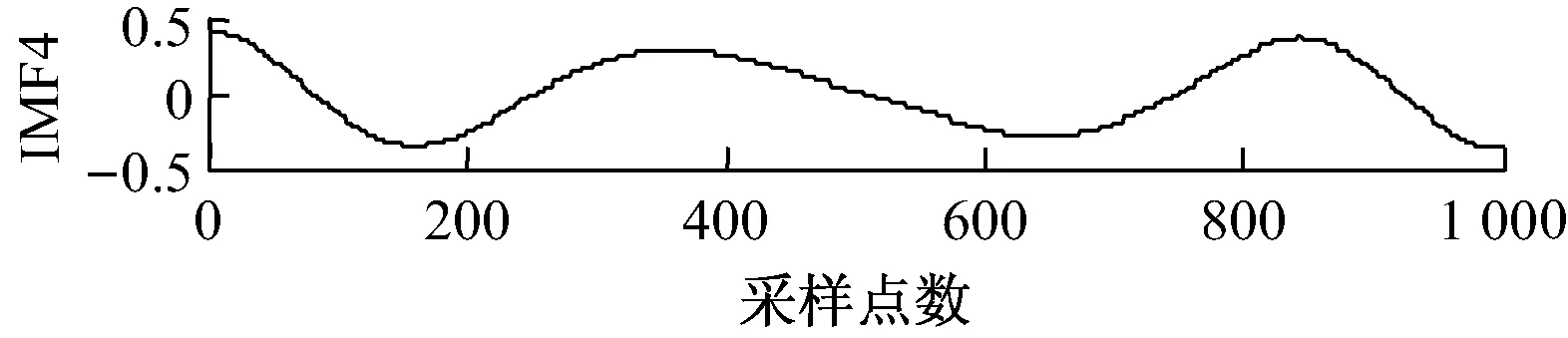
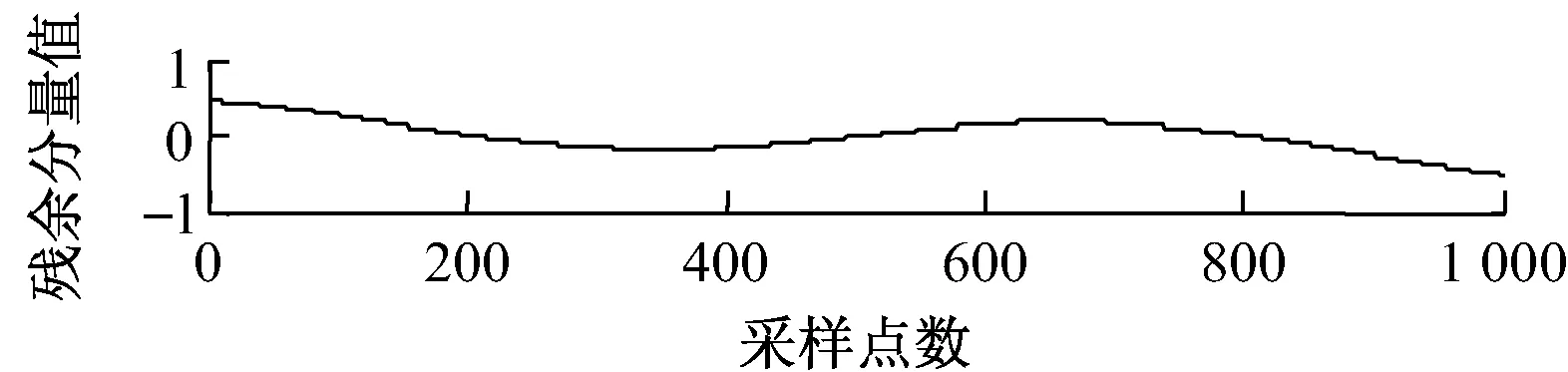
图1　仿真信号x(t)的EMD分解结果

由原始信号的表达式可知，原始信号x(t)包含3个分量，因此理论上x(t)应该被分解成3个IMF分量和1个残余分量，而实际结果中包含4个IMF分量和1个残余分量，表明实际结果中存在虚假分量.采用前文介绍的相关系数法，根据式(1)计算出各IMF分量与原始信号的皮尔逊相关系数，结果见表1.由表1可以看出，前3阶IMF与原始信号的皮尔逊相关系数较大，IMF4与原始信号的皮尔逊相关系数很小，接近0，因此可以判定IMF4分量为虚假分量，应当剔除.前3阶IMF分量为真实分量予以保留，其中IMF1分量代表x3(t)，IMF2分量代表x2(t)，IMF3分量代表x1(t)，分解结果与实际相符，表明采用相关系数法可以有效剔除EMD分解过程中产生的虚假分量.

表1　各阶IMF与原始信号的皮尔逊相关系数

2加权灰色关联分析

灰色关联分析是灰色理论进行系统分析的重要方法，根据因素之间发展态势的相似程度来衡量因素间接近的程度，本质上是几种曲线间几何形状的分析比较，即认为几何形状越接近，关联度越大.这种方法不要求样本数据有典型的规律，且计算量小，尤其适合小样本情况.

设滑动轴承的润滑状态有m种，每种状态的标准模式特征向量由n个特征参数组成，并记为xi=(xi(1),xi(2),…,xi(n))，i=1,2,…,m.设待检的特征向量为y=(y(1),y(2),…,y(n))，则待检特征向量与标准模式特征向量的关联度系数[11]为

(2)

式中：ρ为分辨系数，且ρ∈[0,1]，一般取ρ=0.5.

由此可以得到y与xi的灰色关联度为

(3)

式中：β(k)为第k个特征参数的权重.

权重的计算方法有多种，笔者通过熵权法求得，熵可以反映随机变量的不确定性信息量，利用熵权法客观赋权可以对信息进行有效利用，其结果更具有客观性[12]，具体步骤如下：

(1)对原始数据矩阵进行无量纲化处理,得到矩阵B=(bij)m×n.

(2)计算在第j个特征参数下第i种故障模式的特征比例：

(4)

(3)计算第j个特征参数的熵：

(5)

(4)确定第j个特征参数的权重：

(6)

3基于EMD能量比例与灰色关联度的润滑状态识别原理

基于加权灰色关联分析的识别流程图如图2所示，具体步骤如下：

(1)在滑动轴承流体润滑、半干摩擦和干摩擦状态下，按一定的采样频率进行多次采样.

(2)对滑动轴承声发射信号进行EMD分解，得到若干个IMF分量.

(3)通过相关系数法剔除与原始信号相关性较弱的虚假分量.

(4)计算保留的n个IMF分量的能量比例Ti.

(7)

式中：Ti为第i个IMF分量所占的能量比例；Ei为第i个IMF分量的能量.

(5)构造特征向量T=[T1,T2,…,Tn]，计算待识别模式与各标准模式之间的灰色关联度，与待识别模式灰色关联度最大的标准模式被判定为待识别模式所处的模式.

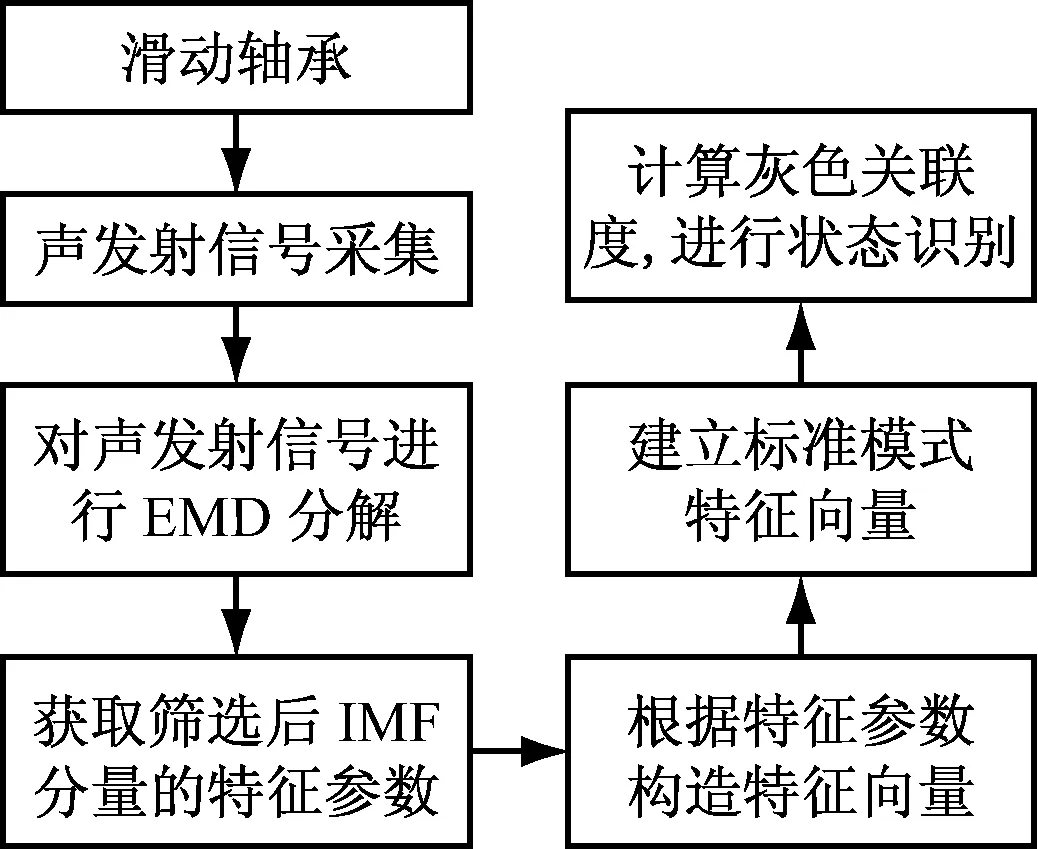
图2　基于加权灰色关联分析的识别流程图

4实验室及现场应用

4.1故障模拟

为了获得典型状态的标准模式特征向量，首先在转子实验台上进行试验，以获得不同状态下的声发射信号.在试验中，当轴承达到正常润滑状态后关闭油路停止供油，轴颈与轴瓦之间的残余油量越来越少，从而模拟润滑状态的劣化过程，为判别轴承所处的润滑状态，在轴颈与轴瓦之间构造一个测量电路，具体见图3.

图3　测量电路

图3中R1表示轴颈与轴瓦之间的油膜电阻，R2为平衡电阻.在流体润滑状态时，油膜厚度大，将轴颈与轴瓦完全分隔开，R1很大，灯泡不亮，R2两端电压接近零；停止供油后，随着时间的推移，轴颈与轴瓦之间的油量逐渐减少，油膜开始变薄，当油膜不足以将轴颈与轴瓦完全分开时，将与金属表面的微凸体发生接触，润滑状态处于半干摩擦状态，灯泡开始变红，R2两端电压逐渐增大；润滑状态继续劣化，当灯泡明显变亮，R2两端电压基本稳定时，表明发生了严重的干摩擦.

4.2标准模式特征向量的构建

对试验过程中采集的声发射信号进行EMD分解，并剔除虚假分量.以干摩擦状态下声发射信号为例，图4给出了各IMF与原始信号的皮尔逊相关系数.由图4可以看出，前10阶IMF与原始信号的皮尔逊相关系数较大，根据相关系数法可以判断，这些IMF分量均为真实分量，予以保留；后5阶IMF分量为虚假分量，应当剔除.

图4　干摩擦状态下声发射信号各IMF与

Fig.4Pearson correlation coefficient between IMFs and the original signal of acoustic emission for dry friction

对流体润滑状态和半干摩擦状态下声发射信号采用同样的方法进行处理，均保留10阶IMF分量，EMD方法是一种主成分分析方法，主要的故障信息包含在前10阶IMF分量中，所以取前10阶IMF分量，计算能量比例并构造特征向量.图5给出了滑动轴承在3种状态下的能量比例.由图5可以看出，在能量分布图中，由左向右从高频段逐渐到低频段排列，不同状态对应的能量分布有着明显的区别，在润滑状态劣化过程中，高频分量不断增加，这对于状态识别非常有利.

为避免数据选择的偶然性，选择3种状态下的信号各3组，计算每种状态下信号的IMF分量的能量比例并取平均值，作为该状态的标准模式特征向量，结果见表2.

4.3现场应用

对某电厂310 MW汽轮发电机组的汽轮机低压缸后轴承进行试验[13]，采集并保存了试验过程中的声发射信号，采样频率为3 MHz.采用所提出的方法对滑动轴承润滑状态进行诊断，先计算标准模式特征向量与待识别模式特征向量的灰色关联度，然后根据灰色关联度进行排序，从而判断轴承所处的状态.表3和表4分别给出了根据加权灰色关联分析和传统灰色关联分析得到的灰色关联度和识别结果.

(a)流体润滑状态

(b)半干摩擦状态

(c)干摩擦状态

状态特征向量T1T2T3T4T5T6T7T8T9T10流体润滑0.912.623.294.077.3822.5250.677.101.020.40半干摩擦0.152.4917.0926.828.885.6011.0721.255.920.72干摩擦0.574.0324.8228.208.104.248.7715.135.350.79

表3待识别模式与标准模式特征向量的加权

灰色关联度和识别结果

Tab.3Weighted grey incidence between identified patterns and standard as well as the identification results

样本编号γ1γ2γ3识别结果10.96130.43540.4531流体润滑状态20.88100.46730.4670流体润滑状态30.96480.40510.4171流体润滑状态40.95260.39840.4103流体润滑状态50.88340.47350.4985流体润滑状态60.38930.87520.8018半干摩擦状态70.41320.88250.7420半干摩擦状态80.40950.88500.6762半干摩擦状态90.40740.88860.8197半干摩擦状态100.40450.90910.7901半干摩擦状态110.42560.78700.8681干摩擦状态120.49290.77130.8750干摩擦状态130.44630.72450.8939干摩擦状态140.50480.74680.8805干摩擦状态150.42250.77580.9037干摩擦状态

根据识别结果，滑动轴承在试验过程中发生了磨瓦故障，从试验结束后停机解体轴承的检查结果发现，轴承确实发生了严重的干摩擦，造成轴颈和轴瓦的磨损，磨损情况见图6.

由表3可以看出，采用加权灰色关联分析对滑动轴承润滑状态故障模式识别取得了理想的效果，说明加权灰色关联分析在小样本故障识别中的有效性.通过对比表3和表4可以发现，虽然传统灰色关联分析也能对不同的润滑状态故障进行识别，但是得到的灰色关联度偏小，且灰色关联度比较接近，分布区间偏小，而采用加权灰色关联分析得到的灰色关联度更大，更能反映数据序列之间的相似程度，精度更高.

表4　待识别模式与标准模式特征向量的传统

(a)磨损轴瓦(b)磨损轴颈

图6磨损轴瓦和轴颈

Fig.6Photos of the worn bushing and journal

5结论

提出了一种基于EMD和加权灰色关联分析的滑动轴承润滑状态故障诊断方法.采用EMD方法对声发射信号进行分解，依据相关系数法剔除IMF分量中的虚假分量，获得包含主要故障信息的真实分量，进而计算各IMF分量的能量比例并构建特征向量，为故障诊断提供依据.利用加权灰色关联分析实现滑动轴承润滑状态故障信号的识别，结果表明利用本文方法进行滑动轴承润滑状态故障诊断可以获得较高的精度和准确度，对滑动轴承润滑状态故障监测与诊断具有实际的工程应用价值.

参考文献：

[1]MBA D, RAO R B K N. Development of acoustic emission technology for condition monitoring and diagnosis of rotating machines: bearings, pumps, gearboxes, engines, and rotating structures[J]. The Shock and Vibration Digest, 2006，38(1)：3-16.

[2]LEI Yaguo, HE Zhengjia, ZI Yanyang. Application of an intelligent classification method to mechanical fault diagnosis[J]. Expert Systems with Applications,2009, 36(6):9941-9948.

[3]HUANG N E，SHEN Z, LONG S R. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society A, 1998, 454: 903-995.

[4]SMITH S J. The local mean decomposition and its application to EEG perception data[J]. Journal of the Royal Society Interface, 2005,2(5):443-454.

[5]BAO Chunxiao, HAO Hong, LI Zhongxian,etal. Time-varying system identification using a newly improved HHT algorithm[J]. Computers and Structures, 2009, 87(23/24):1611-1623.

[6]张俊红，李林洁，马文朋，等．EMD-ICA联合降噪在滚动轴承故障诊断中的应用[J].中国机械工程，2013, 24(11)：1468-1472.

ZHANG Junhong, LI Linjie, MA Wenpeng,etal. Application of EMD-ICA to fault diagnosis of rolling bearings[J]. China Mechanical Engineering, 2013, 24(11)：1468-1472.

[7]时培明，丁雪娟，李庚，等．一种EMD改进方法及其在旋转机械故障诊断中的应用[J]．振动与冲击，2013,32(4)：185-190.

SHI Peiming, DING Xuejuan, LI Geng,etal. An improved method of EMD and its applications in rotating machinery fault diagnosis[J]. Journal of Vibration and Shock, 2013, 32(4)：185-190.

[8]张超，袁彦霞．频率调制经验模态分解在轴承故障诊断中的应用[J]．振动与冲击，2014，33(18): 185-189.

ZHANG Chao, YUAN Yanxia. Application of frequency modulated EMD in bearing fault diagnosis[J]. Journal of Vibration and Shock, 2014，33(18): 185-189.

[9]向玲，鄢小安．汽轮机转子故障诊断中LMD法和EMD法的性能对比研究[J]．动力工程学报，2014，34(12)：945-951.

XIANG Ling, YAN Xiaoan. Performance contrast between LMD and EMD in fault diagnosis of turbine rotors[J]. Journal of Chinese Society of Power Engineering, 2014,34(12):945-951.

[10]卢绪祥，刘雨佳，李录平，等．形态滤波在滑动轴承声发射信号降噪中的应用[J]．动力工程学报，2013，33(4)：278-284.

LU Xuxiang, LIU Yujia, LI Luping,etal. Application of morphological filtering in denoising of acoustic emission signals for sliding bearing[J]. Journal of Chinese Society of Power Engineering, 2013, 33(4): 278-284.

[11]刘思峰，郭天榜，党耀国．灰色系统理论及其应用[M]．5版. 北京: 科学出版社，2010.

[12]张浩，杨佳妮，苏翔．基于信息熵及超效率SBM模型的柔性制造系统绩效评价[J]．现代制造工程，2014(7)：16-20.

ZHAGN Hao, YANG Jiani, SU Xiang. Using entropy-based super SBM model for evaluating flexible manufacturing systems[J]. Modern Manufacturing Engineering, 2014(7)：16-20.

[13]靳攀科，李录平，谭海辉，等．310 MW汽轮发电机组启动过程中滑动轴承声发射信号特性试验[J]．汽轮机技术，2011，53(6):455-458.

JIN Panke, LI Luping, TAN Haihui,etal. Characteristics of sliding bearing acoustic emission trial during the startup of 310 MW steam turbine[J]. Turbine Technology，2011，53(6):455-458.

Fault Diagnosis on Lubrication State of Journal Bearings Based on EMD and Grey Relational Degree

LUXuxiang，SUYiming，WUJiateng，LILuping

(School of Energy and Power Engineering, Changsha University of Science and Technology, Changsha 410114, China)

Abstract：A comprehensive fault diagnosis method was proposed for lubrication state of journal bearings based on empirical mode decomposition (EMD) and weighted grey relational degree, since a mapping relation exists between the energy distribution in different frequency bands of acoustic emission and the lubrication state. First, the acoustic emission signals were decomposed into a finite number of stationary intrinsic mode functions based on EMD algorithm, then false components contained in the IMF was eliminated using the correlation coefficient method, and finally the first 10-order IMF components containing main fault information were chosen to calculate the energy ratio and to construct the characteristic vector. Results show that the weighted grey relational analysis has good classification effect on recognition of small samples, which can be used to calculate the grey incidence of different acoustic emission signals, so as to perform fault diagnosis on lubrication state of journal bearings effectively.

Key words：journal bearing; fault diagnosis; empirical mode decomposition (EMD); energy ratio; weighted grey relational analysis; entropy-weight method

文章编号：1674-7607(2016)01-0042-06

中图分类号：TP133.3

文献标志码：A学科分类号：470.30

作者简介：卢绪祥(1972-)，男，河南信阳人，副教授，硕士生导师，主要从事动力机械振动控制、状态监测与故障诊断方面的研究．

基金项目：湖南省研究生科研创新资助项目(CX2014B382)；湖南省高校重点实验室开放基金资助项目(2011NGQ008)

收稿日期：2015-03-24

修订日期：2015-05-11

电话(Tel.):0731-85258408;E-mail:hncslxx@163.com.