基于弹塑性本构的RPV顶盖贯穿件焊缝安定性分析

高永建，　贺寅彪，　曹　明

(上海核工程研究设计院，上海 200233)



基于弹塑性本构的RPV顶盖贯穿件焊缝安定性分析

高永建，贺寅彪，曹明

(上海核工程研究设计院，上海 200233)

摘要：对CRDM贯穿件建立带J形焊缝的有限元分析模型，选取基于应力应变曲线的非线性随动强化Chaboche模型，依据ASME B&PVC-III-1-NB-3228.4的规定进行材料塑性条件下的安定性分析.结果表明：塑性安定性分析方法可以有效降低分析的保守性, 材料弹性假定下安定性无法保证的区域可以通过塑性安定性分析得以保证.

关键词：反应堆压力容器； CRDM贯穿件； J形焊缝； 安定性分析

近年来，基于失效模式的分析设计方法逐渐被工程界认可并推广应用，安定性失效作为结构的主要失效模式之一，也得到广泛重视和深入研究讨论[1-4].结构在给定范围的交变载荷作用下通常会出现2种情况：一种是在若干次循环载荷作用后，塑性交变趋于稳定，之后的结构响应是弹性的，即结构处于安定状态；另一种是在交变载荷作用下塑性变形不断累积或不断反复，最终导致结构破坏，其破坏形式分别对应于累积塑性破坏(或棘轮破坏)和交变塑性破坏(或低周疲劳破坏).

反应堆压力容器(Reactor Pressure Vessel, RPV)顶盖控制棒驱动机构(Control Rod Drive Mechanism, CRDM)管座J形焊缝属于承压边界焊缝，其失效将导致反应堆冷却器的泄漏及控制棒弹棒等事故的发生，因此根据ASME B&PVC-Ⅲ-Ⅰ-NB分卷的规定，有必要对该焊缝进行详细的应力分析与评定，保证其在设计寿命内的结构完整性.

J形焊缝应力评定通常包括一次应力强度评定、一次加二次应力强度评定和疲劳评定，由于该焊缝属于部分焊透焊缝，且位于结构不连续处，应力集中明显，分析发现一次加二次应力强度评定无法通过，依据ASME B&PVC-Ⅲ-Ⅰ-NB-3228.5[5]的规定，进行简化的弹塑性分析，发现扣除热弯曲应力后的一次加二次应力强度仍超过规范限值.为保证结构的安定性并最大限度地降低分析的保守性，应用有限元法，建立带J形焊缝的有限元分析模型，分别选取基于应力应变曲线的非线性随动强化Chaboche模型，依据ASME B&PVC-Ⅲ-Ⅰ-NB-3228.4的规定进行材料塑性条件下的安定性分析.由于应力分析与评定一般假定材料是弹性的，故材料塑性条件下的分析方法在工程界还鲜见研究报道，本文研究对应力集中较为明显的局部结构不连续区域的安定性分析具有重要借鉴意义.

1有限元模型

1.1几何结构和材料

反应堆压力容器的CRDM贯穿件位于压力容器顶盖处，共若干组，通过过盈胀接的方式与顶盖连接，其底部与顶盖之间设置J形焊缝，整体结构见图1，J形焊缝的结构示意图见图2.

压力容器顶盖材料为SA-508 Gr.3 Cl.1，其内壁堆焊厚度为6 mm的不锈钢，CRDM贯穿件和J形焊缝的材料为690镍基合金.上述各材料的热物理和力学性能参数及其随温度的变化见表1和表2[6].

图1　RPV顶盖和CRDM贯穿件几何结构

图2　J形焊缝结构示意图

性能温度/℃2050100150200250300350ν1)0.30.30.30.30.30.30.30.3Sm2)/MPa184184184184184184184184Sy3)/MPa345337326314305299292286Su4)/MPa552552552552552552552552E5)/MPa1.92×1051.90×1051.87×1051.84×1051.80×1051.77×1051.74×1051.72×105a6)/K-111.50×10-611.74×10-612.06×10-612.40×10-612.80×10-613.03×10-613.28×10-613.50×10-6λ7)/(W·m-1·K-1)40.7040.7440.5840.5040.0039.3138.5537.90D8)/(mm2·s-1)11.8311.4910.9210.359.769.318.838.41

注：1)泊松比；2)设计应力强度；3)屈服强度；4)抗拉强度；5)弹性模量；6)平均热膨胀系数；7)导热系数；8)热扩散系数.

表2　690镍基合金材料性能

1.2有限元分析方法

1.2.1有限元模型网格

对中心CRDM贯穿件和最外侧CRDM贯穿件进行分析评定，用以覆盖所有CRDM贯穿件.中心CRDM贯穿件有限元模型为轴对称模型(见图3)，单元类型根据分析类型(结构分析或热分析)及载荷类型(轴对称载荷或非轴对称载荷)的变化而变化：对压力瞬态和热瞬态的结构应力分析采用PLANE42二维结构实体单元；对机械载荷(轴力、剪力、弯矩和扭矩)作用下的结构应力分析采用可同时加载轴对称载荷和非轴对称载荷的PLANE25二维轴对称谐结构实体单元；对热分析采用PLANE55热实体单元.顶盖与贯穿件之间考虑接触分析，采用CONTA171二维接触单元和TARGE169二维目标单元，但对于非轴对称载荷加载下的分析，采用贯穿件与顶盖的对应节点在贯穿件径向做耦合来取代接触单元.

图3　中心CRDM贯穿件有限元模型

最外侧CRDM贯穿件采用60°范围内的三维有限元模型(见图4)，结构应力分析采用SOLID45结构实体单元，热分析采用SOLID70热实体单元，顶盖与贯穿件之间的接触采用CONTA173三维接触单元及TRAGE170三维目标单元.

图4　最外侧CRDM贯穿件有限元模型

1.2.2计算载荷

顶盖及CRDM贯穿件内壁将承受反应堆运行期间的所有压力和温度瞬态(按照ASME规范的要求，只需要考虑正常和异常工况下的瞬态，共计26个设计瞬态，限于篇幅，不详列)，并且CRDM贯穿件顶部异种金属焊缝和J形焊缝处还将承受由各种原因引起的交变机械载荷.

2塑性安定性分析

2.1问题描述

CRDM贯穿件及J形焊缝的应力评定路径见图5，通过材料弹性假定下的分析发现，J形焊缝处的一次加二次应力强度评定无法通过，依据ASME B&PVC-Ⅲ-Ⅰ-NB-3228.5的规定，做简化的弹塑性分析，结果发现：中心CRDM贯穿件的路径2内壁和路径4外壁与最外侧CRDM贯穿件的路径6内壁和路径10内壁，扣除热弯曲应力后的一次加二次应力强度仍超过规范限值.

(a)中心CRDM贯穿件(b)最外侧CRDM贯穿件

图5应力评定路径

Fig.5Stress evaluation paths

事实上，ASME规范基于应力分类的弹性分析方法是采用“虚拟弹性应力”的方法来考虑结构塑性问题的，从工程应用的角度来看，此方法确实方便实用，但也存在其固有的缺陷，例如当结构进入塑性状态后，应变迅速增加，因此由弹性模量乘以应变得到的“虚拟弹性应力”快速增加，对于局部结构不连续的高应力(应变)区，“虚拟弹性应力”会很大，因此，极有可能造成安定性评定无法通过，而实际上材料进入屈服后应力不会继续以弹性模量的斜率增大.为最大限度地降低弹性分析带来的保守性，依据ASME B&PVC-Ⅲ-Ⅰ-NB-3228.4的规定，进行材料塑性条件下的安定性分析.ASME B&PVC-Ⅲ-Ⅰ-NB-3228.4(b)规定：对规定的最小屈服强度与规定的最小抗拉强度之比小于0.70的材料，只要在其上任何一点由塑性分析所考虑的运行循环所造成的最大累积局部应变不超过5%，则无需满足安定性要求.

2.2基于实测拉伸性能的安定性分析

选取基于应力应变曲线的非线性随动强化Chaboche模型，依据ASME B&PVC-Ⅲ-Ⅰ-NB-3228.4的规定进行材料塑性条件下的安定性分析.316 ℃下690镍基合金的应力应变曲线见图6.选用Ansys有限元程序的非线性随动强化Chaboche模型，该模型适用于大应变和循环加载，可模拟单调强化和包辛格效应(Bauschinger effect)，可模拟非对称应力加载条件下的材料塑性棘轮(Ratcheting)效应和安定性(Shakedown)效应.利用式(1)所示的6参数Chaboche模型对图6所示的应力应变曲线进行拟合，得到各参数数值.

(1)

屈服强度Sy=190 MPa，C1=67 040，γ1=800，C2=2 458，γ2=25，C3=43 220，γ3=190.

图6　316 ℃下690镍基合金应力应变曲线

2.3分析方法与结果讨论

根据安定性原理，只要一次加二次应力强度范围不超过3Sm，则不会产生塑性应变的累积，因此为简化分析，将一次加二次应力强度范围超过3Sm的所有配对组合的循环次数相加，得到总循环次数N，将最大一次加二次应力强度范围对应的配对组合的2个瞬态做N次循环，如果评定点处的累积塑性应变小于5%，则认为该处满足安定性要求.

按上述分析方法，对贯穿件及J形焊缝的材料采用第2.2节所述的塑性本构模型，利用Ansys有限元程序进行塑性安定性分析，得到中心CRDM贯穿件路径4外壁的应力强度与塑性应变强度的关系，见图7.由图7可以看到表征塑性应变累积的滞回曲线，路径4外壁的累积塑性应变强度为0.845%，满足5%的限值.

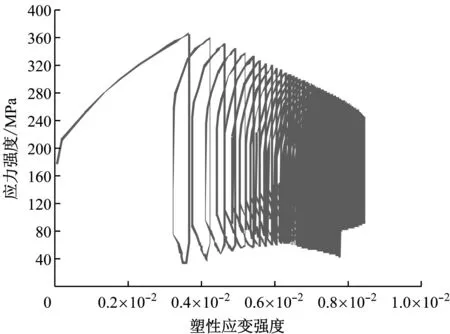
图7　应力强度与塑性应变强度的关系

3结论

塑性安定性分析可以有效降低弹性分析的保守性，材料弹性假定下安定性无法保证的区域可以通过塑性安定性分析得以保证，该分析方法对应力集中较为明显的局部结构不连续区域的安定性分析具有重要借鉴意义.

参考文献：

[1]徐栓强，俞茂宏. 拉压强度不同材料厚壁球壳的安定性分析[J]. 机械设计与制造，2005(1)：36-37.

XU Shuanqiang, YU Maohong. Shakedown analysis of thick spherical shell of material with different strength in tension and compression[J]. Machinery Design &Manufacture, 2005(1): 36-37.

[2]董龙梅，杨涛，孙显. 基于ANSYS对压力容器的应力分析与结构优化[J]. 机械设计与制造，2008(6)：99-100.

DONG Longmei, YANG Tao, SUN Xian. Stress analysis and structure optimization of pressure vessel on ANSYS[J]. Machinery Design &Manufacture, 2008(6): 99-100.

[3]郑小涛，轩福贞. 压力容器与管道安定/棘轮评估方法研究进展[J]. 压力容器，2013，30(1)：45-53.

ZHENG Xiaotao，XUAN Fuzhen. Advances in shakedown/ratcheting estimation methods for pressure vessels and piping[J]. Pressure Vessel Technology, 2013, 30(1)：45-53.

[4]王飞，栾茂田.安定荷载上限近似解的数值分析方法及其应用[J]. 工程力学，2003，20(5)：76-81.

WANG Fei, LUAN Maotian. Numerical procedures of upper-bound approximation of shakedown loads and its application in engineering[J]. Engineering Mechanics, 2003，20(5)：76-81.

[5]美国机械工程师学会. ASME锅炉及压力容器规范:第III卷第一册NB分卷[S]. 美国：美国机械工程师学会,1998.

[6]美国机械工程师学会. ASME锅炉及压力容器规范:第II卷材料性能篇[S]. 美国：美国机械工程师学会,1998.

Shakedown Analysis of the J-weld Between RPV Closure Head and

CRDM Penetration Based on Elastoplastic Constitutive ModelGAOYongjian,HEYinbiao,CAOMing

(Shanghai Nuclear Engineering Research and Design Institute, Shanghai 200233, China)

Abstract：Finite element models were set up for the J-weld between reactor pressure vessel (RPV) closure head and control rod drive mechanism (CRDM) penetration, and subsequently a shakedown analysis was conducted on the J-weld according to ASME B&PVC-III-1-NB-3228.4 using Chaboche nonlinear kinematic hardening model based on stress-strain curves. Results show that the plastic shakedown analysis could reduce the conservatism of analysis effectively, and the shakedown requirements that could not be satisfied under elastic material assumption could be alternatively guaranteed by the plastic shakedown analysis.

Key words：reactor pressure vessel (RPV); CRDM penetration; J-weld; shakedown analysis

文章编号：1674-7607(2016)01-0079-05

中图分类号：TL351

文献标志码：A学科分类号：490.50

作者简介：高永建(1983-)，男，浙江杭州人，工程师，硕士，主要从事反应堆结构力学分析方面的研究.电话(Tel.)：021-61863766;

基金项目：国家科技重大专项——大型先进压水堆核电站重大专项资助项目(2010ZX06002)

收稿日期：2015-06-17

修订日期：2015-07-10

E-mail: gaoyj@snerdi.com.cn.