圆锥曲线中定值问题的探讨

楚尔轩



圆锥曲线中定值问题的探讨

楚尔轩

在系统复习圆锥曲线这一内容时，我发现有许多问题都要求学生求出其定值。定值题变化多端，解法也很多。本文总结了一些常用的思路，对提高复习教学的效率也许会带来帮助。椭圆C=1（a＞b＞0）的左顶点A（-a，0），M，N两点在椭圆C上，且AM⊥AN。问：直线MN是否经过定点？若是，求出这个点的坐标；若不是，说明理由。

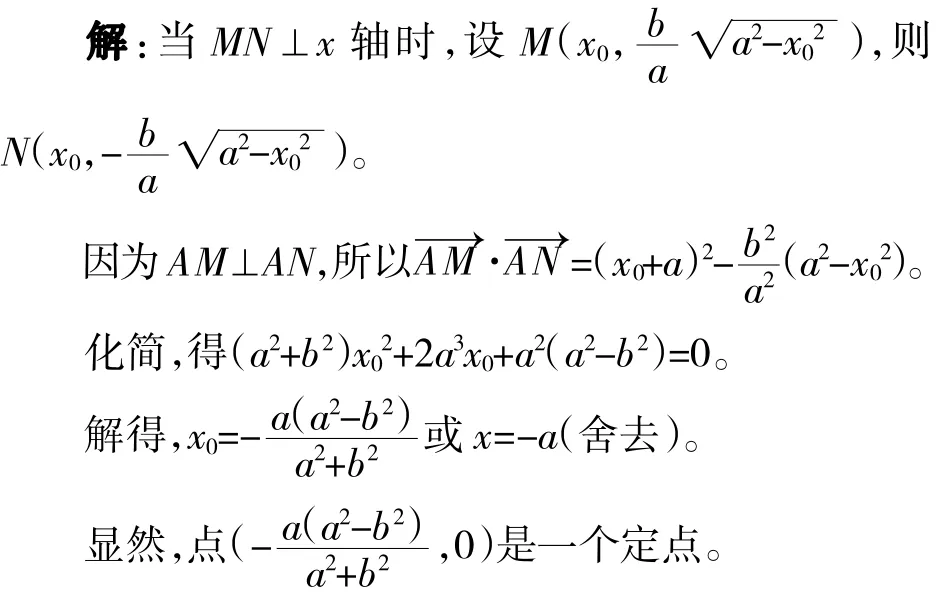
当MN不垂直x轴时，设直线MN的方程为：y= kx+m，则与椭圆C的方程联立组成方程组：

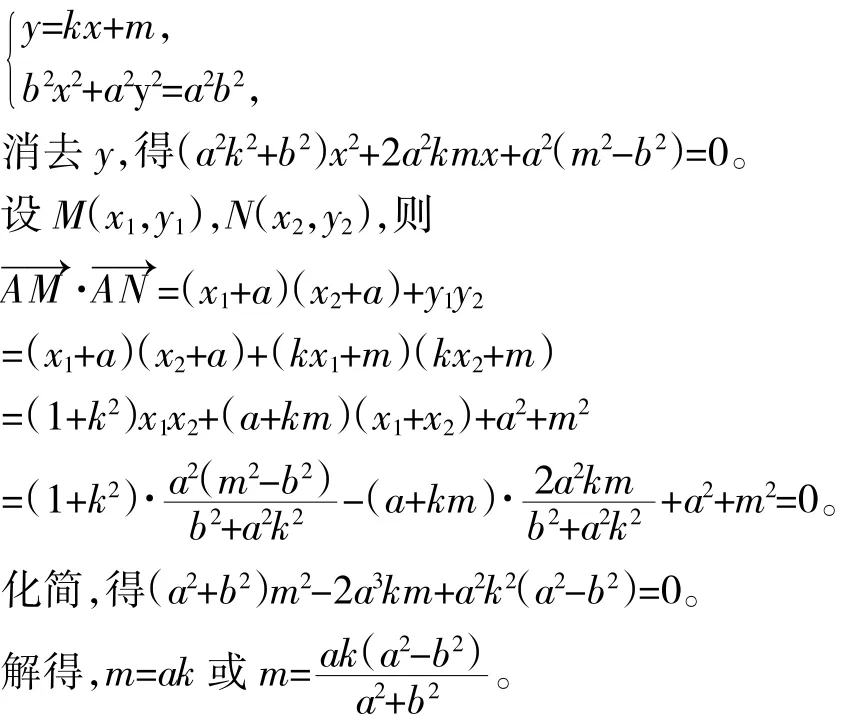
当m=ak时，直线MN：y=kx+ak，恒过定点（-a，0），不合题意，舍去。

当m= ak（a2-b2）

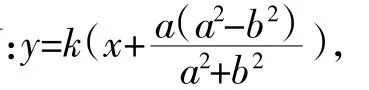
c2=2。

而a2=b2+2，故解得，a2=4，b2=2。

设点Q（x，y），A（x1，y1），B（x2，y2）。

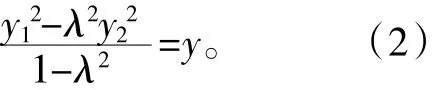
又点A，B在椭圆C上，所以

从（1）（2）（3）消去x1，x2，y1，y2，λ，得2x+y=2。这是定直线，故问题得证。

（作者单位：长沙市南雅中学）

湖南教育报刊社新版记者证情况公示

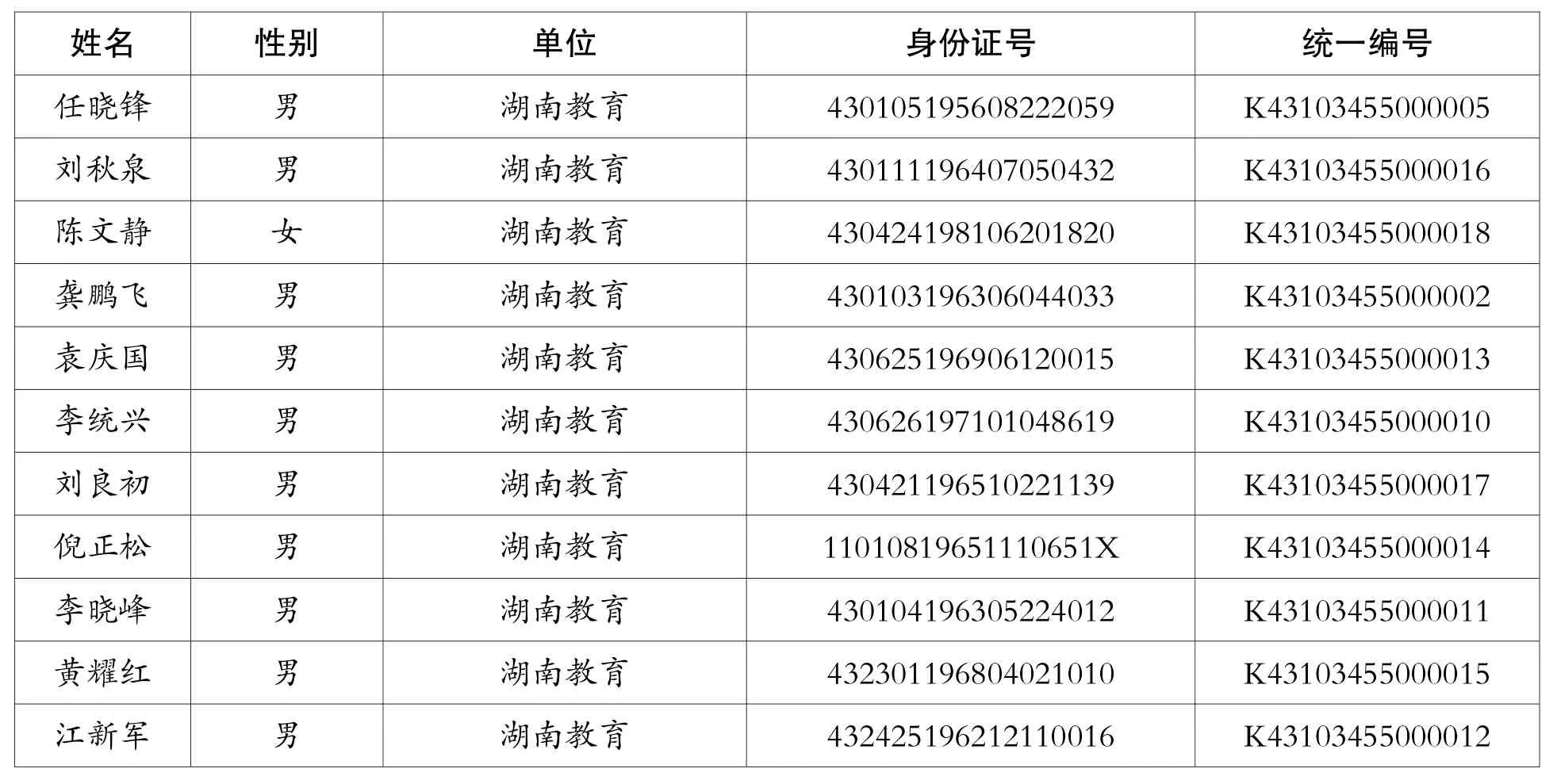
姓名　性别　单位　身份证号　统一编号任晓锋　男　湖南教育　430105195608222059　K43103455000005刘秋泉　男　湖南教育　430111196407050432　K43103455000016陈文静　女　湖南教育　430424198106201820　K43103455000018龚鹏飞　男　湖南教育　430103196306044033　K43103455000002袁庆国　男　湖南教育　430625196906120015　K43103455000013李统兴　男　湖南教育　430626197101048619　K43103455000010刘良初　男　湖南教育　430421196510221139　K43103455000017倪正松　男　湖南教育　11010819651110651X　K43103455000014李晓峰　男　湖南教育　430104196305224012　K43103455000011黄耀红　男　湖南教育　432301196804021010　K43103455000015江新军　男　湖南教育　432425196212110016　K43103455000012

湖南省新闻出版广电局举报电话：0731-84801373