一种基于多尺度和改进支持向量机的光纤陀螺温度漂移建模与补偿方法
王 威,陈熙源
(东南大学 仪器科学与工程学院,南京 210096)
一种基于多尺度和改进支持向量机的光纤陀螺温度漂移建模与补偿方法
王 威,陈熙源
(东南大学 仪器科学与工程学院,南京 210096)
为了提升光纤陀螺温度漂移模型建模的准确性及补偿的效果,提出了一种基于改进支持向量机的多尺度建模和回归方法。首先分析了造成光纤陀螺温度漂移的关键因素,给出了建模的属性参数和温度试验。然后根据经验模态分解得到的本征模态函数排列熵的变化趋势,得出了回归精度和熵之间的变化关系,进而提出了基于信号分解的多尺度回归方法。为了提高上述多尺度回归算法的适应性,在传统支持向量机的基础上,提出了基于组合核函数的支持向量机回归算法,以适应不同特性的回归数据集。为了进一步提高回归精度,基于降低回归数据复杂度的分段回归思想,在上述多尺度回归的基础上提出了双-多尺度回归,并验证了方法的有效性。最后,将提出的算法以实际的光纤陀螺温度漂移数据进行验证,结果表明,相比于传统的支持向量机和反向传播神经网络具有更好的回归精度,温度漂移模型也更加精确,以均方误差指标为例,回归精度提升了两个数量级。
经验模态分解;排列熵;多尺度;支持向量机
光纤陀螺是基于sagnac效应的光学仪器[1],具有可靠性高、启动时间短、动态范围大、体积小等优点,已经成为现代导航、测量系统中的主要器件。构成光纤陀螺的核心部件对温度较为敏感,当环境温度发生变化时,在陀螺的输出信号中将产生非互易性相位误差[2],导致光纤陀螺产生温度漂移。温度漂移是光纤陀螺的主要误差源,严重制约着光纤陀螺的精度,因此有必要采取补偿措施来消除这种误差。解决光纤陀螺温度漂移的方法主要有两种:一种是硬件补偿[3-4],这种补偿比较复杂,会造成成本和体积的增加;另一种是软件补偿,这种方法较为灵活,效果较好[5-6]。
近年来,随着人工智能算法的不断发展,光纤陀螺温度建模与补偿算法也得到了广泛的应用。人工神经网络算法是一种常见的智能算法,将其应用于光纤陀螺的建模与补偿,得到了较好的效果[7]。但人工神经网络较差的泛化能力,隐层节点数确定的经验化和精度较差等问题严重制约了其进一步的应用。小波也常被用于陀螺的温度建模[8],但对于小波基的选择与改进、小波阀值等的参数设定等没有明确的指导理论,影响了其使用的精度。支持向量机(SVM)具有比人工神经网络更好的泛化能力、更好的抗过拟合能力以及更好的回归能力。文献[9]把SVM应用到了陀螺的建模与补偿上,但由于回归数据的非线性和复杂性,传统的支持向量机回归精度还有较大提升空间。
本文对信号复杂度(熵)和回归精度的关系进行了仿真研究,为多尺度回归和建模打下基础。针对传统SVM回归能力的不足,从核函数着手,构造出同时适应高频和低频非线性信号的组合核函数,试验证明了其回归效果好于单一的核函数。为了进一步提高回归精度,本文从分段回归的思想出发,结合组合核函数的强适应性,提出了固定步长的分段回归方法。结合以上三项创新点,形成了基于双-多尺度的组合核函数支持向量机回归方法,本文最后的回归试验证明了新方法的有效性。
1 光纤陀螺仪的温度漂移
D. M. Shupe在他的文章[2]中指出,干涉式光纤陀螺仪会因为光纤环上的温度变化导致光纤折射率的变化,进而引起非互易性相移。这种相移是光纤陀螺输出误差的主要成分,会给光纤陀螺的造成不可忽视的漂移,从而影响其应用。电气和电子工程师协会(IEEE)在IEEE Std 952-1997标准里给出了光纤陀螺温度漂移模型公式,如式(1)所示:

图1中陀螺的输出频率为100 Hz,图中数据采用了10 s平滑处理,并已经减去了陀螺常值漂移(包括地球转速分量)。

图1 FOG温度漂移输出Fig.1 Output of FOG temperature drift
2 多尺度回归
信号的多尺度分解可以把信号中不同频率的分量提取出来,使信号的频谱进行分离,进而降低了信号的复杂度。EMD[10]、EEMD[11]、CEEMDAN[12]和掩膜信号EMD[13](简称M-EMD)是一类常见的信号时域分解方法,此类算法无需基函数和复杂的参数设定,能够在时域内逐层进行分解。以EMD为例,对上述±8 (°)/min的温漂数据进行分解,得到如图2所示的本征模态函数(IMF)序列波形。
由图2可见,从IMF1至IMF7,信号的复杂度程度逐渐降低,直至IMF7时接近于单调直线。以排列熵作为衡量信号复杂度的工具[14],图2中各个IMF的排列熵的值如图3所示。
由图3可见,随着IMF阶数的增加,信号的熵值(即信号的复杂度)呈现出类似线性化降低的趋势。此时,以支持向量机(SVM)作为回归工具,把第1节所述的建模参数作为SVM的属性矩阵的列向量,分别对上述IMF进行回归,得到回归误差MSE如图4所示。由图4可见,随着IMF阶数的增加,回归的误差迅速降低,回归的精度得到了大幅的提升。
为了比较多尺度和非多尺度的回归差别,同时比较不同信号分解方法的多尺度回归效果,分别对EMD、EEMD、M-EMD和CEEMDAN等方法对上述温漂数据进行多尺度回归,总的MSE如图5所示,为了便于查看,MSE的值扩大了10倍后显示于图中。

图2 FOG温度漂移EMD分解图Fig.2 EMD decomposition of FOG temperature drift

图3 IMF的排列熵Fig.3 Permutation entropy of intrinsic mode function

图4 SVM回归IMF的MSE误差Fig.4 Mean square error of SVM regression of intrinsic mode function
由图5可见,多尺度回归较非多尺度回归在精度上有较大提升,是一种简单、有效提升回归精度的方法,其中以 EMD分解后的多尺度回归效果最好。
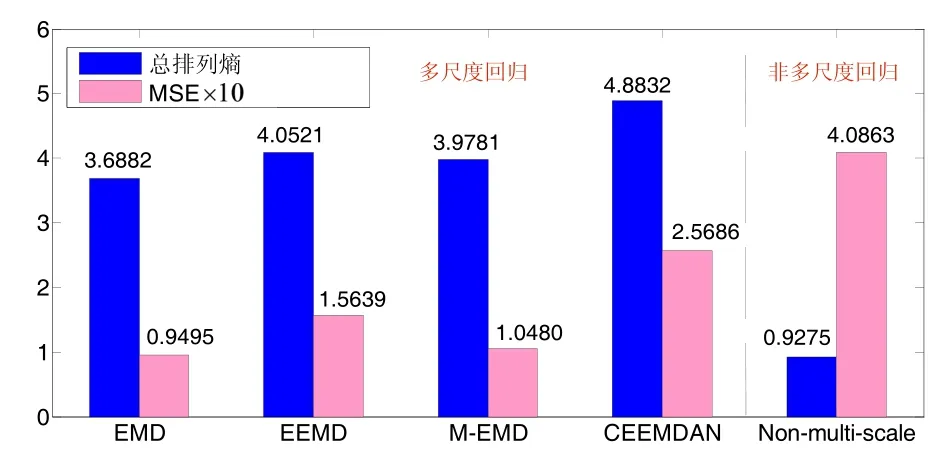
图5 不同回归算法的熵及MSE对比Fig.5 Comparison on entropies and MSEs by different regression algorithms
SVM是从基于超平面的线性分类器发展而来的,因其良好的泛化能力和分类精度而得到了广泛的应用。对于线性可分数据集(xi,yi),线性SVM分类器的输出是u=w·x-b,这里的w是超平面的权向量,SVM的目的就是计算出w和b。最大化margin(两个分类平面之间的距离)等价于求下面的二次优化问题,如式(2)和式(3)所示:

若数据集是线性不可分的,需要把它映射到更高维的特征空间,使其线性可分,这里的映射函数即为核函数。对于非线性分类器就要把x映射到特征空间,同时考虑误差ε的存在,上述优化问题变为

公式中的C为惩罚系数,ξi为松弛因子。其中C越大,回归效果越好,但其泛化能力越差。以 SVM对陀螺温漂进行建模,则其模型为

随着SVM的发展,核函数对分类、回归的性能影响越来越大,核函数已经成为SVM的研究热点。虽然核函数关系到分类、回归的性能,但至今还没有关于核函数选择及参数设定的系统化的理论支撑。组合核函数是基于博弈论提出的一种适应不同信号特点的新型核函数。有的核函数适合高频变化信号,即
3 基于组合核函数的支持向量机及陀螺温漂模型
核函数具有较强的局部描述能力,比如径向基核函数(RBKF);有的核函数适合对信号的整体描述,比如多项式核函数(PKF)。
上述两个核函数的定义如式(6)所示:

式中:d为多项式核函数的阶数,σ为核函数的宽度,σ越小,局部描述能力越强,若σ过小,则会带来过拟合和泛化能力下降的问题。对于非线性信号而言,其在不同时间上对于信号局部和整体描述能力的要求是不一样的,理论上来说,组合核函数能够更灵活、有效地对信号进行准确描述。根据核函数加法和乘法封闭的特点,同时为了兼顾核函数的局部性和整体性,本文构造的核函数如式(7)所示:

式中:ρ取值范围为[0,1],本文以0.1作为步长进行寻优;σ为RBKF的核宽度;d为多项式核函数的阶数。ρ的选取关系到组合核函数对信号整体性和局部性描述的权重问题,适当选择ρ可以提高信号的分类和回归精度。d选取越大,计算量越大,整体描述效果越差,为此,本文d选取1。公式中ρ和σ的最佳参数由传统的网格寻优方法即可获得[10],这里不再赘述。
对于结合多尺度回归方法和基于组合核函数的SVM方法,本文为了描述方便,称之为RBF-P-SVM方法。为了证明组合核函数的优势,对图1中的温漂数据分别采用本文的组合核函数及单一 RBF核函数进行回归,基于组合核函数的SVM回归误差MSE为0.0281,而基于RBF核函SVM的回归误差MSE为0.4086,优势明显。
4 分段回归
分段回归是一种降低信号复杂度,提高信号特征一致性的一种局部方法[15]。分段回归一般根据信号的局部特点进行人为地划分分段区间,这样势必会带来人为误差。鉴于引入了适应不同信号特征的组合核函数,本文将以固定步长作为分段回归窗口长度。为了验证算法的有效性,以原始±8 (°)/min的温漂数据作为回归对象,以固定步长30为分段回归窗口长度,在没有EMD等多尺度分解的情况下,SVM回归的误差曲线如图6所示。
图6中传统SVM回归的MSE为0.2079,分段回归的MSE为0.0147,由此可见,分段回归是一种简单却行之有效的提高回归精度的方法。结合多尺度回归方法、分段回归和组合核函数的SVM方法,本文称之为双-多尺度回归(简称RBF-P2-SVM)。
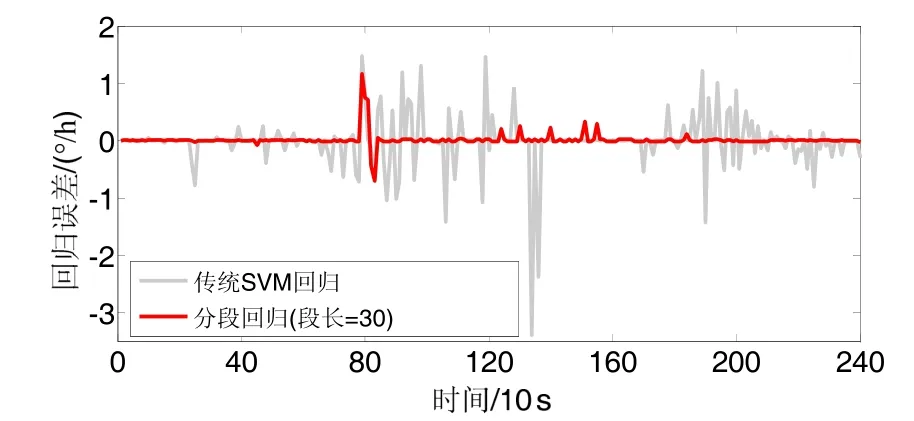
图6 分段回归与非分段回归的比较Fig.6 Comparison on piecewise regression and non-piecewise
5 实验验证
为了验证算法的有效性,分别应用上述的 RBFP2-SVM和RBF-P-SVM回归方法,同时结合EMD分解方法对±8 (°)/min的温漂数据进行建模、回归和补偿。在实际应用SVM或BP回归时,把不同温变速率实验下的温漂数据分别设置为测试集和验证集时得到的回归精度很差,为此,本文采用自回归对温漂数据进行建模、回归。为了寻找最优分段回归的窗口长度,设置递增步长为10进行多尺度回归寻优,在RBF-P2-SVM算法下,步长与回归误差MSE曲线如图7所示。由图7可知,最佳步长为80,此时回归误差MSE为0.0014。

图7 分段回归的段长选择Fig.7 Selection of piecewise regression length
为了验证算法的有效性,本文引入了BP神经网络回归作为比较方法,其中BP隐藏节点数设置为20。同时采用RBF-P-SVM和RBF-P2-SVM进行对比回归,回归、补偿后的数据如图8所示。由图8可见,BP神经网络回归效果最差,本文提出的RBF-P-SVM和RBF-P2-SVM具有更小的回归误差(两种方法均以EMD分解作为多尺度回归对象),其中双-多尺度回归方法RBF-P2-SVM精度最高。
以均方误差(Mean Squared Error,MSE)和误差平方和(sum of the squared errors,SSE)作为衡量回归精度的指标,分别对上述回归误差进行计算,结果如表1所示。由表1可见,RBF-P2-SVM较传统SVM回归和BP神经网络回归的精度提升了两个数量级以上,回归效果理想。

图8 回归误差的比较Fig.8 Comparison on regression errors

表1 回归误差比较Tab.1 Comparison on regression data
6 结束语
本文首先分析了回归精度和信号熵之间的变化关系,据此提出了多尺度回归算法。针对传统SVM核函数单一、适应性不强的问题,根据核函数的运算规律,提出了适用范围更广的组合核函数。为了进一步提高回归精度,本文引入了分段回归的算法,该算法摒弃了传统的人为分段的不足,在组合核函数的支撑下以固定步长进行分段回归。本文最后以实际的数据对上述双-多尺度和组合核函数的SVM方法进行了验证,结果表明,该方法的回归精度具有明显的优势,以MSE为例,回归精度较传统SVM和BP提升了两个数量级。
(References):
[1] Nayak J. Fiber-optic gyroscope: from design to production[J]. Appl. Opt, 2011, 50: E152–E161.
[2] Shupe D M. Thermally induced nonreciprocity in the fiber-optic interferometer[J]. Appl Opt, 1980, 19: 654-655.
[3] Xu H J, Zhang W Y, Xu X B, et al. Song. Research on thermal induced non-reciprocity in fiber-optic gyroscope with double optical length[J]. Acta Photonica Sinica, 2014, 43(10): 100600.1-100600.5.
[4] Wang X Y, He C C, Wang Z Y. Method for suppressing the bias drift of interferometric all-fiber optic gyroscopes[J]. OPT LETT, 2011, 36(7): 1191-1193.
[5] Chen X Y, Shen C. Study on temperature error processing technique for fiber optic gyroscope[J]. Optik, 2013, 124(9): 784-792.
[6] Song R, Chen X Y, Shen C, et al. Zhang. Modeling FOG drift using back-propagation neural network optimized by artificial fish swarm algorithm[J]. Journal of Sensors, 2014: 1-6.
[7] Feng Z, Xu J G, Li J S, et al. IUKF neural network modeling for FOG temperature drift [J]. Journal of Systems Engineering and Electronics, 2013, 24(5): 838-844.
[8] Zhang Q, Wang L, Gao P, et al. An innovative wavelet threshold denoising method for environmental drift of fiber optic gyro[J]. Math. Probl. Eng., 2016, Article No. 9017481.
[9] Q. Zhang, L. Wang, P. Gao, and Z. Liu. An Innovative Wavelet Threshold Denoising Method for Environmental Drift of Fiber Optic Gyro [J]. MATH PROBL ENG, 2016, Article Number: 9017481
[10] 程骏超, 房建成, 吴伟仁, 等. 基于SVM的激光陀螺温度误差建模与补偿方法[J]. 仪器仪表学报, 2013, 04: 721-727. Cheng J C, Fang J C, Wu W R, et al. Modeling and compensation method for temperature error of laser gyroscope based on support vector machine[J]. Chinese Journal of Scientific Instrument, 2013, 34(4): 721-727.
[11] Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for non-linear and non-stationary time series analysis[C]//Proceedings of the Royal Society of London A. 1998, 454: 903-995.
[12] Zhao Z D, Yang L, Chen D D, et al. A human ECG identification system based on ensemble empirical mode decomposition[J]. Sensors, 2013, 13(5): 6832-6864.
[13] Torres M E, Colominas M A, Schlotthauer G, et al. A complete ensemble empirical mode decomposition with adaptive noise[C]//IEEE Int. Conf. on Acoust., Speech and Signal. 2011: 4144-4147.
[14] Deering R, Kaiser G. The use of a masking signal to improve Empirical Mode Decomposition[C]//Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing. 2005, IV: 485-488.
[15] 冯辅周, 饶国强, 司爱威, 等. 排列熵算法的应用与发展[J]. 装甲兵工程学院学报, 2012(2): 34-38. Feng Fu-zhou, Rao Guo-qian, Si Ai-wei, et al. Application and development of permutation entropy algorithm[J]. Journal of Academy of Armored Force Engineering, 2012(2): 34-38.
[16] 冯卡力, 李安, 覃方君. 基于多模型分段拟合的光纤陀螺温度误差补偿方法[J]. 中国惯性技术学报, 2014, 22(6): 825-828. Feng Ka-li, Li An, Qin Fang-jun. Temperature error compensation method for FOG based on multi-model piecewise fitting[J]. Journal of Chinese Inertial Technology, 2014, 22(6): 825-828.
Modeling and compensation method of FOG temperature drift based on multi-scale and improved support vector machine
WANG Wei, CHEN Xi-yuan
(School of Instrument Science and Engineering, Southeast University, Nanjing 210096, China)
A multi-scale modeling and regression method is proposed based on an improved support vector machine to improve the accuracy and the compensation effect of FOG (fiber optic gyroscope) temperature drift model. Firstly, the factors that cause the FOG temperature drift are analyzed, and the attribute parameters and the temperature test are given. According to the change trend of IMF (intrinsic mode function) permutation entropy obtained by empirical mode decomposition, the relationship between the regression accuracy and the entropy is given, and a multi-scale regression method based on signal decomposition is proposed. In order to improve the adaptability of multi-scale regression algorithm to different characteristics of the regression data sets, a new support vector machine (SVM) algorithm based on combined kernel function (CKF) is proposed from traditional SVM. In order to further improve the regression accuracy, a two- and multi-scale regression method is proposed by using piecewise regression to reduce the complexity of regression data, and the effectiveness of this method is verified by the test results. Finally, this two- and multi-scale CKF SVM regression algorithm is verified by simulation using actual temperature drift data of FOG, which shows that the regression accuracy is better than those of traditional SVM and BP neural network, and the temperature drift model is more accurate. Taking the MSE index as an example, the regression precision has been improved by two orders of magnitude.
empirical mode decomposition; permutation entropy; multi-scale; support vector machine
U666.1
:A
2016-08-08;
:2016-11-20
国家自然科学基金(51375087,50975049)
王威(1979—),男,博士研究生,从事惯性导航研究。E-mail: 230159566@seu.edu.cn
联 系 人:陈熙源(1962—),男,教授,博士生导师。E-mail: chxiyuan@seu.edu.cn
1005-6734(2016)06-0793-05
10.13695/j.cnki.12-1222/o3.2016.06.017

