卫星分群的抗差Kalman滤波在GPS/BDS融合精密单点定位中的应用
王 琰,张传定,胡小工,宋叶志,马绍龙,唐成盼,李 冉
(1. 解放军信息工程大学 地理空间信息学院,郑州 450052;2. 北京卫星导航中心,北京 100094;3. 中科院上海天文台,上海 200030;4. 南京陆军指挥学院 军队指挥系,南京 210045)
卫星分群的抗差Kalman滤波在GPS/BDS融合精密单点定位中的应用
王 琰1,2,张传定2,胡小工3,宋叶志3,马绍龙4,唐成盼3,李 冉3
(1. 解放军信息工程大学 地理空间信息学院,郑州 450052;2. 北京卫星导航中心,北京 100094;3. 中科院上海天文台,上海 200030;4. 南京陆军指挥学院 军队指挥系,南京 210045)
抗差Kalman滤波是控制GNSS动态导航定位中观测异常的有效算法,当应用到GPS/BDS实时动态精密单点定位(Precise Point Positioning, PPP)时,会出现某些历元定位精度甚至不如单一系统定位精度高,这主要是因为同一接收机接收的不同种类卫星观测量的随机特性不同,使得观测量验后残差的分布特性不一致,抗差估计时随机特性不同的观测量验后残差互比,反而对某一系统优质数据也进行了降权,导致定位结果出现偏差,减弱了 GPS/BDS融合精密单点定位的优势。针对这一问题,提出了卫星分群的抗差Kalman滤波算法,并应用到GPS/BDS融合精密单点定位中,算法的核心是在每一历元观测数据质量控制时根据卫星类型分类构建方差膨胀因子,给出了算法的实施步骤,最后通过MGEX实测数据进行了验证,结果表明算法应用到GPS/BDS融合精密单点定位中,相较传统的抗差Kalman滤波算法在东、北、天三个方向分别提高了34.6%、33.3%、31.0%,同时表明该算法提高了GPS/BDS融合精密单点定位的可靠性。
抗差估计;Kalman滤波;卫星分类定权;GPS/BDS;精密单点定位
精密单点定位(Precise Point Positioning,PPP)技术利用卫星精密星历和钟差产品获得全球任一接收机在ITRF下的绝对坐标,该技术经过了15年的发展,应用前景广阔[1]。北斗卫星导航系统(BeiDou Navigation Satellite System,BDS)是我国独立自主发展的导航系统,目前已经为亚太地区提供导航定位服务[2],GPS/BDS融合PPP吸引了一系列专家学者的广泛关注,相较单一导航系统的PPP解,GPS/BDS融合PPP增加了观测冗余,改善了定位的DOP值,能够提高PPP的精度和可靠性,缩短初始化时间,其优势毋庸置疑[2-7]。文献[2~7]研究了多系统融合PPP的函数模型,并采用实测数据评估了多系统融合PPP的定位精度与收敛时间,阐述了多系统融合 PPP的优势;文献[4][5]对GPS/BDS PPP的定位精度与收敛时间进行了比较。PPP技术还有许多关键算法需要改进,文献[8]对影响PPP定位的关键因素进行了分析研究。
众所周知,GNSS实时数据质量控制是保证动态导航定位精度的关键,对于GPS/BDS融合动态PPP,要尽量利用可以利用的观测数据,但要保证参与PPP解算的观测数据的质量,若质量较差的观测数据参与平差,非但无法起到增加观测冗余的作用,反而影响定位精度[9]。实时PPP随着历元向前处理,过程不可逆,因此无法像事后PPP根据前后历元观测量时间序列特性进行质量控制,故实时PPP质量控制更为重要[10]。
Kalman滤波在动态数据处理中应用较广,实时PPP一般也采用Kalman滤波,但是标准Kalman滤波无法对数据中的粗差进行有效处理。为了控制Kalman滤波递推过程中的观测异常,有两种思路:一种是文献[11]提出的与Kalman滤波并行操作的误差探测、诊断与修复的DIA(Detection, Identification, Adaptation)方法,该算法的理论基础是将粗差归于均值漂移的粗差探测技术;另一种是将抗差估计与 Kalman滤波相结合的抗差Kalman滤波,抗差Kalman滤波的理论基础是基于将粗差归于方差膨胀的稳健估计技术,不同于DIA算法对“值得怀疑”的异常数据进行硬性拒绝,抗差Kalman滤波通过对观测数据“降权”、“保权”、“拒绝”三种方式尽量利用可以利用的观测数据,从而保证定位结果的精度和可靠性,因此在GNSS动态数据处理中应用较广,其中以杨元喜等提出的抗差自适应滤波理论最具代表,该算法能能够更有效地控制异常影响,提高动态滤波精度,相关研究很多不再详述[12-13]。
抗差Kalman滤波在PPP中广泛应用,文献[9][10]对实时PPP的质量控制进行了详细研究,文献[13]提出了一种改进的抗差Kalman滤波方法并应用到精密单点定位中。对抗差估计的原理进行研究发现,抗差估计实际是根据参与平差的观测量验后残差进行互比,对验后残差离群的观测量进行降权,这个前提是参与定位的观测量验后残差向量同类、同分布。GPS/BDS融合PPP与基线解的模式不同,卫星星历误差无法通过差分消除或减弱,IGS提供的GPS卫星精密星历和钟差精度较高,而BDS采用了混合星座,不同种类的卫星星历精度存在偏差,同时轨道高度不同,外加测量噪声本身随机特性的不同,都造成GPS/BDS融合PPP观测量验后残差很难做到同类、同分布,因此本文提出了一种卫星分群的抗差Kalman滤波算法,并应用到GPS/BDS融合PPP中,介绍了算法的实施流程,最后采用MGEX实测数据验证了算法的有效性。
1 多系统融合PPP
1.1 GPS/BDS融合PPP的观测方程
GPS/BDS融合PPP示意图如图 1。PPP一般采用消电离层组合伪距和载波相位观测值,消去电离层一阶项误差。卫星轨道和钟差固定(一般采用IGS分析中心提供的精密星历和钟差产品),卫星钟差产品中包含了卫星端的伪距硬件延迟,接收机端的伪距硬件延迟被接收机钟差吸收。GPS/BDS融合PPP中GPS的观测方程如式(1)[1,3-4]:

式中:伪距和相位硬件延迟与模糊度参数无法分离,这也是PPP中模糊度无法固定的原因。PPP中模糊度参数一般采用浮点解:

前述表明接收机钟差参数会吸收接收机端的伪距硬件延迟,而此延迟与信号频率和导航系统相关,因此两个系统在接收机端会产生伪距硬件延迟之差,也即码偏差(Differenced Code Bias,DCB),另外由于不同导航系统时间基准有差异,因而在 GPS/BDS融合PPP时,同一个接收机对不同的导航系统观测方程中会采用不同的接收机钟差参数。融合PPP的观测方程一般以GPS系统的接收机钟差作为基准,其他系统的观测方程中增加ISB参数,该参数吸收了DCB和时间基准的系统偏差[3-5]。因此 GPS/BDS融合 PPP中BDS的观测方程为

图1 GPS/BDS融合PPP示意图Fig.1 Schematic of combining GPS/BDS with PPP
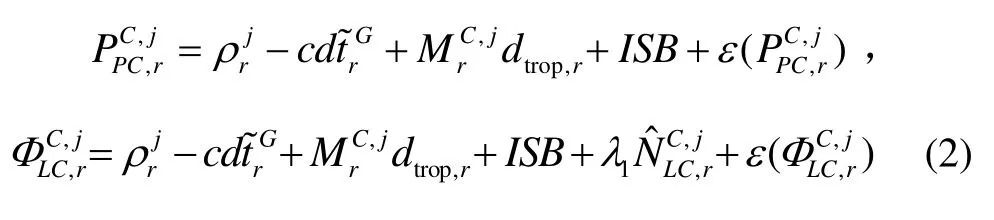
1.2 扩展Kalman滤波(EKF)

GPS/BDS融合PPP相较单一导航系统PPP具有很大的优势,但是作者在实际处理时发现,当某一系统的观测数据出现异常,若处理不当可能导致融合PPP的定位精度甚至不如单一导航系统的定位精度高。下面采用实测数据的算例进行说明。
1.3 试验分析
为了避免 EKF中由于载体运动导致状态参数出现异常的情况,采用静态仿动态的数据处理模式,以MGEX(Multi-GNSS Experiment)两个静态监测站GMSD和JFNG站2014年年积日070天的数据进行说明,GMSD和JFNG站分别位于日本和中国,两站接收GPS/BDS卫星情况如图 2所示,采用GFZ和WHU提供的星历产品进行PPP解算[14-15],比较以下三种方案的定位结果:方案1:单GPS PPP,采用IGS精密星历和30 s采样率的精密钟差产品;方案2:GPS/BDS融合 PPP,采用 GFZ提供的星历产品;方案 3:GPS/BDS融合PPP,采用WHU提供的星历产品。
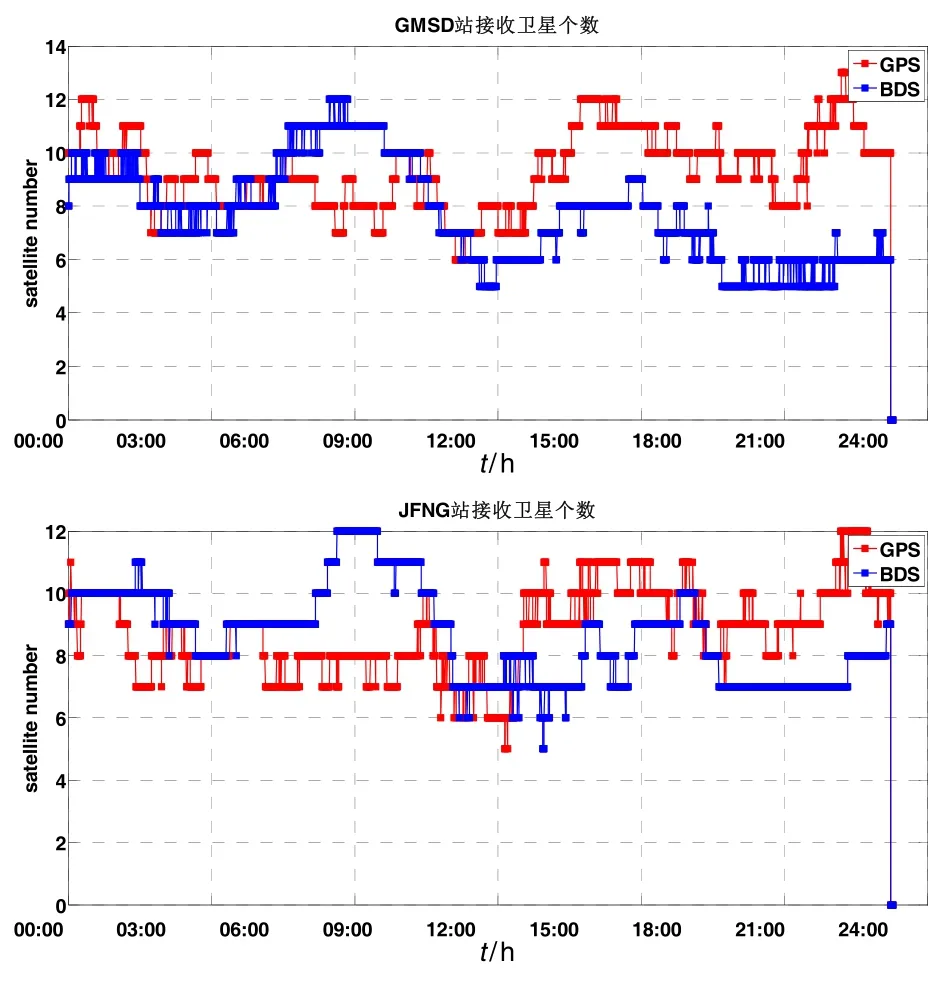
图2 可观测卫星数Fig.2 Number of visible satellites
三种方案解算策略一致,仅仅是采用的星历产品不同,对模糊度收敛后的定位结果进行统计,图 3、图 4分别为GMSD与JFNG站为三种方案每天50 min之后的PPP定位结果时间序列。
从图3和图4的结果可以看出:
1)GMSD站的定位结果说明GPS/BDS融合PPP能够提高定位精度,方案2、方案3定位结果的时间序列比方案1更加稳定,不会出现方案1中红色点迹的“毛刺”现象。同时图4中JFNG站方案1的定位序列在19:00-21:00天方向的定位结果较差,而同时期方案3的定位结果无异常,这是因为该段时间GPS观测数据存在异常值,BDS观测数据的加入弥补了这一不足,充分说明了GPS/BDS融合PPP的优势。

图3 GMSD站三种方案定位结果Fig.3 Positioning results of three schemes (site GMSD)
2)图 4中JFNG站方案1的定位序列在 12:00前后无明显异常,说明GPS观测量无明显异常,但是方案3的定位结果序列在这个时间段明显异常,分析是 BDS的观测数据存在异常造成了 GPS/BDS融合PPP定位结果在该时间段变差。

图4 JFNG站三种方案定位结果Fig.4 Positioning results of three schemes (site JFNG)
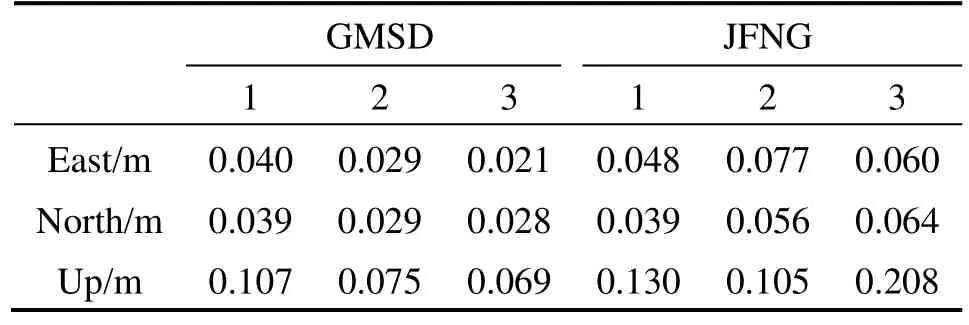
表1 GMSD与JFNG站三种方案的定位结果(RMS)Tab.1 Positioning results (RMS) of three schemes (site GMSD and JFNG)
3)图 4中JFNG站方案2在15:00-21:00时段内东方向的定位精度比方案3的要差,分析是由于该段时间GFZ提供的BDS轨道和钟差的精度不高,PPP数据处理模式与基线解不同,卫星端的星历误差无法通过差分消除,导致GPS/BDS融合PPP的定位精度甚至不如单 GPS系统的好。对于这一问题可以采用Helmert方差分量估计解决,拟在其他文章中另行介绍,本文不做讨论。
本文主要对前2个问题进行讨论。当两大系统每个历元的观测数据都存在冗余且均无异常观测量时,BDS/GPS融合PPP的定位精度明显要优于单GPS的定位精度。但是当其中一个系统的观测数据出现异常(星历精度的问题或者观测量本身的问题),导致另一系统的观测数据残差整体变大,使定位结果出现偏差,甚至不如单一导航系统的定位精度。
根据Helmert方差分量估计的思想,利用观测量的验后残差计算不同种类观测值的方差因子,从而对哪一类观测量出现了异常进行定位。式(6)为近似Helmert方差分量估计的Forstner公式,其中为第i类观测量的方差分量估计值,ni为当前历元该类观测量个数。按照文献[12][13]的研究,历史的观测异常误差会对Kalman滤波结果造成影响,从而影响对当前历元方差分量估计值的计算,故本文选取当前历元的观测量验后残差构建方差因子。若某一类观测在某一历元的方差分量估计值变大,说明当前历元此类观测值中存在异常。将GPS/BDS融合PPP的卫星按照类型分为四类:GPS、BDS GEO、BDS IGSO、BDS MEO。图5为JFNG站方案3中四类卫星的时间序列。


图5 JFNG站第i类观测量方差分量估计值的时间序列Fig.5 Variance-component estimation valueof type-i observables in site JFNG
图5中10:00至14:00之间GPS、GEO、IGSO三类卫星观测量的值均变大,前边分析了是由于BDS的观测量存在异常,GPS观测量的验后残差也相应变大,分别对JFNG站GPS/BDS的观测量验后残差做分析。图 6为JFNG站10:00-15:00之间GPS/BDS观测量验后残差序列:上图为GPS的结果,在12:00与14:00前后存在观测量残差出现离群的现象,但是不明显;下图为BDS的结果,明显地在11~12 h期间C01/C04星观测量出现异常,基于前后历元时间序列进行粗差探测,判定是 C01星观测量出现了异常,导致图 5中12:00左右BDS GEO卫星的方差分量估计值出现异常,相同历元的观测量验后残差均出现离群状态(GPS以及C04星的结果可以说明)。

图6 JFNG站10:00-15:00之间GPS/BDS观测量残差Fig.6 Post-fit phase residuals of GPS/BDS (time 10:00-15:00, site JFNG)
综上,对于GPS/BDS融合PPP,要避免观测数据中上述的异常才能发挥融合PPP的优势,抗差Kalman滤波是一种有效手段,但是若按照常规抗差 Kalman滤波计算等价权时,图 5中12:00前后GPS观测量验后残差也变大,C01观测量在降权的同时GPS卫星的观测量也整体降权,这就更造成了定位的偏差。因此本文提出了卫星分群的抗差 Kalman滤波算法来解决该问题,下面对算法进行介绍。
2 卫星分群抗差Kalman滤波
2.1 抗差Kalman滤波
抗差M-LS滤波极值条件[12]:

比较式(4)(8)两者的差异仅仅是在测量噪声的方差协方差矩阵由Qk变为了等价方差协方差矩阵,从而引起滤波增益矩阵Kk发生变化。鉴于 GPS/BDS融合PPP所有观测量是不相关的,将Qk对角线上第i个元素Qki乘以方差膨胀因子,就置换为。方差膨胀因子函数如式(9),该式利用IGG III权因子函数的倒数构建[12-13]。
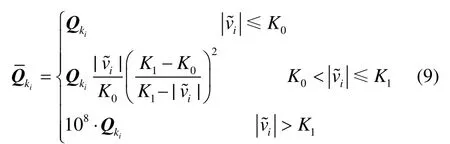
式中:K0、K1根据经验选取,在本文计算中,K0=1.5,K1=3.0;vi是当前历元某一相位观测量的验后残差,通过当前历元观测残差向量序列v=(v1,v2,…,vk)将当前vi化成标准化观测残差,的构建有多种方式,本文选取式(10)[13],其中σv是v的中误差。

2.2 卫星分群方差膨胀因子
前述分析知,GPS/BDS融合PPP中不同种类卫星的观测量验后残差序列v的随机特性不同,将当前历元观测残差向量序列v按照卫星类型分为四类v=(vG,vCG,vCI,vCM),G代表GPS卫星,CG代表BDS中GEO卫星,CI代表BDS中IGSO卫星,CM代表BDS中MEO卫星,不同类型卫星的观测量验后残差计算等价权因子如式(11):
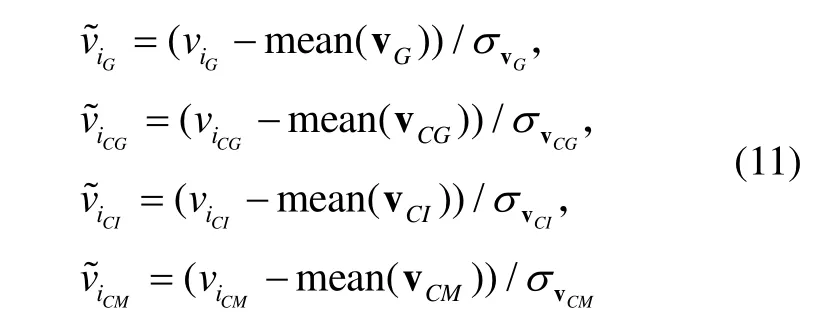
式中:σvG、σvCG、σvCI、σvCM为各类卫星观测量验后残差的中误差。每次抗差迭代时仅对该群观测量中验后残差最大的观测量进行方差膨胀,降低其对参数估计的贡献[13]。
3 试验分析
为了检验本文算法应用到GPS/BDS融合PPP中是否有效,收集了GMSD与JFNG站2014年年积日070-076共7天的数据进行试验分析,设计了三种方案:
方案1:标准Kalman滤波,采用最简单的3σ准则剔除每一历元的粗差数据。
方案2:常规的抗差Kalman滤波。
方案 3:采用本文提出的卫星分群抗差 Kalman滤波。
其中,GPS/BDS卫星精密星历和精密钟差选用WHU提供的产品。三种方案除每个历元数据质量控制模块不同外,其余数据处理策略均相同,从定位精度与可靠性两个方面评估本文算法的有效性。
3.1 定位精度
统计每天模糊度收敛后(每天50 min后)定位序列的RMS(结果如图 7),三种方案7天定位序列RMS的平均值如表 2所示。
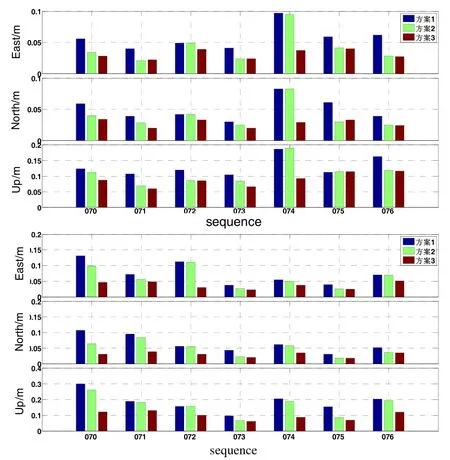
图 7 三种方案定位序列的RMS(上图为GMSD站,下图为JFNG站)Fig.7 Positioning results RMS of three schemes (The top one is the result of site GMSD, and the bottom one is the result of site JFNG)

表 2 三种方案定位序列RMS的平均值Tab.2 Mean values of positioning results by the three schemes
从图 7两个站多天的定位结果可以看出,方案3的定位结果最优,方案2次之,方案1的结果最差。表 2的统计结果显示本文算法相较传统的抗差Kalman滤波算法平均在东方向提高了34.6%,北方向提高了33.3%,天方向提高了31.0%。
3.2 可靠性
统计三种方案出现 GPS/BDS融合解比 GPS或BDS单独定位精度差情况的概率,作为衡量三种算法可靠性的一个重要指标。可靠性比较的方法:对每天模糊度收敛后的定位序列进行统计(每天50 min,7天共19 460个历元),统计所有历元中三种方案定位结果比GPS或者BDS单独定位精度差的百分比,若方案有效,则出现定位下降的百分比较小,结果如图 8所示。图 9为方案3这7天定位序列与GPS、BDS单独定位的时间序列。
采用本文提出的卫星分群的抗差 Kalman滤波算法,与传统的Kalman滤波法相比,GPS/BDS融合PPP定位结果的可靠性增强,出现融合解的结果比单独解的结果差的概率变小,但是仍存在某些历元出现GPS/BDS融合PPP的结果比单GPS、BDS的结果差的情况。
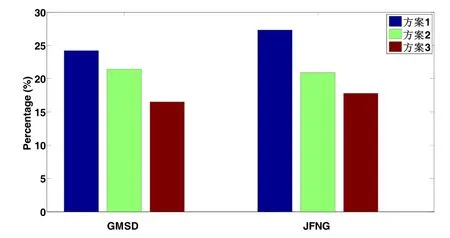
图8 三种方案可靠性比较Fig.8 Reliability comparison among three schemes

图9 GMSD站三种模式的定位序列Fig.9 Positioning sequence of the three schemes (site GMSD)
4 结 论
传统的抗差Kalman滤波算法在 GPS/BDS融合PPP数据处理中应用会存在些许不足:实时质量控制时因为不同随机特性的观测量互比,可能导致优质观测量过分降权的问题,导致定位结果甚至不如单一导航系统的定位精度高。本文采用MGEX实测数据对该问题进行了分析说明,并提出了改进的卫星分群抗差Kalman滤波算法。
算法的基本原理是根据卫星种类分群构建方差膨胀因子,避免同一接收机不同种类卫星的观测量互比,造成其中某一系统的正常观测量过分降权。本文给出了算法的实施步骤,最后采用MGEX实测数据检验了算法的有效性。与传统的抗差Kalman滤波算法相比,本文算法对GPS/BDS融合PPP的定位精度有一定提高,并且提高了GPS/BDS融合PPP的可靠性。
(References):
[1] Zumberge J, Heflin M, Jefferson D, Watkins M, et al. Precise point positioning for the efficient and robust analysis of GPS data from large networks[J]. Journal of Geophysical Research, 1997, 102 (B3): 5005-5017.
[2] 杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1-6. Yang Yuan-xi. Progress, contribution and challenge of compass/BeiDou satellite navigation system[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1-6.
[3] Cai C, Gao Y. Modeling and assessment of combined GPS/GLONASS precise point positioning[J]. GPS Solut, 2013, 17(2): 223-236.
[4] Zhang X, Li X. Instantaneous re-initialization in real-time kinematic PPP with cycle slip fixing[J]. GPS Solutions, 2012, 16(3): 315-327.
[5] Li X, Ge M, Dai X, et al. Accuracy and reliability of multi-GNSS real-time precise positioning: GPS, GLONASS, BeiDou, and Galileo[J]. J Geod, 2015, 89(6): 607-635.
[6] 米洋, 陈家斌, 刘红光, 等. 一种采用小波神经网络的GPS精密单点定位方法[J]. 中国惯性技术学报, 2016, 24(3): 337-341. Mi Yang, Chen Jia-bin, Liu Hong-guang, et al. GPS precise point positioning method using wavelet neural network[J]. Journal of Chinese Inertial Technology, 2016, 24(3): 337-341.
[7] 刘帅, 孙付平, 李海峰, 等. 前后向平滑算法在精密单点定位/INS紧组合数据后处理中的应用[J]. 中国惯性技术学报, 2015, 23(1): 85-91. Liu Shuai, Sun Fu-ping, Li Hai-feng, et al. Forwardbackward-smoothing algorithm with application to tightly coupled PPP/INS data post-processing[J]. Journal of Chinese Inertial Technology, 2015, 23(1): 85-91.
[8] Seepersad G, Bisnath S. Challenges in assessing PPP performance[J]. Journal of Applied Geodesy, 2014; 8(3): 205-222.
[9] 蔡华, 赵齐乐, 孙汉荣, 等. GNSS实时数据质量控制[J]. 武汉大学学报信息科学版, 2011, 36(7): 820-824. Cai Hua, Zhao Qi-le, Sun Han-rong, et al. GNSS real-time quality control[J]. Geomatics and Information Science of Wuhan University, 2015, 36(7): 820-824.
[10] 张小红, 郭斐, 李盼, 等.GNSS精密单点定位中的实时质量控制[J]. 武汉大学学报(信息科学版), 2012, 37(8): 940-944. Zhang Xiao-hong, Guo Fei, Li Pan, et al. Real-time quality control procedure for GNSS precise point positioning[J]. Geomatics and Information Science of Wuhan University, 2012, 37(8): 940-944.
[11] Teunissen P J G. Quality control in navigation systems[J]. IEEE Aerospace and Electronic System Magazine, 1990, 5(7): 35-41.
[12] Yang Yuan-xi. Robust Bayesian estimation [J]. Bulletine Geodesique, 1991, 65: 145-150.
[13] 张小红, 潘宇明, 左翔, 等. 一种改进的抗差 Kalman滤波方法在精密单点定位中的应用[J]. 武汉大学学报信息科学版, 2015, 40(7): 858-864. Zhang Xiao-hong, Pan Yu-ming, Zuo Xiang, et al. An improved robust Kalman filtering and its application in PPP[J]. Geomatics and Information Science of Wuhan University, 2015, 40(7): 858-864.
[14] Uhlemann M, Gendt G, Ramatschi M, et al. GFZ global multi-GNSS network and data processing results[C]//International Association of Geodesy Symposia. 2016: 673-679.
[15] Guo Jing, Xu Xiao-long, Zhao Qi-le, et al. Precise orbit determination for quad-constellation satellites at Wuhan University: strategy, result validation, and comparison[J]. J Geod, 2016, 90(2): 143-159.
Robust Kalman filtering based on different satellite types and it’s application in GPS/BDS precise point positioning
WANG Yan1,2, ZHANG Chuan-ding2, HU Xiao-gong3, SONG Ye-zhi3, MA Shao-long4, TANG Cheng-pan3, LI Ran3
(1. Institute of Surveying and Mapping, Information Engineering University, Zhengzhou 450052, China; 2. Beijing Satellite Navigation Center, Beijing 100094; 3. Shanghai Astronomical Observatory, Chinese Academy of Sciences, Shanghai 200030, China; 4. Nanjing Army Command College, Nanjing 210045, China)
A robust Kalman filtering is used to control the abnormal errors of observations in GNSS dynamic navigation and positioning. However, when it is used in combined GPS/BDS dynamic precise point positioning (PPP), the positioning accuracy may be worse than that of the single system PPP. Since the random characteristics of different types of satellite’s observables are different, the post-fit residuals of these observables are different either. When the post-fit residuals are used to calculate the equivalent weight factor in robust estimation, the high quality data may be down weighted, leading to the deviation of the positioning result. So the advantage of combining GPS/BDS with PPP is weakened. To solve this problem, the equivalent weight factor calculation based on different satellite types in robust Kalman filtering is proposed and the execution process of the algorithm is given. Finally, the experiment based on MGEX data is carried out. Compared with the robust Kalman filtering, the proposed algorithm improves the positioning accuracy and reliability of GPS/BDS with PPP. The positioning accuracy in ENU directions are increased by 34.6%, 33.3%, and 31.0%, respectively.
robust estimation; Kalman filtering; satellite classification weighting; GPS/BDS; precise point positioning
P227
:A
2016-08-25;
:2016-11-28
国家自然科学基金(41374038,41204022,41504018)
王琰(1990—),男,博士研究生,从事测量数据处理理论与方法研究。E-mail: wang1yan.hi@163.com
1005-6734(2016)06-0769-06
10.13695/j.cnki.12-1222/o3.2016.06.013

