复杂曲面自动铺丝轨迹规划算法设计

孟书云　赵东标　陆永华

1.南京工程学院,南京,211167　　2.南京航空航天大学,南京,210016



复杂曲面自动铺丝轨迹规划算法设计

孟书云1赵东标2陆永华2

1.南京工程学院,南京,2111672.南京航空航天大学,南京,210016

摘要：针对复杂曲面自动铺丝轨迹生成问题,提出一种可自动生成铺丝轨迹的经线包络法,即按照曲面形态，自适应生成一族包络整个曲面的经线,然后以此作为参考线，根据复合材料铺丝束纤维的宽度、数量等工艺数据，生成与对应参考线成固定铺放角度的铺丝轨迹。该算法适用于采用参数方法描述的复杂曲面，仿真实例表明该算法可行且有效。

关键词:复杂曲面;铺丝;经线包络法;复合材料

0引言

复杂曲面自动铺丝轨迹规划技术是复合材料构件自动化制造的关键技术之一,国外学者早在20世纪90年代就展开了深入研究，依托先进的CAD/CAM技术，开发出了商用复合材料自动铺丝软件系统。而国内由于高技术禁运以及工艺和装备技术落后的原因，对此技术仍处于摸索研究阶段。

自动铺丝轨迹规划方法主要包括以下几类:等距法、与参考线成固定角度法、等距螺旋法、基于应力分布的Fiber Steering法、投影法等。

国内外学者研究最多的是如何构造初始铺丝参考轨迹。Lewis等[1]首次提出自然路径概念进行铺丝轨迹规划并获得专利,并在商业软件中得到应用;Shinno等[2]提出适用于四边形网格曲面的测地线迭代算法进行轨迹规划；Waldhart[3]提出按照初始参考线法线方向平移得到参考线族的方法来规划铺丝路径；Kurt等[4]提出了以0°铺丝轨迹为基础的由分段曲线拟合的初始参考线设计方法；Shirinzadeh等[5-6]针对开曲面，将特征平面与铺放曲面的交线作为初始参考线来生成铺丝轨迹。国内学者针对铺丝轨迹设计亦展开了大量研究:胡斌等[7]采用遍历法对网格化曲面进行铺丝路径规划，以构件承力总方向作为铺丝参考；李俊斐等[8]通过构造面内和面外两类不同的参考线，针对网格化曲面进行固定角度铺丝路径规划；尹纪龙等[9]先构造类回转体构件的中心线，再以中心线为参考生成铺丝轨迹，进而得到铺丝面；卢敏等[10]探讨了铺丝路径的优化方法。

出于构件承力考虑，往往沿主应力方向和次应力方向铺放丝束以克服拉(压)应力和剪应力。由于型面曲率存在变化，当铺丝束以一定角度铺放时，铺丝束纤维间会产生间隙或重叠，为此，本文提出一种既考虑曲面曲率变化、又满足铺放角度要求的算法即经线包络法。该方法以复杂曲面为铺丝对象，根据曲面信息、铺丝束纤维数、每根纤维宽度、铺丝头运动速度等加工工艺信息，构造自适应的芯模曲面包络线作为参考线族。基于该参考线族，设计出与参考线成一定角度的复合材料铺丝束的轨迹。该算法充分利用曲面的几何性质构造主干参考线，即根据铺丝束纤维数，密化主干参考线，形成曲面包络网。

1主参考线的构建

将非均匀三次有理B样条方法构造的复杂曲面作为研究对象，在不同参数域上构造出由多个曲面片光滑连接而成的复杂曲面。则曲面局部区域可表示为

(1)

其中,控制顶点di,j为曲面m1×n1阶控制网格矩阵;Ni,k(u)、Nj,l(v)分别是u向k次和v向l次的规范B样条基函数,分别由u向节点矢量U=(u0,u1,…,um1+k+1)和v向节点矢量V=(v0,v1,…,vn1+l+1)确定;ωi,j为控制顶点di,j的权因子。

如图1所示,设共有p条主参考线,取曲面边界作为初始参考线,用LI(I=0)表示。即令曲面S(u,v)上参数u=0(此处假设参数u=0,亦可令v=0),得到一条v向参数线作为第一条主参考线,可表示为

(2)

其中,C0为参数u取值为0时对应的规范B样条基函数,C0=(c0,c1,…,cm1)。

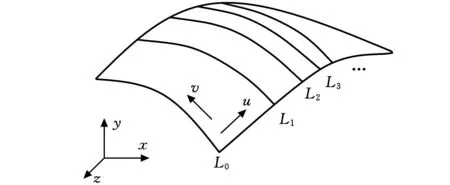
图1　主参考线分布示意图

其余主参考线LI(I=1,2,…,p-1)均采用等参数线。如何确定每条主参考线LI对应的曲面参数值uI成为关键。建立曲面坐标系(均以v向参数线进行说明),相邻下一主参考线LI+1的参数值uI+1是在前一主参考线LI的参数值uI上增加一个适当的值ΔuI形成的，即

uI+1=uI+ΔuI

(3)

将uI+1作为新的参数值,再代入式(2)得到新的主参考线LI+1。

要求出相邻的下一条主参考线参数值,关键是要根据铺丝纤维数m、预浸带单根纤维的宽度b以及与参考线所成的固定角度θ等因素，确定出相应的参数值增量ΔuI。图2中粗实线为主参考线在参数域中的映射，由于曲面存在曲率，故这些主参考线的映射是一族非等距线,即ΔuI≠C(I=1,2,…,p-1；C为常数)。

图2　主参考线在参数域的映射图

如图3所示,设与主参考线LI成固定铺放角θ的第I条铺丝束内第J条路径为KI,J(I=0,1,…，p;J=0,1,…,m-1)，若该路径起点为M,则M∈LI且M∈KI,J，应有下式成立：

(4)

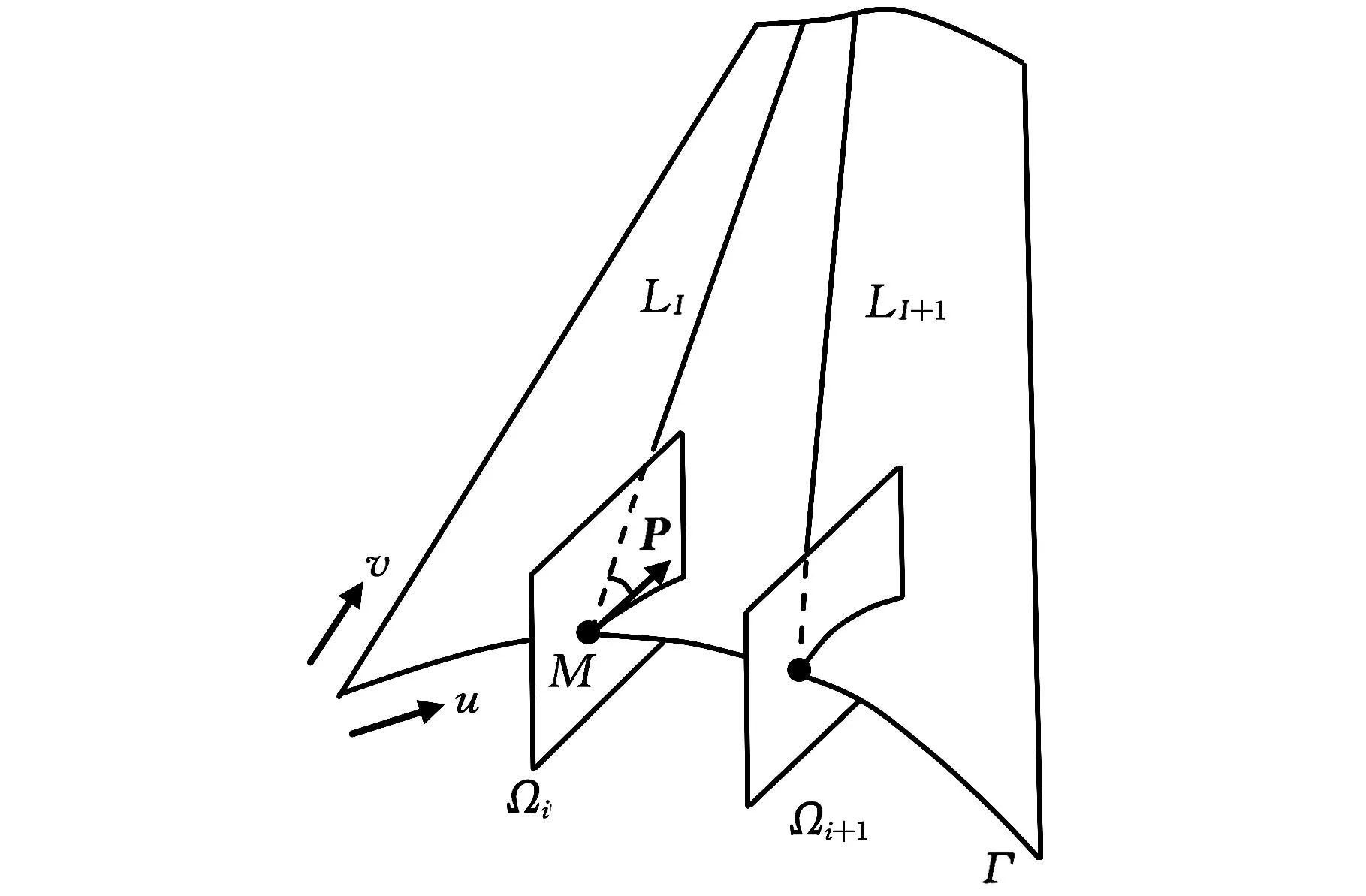
图3　主参考线计算原理图

通过式(2)可求得

(5)

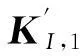
∫λS(u,v)ds=mb

(6)

其中，曲线λ是曲面S(u,v)上一条分段连续的曲线,即若在点M处构建曲面的Frenet活动标架,从法面与曲面S(u,v)的交线即为曲线λ中的一段；s为弧长参数。

从物理意义上来讲,式(6)是单条铺丝束在曲面边界曲线Γ上所占幅宽。很明显,通过式(6)不能直接求解出相邻铺丝束同侧边界路径的起点。考虑到工业上为提高加工效率，常采用多根宽度为1/8″、1/4″或1/2″(注：1″≈2.54 cm)等规格的预浸带纤维并列铺放,单根纤维丝宽度与铺放型面的尺寸相比相差悬殊,故应用“分割+投影+累加求和”的方法，逐条计算满足要求的主参考线起点。

如图4所示,在点M和点N之间构建m-1个平面,保证相邻平面间沿铺丝方向法向的曲线距离为单根纤维丝的宽度。在点M(Mx,My,Mz)处构建Frenet标架,曲面S(u,v)的法面Ωi经过点M处的铺丝轨迹方向τ=(α,β,γ),那么从法面在曲面上的投影即有向曲线段MC1(用Q(r)(r≥0)表示)的长度应为b，则Q(r)表示为

(7)

且满足

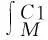
(8)

图4　相邻主参考线起点计算原理图

通过式(7)和式(8)联立求解,得到满足单根纤维铺丝宽度的轨迹点C1(用Sx(uc1,vc1),Sy(uc1,vc1),Sz(uc1,vc1)表示)。过点C1作面Φ1//Ωi,则平面Φ1与曲面边界曲线Γ的交点C2可表示为

(9)

其中,E0为曲面S(u,v)上的参数v取值为0时对应的规范B样条基函数,E0=(e0,e1,…,en1)。

同理可作出垂面Φ2,得到Φ2与曲面边界曲线Γ的交点C4。根据要求的曲面边界曲线处铺丝束纤维的铺放角度和宽度，若铺丝束由m条纤维组成，则重复上述过程，基于Frenet标架构建m-1个从法面及m个法面的平行平面,延伸第m个平行平面与边界曲线Γ相交,交点就是相邻的下一条主参考线的起始点N。

2铺丝轨迹的设计

以主参考线为基准,分两步生成铺丝路径。第一步:构造出每条铺丝束的左(或右)边界铺丝路径，保证该路径与主参考线成固定角度;第二步:从边界铺丝路径开始,依次平行等距生成同一铺丝束中的每条纤维的路径。

2.1不同铺丝束的边界纤维的铺丝路径

如图5所示,已知位于曲面S(u,v)上同时也是单条铺丝束边界纤维路径上的任一点Bi(ui,vi),该条路径上的下一点设为Bi+1。设主参考线Li上与点Bi的对应点为Ai,由式(2)可得曲面在点Ai处的v向切矢量τAi为

(10)

(11)

式中,定义B样条基Nj,l(v)的节点矢量为(v0,v1,…,vn1+l+1)。

图5　单条铺丝束边界纤维轨迹生成原理图

由于τAi为铺丝轨迹的参考方向,设点Bi处新的铺丝方向向量为τBi,则点Bi处曲面的密切平面内存在如下关系：

cosθ=τAi·τBi

(12)

设点Bi处曲面的密切平面的法矢量为NBi,则通过

τBi=τAi·T·R(ΝBi,θ)·T-1

(13)

可以得到该点处的铺丝方向矢量。式中T和T-1分别是将点Bi平移到坐标系原点的矩阵和逆矩阵;R(NBi,θ)是绕曲面法矢量NBi旋转θ角的变换矩阵。

结合铺丝头运动控制的特点，假设铺丝头运动速度为v、运动控制周期为Δt,相邻下一轨迹点为Bi+1，则满足

lBiBi+1=v·Δt

(14)

式中,lBiBi+1为点Bi到点Bi+1的弧长矢量。

设点Bi的坐标为(XBi,YBi,ZBi)，曲面在点Bi处的法矢量为NBi，由式(13)得到的点Bi处的铺丝轨迹方向矢量为TBi。构建一平面Φ,使NBi∈Φ,TBi∈Φ。则平面Φ与曲面S(u,v)的交线η(t)=(x(u(t),v(t)),y(u(t),v(t)),z(u(t),v(t)))为

(15)

其中,平面Φ的法矢量用矢量B=(Bx,By,Bz)表示。

由式(14)可知，待求的下一铺丝轨迹点Bi+1表达为

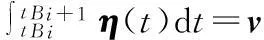
(16)

由式(16)得到点Bi+1对应的参数t,进而求出铺丝轨迹点Bi+1的坐标。

2.2同一预浸带中每条纤维的轨迹生成

设同一铺丝束中有并列的铺丝纤维m条，在前述逐点生成边界纤维的轨迹后，从左到右依次平行等距生成剩余的m-1条纤维的铺丝轨迹。为了保证同一铺丝束内多条纤维间无缝隙和重叠，应使每条纤维轨迹间保持等距。

由于芯模表面为不可展曲面，这就意味着相邻纤维轨迹间的最短曲面距离(即测地线)必须保持为恒定值。而欲知曲面上任意两点间的测地线长度，需进行大量较为繁复的计算。

如图6所示,已知前一铺丝轨迹上离散点Bi,设曲面沿轨迹在Bi(xB,yB,zB)点处的切矢量为lBD,用T=(Tx,Ty,Tz)表示,则平面Φ为

Tx(x-xB)+Ty(y-yB)+Tz(z-zB)=0

(17)

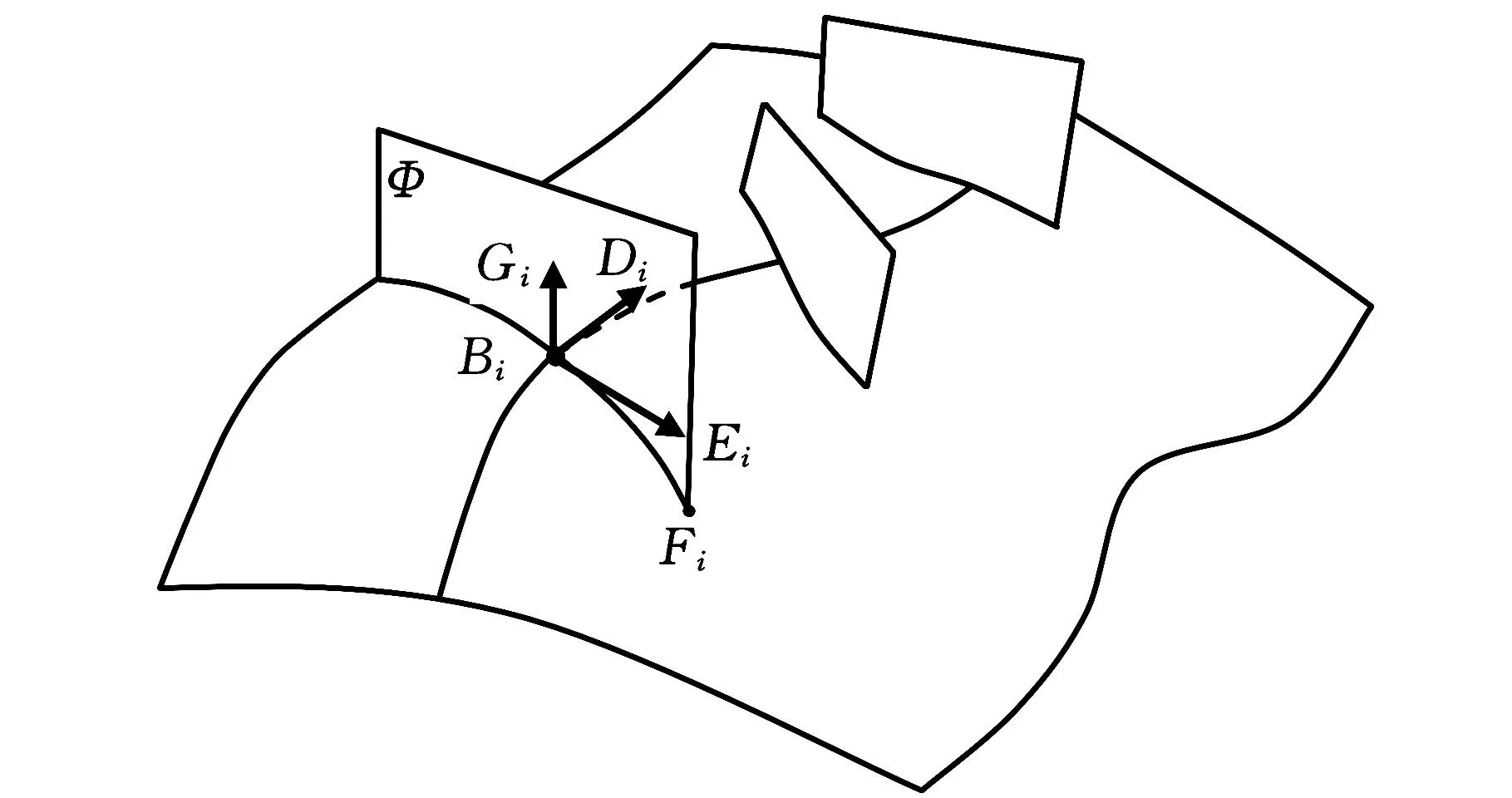
图6　同一铺丝束内其余纤维轨迹生成原理图

联立式(1)和式(17),得到平面Φ与曲面的交线L,若有向交线L采用参数方程表示,即

L=f(t)t∈[0,+∞)

(18)

其中点Bi处的参数值t为0,并令曲线L的正向为图6所示的lBiEi方向。由曲面在Bi点处的法矢量lBiGi和切矢量lBiDi,可得矢量lBiEi的方向矢量是

lBiEi=lBiDi×lBiGi

(19)

那么存在如下关系

(20)

由式(20)可以得到相邻轨迹的下一铺丝点。

构建一族平面,依次通过前一条轨迹上一系列离散点,并以边界轨迹在相应离散点处的切线为平面的法线,通过用该系列平面与曲面的交线，可间接得到相邻铺丝轨迹上有序的离散点。

3实例分析

本文提出的算法以三次非均匀有理B样条方法重建的铺丝芯模表面作为数学模型,实现了复杂曲面上以不同角度铺放具有不同纤维数的铺丝束时的算法仿真。

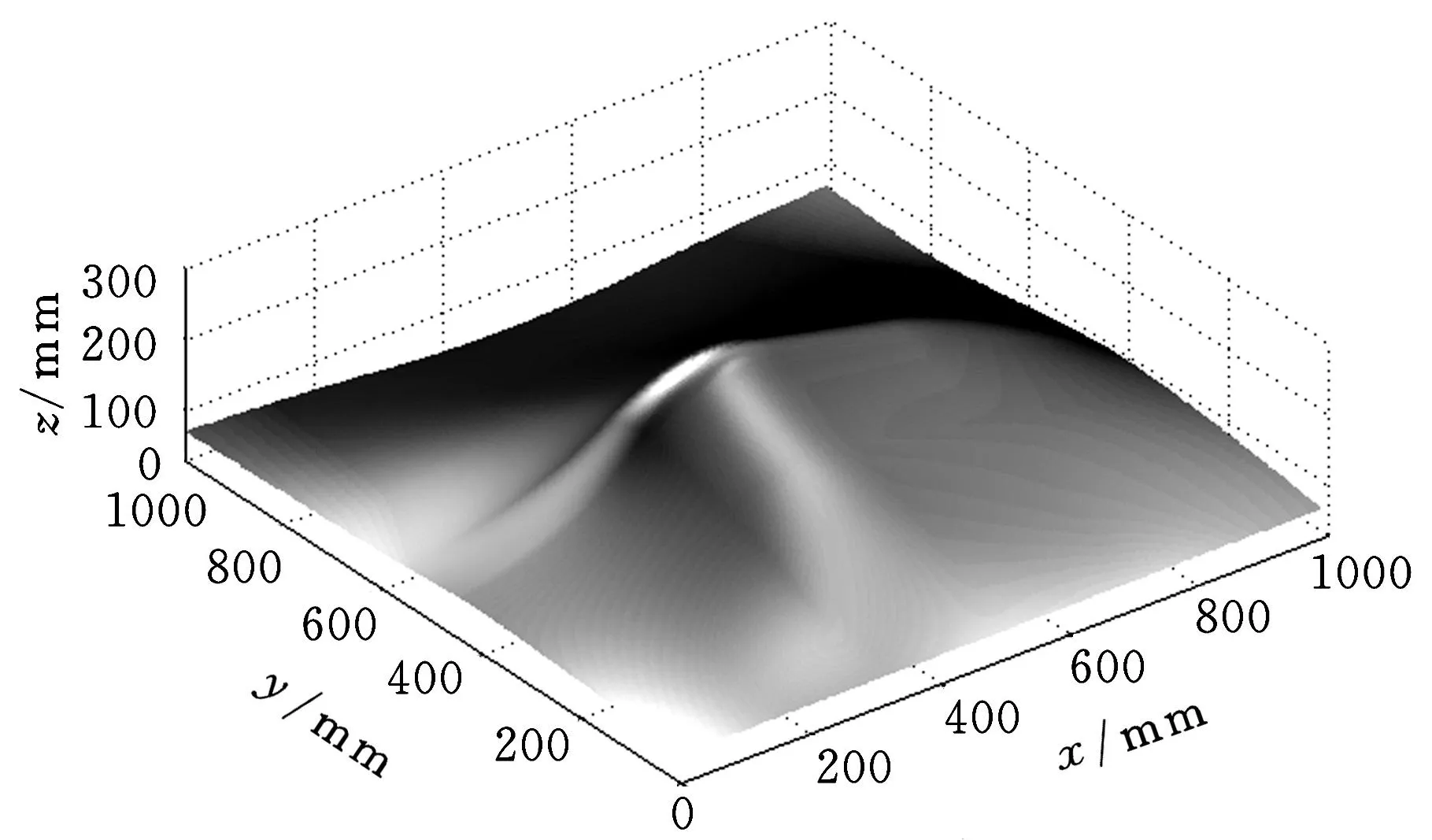
图7　铺丝型面

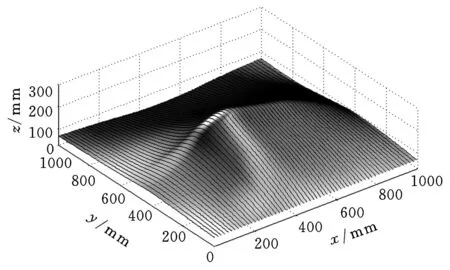
图8　包络曲面的经线参考线族

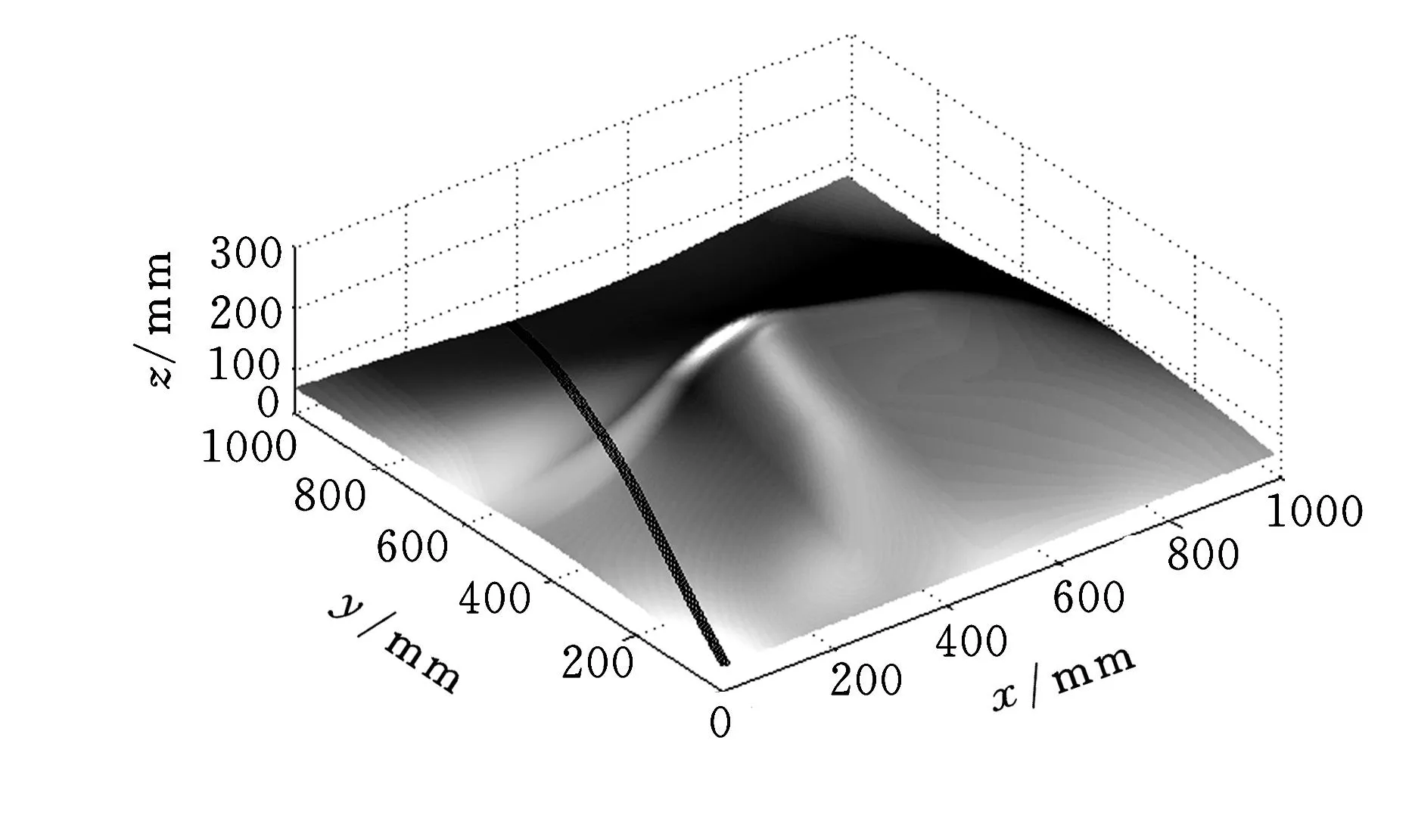
图9　铺放角θ=20°时一条铺丝束路径

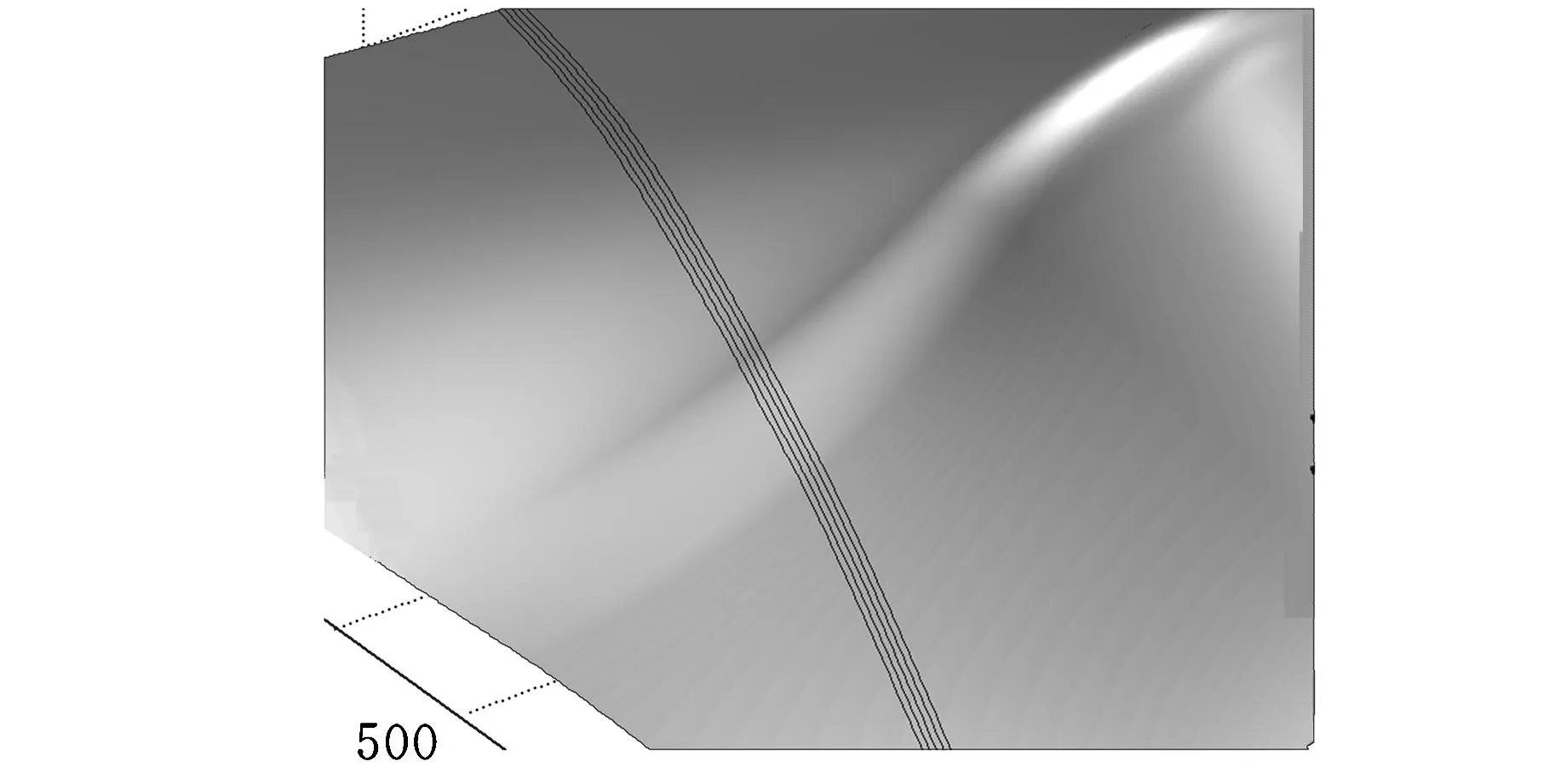
图10　铺丝束路径局部放大图

图11　铺放角θ=20°时两条铺丝束路径

图12　铺放角θ=20°时三条铺丝束路径

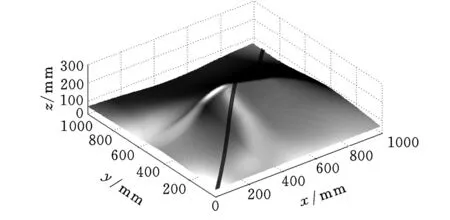
图13　铺放角θ=45°时一条铺丝束路径

图7为采用三次B样条方法给出的待铺丝的复杂曲面重建模型;图8给出了当铺丝束中有5根纤维、每根纤维宽度为1/4″时生成的不同参考线;图9给出了铺丝头运动速度为30m/min且运动控制周期为0.01ms时,铺丝束中有5根纤维、每根纤维宽度为1/4″、与参考线族成20°铺丝角时的一条铺丝束路径;图10为铺丝束路径局部放大图;图11给出了铺丝头运动速度为30m/min且运动控制周期为0.01ms时,铺丝束中有5根纤维、纤维宽度为1/4″、铺丝角为20°时的两条铺丝束路径；图12给出了铺丝头运动速度为30m/min且运动控制周期为0.01ms时，铺丝束中有5根纤维、纤维宽度为1/4″、铺丝角为20°时的三条铺丝束路径；图13给出了铺丝头运动速度为30m/min且运动控制周期为0.01ms时,基于参考线生成的单条铺丝束轨迹,铺丝束中有5条纤维，每根纤维宽度为1/4″,与参考线族成45°铺丝角。

4结论

(1)对于用参数方法描述的复杂曲面，本文给出了自动铺丝轨迹规划算法——经线包络法。基于自适应生成的参考线族，利用铺丝头的加工运动工艺参数，通过与相应参考线成固定铺放角度，逐点有序生成铺丝束纤维的铺丝轨迹。

(2)求取轨迹过程中利用微分几何原理，多次运用投影法，结合铺丝头运动学参数，合理近似得到铺丝轨迹上的一系列等距离散点，避免了曲面曲率的计算和曲面上任意两点间测地线长度计算的问题。

(3)仿真结果表明，采用该算法可生成铺丝路径，算法可行有效。

参考文献：

[1]LewisHW,RomeroJE.CompositeTapePlacementApparatuswithNaturalPathGenerationMeans:US,DE3727462[P].1987-08-18.

[2]ShinnoN,ShigematsuT.MethodforControllingTapeAffixingDirectionofAutomaticTapeAffixingApparatus:US,5041179[P].1991-08-20.

[3]WaldhartC.AnalysisofTow-placed,VariableStiffnessLaminates[D].Blackburg:VirginiaPolytechnicInstituteandStateUniversity,1996.

[4]KurtS,JamesM,RichardH.ApproximateGeometricMethodsinApplicationtotheModelingofFiberPlacedCompositeStructures[J].JournalofComputingandInformationScienceinEngineering,2004,4(9):251-256.

[5]ShirinzadehB,GurselA,CheeWF,etal.FabricationProcessofOpenSurfacesbyRoboticFibrePlacement[J].RoboticsandComputerIntegratedManufacturing,2004,20(1):17-28.

[6]ShirinzadehB,CassidyG,OetomoD,etal.TrajectoryGenerationforOpen-contouredStructuresinRoboticFibrePlacement[J].RoboticsandComputerIntegratedManufacturing,2007,23(4):380-394.

[7]胡斌,徐东亮.基于遍历法的开放曲面铺丝轨迹规划[J].玻璃钢/复合材料,2014(6):20-24.

HuBin,XuDongliang.FiberPlacementPathPlanningforOpenSurfacesBasedonTraversalMethod[J].FRP/CM,2014(6):20-24.

[8]李俊斐,王显峰,肖军,等.网格化曲面的固定角度铺丝轨迹规划算法[J].计算机辅助设计与图形学学报,2013,25(9):1410-1414.

LiJunfei,WangXianfeng,XiaoJun,etal.TrajectoryPlanningofAutomatedFiberPlacementforMeshedSurfaceinFixedAngleAlgorithm[J].JournalofComputer-aidedDesign&ConputerGraphics,2013,25(9):1410-1414.

[9]尹纪龙,沈景凤,章志东.复合材料自动铺丝轨迹规划[J].玻璃钢/复合材料,2014(3):8-12.

YinJilong,ShenJingfeng,ZhangZhidong.PathPlanningforCompositeFiberPlacement,FRP/CM,2014(3):8-12.

[10]卢敏，周来水,王小平.一种基于投影法的铺丝路径优化生成算法[J].中国机械工程,2011,22(16):1993-1996.

LuMin,ZhouLaishui,WangXiaoping.OptimizationofFiberSteeringinCompositeLaminatesUsingaCurveProjectionAlgorithm[J].ChinaMechanicalEngineering,2011,22(16): 1993-1996.

(编辑王艳丽)

Design of Path Planning Algorithm for Automatically Fiber Placement for Sculptured Surfaces

Meng Shuyun1Zhao Dongbiao2Lu Yonghua2

1.Nanjing Institute of Technology,Nanjing,211167

2.Nanjing University of Aeronautics and Astronautics,Nanjing,210016

Abstract:Aimed at path generation for automatically fiber placement of sculptured surfaces,an algorithm called WEM was proposed.A family of wraps as the reference lines were adaptively generated based on the surface shape. According to the process data of the fibers for composite tow, fiber placement path were obtained,which formed fixed placement angle with the corresponding reference curve.This algorithm might be applied in the kind of free-form spline surface with parametric method description. The simulation shows that the algorithm is feasible and effective.

Key words:sculptured surface;fiber placement;warp envolopment method(WEM);composite

作者简介：孟书云，女，1978年生。南京工程学院自动化学院副教授。主要研究方向为先进数控技术、数控加工、CAD/CAM等。发表论文10余篇。赵东标，男，1963年生。南京航空航天大学机电学院教授、博士研究生导师。陆永华，男，1977年生。南京航空航天大学机电学院副教授。

中图分类号:TB33;TP391.73

DOI：10.3969/j.issn.1004-132X.2016.05.017

基金项目：国家自然科学基金资助项目(51175261);高等学校博士学科点专项科研基金资助项目(20123218110020);国家重点基础研究发展计划(973计划)资助项目(2014CB046501);江苏省重点建设学科经费资助项目

收稿日期：2015-02-24