囊式负压空气隔振器力学建模与性能研究

盛国才　李　吉　王建维

大连大学，大连，116622



囊式负压空气隔振器力学建模与性能研究

盛国才李吉王建维

大连大学，大连，116622

摘要：以低频隔振器为研究对象，利用负压空气独有的特性，结合橡胶良好的弹性性能，提出了囊式负压空气隔振器的全新概念，对负压隔振原理进行了定性分析。力学建模分析、理论仿真分析以及实验验证结果表明，所建立起来的隔振系统具有理想的非线性弹性曲线。同时研究了负压大小和有效面积对性能的影响。最后得出，囊式负压空气隔振器可以获得理想的低频隔振效果，有很强的实用性。

关键词：负压；低频；隔振；刚度特性

0引言

目前对于低频隔振通常采用空气弹簧、多级隔振系统、主动式隔振[1]、磁悬浮隔振、其他组合及串并联隔振[2-3]等方式。Le等[4]针对汽车座椅采用两负刚度弹簧并列对称放置的方法设计了对0.5～5 Hz隔振效果较好的隔振系统。Alabuzhev 等[5]论述了准零刚度隔振系统的理论及设计方法。徐道临等[6]提出了一种阻尼扰动控制方法，拓宽了准零刚度隔振系统的有效隔振频率区间。Carrela等[7]和Kovacic等[8]提出了包括一个垂直弹簧和两个斜弹簧的准零刚度隔振器。王家胜[9]对带有附加气室的空气弹簧性能作了实验测试研究和力学特性分析，论证了通过附加较大气室可以获得较低的刚度特性的结论。高红星等[10]对空气弹簧建立了一种多物理参数的非线性模型。带有辅助气囊的空气弹簧和主动隔振技术虽然可以获得较好的低频隔振效果，但普及仍有困难，甚至是不可能的。这些方式虽能有效降低系统的固有频率，但大多因结构复杂，占用空间大，造价昂贵，且需外加控制系统，能量消耗大，使这些隔振措施很难在实际工程中得到广泛应用，因此有必要设计研究一种通用的有良好低频隔振效果的新型隔振器。

笔者在前期研究基础[12-13]上，设计了囊式负压空气隔振器，并探究其隔振原理及特有的低频隔振性。

1隔振原理分析

囊式负压空气隔振器主要由帘线橡胶复合气囊、上下受力面板、内部平衡支撑部件、固定连接部件等组成。由于腔室内呈现负压状态，所以外部大气压会作用在整个结构外壳上。帘线橡胶复合气囊由内密封胶层、外密封胶层、帘线和橡胶硫化层构成，密封层主要是为内部腔室提供负压或真空的状态，内部支撑部件保持初始横向稳定性，防止由于负压的作用而使橡胶囊出现瘪曲现象，减小了负压腔室的容积，帘线及橡胶硫化层则为主要受力部件。囊式负压空气隔振器结构见图1。

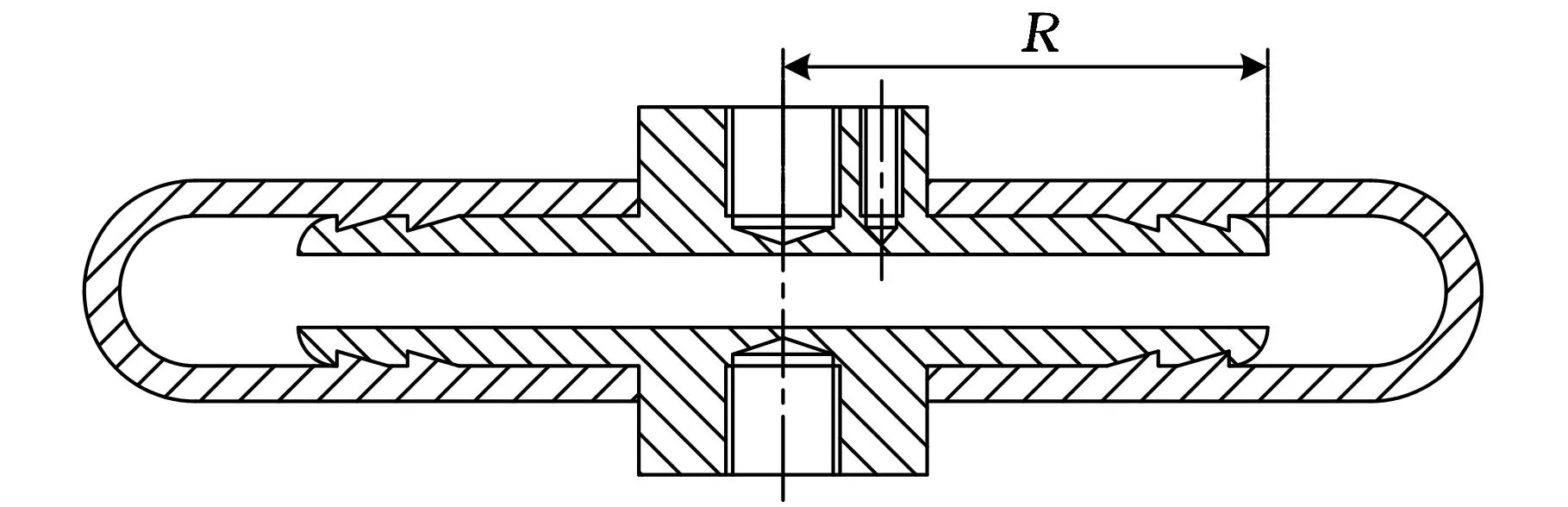
图1　结构简图

首先只考虑空气负压下隔振器刚度特点，考虑一个密闭的气缸。当用力将活塞向外拉出时，缸内将出现负压，随着拉力的增大、活塞位移的增大，缸内真空度逐渐增大，但根据物理学原理，拉力(载荷)与活塞位移并不成正比，而是呈现出图2中空气曲线所示的非线性关系，其特点是初始时刚度较大，随着位移的增大，刚度逐渐减小并趋近于零，这与空气弹簧的特性正好相反。

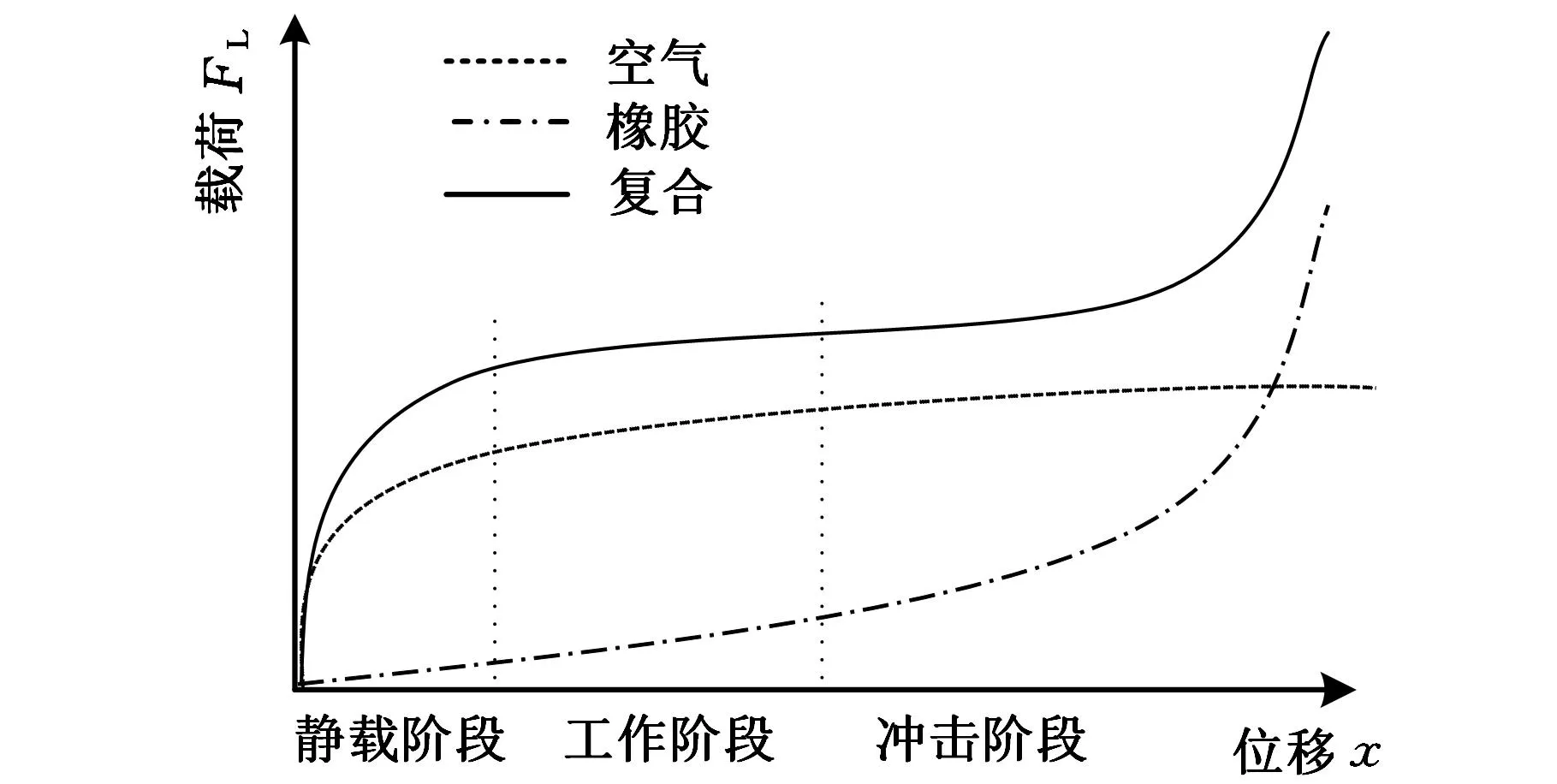
图2　复合位移-载荷曲线

另外考虑一种囊式的橡胶壳。当受到图2中橡胶曲线所示的力作用时，若变形量较小，橡胶外壳只产生弯曲变形，其刚度很小，但当变形过大时，橡胶外壳则产生弯曲拉伸组合变形，其刚度迅速增大，这一特点与上例恰好相反。

上述两种结构各有优缺点，前者无法长期密封且抗冲击能力差，后者抗冲击能力强，但承载能力不足，如果能够将两者结合起来，如图1复合曲线所示，相互补充，既可以在平衡位置附近获得很小的刚度，进而获得很低的固有频率，提高对低频振动的隔离性能，又可以在变形过大时，不会使系统产生过大的偏移，提高系统的抗冲击性能。

2力学建模

固定下面板的垂向位移，则囊式负压空气隔振器的工作原理可用图3表示，因为负压气囊是柔软的橡胶薄膜，根据薄膜理论中一般采用的基本假设，负压气囊不能传递弯矩和横向力，因此可以根据力的平衡条件，确定负压气囊的垂向受力[11]:

F=pS=pπR2

(1)

式中，p为腔室工作压力；S为囊式负压空气弹簧的有效面积；R为有效半径，R不是常数而是随着载荷如图3所示变化。

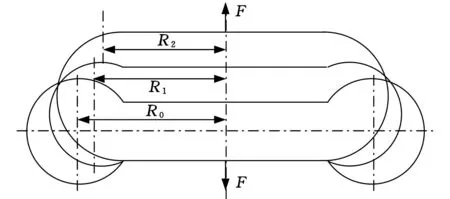
图3　工作原理图

从图3中可以看出，当载荷F增大时，囊式负压空气弹簧的有效半径R将随之减小，最后等于盖板的面积。

一般情况下，气体的状态变化是一个多变过程。在气体的多变过程中，根据气体状态方程，负压腔室内的绝对压力和容积之间存在如下关系：

(2)

式中，pa为大气压力；p0为初始状态腔内压力；m为气体的多变指数，它取决于气体变化过程的流动速度；V0为初始腔体体积；V为腔室工作状态体积。

当拉伸位移为x时，腔室容积增加了dV，根据气体状态方程有：

(3)

又因为dV=Sx，S是关于x的函数，则

振动时，工作腔室中的空气压力因拉伸而变化，振动时载荷F和位移x间的关系为

(4)

显然，载荷F和位移x之间是非线性关系。将式(4)对位移x求导，得刚度计算式：

(5)

经分析可知，当负压腔室接近极限时，即只有负压腔室承受主要载荷达到最大值附近时，此时位移变化较小，刚度最低：

即

(6)

由式(6)可以看出，囊式负压空气隔振器在负压载荷达到极限时，刚度由两项组成，可以看成图4所示的力学模型，由一个正刚度和一个负刚度并联而成。

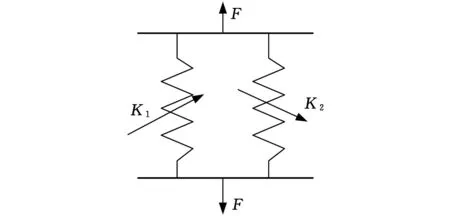
图4　囊式负压空气隔振器力学模型

从式(6)中可以看出，如果有效承载面积变化率dS/dx与S2/V0接近，则可以获得接近零刚度的模型。有效载荷面积和负压容积之比越大刚度越低，所以可以通过调节负压腔室的横截面积大小来改变刚度特性；囊式负压空气弹簧的刚度K和它在变形时的有效面积变化率有关，dS/dx 越小，刚度越低，但前后两项相互关联；初始腔体压力对刚度也有非线性影响。

要计算囊式负压空气隔振器的刚度，必须知道其有效承载面积变化率dS/dx，而dS/dx与囊式负压空气隔振器的几何形状有关，故可以通过仿真计算得出不同几何形状的刚度曲线。

3实验与特性分析

囊式负压空气隔振器的非线性模型是通过有限元法来进行仿真分析的，考虑到模型的高度非线性，选用ABAQUS去求解这种耦合的高度非线性的准静态问题。

整个囊式负压空气隔振器的计算模型如图5所示，考虑到上下受力面板变形较小，本文将其定义为刚性部件，主要技术参数为：帘线材料选用线弹性材料，弹性模量E=210.0 GPa，泊松比ν=0.3，方向角为±45°，铺设两层。橡胶选用Mooney-Rivlin本构模型，橡胶参数通过单轴、双轴拉伸试验获得。负压空气隔振器主要技术指标为：有效设计高度55 mm，最大直径180 mm，橡胶帘线硫化层厚6 mm，上下面板半径Rm=70 mm，其值约等于有效半径。

图5　计算模型

在刚度特性计算时，约束下面板的6个自由度，接触分析采用硬接触，橡胶囊采用壳单元(S4R)计算，共计496个单元，上下面板采用表面单元(SFM3D3)计算，共计88个单元，腔体采用基于表面的流体单元(surface-based fluid cavities)计算。在有限元分析时，适当延长迭代时间，以提高分析精度，为获得负压腔室压力、有效面积等因素对刚度的影响，分别对各个参数取不同的数值进行分析计算。

对有限元模型，采用分步加载的方式定义腔体初始压力，为保证在加载负压的分析步中负压空气隔振器仍处于自然状态，约束上面板6个自由度，定义有限元模型初始腔室内压力为16.36 kPa，即施加-85 kPa的负压载荷。在施加负载分析步中，撤去上面板垂向自由度约束，同时，在上受力面板上施加10 kN载荷，下受力面板仍保持约束6个自由度，得到载荷力F(N)与位移(m)数据。

对实物模型，根据国标GB/T15168-2013中的实验测试方法，对负压空气隔振器作抽真空处理，保留内压约为16.36 kPa。然后在WDW-100型微机控制式电子万能试验机上进行静态实验，施加10 kN的力，如图6所示，得到载荷力和位移数据。仿真分析数据和实验测试数据如图7所示。

图6　实验现场及变形放大照片

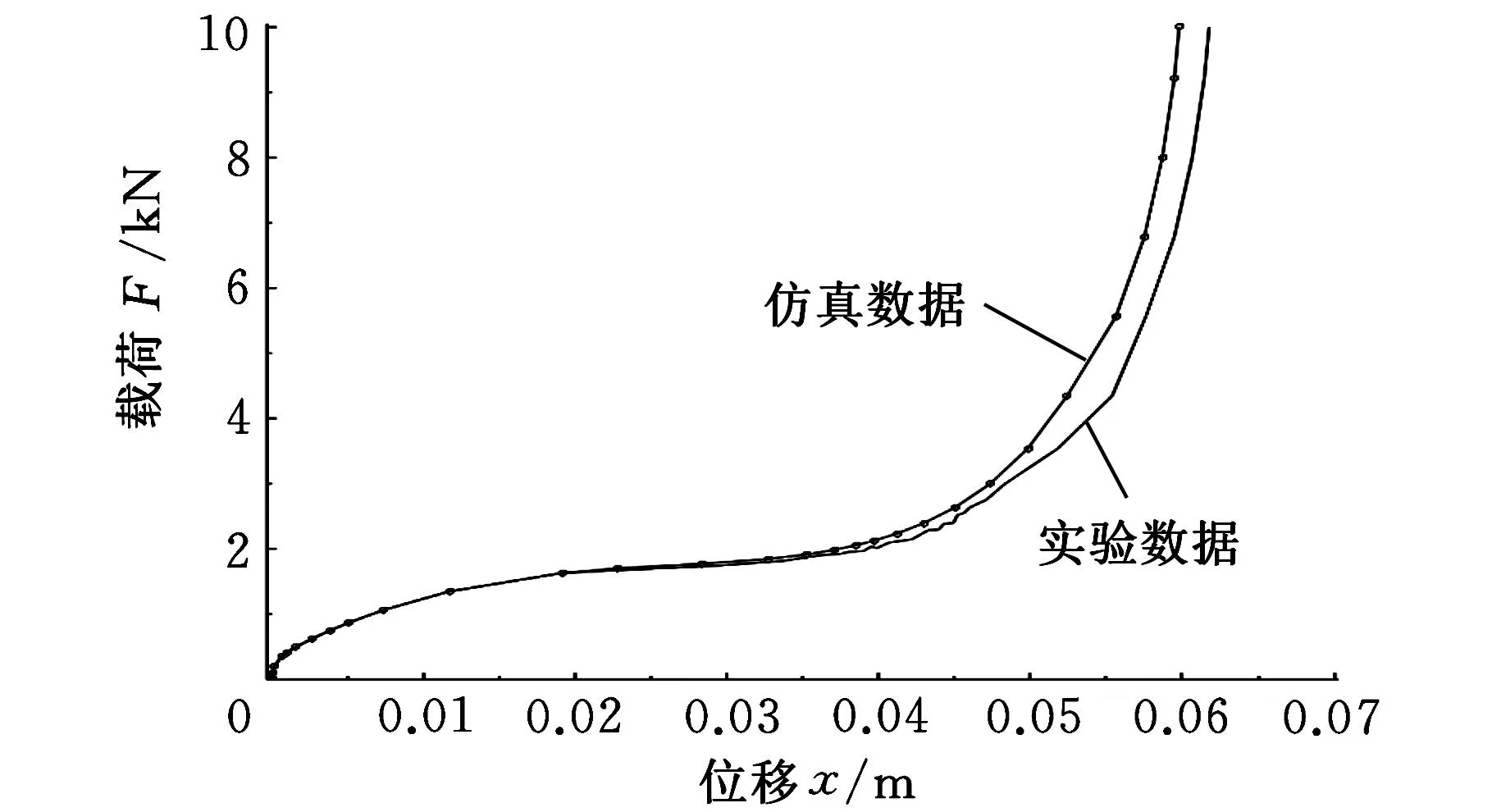
图7　实验及仿真特性曲线

从图7可以看出：负压空气隔振器有限元仿真计算曲线和实验曲线基本吻合，尤其是在工作行程30 mm以内两曲线基本重合，随着行程的增大，两曲线出现偏差，但两曲线走势仍然一样。这验证了应用有限元模型分析的正确性。两种曲线的非线性度都较大，在22.5～32.5 mm工作行程时特性曲线刚度接近于零，说明负压空气隔振器在此行程下可以获得准零刚度特性，此时的承载力在2 kN左右，能满足应用要求，说明可以定义22.5～32.5 mm为额定工作载荷区间，2 kN可以定义为额定载荷，在此工作区间或额定载荷下可以保证仪器设备具有较低的振动频率。进一步分析表明，0～20 mm可以看作静载阶段，随后曲线刚度迅速增大说明抗冲击能力较大，50～60 mm可以定义为抗冲击工作区间。

3.1负压腔室压力大小对特性的影响

根据图5的计算模型，分别对负压腔室施加不同大小的压力，得到不同负压腔室压力大小作用下的载荷位移特性曲线，如图8所示，采用分步加载的方式，首先对负压腔室施加30 kPa、45 kPa、60 kPa的负压，然后分别施加10 kN的载荷，分析步时长(量纲一)为1。同时计算拉伸过程中的负压腔室压力随分析步时间变化的数值曲线，如图9所示。计算负压腔室压力随拉伸位移变化的数值曲线，如图10所示。

1.p0=30 kPa　2.p0=45 kPa　3.p0=60 kPa图8　不同负压大小时的载荷-位移特性曲线

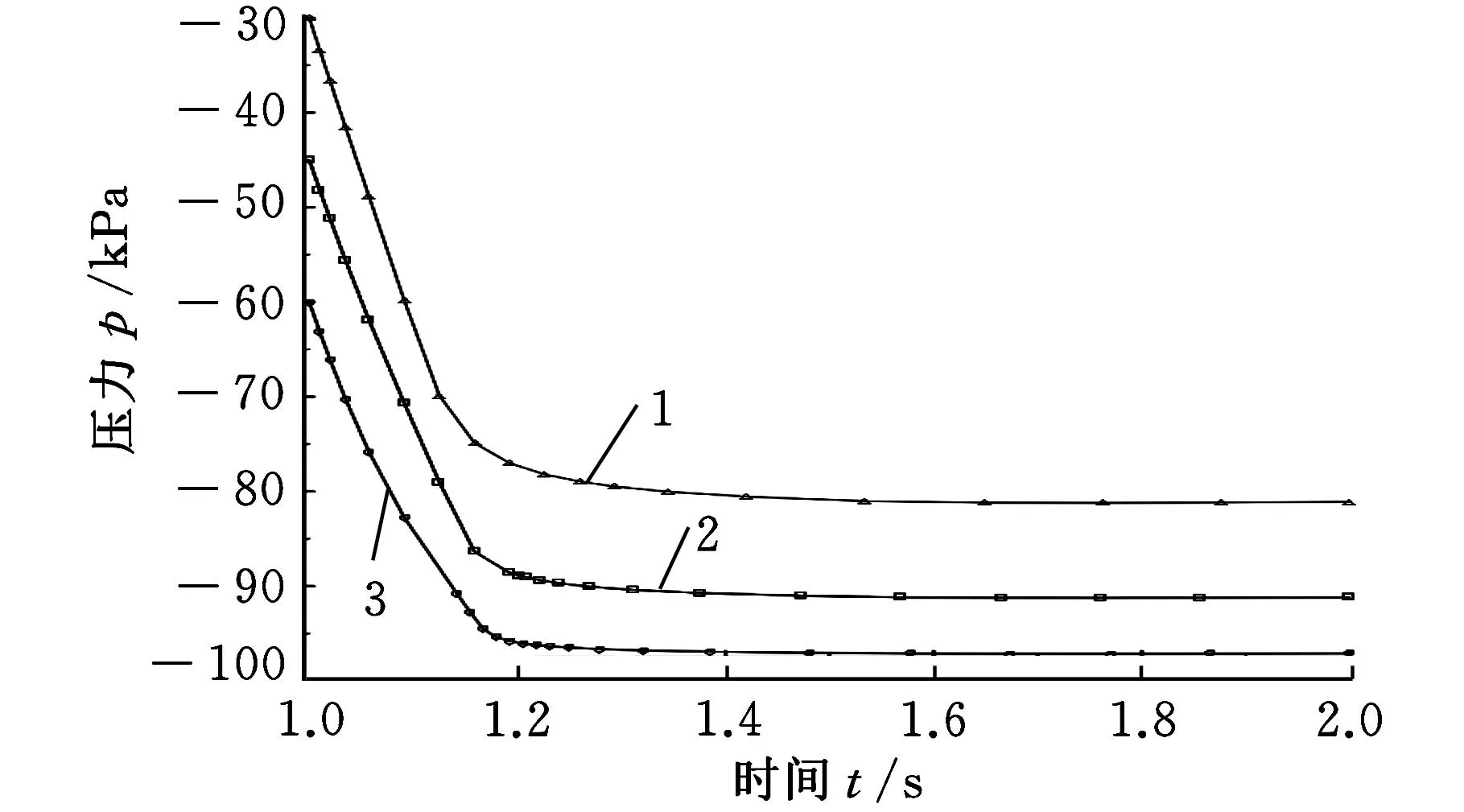
1.p0=30 kPa　2.p0=45 kPa　3.p0=60 kPa图9　不同初始负压下压力-时间关系曲线

1.p0=30 kPa　2.p0=45 kPa　3.p0=60 kPa图10　不同初始负压下压力-位移关系曲线

由图8可以看出，三条曲线的非线性度都很大，均呈现出先升高，后平缓，再急剧升高的特性趋势，吻合图2中可以获得低频隔振的原理分析结果。负压值越大，特性曲线在工作阶段越平缓，且带负载能力越大。从图9分析得到，负压腔室压力开始下降迅速，随后趋于稳定。从图10得到，随着拉伸位移的增大，负压迅速增大，且呈现高度的非线性。结合图9和图10可以得出，在整个拉伸过程中，静载阶段载荷随负压值的增大而增大，当达到工作阶段时负压腔室承受主要载荷，随后橡胶囊由前两个阶段的弯曲变形开始转化为拉伸变形，此时，由橡胶帘线硫化层构成的橡胶囊承受主要载荷。

综上可以得出，负压腔室压力的大小对刚度特性有直接影响，且在合理区间内，呈现负压值越大、刚度越小的特性。负压腔室和橡胶的耦合作用构成了高度非线性的弹性特性曲线，且可以得出，当橡胶囊只发生弯曲变形，即负压腔室承受主要载荷时，可以获得准零刚度特性，进而实现超低频隔振效果。

3.2负压腔室有效面积对特性的影响

鉴于有效面积直接取决于有效半径R的大小，本文设置有效半径为60 mm、80 mm，腔内负压均为60 kPa的计算模型，其他约束尺寸、约束边界条件、载荷施加方式及网格划分与图5的计算模型保持不变。这样加上图5计算模型中的R=70 mm，负压为60 kPa的数值曲线，共同构成了如图11所示的不同有效半径(有效面积)的特性曲线。同时计算在不同有效半径下压力与分析步时间的关系曲线，结果如图12所示。计算在不同有效半径下压力与位移的关系曲线，结果如图13所示。

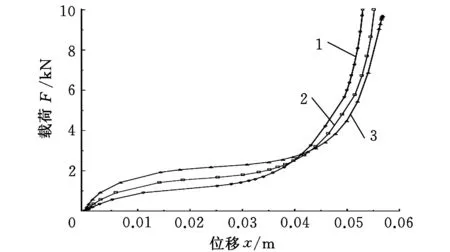
1.R=60 mm　2.R=70 mm　3.R=80 mm图11　不同有效半径的特性曲线

1.R=60 mm　2.R=70 mm　3.R=80 mm图12　不同有效半径的压力-时间曲线

1.R=60 mm　2.R=70 mm　3.R=80 mm图13　不同有效半径的压力-位移曲线

从图11可以看出，不同有效半径的三条特性曲线非线性度都很大，有效半径越大承载力越大，同时曲线在工作阶段越平缓，且平缓段越长。从图12可以看出，在同一初始负压腔室压力下，有效半径越大，拉伸过程稳定阶段的负压值越大，且稳定越晚，同时，根据理想气体状态方程可知，此时囊式负压空气隔振器变形量较小。在图13中，不同有效半径下的负压随位移变化呈现高度的非线性。结合图12和图13的分析可以得出，在整个拉伸过程中，静载阶段载荷随负压值的增大而增大，当达到工作阶段时负压腔室承受主要载荷，随后橡胶囊由前两个阶段的弯曲变形开始转化为拉伸变形，此时由于变形量较小，所以由橡胶帘线硫化层构成的橡胶囊承受主要载荷。

综上可以得出，有效半径直接影响囊式负压空气隔振器的承载力，同时对刚度特性和工作阶段的行程区间大小有一定影响。

结合3.1节和3.2节的分析，可以得出，应用负压原理可以获得准零刚度的隔振特性，进而可以获得低频工作状态，囊式负压空气隔振器的刚度特性主要受负压值大小和有效面积的影响，同时，验证了力学模型的正确性。

4结语

负压隔振理论目前国内外没有可借鉴的研究成果，本研究在前期的研究基础上，建立结构力学模型和计算机仿真分析模型，分别探讨了负压和有效面积对特性曲线的影响，最终获得系统的力学特性。结果表明，负压腔室能够获得较低的刚度特性，并且，如果隔振器工作在额定载荷状态下，系统将在准零刚度点平衡。囊式负压空气弹簧隔振器具有很好的低频隔振效果和一定的抗冲击能力，鉴于负压隔振的良好特性，同时具有结构简单、成本低廉的特性，故能够在船舶动力舱隔振系统、精密仪器隔振系统、发动机隔振系统、车辆及各种通用机械隔振系统中得到广泛应用，因此对提升我国低频隔振的技术水平具有重要意义。

参考文献：

[1]曹青松,李维嘉.一种新型主动隔振系统的建模研究[J]. 中国机械工程，2008,19(6):662-666.

Cao Qingsong,Li Weijia.Study on Modeling of a Novel Active Isolation System[J].China Mechanical Engineering,2008,19(6):662-666.

[2]孟令帅,孙景工，牛福，等.新型准零刚度隔振系统的设计与研究[J]. 振动与冲击,2014,33(11):195-199.

Meng Lingshuai, Sun Jinggong，Niu Fu, et al.Design and Analysis of a Novel Quasi-zero Stiffness Vibration Isolation System[J].Journal of Vibration and Shock, 2014,33(11):195-199.

[3]闫菲，车驰东.变刚度隔振系统动力特性及仿真[J]. 噪声与振动控制,2014,34(3):15-19.

Yan Fei，Che Chidong. Analysis and Simulation of Dynamic Characteristics of Isolator Systems with Variable-stiffness Springs[J]. Noise and Vibration Control, 2014,34(3):15-19.

[4]Le T D, Ahn K K. A Vibration Isolation System in Low Frequency Excitation Region Using Negative Stiffness Structure for Vehicle Seat[J].Journal of Sound and Vibration，2011， 330： 6311-6335.

[5]Alabuzhev P,Gritchin A,Kim L,et al.Vibration Protecting and Measuring Systems with Quasi-zero Stiffness[M]. USA: Hemisphere Publishing Corporation,1989.

[6]徐道临,余奇平,周加喜,等. 准零刚度隔振系统跳跃频率区间隔振研究[J]. 中国机械工程,2014,25(2):230-235.

Xu Daolin, Yu Qiping, Zhou Jiaxi,et al. Study on Vibration Attenuation in Jumping Frequency Interval of Quasi-zero Stiffness Vibration Isolator[J]. China Mechanical Engineering,2014,25(2):230-235.

[7]Carrela A, Brennan M J, Waters T P. Static Analysis of a Passive Vibration Isolator with Quasi-zero-stiffness Characteristic[J]. J Sound Vib., 2007,301(3/5):678-689.

[8]Kovacic I, Brennan M J, Waters T P. A Study of a Nonlinear Vibration Isolator with a Quasi-zero Stiffness Characteristic[J]. J. Sound Vib., 2008, 315(3):700-711.

[9]王家胜.带附加气室空气弹簧动力学特性研究[D].南京:南京农业大学，2009.

[10]高红星，池茂儒，牛旻昊，等.空气弹簧模型研究[J].机械工程学报，2015,51(4):108-115.

Gao Hongxing,Chi Maoru,Zhu Minhao,et al. Study on Air Spring Model[J]. Journal of Mechanical Engineering, 2015,51(4):108-115.

[11]闻邦椿.机械设计手册[M].北京：机械工业出版社，2010.

[12]李吉，常凯.一种负压空气橡胶复合隔振器:中国，ZL201420194898.6[P].2014-11-05.

[13]李吉，盛国才.一种正负压隔振减振器：中国，ZL201420266224.2[P].2014-11-05.

(编辑袁兴玲)

Research on Dynamics Model and Properties of Bellows Type Vibration Isolator with Negative Pressure

Sheng GuocaiLi JiWang Jianwei

Dalian University,Dalian，Liaoning,116622

Abstract:Low frequency vibration isolator was studied herein. According to the unique features of negative pressure and the good elastic performance of rubber, a new concept of bellows type vibration isolator with negative pressure was proposed. The qualitative analyses of negative pressure isolation theory were carried out. Through mechanics modeling and theoretical simulation analyses and the experimental results indicate that the vibration isolator system has a more ideal nonlinear elastic curve. At the same time,impacts of the negative pressure and the effective area on performance were studied. Results show that, the bellows type vibration isolator with negative pressure has a strong practicability.

Key words:negative pressure; low frequency; vibration isolation；stiffness characteristic

作者简介：盛国才，男，1988年生。大连大学振动噪声研究所硕士研究生。主要研究方向为机械振动。获得专利3项。发表论文4篇。李吉，男，1959年生。大连大学振动噪声研究所所长、博士、教授。王建维(通信作者)，男，1972年生。大连大学振动噪声研究所副教授、博士。

中图分类号：TB53

DOI：10.3969/j.issn.1004-132X.2016.05.015

基金项目：国家自然科学基金资助项目(51275061)

收稿日期：2015-04-30