改进遗传算法求解TSP

张雁翔，祁育仙

(太原理工大学信息化管理与建设中心，山西太原 030024)



改进遗传算法求解TSP

张雁翔，祁育仙

(太原理工大学信息化管理与建设中心，山西太原 030024)

摘要：针对遗传算法收敛速度慢、易陷入早熟的问题提出一种改进的遗传算法。在传统遗传算法基础上，引入最近插入法产生高性能的初始种群；选择操作中加入精英保留策略，保证收敛到全局最优；根据种群进化状况自适应调整交叉概率、变异概率，克服过早收敛并加快收敛速度；在选择、交叉、变异之后加入进化逆转操作，保留亲代较多信息，增强搜索能力；提出一种新的遗传终止规则，提高遗传算法的有效性。经过国际公认的TSPLIB实验数据仿真验证，改进后的遗传算法精确性、有效性和收敛速度均有明显提高。

关键词：旅行商问题；遗传算法；最近插入法

旅行商问题(traveling salesman problem，TSP)又称为旅行推销员问题、货郎担问题，是最著名的NP完全问题。TSP并不仅仅是旅行商问题，且涉足众多领域，应用十分广泛，如邮路问题、基因组图谱绘制问题和产品的生产安排问题等，因此TSP的有效求解具有重要的意义。

目前，人工智能发展迅速，出现了许多独立于问题的智能优化算法。文献[1]讨论了蚁群算法、遗传算法、模拟退火算法、禁忌搜索算法、粒子群优化算法等求解TSP的优缺点及研究进程；文献[2]利用贪心策略指导遗传操作，提出了贪心遗传算法，保证算法的有效性；文献[3]将单亲遗传算法与模拟退火算法相结合，提高全局寻优能力。

本文对基本遗传算法(Simple Genetic Algorithm，SGA)求解TSP问题进行改进，实验结果表明，改进后的遗传算法具有较高的精确性且收敛速度快。

1基本问题描述

1.1TSP问题描述

TSP可描述为：已知n个城市以及他们相互之间的距离，求出某一旅行商经过所有城市并回到出发点的最短路线[4]。简言之，就是搜索自然子集X={1,2,…,n}(X的元素对n个城市的编号)的一个排列π(X)={V1,V2,…,Vn}，使

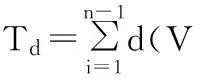
取最小值，其中d(Vi，Vi+1)表示城市Vi到城市Vi+1的距离。

1.2遗传算法描述

遗传算法(genetic algorithm，GA) 灵感来源于John Holland《自然系统与人工系统中的适应性》，其实质是模拟自然界的进化过程，将自然界适者生存规则与种群内部染色体的随机信息交换机制相结合，是高度并行、随机、自适应的全局寻优搜索算法[5]，具有很强的鲁棒性和全局搜索能力，易于其他算法相结合。目前，遗传算法已被广泛应用于组合优化、机器学习、自适应控制等领域，并取得了良好的成果。

1.3基本遗传算法求解TSP步骤

SGA是把问题参数编码为染色体，利用迭代方式进行选择、交叉、变异等操作逐步交换染色体信息，不断得到更优的群体，同时以全局并行搜索方式搜索优化群体中的最优个体，求得满足要求的最优解。其求解TSP基本步骤为：

1) 确定编码机制，初始化种群，解决TSP问题时通常采用整数编码，及使用城市序号编码，例如，1|3|5|4|2代表对于5个城市TSP问题的一个合法染色体。初始化种群采用随机法生成目标种群。

2) 计算适应度值，设n个城市的一个合法染色体为k1|k2|…|ki|kn，则该个体的适应度值为：

其中Dkikj为城市ki到kj的距离。

即此适应度函数为旅行者按照规定的路线走完所有路程的距离的倒数。优化的目标是所走路程距离最短，即该适应度函数越大，所选染色体越优质，反之越劣质。

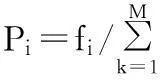
4) 交叉操作，使用单点交叉算子，任选两个体作为交叉对象，随机产生一个交叉点，两个体在交叉点互换交叉对象，采用部分映射消除冲突数字，交叉概率为Pc。

5) 变异操作，变异策略为随机选取两个点，互换位置。变异概率Pm同生物界一样，一般取值较小。

6) 迭代终止，循环进行选择、交叉、变异操作，若满足最大遗传代数则遗传终止，得出最优解。

SGA在进化前期收敛速度快，但当达到最优解的90%时，进化停滞，无法跳出局部最优，容易出现早熟收敛现象。为了提高搜索能力，克服早熟收敛，加快收敛速度，需要对算法进行改进。

2改进遗传算法

2.1最近插入法产生初始种群

GA涉及的染色体大都来源于初始种群，种群个体的质量影响全局性能，SGA随机生成初始种群，适应度值普遍偏低，算法效率低。本文采用最近插入法产生初始种群，使种群个体在初始时保持较高的适应度值，提高收敛速度。最近插入法过程如下：

1) 随机选择一个城市为当前城市，在剩余城市中选择距离当前城市最近的一个城市与之构成子路线。

2) 比较所有剩余城市到当前子路线上每一座城市的距离，选择距离子路线某一城市相距最近的一个城市插入子路线。

3) 反复操作步骤2)，最终将所有城市均插入子路线构成一个完整的路线，表示此路线的一个染色体就是种群中的一个个体。

2.2选择操作精英保留策略

在选择操作中加入精英保留策略，即在使用变异、交叉算子之前先选出适应度值最大的个体保存在最优解集中，替换子代中适应度最差的个体。目的是保留最好的个体，避免交叉、变异算子破坏其优良性，这样使得亲代的好的个体不至于由于交叉或者变异操作而丢失，子代种群中的最优个体永远不会比亲代最优的个体差。保证了种群的全局最优性。

2.3交叉、变异策略的自适应

SGA中交叉概率Pc和变异概率Pm是不变的，导致后期搜索迟钝，进化停滞，自适应控制可以有效地改善后期收敛速度，在进化过程中自适应的改变Pc、Pm的大小，将进化过程分为渐进和突变两个不同的阶段：渐进阶段强交叉、弱变异，扩大整体搜索范围，突变阶段弱交叉、强变异，使优良基因结构得以保存，且防止陷入局部最优，自适应调节公式为：

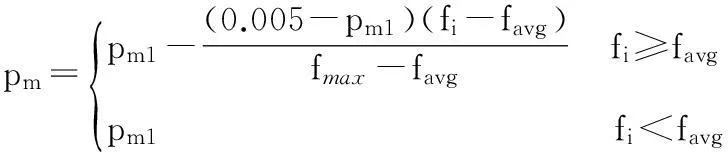
式中，fi为个体i的适应度值，favg和fmax分别为当前种群所有个体的平均适应度值和最大适应度值，pc1=0.9，pm1=0.001。

2.4进化逆转操作

TSP的关键是码串的顺序，交叉算子和变异算子会使子代维持种群的多样性，但是难以继承亲代较多的优良基因，在选择、交叉、变异之后引进进化逆转操作可以改善GA的局部搜索能力。本文的逆转算子是单方向性(朝着好的进化方向)的，只有经逆转后，适应度值有提高的才会保留下来，否则逆转无效。

例如：随机选取两个[1，9]区间内的整数r1和r2，确定两个断裂点，将两断裂点内数据进行逆转，如，r1=3，r2=7

53∣6724∣198

逆转后为：

53∣4276∣198

2.5遗传迭代终止规则

在SGA中，当迭代至最大遗传代数时迭代终止，由此得出的进化过程会由于最大遗传代数选择的不合适使进化后期进行不必要的循环迭代，出现进化停滞。为了避免此现象，本文提出一种新的终止规则。

本文规定，若连续Q代内都满足条件|fgmax-f(g-1)max|≤ε，其中ε为适当小的正数，fgmax为第g代种群内个体的最大适应度值，f(g-1)max为第g-1代种群内个体的最大适应度值。

2.6改进遗传算法基本流程

改进后遗传算法求解TSP流程图如图1所示。基本流程为：

Step1：种群初始化；

Step2：对种群各个体进行适应度值计算，循环进行选择、交叉、变异和进化逆转操作，直至达到终止条件。

图1　改进遗传算法流程图

选择算子：采用随机遍历抽样选择，选择时采用随机等距的方式选择个体。

交叉算子：采用部分映射杂交，根据当前进化情况自适应调整交叉概率。

变异算子：随机选取两个点，将其对换位置。根据当前进化情况自适应调整变异概率。

3实验结果及分析

本文采用MATLAB语言对改进遗传算法设计实现。并用TSP样本案例库TSPLIB中的部分数据进行仿真分析。实验环境为：windows 7系统，2G内存，Matlab R2010b平台。

分别使用改进GA和SGA对国际公认的TSPLIB实验数据仿真验证后，得出实验结果对比如表1，可以得出，改进后的遗传算法相对于SGA不仅可以搜索到最优解，而且收敛到最优解的速度也较快，有效性高，SGA容易陷入局部最优，如pr136。

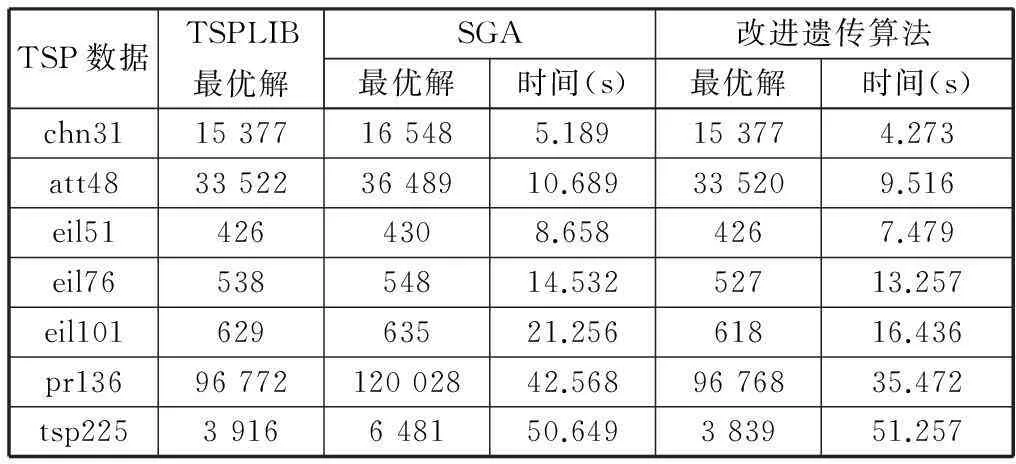
表1　实验结果对比分析

改进的GA可以产生高性能的初始种群，且可以在较短的代数内收敛至全局最优，当进化停滞时，新的终止条件可以避免算法进行无效的进化，提高有效性，如图2所示。

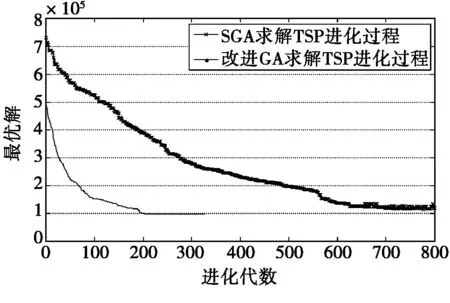
图2　pr136改进GA和SGA进化曲线

采用改进GA对TSPLIB中部分数据进行仿真得出各数据最优路线图如图3至图5。

图3　chn31最优路线轨迹图

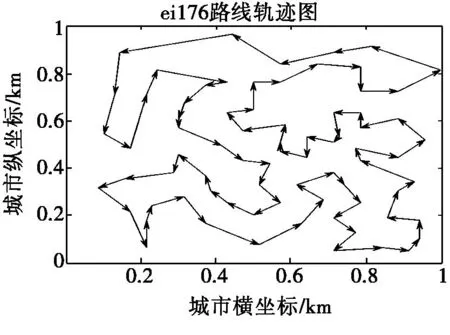
图4　eil76最优路线轨迹图

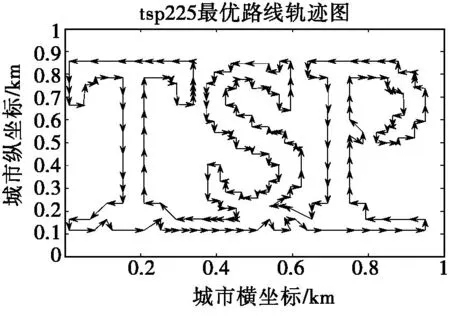
图5　tsp225最优路线轨迹图

4结束语

本文对传统的遗传算法进行了改进，使用最近插入法生成部分初始种群；加入精英保留策略，自适应调整交叉、变异概率，加入了进化逆转算子；提出了一种新的遗传终止条件。通过实验仿真显示，改进遗传算法在搜索最优能力、有效性和收敛速度方面都有明显的提高。

参考文献

[1]高海昌，冯博琴，朱利.智能优化算法求解TSP问题[J].控制与决策,2006,21(3):241-247.

[2]魏英姿，赵明扬，黄雪梅，等.求解TS问题的贪心遗传算法[J].计算机工程,2004,30(19):19-20.

[3]曹恒智，余先川.单亲遗传模拟退火及在组合优化问题中的应用[J].北京邮电大学学报,2008,31(3):38-41.

[4]William J,Cook.Traveling Salesman:Mathematics at the Limits of Computation[M].隋春宁,译.北京:人民邮电出版社,2013:10.

[5]刘荷花，崔超，陈晶.一种改进的遗传算法求解旅行商问题[D].北京理工大学学报,2013,33(4):390-393.

An Improved Genetic Algorithm for Solving TSP

Zhang Yanxiang, Qi Yuxian

(CenterofInformationManagementandDevelopment,TaiyuanUniversityofTechnology,TaiyuanShanxi030024,China)

Abstract:For the problem of slow convergence speed and easy to fall into precocity with genetic algorithm, an improved genetic algorithm is proposed. Based on simple genetic algorithm, the paper obtains the high-performance initial population with nearest insertion heuristic algorithm, introduces elitism in selection operation to globally optimal solution, adjusts the crossover and mutation probability adaptively according to the evolution situation to overcome the premature convergence and accelerate the convergence speed, performs the reverse evolution after selection, crosser and mutation operation which can keep more parental information and enhance search capabilities. A new genetic termination rules is built in order to increase the effectiveness of genetic algorithm. Through the TSPLIB experimental data simulation, the improved genetic algorithm is improved obviously on accuracy, validity and convergence speed.

Key words:travelling salesman problem (TSP); genetic algorithm; nearest insertion

中图分类号：TP183

文献标识码：A

文章编号：1674- 4578(2016)01- 0028- 03

作者简介：张雁翔(1976- )，女，山西长治人，工程师，硕士。

收稿日期：2015-10-29