一种具有任意负载的有损传输线瞬态响应分析方法
曹彦玲
(合阳县职业技术教育中心,陕西 渭南 715300)
一种具有任意负载的有损传输线瞬态响应分析方法
曹彦玲
(合阳县职业技术教育中心,陕西 渭南 715300)
摘要:精细积分法是一种有效的传输线瞬态响应时域分析方法,针对精细积分法难以处理具有电抗性质负载的缺陷,本文提出了一种新的传输线瞬态响应分析方法。该方法通过对精细积分法所建立的一阶微分方程的强制项按一定的规则进行分解,并引入元件的伴随模型,使精细积分法能够分析具有任意性质负载的传输线瞬态响应问题,极大地提高了精细积分法分析传输线瞬态响应的功效。
关键词:有损传输线;时域响应;任意负载;精细积分法
时域法与频域方法是传输线瞬态响应分析常用的两种方法。时域法直接,便于分析非线性负载,但却难以分析具有电抗性质的负载;频域法虽然分析具有电抗性质的负载相对比较容易,但难以分析非线性负载[1]。在高速VLSI中,不仅具有大量的非线性电子器件,还会有电容性、电感性等各种性质的负载。因此,研究具有任意负载的传输线瞬态响应分析方法,具有重要的意义。
文献[2]在传输线瞬态响应分析中提出的精细积分法,是一种时域分析方法。该方法能够很容易地处理传输线非零初始值及非线性负载等问题,但却难以处理具有电抗性质的负载问题。本文通过引入电容及非线性负载等的时域伴随模型,并对精细积分法所建立的一阶微分方程的强制项进行分析,将传输线的始端及终端条件加以分离,成功地解决了精细积分法难以处理具有任意性质负载的传输线瞬态响应分析问题,极大地提高了精细积分法分析传输线瞬态响应问题的功效。
1对精细积分法的改进
对电报方程

(1)
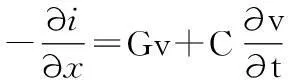
(2)
式中,v=v(x,t),i=i(x,t),D为传输线的长度。对空间坐标x进行离散,得

(3)

(4)
式中,Δx=D/M,ik=i(kΔx,t),vk=v(kΔx,t),k=0,1,2,…M。将(3)、(4)式写成矩阵形式即为:

(5)
式中
X=(v1v2…vMi0i1…iM-1)T
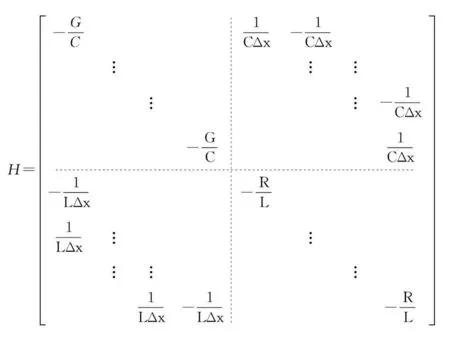
F=[0…0(CΔx)-1i0M(LΔx)-1v00…0]T.
(6)
传输线的边界条件可表示为:
v(0,t)=f1[i(0,t),vs(t)] .
(7)
v(l,t)=f2[i(l,t)] .
(8)
对于传输线,在极小的时间范围(tj,tj+1)内,首末端的电流
i0(t)≈i0(tj)、iM(t)≈iM(tj)t∈tj,tj+1.
(9)
于是,在时间范围(tj,tj+1)内,可以认为v0(t)仅是激励vs(t)的函数,而iM(t)为已知数。
由此将(6)式改写为:
F=F1+F2.
(10)
式中
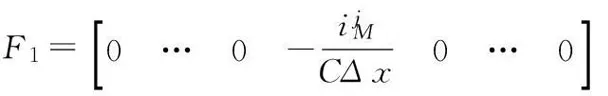

将(10)式代入(5)得
X(tj+1)≈exp(Hτ)X(tj)+H-1[exp(Hτ)-1]F1(tj)+

(11)
式中,tj=jτ,j=0,1,2,…,τ,为时间步长。
对于(11)式中的F2项,在t∈(tj,tj+1)时刻,只有vs是时间的函数。而在目前常用的信号中,其大部分可以表示为初等函数或初等函数的组合,(11)式中的积分项是可以直接积分的,并表示成EXP(Hτ)的函数。而F1项与负载在tj时刻负载的电流值有关。因此,(11)式最终归结为EXP(Hτ)的计算,EXP(Hτ)的计算详见文献[7]。
2算例
传输线系统如图1所示,传输线参数为:
R=0.1 Ω/m,G=0.1 nS/m,L=250 nH/m,C=100 pF/m
负载电容Cd=10 pF,非线性电阻的伏安特性为i=10(e40v-1)nA。

图1 传输线系统模型
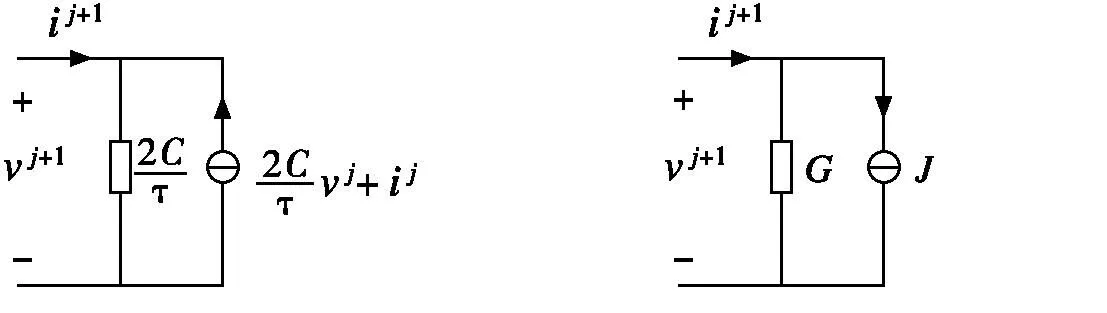
图2电容元件的伴随模型图3非线性压控型元件的伴随模型

取M=50,τ=2ps,传输线终端电压vo的瞬态响应波形如图4所示。由图可见,经过一段时间延迟之后,终端电压vo迅速上升到最大值并持续一段时间。此后,随着输入的减小,vo经过一定的过程趋于零,vo的上升时间小于下降时间,与定性分析基本吻合。
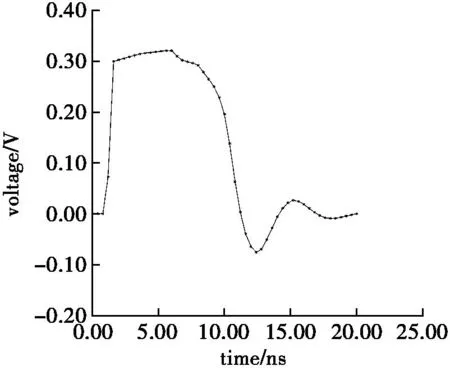
图4 传输线终端电压响应
3结论
通过对精细积分法所建立的一阶微分方程的强制项进行分解,并引入元器件的伴随模型,使精细积分法在传输线瞬态响应分析中,不仅能够分析具有电抗性质的负载,还可以分析具有任意性质的负载,极大地丰富了精细积分法分析传输线瞬态响应的功效。
参考文献
[1]AntonijeR,Djordjevic,TapanK,etal.AnalysisofLossyTransmissionLineswithArbitraryNonlinearTerminalNetworks[J].IEEETrans,MTT,1986,34(6):660-665.
[2]赵进全,马西奎,邱关源.有损传输线时域响应分析中的精细积分法[J].微电子学,1997,27(3):181-185.
[3]钟万勰.暂态历程的精细计算方法[J].计算结构力学及其应用,1995,12(1):1-6.
[4]任艮,甘叔贞.电路的计算机辅助分析与设计[M].北京:北京理工大学出版社,1989.
[5]TakaoKomuro.Time-DomainAnalysisofLossyTransmissionLineswithArbitraryTerminalNetworks[J].IEEETrans,CAS,1991,38(10):1160-1164.
Analysis Method of the Transient Response of Lossy Transmission Lines with Arbitrary Loads
Cao Yanling
(HeyangVocationalandTechnicalEducationCenter,WeinanShaanxi715300,China)
Abstract:The precise integration method is an effective method to analyze the transient response of transmission lines, but this method is difficult to analyze the transient response of transmission lines with the reactive loads, so a new analysis method of transient response of transmission lines is proposed. By decomposing the forced term of first-order differential equations which is established by the precise integration method according to certain rule, and adopting the companion models of components, the transient response of transmission lines with arbitrary loads can be analyzed by the improved precise integration method, and the efficacy of the precise integration method to analyze the transient response of transmission lines is improved greatly.
Key words:lossy transmission lines; time-domain response; arbitrary loads; the precise integration method
中图分类号:TN402
文献标识码:A
文章编号:1674- 4578(2016)01- 0011- 02
作者简介:曹彦玲(1985- ),女,陕西合阳人,合阳县职业技术教育中心二级教师,主要从事物理及电子技术教学研究。
收稿日期:2015-09-28

