基于OSEM算法的冲击波超压场重建技术

王　凤，白原齐

(中北大学，山西 太原 030051)



基于OSEM算法的冲击波超压场重建技术

王凤，白原齐

(中北大学，山西 太原 030051)

摘要：利用走时层析成像方法重建水中爆炸冲击波超压场，结合冲击波传输特性来反演速度场完成冲击波超压场的重建。试验中爆炸点和传感器数目不足给重建过程带来困难，于是文中提出了一种基于先验信息的OSEM反演算法。首先建立数学模型，再运用MATLAB进行仿真实验，最后对仿真结果进行分析。实验表明，本文方案相比传统重建方法迭代次数更少、重建精度更高。说明该算法能有效解算这种欠定重建问题。在实际爆炸中实用性较高，可指导野外施工。

关键词：走时层析成像；水中爆炸；超压场重建

水下爆炸是毁伤舰船、潜艇以及大型鱼雷等水中航行器的一条重要途径，对舰船目标在水下爆炸作用下毁伤效应的研究历来受到各海洋强国的重视。对水中爆炸冲击波超压场重建的研究在评估水中爆炸的威力、控制爆炸的危害等爆炸安全技术方面意义重大[1，2]。

目前我们一般用水下压力传感器进行试验，测量出相应的冲击波超压，由于该类传感器防水性好、稳定性好、对系统响应频率高等，而能满足这种要求的压力传感器价格昂贵，为实际试验增加了成本费用。试验所用的传感器价格昂贵，传感器数目越少，试验成本越低，传感器数目越多，反演精度越高，同时试验成本也越高。

本文采用走时层析的方法重建水中爆炸超压场，此类工程问题必然导致重建数据的不完全。运用合适的迭代重建算法，使得可用最少数目的传感器重建最高精度的冲击波超压场。

针对这种不完全数据重建问题，在算法研究方面，被提出了一些实用的迭代重建的算法及它们的改进算法，如SIRT算法、SART算法[4，5]等，这两种算法能在一定程度上提高重建精度。但其重建速度很慢。由于在实际爆炸工程应用中，传感器布局及测量误差导致数据不完整，使得反演算法的不稳定性和误差大大增加。本文提出了一种基于先验信息的OSEM反演算法，来解决这种不完全数据走时的欠定问题。

1冲击波超压场重建方案

水中爆炸冲击波峰值超压场重建通过三个步骤，第一步对各个传感器阵元采集获得的冲击波信号进行分析及特征提取，得到冲击波到达时间，在这里定义为走时，第二步采用走时层析成像[6-8]方法重建待测区域内的冲击波速度，第三步根据速度与冲击波峰值超压的关系，最后将网格的速度值运用相应公式转换成超压值，来重建出整个二维平面上的冲击波超压值。

根据冲击波的传输特性，将重建区域划分成规则网格。本文中假设一条射线对应一个传感器并假设冲击波不是沿网格单元的边界传播。定义冲击波从激励源到达探测器的时间为走时，综上可得冲击波在传输的过程中，其走时是速度和几何路径的函数，如式(1)所示：

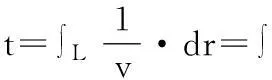
(1)

式中，r为射线；v为速度；s为慢度；L为积分路径。 将上式离散化，根据测试区域网格划分情况，对于第i条射线有：

(2)

式中，ti为第i条射线的走时，即冲击波波阵面到达传感器的时间；dij为第i条射线穿过第j个网格的射线长度；sj为第j个网格中的慢度；M为射线数；N为网格数。

将上式(2)写成矩阵形式为：

DS=T.

(3)

其中，P=(p1，p2，…，pM)′为各条射线走时的M维列向量；X=(x1，x2，…，xN)′为待求离散单元慢度值，为N维未知的列向量；D为M×N阶稀疏矩阵，其元素为dij。

矩阵方程组(3)中，因为每个网格单元只有一少部分射线穿过，所以得到的方程式中的矩阵D是一个大型的稀疏矩阵，该矩阵中非零元素比例很大，它的不完全投影使得问题欠定，同时测量过程存在一定的误差，这些误差决定了不相容性。方程组(3)采用OSEM算法求解。能有效改善该问题。

2重建算法及重建误差

2.1联合迭代算法SIRT

联合迭代重建算法SIRT，是比较常用的迭代重建算法。其公式为：

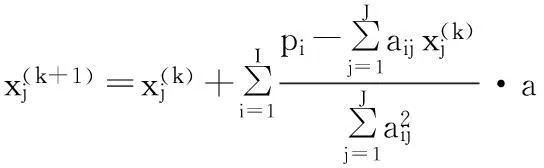
(4)

迭代步骤分为：对向量x赋初值x=x(0)。

修正x=x(k)(k=0,1,2,…)：

1) 投影：

(5)

即计算射线1到射线I的线积分估计值。

2) 反投影：计算第j个体素的修正值，按体素进行逐个修正

(6)

每迭代一轮，方程组更新一次。

3) 重复2)，xk收敛时停止。

2.2联合代数重建算法SART

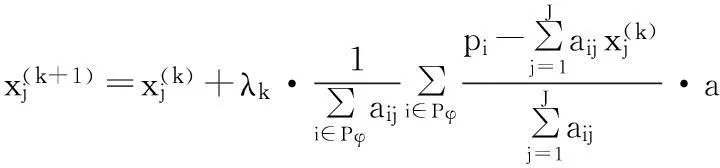
(7)

其中，λ是0<λ<2的一个松弛因子。

具体步骤为：

1) 对图像向量x赋初值x=x(0)；

2) 选择投影方向。对x=x(k)(k=0,1,2,…)进行修正：

第一步，投影：计算该投影方向角度下的所有射线的线积分估计值，

(8)

第二步，反投影：计算J各提体素的修正值，按体素进行逐个修正

(9)

循环到完成一轮迭代。

2.3重建误差

如下为第i个网格单元的速度相对误差：

(10)

其中，v′j为真实值，vj为重建的速度值。

定义网格平均相对误差为：

(11)

速度最大相对误差

(12)

定义第i条射线走时相对误差为：

(13)

相应地走时平均相对误差：

(14)

从而得到走时最大相对误差为：

(15)

3OSEM重建算法

为了加快收敛速度，减少运算时间，提高重建精度，人们提出了很多快速算法，有序子集最大期望值法是很有应用前景的一种快速迭代重建算法，它是在最大似然期望法(Maximum Likelihood Expext at ion-max-imization，ML-EM)的基础上发展起来的。传统的ML-EM方法计算式为：

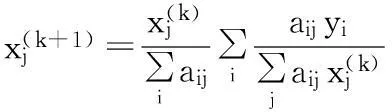
(16)

设定重建图像大小为n×n，360个投影角度，每个角度下n条投影射线。将投影数据按投影角度划分成T个有序子集。 OSEM算法的迭代公式如下：Sl表示第l个子集，l=1,2,…,T。

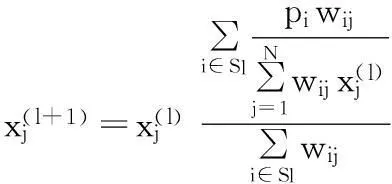
(17)

3.1建立数学模型

建立仿真模型是一个自由介质的冲击波速度分布模型，假设根据冲击波传输特性重建区域均匀对称，所以取四分之一区域研究。如图1所示，激励源位于重建区域中心位置，探测器遍布于整个边界并且尽可能多方位覆盖被测区域。先把该区域划分为5×5的网格单元，使它的分辨率为1 m，传感器分布在爆炸点的下边界和左边界，本文用到了13个传感器放在边界，多余的传感器放置在内部，用来采集信息作为先验信息。

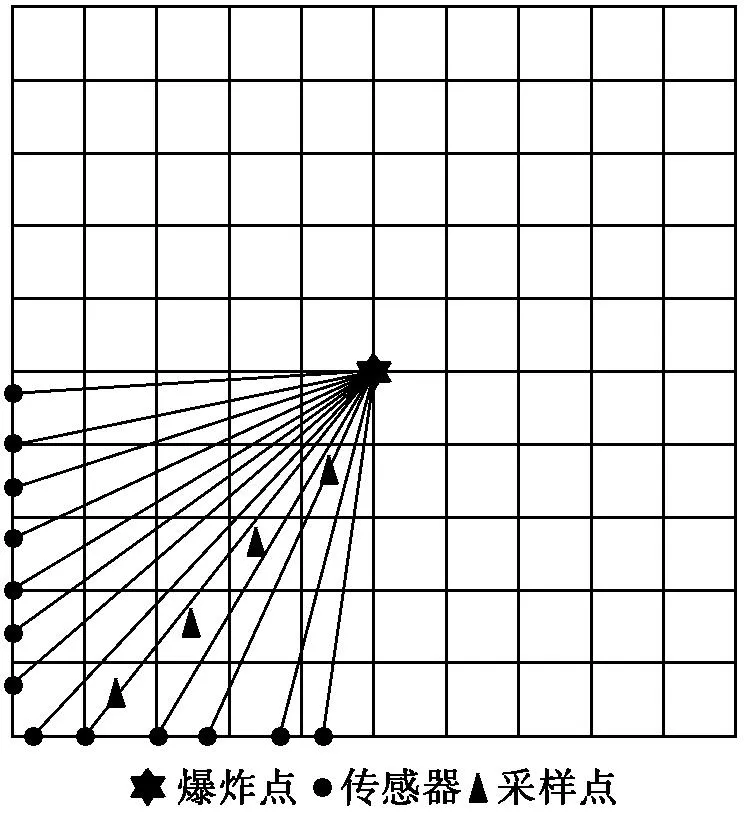
图1　重建区域网格均匀离散图

3.2仿真结果及分析

基于以上模型参数，下面主要从平均误差和计算速率(迭代次数)两个方面来分析。

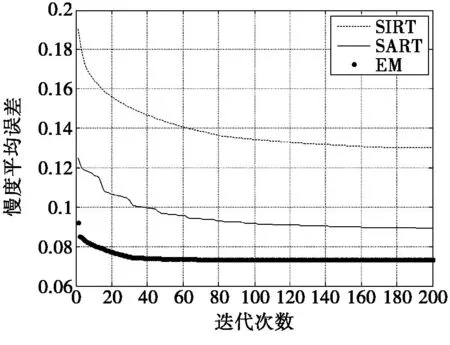
(a) 慢度平均误差与迭代次数的变化关系

(b) 慢度最大误差与迭代次数变化关系

(a) 理想假设模型

(b) SIRT算法重建结果

(c) SART算法重建结果

(d) OSEM算法重建结果

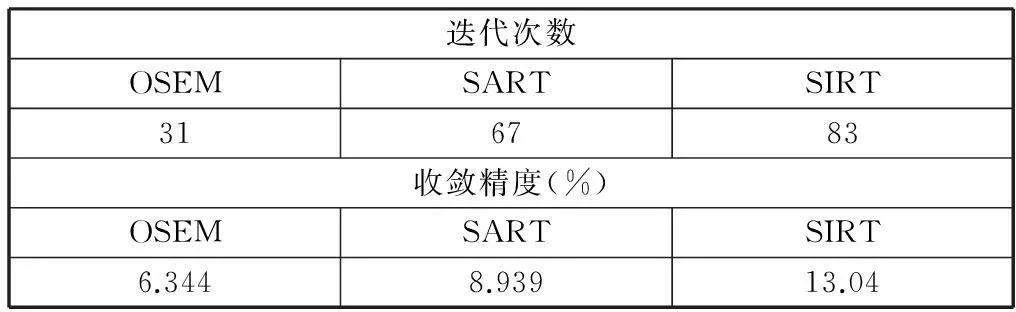
迭代次数OSEMSARTSIRT316783收敛精度(%)OSEMSARTSIRT6.3448.93913.04

通过以上分析可知：在冲击波场重建中，创痛算法和本文算法的精度的变化趋势都达到稳定趋势，OSEM算法的迭代次数最少，即该算法的重建速度最快；OSEM算法的收敛精度最高，即用该算法重建误差最小。所以本文选用OSEM算法以最高的精度和最快的速度解决欠定问题。

3.3对OSEM算法进行改进

本文通过加入先验信息，即采集重建区域内部传感器的信息作为先验信息，重建爆炸场。一般先验信息有三种: 第一种是能得模型参数大概分布特点；第二种是由先验认识得部分参数的一定取值范围；第三种是能获得少部分参数的精确值。这里采用第三种，直接把采集到的信息作为特定参数的精确值，将其加入到方程(3)。实际试验应用中，我们把反演区域进行个别点取样，然后测得该位置波速作为第3种先验信息，相当于在线性方程式(3)下增加约束方程组

WS=S′ .

(18)

式中，W为k×n维矩阵，k为被约束的参数个数，且wi=[000…100]，设被约束参数的位置为1，其他为0。s′为采样点测出的观测值，于是式(3)改为：

(19)

式中，D0是无样点先验信息的距离矩阵，T0是走时矩阵。将上式改写为DS=T再进行计算。

3.3.1仿真结果及分析

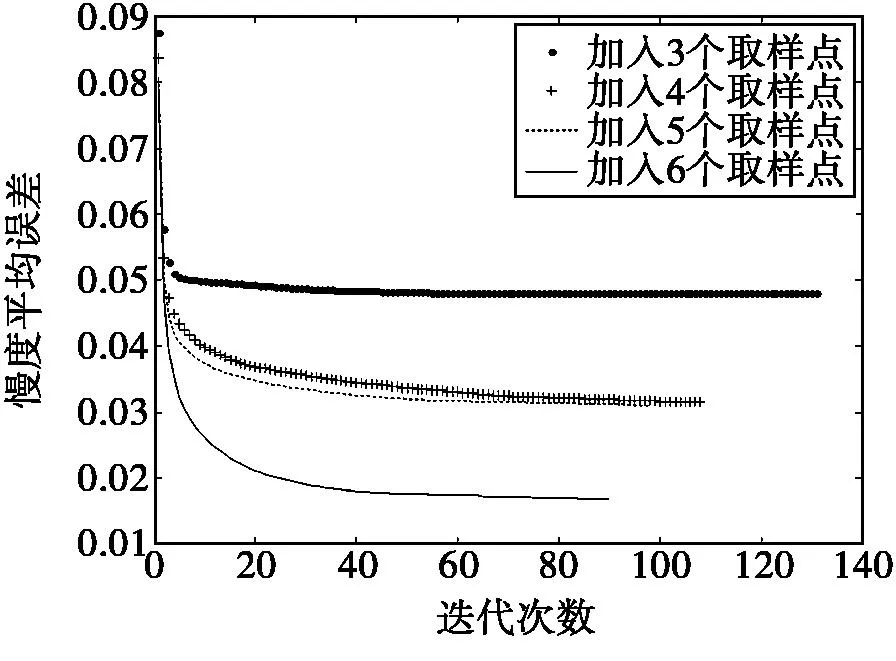
图4　本文方法的重建平均误差的变化

图5　本文方法的各网格绝对误差

图6　本文方法的OSEM算法重建结果

由图4、图5可知，随着采样点由3个增加到第6个，反演误差逐渐减小。加入3个先验值时反演误差接近5%，加入4个先验值时和再加一个是误差变化不大，都接近3%，加入6个先验值时误差减小到低于2%。

综上所述，表明采样点的增加伴随着重建误差的减小，但并表明采样点数越多实验精度越大，因此本文的方案可以明显地提高算法精度。但是采样点数的增加意味着传感器数目的增加，而水下传感器成本高试验费用大。实际试验中需要综合考虑。图6显示了基于先验信息的OSEM算法重建结果，相比前面介绍的方法要更接近理论模型。

4结论

本文针对爆炸中不完全数据的超压场重建问题，提出了一种基于先验信息的OSEM反演算法。设定初始模型后经过MATLAB对该算法仿真，主要分析反演误差和迭代次数两个方面，即得到反演精度和反演速率。OSEM算法在解这种不完全数据的欠定问题中的误差较小。对此算法进行改进，即加入采样点作为第三种先验信息，发现加入先验值后的重建算法速度更快精度更高。

OSEM算法相对较稳定，试验表明该方法可以获得比较好的反演结果。但总的来说它的计算速度比较慢，并且需要加较大的存储空间。本文的研究结果为在单一激励源层析成像中根据要求的精度和运算速度选择反演算法提供了有用的参考。

参考文献

[1]叶序双，顾文彬，刘文华，等.水下爆炸研究现状[J].工程爆破,1999,5(1):84-87.

[2]李磊，冯顺山.水下爆炸对舰船结构毁伤效应的研究现状与展望[J].舰船科学技术,2008,30(3):26-30.

[3]Snay H G.The Scaling of Underwater Explosion Phenomena[R].AD-271468,Jun.1961.

[4]Charles L.Byrne.Applied Iterative Methods[M].A K Peters/CRC Press,2007.

[5]Tanabe K.Projection Method for Solving a Singular System of linear Equation and ITS Applications[J].Numer Math，1971,17:203-214.

[6]王家映.地球物理反演理论[M].北京:高等教育出版社,2011.

[7]GUO Cheng-hao,Liu Feng-yu.Model and Analysis of Adaptive Grid Computing[J].Computer Engineering,2008,34(8):117-119.

[8]黄靓.混凝土超声层析成像的理论方法和实验研究[D].湖南:湖南大学,2008.

Reconstruction Technology of Blast Wave Overpressure Field on OSEM Algorithm

Wang Feng, Bai Yuanqi

(NorthuniversityofChina,TaiyuanShanxi030051,China)

Abstract:In this paper, the technique of blast wave field reconstruction based on tomography is studied. Overpressure field is reconstructed by inverting the velocity field in the process of shock wave transmission. Since the reconstruction process is difficult due to insufficient excitation sources and detectors, an OSEM algorithm is proposed based on priori information. Appropriate models are constructed using the proposed methods, and a simulation example is put forward at last. The result reveals that compared with the traditional methods, this method has higher precision and converges faster. It also shows the validity and practicality of the developed algorithm in solving the problem of incomplete data reconstruction.

Key words:traveltime tomography; underwater explosions; reconstruction of overpressure field

中图分类号：TP301.6

文献标识码：A

文章编号：1674- 4578(2016)01- 0015- 04

作者简介：王凤(1990- )，女，湖北仙桃人，硕士研究生，主要从事信号处理、重建类算法。

收稿日期：2015-10-09