绳-船模型的教学研究



绳-船模型的教学研究

摘 要：绳-船模型是典型的运动学问题，已见的解答存在令人费解之处．本文细致探究了绳-船模型的解法，结果表明：有3种可行的中学物理方法、2种基本的大学物理方法；讨论了解决绳-船模型的疑惑，提出了相应的教学建议．

关键词：绳-船模型物理过程物理概念物理方法

1引言

绳-船模型是典型的运动学问题.如图1，岸上某人用绕过定滑轮的不可伸长的(轻)绳以匀速v0拉湖面上连接绳的小船靠岸，当绳与水平面成角θ时，小船的速度有多大？

常见的流行解析为：船(或连接船的绳端)的运动为合运动，分解为沿绳方向和垂直绳方向的分运动，于是得船速大小为

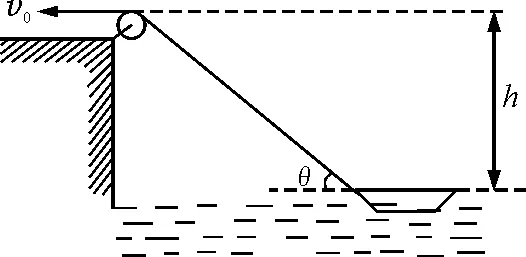
图1　绳-船模型

然而，绳-船模型的解析均基于似乎凭想象确认的船(或连接船的绳端)的运动效果——沿绳方向收缩、绕定滑轮转动[1~4]，难免令人费解．如何从物理理论论证船的运动效果？对绳-船模型，有哪些合理的解法？怎样从物理学方法论层次理解？本文就此进行相应的探究，以期释疑解惑、明晰绳-船模型的物理实质，并为其开放式教学设计奠定基础．

2解法探究

2.1中学物理解法

2.1.1微元法

如图2，斜绳与定滑轮相切处O为参考点，经时间Δt，船沿湖面由A点运动到B点，位移矢量为Δr，取OC=OB，则船的位移矢量三角形为△ABC；Δt足够短或趋于零时，分位移Δr2垂直于分位移Δr1；因此，船的运动自然而然是沿绳的分运动、垂直绳的分运动的合运动．Δt足够短或趋于零时，由图2的三角函数关系得

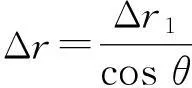
(1)

Δr2=Δr1tanθ

(2)

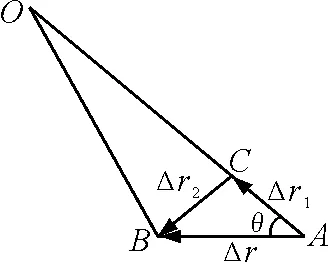
图2　船的位移关系

依据瞬时速度概念有

(3)

(4)

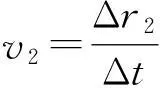
(5)

v的方向水平向左，v1的方向沿绳向上，v2的方向垂直绳向下，如图3所示．依题意：绳收缩，则由式(4)得

v1=v0

(6)

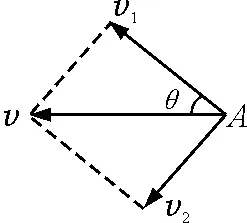
图3　船的速度关系

由式(1)～(6)得

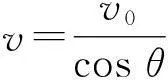
(7)

v2=v0tanθ

(8)

式(6)、(7)、(8)分别是船的分速度v1，合速度v，分速度v2的大小的表达式．

由图2的位移矢量图可形象理解为什么船速v大于绳速v1——Δt足够短或趋于零时，直角△ABC的斜边Δr大于直角边Δr1，从而有式(1)、(3)、(4)、(6)；或由速度矢量图3形象理解之——分速度v1与v2垂直，合速度v大于分速度v1(“大于”指大小关系)．

2.1.2合成法

由图2的位移矢量△ABC知：Δt足够短或趋于零时，船的运动是沿绳的分运动、垂直绳的分运动的合运动；相应地，船的速度v是沿绳收缩的速度v1，绕O转动的速度v2的合速度，速度矢量图如图3；由题意v1=v0，结合图3的三角函数关系可得式(7)、(8)．

虽然矢量的分解与合成互逆，但此处的问题是知分速度v0的大小、方向，求合速度v的大小(方向已知，沿水平向左)，这是速度的合成；因此，称为合成法更合乎物理逻辑．

2.1.3能量(守恒)法

不计定滑轮的质量、滑轮与轴间的摩擦、绳的质量，则在人用绕过定滑轮的绳拉船的过程中，绳拉船做的功应等于人拉绳做的功(即人输出的能量)；因绳、船连动，则绳拉船的功率等于人拉绳的功率，即[2]

P绳=P人

(9)

而

P绳=Fvcosθ

(10)

P人=Fv0

(11)

式中F为绳拉船的力的大小，等于人拉绳的力的大小(均等于绳的弹力大小)；由式(9)～(11)可得式(7)．

由式(9)～(11)可理解为什么船速v大于绳速v0．绳拉船时，绳的拉力与船速有不为零的夹角，为使绳拉船的功率P绳等于人拉绳的功率P人，必使船速v大于人拉绳的速度v0．

2.2大学物理解法

2.2.1直角坐标分量法

湖岸为参考系，斜绳与定滑轮相切处为原点O，建立平面直角坐标系O-xy，如图4所示.

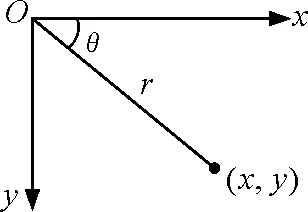
图4　船的直角坐标

将船作为研究对象，视作质点，位置坐标为(x,y)，位置矢量为

r=xi+yj

(12)

式中r，x均是时间t的变量，而y=h为恒量(因船沿湖面水平向左运动)；则船的速度为

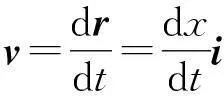
(13)

由图4的几何关系，有

x2=r2-y2

(14)

对t求导，得

(15)

依题意,绳缩短，则有

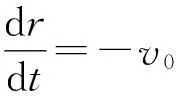
(16)

由式(13)、(15)、(16)得

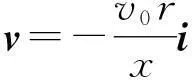
(17)

再由式(14)～(17)得船的加速度[5]

(18)

式(17)、(18)由图4的几何关系可表示为

(19)

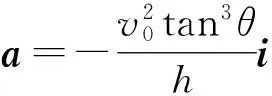
(20)

式(17)、(18)或(19)、(20)表明：船的速度、加速度的方向均沿x轴反向．

2.2.2直角坐标参量法

参考系、坐标系同前，如图4，取r与θ为参量，则船的位置坐标可表示为

x=rcosθ

(21)

y=rsinθ

(22)

式中x,r,θ均是时间t的变量，而y=h为恒量(因船湖面沿水平向左运动)；求导得

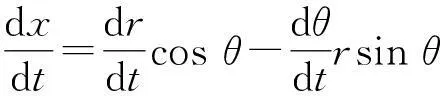
(23)

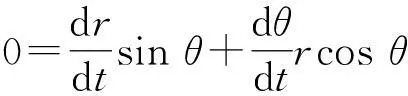
(24)

由式(23)、(24)和同理的式(16)得

(25)

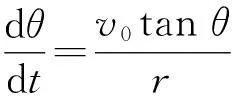
(26)

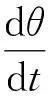
再由式(25)、(26)得船的加速度

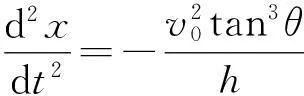
(27)

式(25)、(27)中的负号表明：船的速度、加速度的方向均沿x轴反向．

3疑惑讨论

3.1如何理解船的合运动

绳-船模型的研究对象是船，应依据瞬时速度概念求船的速度；而从运动学求解速度的基本方法之一是基于位移，这就自然、合理地要考察船的位移Δr；而求解Δr必然要与题设已知的绳速关联，即与绳缩短的位移Δr1关联；因绳、船连动，则有图2所示的船的位移矢量三角形就成为使然．Δt足够短或趋于零时，则有图3所示的船的速度矢量图．这样就从物理概念(位移、速度)论证了船的运动是沿绳的分运动和垂直绳的分运动的合运动．参见图2，Δt足够短或趋于零时，可将船的位移Δr等效为相对于参考点O的位置矢量r(图2中未画出)的大小变化即分位移Δr1[引起分速度v1，参见式(6)]和方向变化即分位移Δr2[引起分速度v2，参见式(8)]．这样就从等效观自然而然地论证了船的运动是沿绳方向的分运动和垂直绳方向的分运动(即先由A点到C点的分运动v1、再由C点到B点的分运动v2)的合运动．

3.2能否观察到船的分运动

试图用平面极坐标解释船的运动效果为沿绳运动、垂直绳转动，并预言能实际观察到这两个效果[3]，进而说明有图3所示的“速度分解”．这似乎是靠想象、凭经验的结论．

平面极坐标系为动坐标系，即坐标单位矢量r，θ是变矢量；而平面直角坐标系为恒坐标系，即坐标单位矢量i与j为恒矢量；用平面极坐标解决绳-船模型无形之中提高了要求--需确定坐标单位矢量的时间导数[6]．因此，绳-船模型的解决，从大学物理考虑，用平面直角坐标较简捷．

3.3船的分运动的合成结果

图3所示的垂直绳的分运动v2可能引起学生的疑惑(既然有分运动v2，船为什么没有向下运动或潜入水下？)，为此，按图5将v1，v2分别沿竖直、水平方向分解得

图5　船的分运动的分解

v3=v1sinθ

(28)

v4=v2cosθ

(29)

v=v1cosθ+v2sinθ

(30)

由式(28)、(6)和式(29)、(8)得

v3=v0sinθ

(31)

v4=v0sinθ

(32)

由式(30)、(6)、(8)可得式(7)．

式(31)、(32)表明：分运动v1，v2合成的结果是竖直方向的运动效果彼此抵消、仅有水平向左的运动效果，即船的可实际观察到的运动．学生若能认识到船的分运动的合成结果，则其心中的疑惑(如有分运动v1，船怎么没有竖直向上运动？有分运动v2，船怎么没有竖直向下运动？)便可迎刃而解．

3.4涉及的物理方法

就中学物理而言，绳-船模型考查的是物理概念(位移，速度)、物理方法(微元法、合成法，能量法，等效法)；因此，从物理方法(特别是等效法)层次理解绳-船模型显得尤为必要．

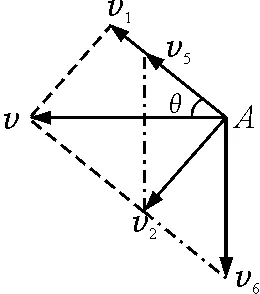
图6

将图3的分速度v2分别沿绳方向、竖直方向分解，得分速度v5，v6，如图6；再将分速度v1，v5合成得v7，至此船的合运动v等效为分运动v6，v7，如图7.

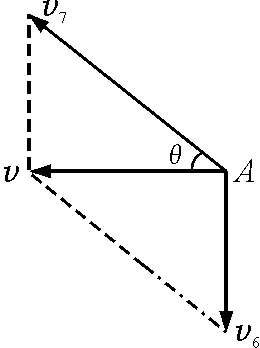
图7

相应速度大小关系为

v5=v2tanθ

(33)

(34)

v7=v1+v5

(35)

再结合式(6)、(8)得

v5=v0tan2θ

(36)

(37)

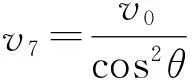
(38)

由式(37)、(38)和图7可进一步检验分运动v6，v7的合运动的确是船的运动v，即式(7)．这就推证了分运动v6，v7与分运动v1，v2等效，且与合运动v等效．事实上，不同形式的分运动，不仅相互等效，而且与合运动等效；但就绳-船模型而言，基本形式的分运动是图3所示的v1，v2．

比较上述绳-船模型的解法知，微元法、合成法是运动学的基本方法，但合成法以微元法为基础；能量法是后续的基本方法；导数法是物理概念与数学工具相结合的严密方法，但目前高中物理尚未要求、仍可尝试(待学习了高中数学的导数内容后，大学物理中导数法是解决运动学问题的基本方法)．因此，微元法、合成法、能量法是目前解决绳-船模型的高中物理基本方法．

由上述讨论知，依据物理概念达到物理方法的层次，方能对绳-船模型理解到位，可使问题的解决有根有据、逻辑严谨、层层递进、步步深入；因此，若达此水平，不仅知其然而且知其所以然，即便是中学物理与大学物理间的“边缘试题”或“擦边球试题”[3]，也能依据相关物理概念、规律、方法基本解决，而不再依赖某种“经验”或“套路”．

4教学建议

基于上述解法、讨论，提出以下参考性教学理念、教学策略的建议．

4.1教学理念

学生解决绳-船模型的两种典型错解[4]表明：学生出错是凭感觉、想当然，或受运动的合成与分解的思维定势的驱使，或思维片面性所导致；而有些教师对此问题的讲解似乎是凭经验、重结果、凑答案[4]，难免“美中不足”或有点遗憾．由上述解法、讨论知，认清船或连接船的绳端的运动过程是解决问题的基础，合理运用相关物理概念、物理方法是解决问题的关键；因此，回归物理过程、物理概念、物理方法是解决绳-船模型的教学基本理念．

4.2教学策略

虽然就绳-船模型的教学提出了针对学生两种典型错解的顺学而导、补全原解的策略，并进行了有益的教学实践尝试[4]；但此策略主要是顺着学生错解的思路、教师点拨引导、学生达到正解、学生对比反思，并未深究学生错解的思维起点(两错解的思维起点分别是：分解绳速，误认为绳速沿水平方向的分速度等于船速；分解船速，误认为船速沿绳方向的分速度等于绳速)，学生的反思也未必能理解绳端的运动效果(因为教师的引导基于运动过程的想象，未进行严谨的物理理论推证)．

基于上述教学理念，若按学生尝试→教师讲解→师生对话的教学过程解决绳-船模型，则相应的教学策略的要点为：学生识错→转错→省错，教师点错→修错→思错，师生适应→响应→认同；三者既相互对应，又辩证统一．

5结语

本文给出了船的运动为什么是沿绳方向分运动、垂直绳方向分运动的合运动的理论论证，呈现了解决绳-船模型的3种中学物理方法和2种大学物理方法，提供了“同题异法”的一个典型实例；讨论了解决绳-船模型的疑惑，进而奠定了教学的物理理论基础；提出了基于物理过程、物理概念、物理方法解决绳-船模型的参考性教学建议．

或许“不识庐山真面目，只缘身在此山中”，对中学物理疑惑性、难点性问题，其解决的有效途径之一应是回归物理过程、物理概念、规律、物理方法(包括大学物理层次的居高认识)，同时应借鉴相关的教育理论研究成果、教学实践经验，使问题的解决既有坚实的物理依据，又有可靠的教育理论基础和教学实践基础，进而有效培养学生解决物理问题的能力．

参 考 文 献

1方银良．为何绳端速度如此分解．物理教师，2010，31(2)：14

2马皓．再论“为何绳端速度如此分解”．物理通报，2012(1)：109～110

3宋金洪．对一道物理试题的追问．物理教师，2013，34(7)：64～65

4刘桂枝． 顺学而导 补全原解——基于学生“最近发展区”的“拉船模型”纠错策略． 物理教师， 2013， 34(12)： 25～26

5胡盘新，孙迺疆．普通物理学(第5版)习题分析与解答．北京：高等教育出版社，2003．9～10

6Kleppner D，Kolenkow R J．力学引论．宁远源，等译．北京：人民教育出版社，1980．33～35，43

Teaching Research on Rope - ship Models

He Shuping

(Research Institute of Physics Education，College of Education，Northwest Normal University，Lanzhou,Gansu730070)

Abstract：The rope-ship model is a typical kinematics problem，its solution of having already been seen exists puzzling．This paper in detail explores the solution of rope-ship model，the results show that: there are 3 kinds of feasible methods of high school physics，2 kinds of basic college physics methods；the doubles of solving rope-ship model are discussed，and corresponding teaching suggestions are put forward．

Key words：rope-ship model；physics process；physics concept；physics method

(收稿日期：2015-10-10)

作者简介：何述平*何述平(1964-)，男，硕士，副教授，主要从事物理教学论的理论和实验的教学与研究工作．
(西北师范大学教育学院物理教育研究所甘肃 兰州730070)