《周易》数理是什么？

王 俊 龙

(高等学校文科学术文摘 杂志社，上海 200234)



《周易》数理是什么？

王 俊 龙

(高等学校文科学术文摘 杂志社，上海 200234)

摘要：对《周易》数理的认识，有以下六个方面的内容值得注意：一是太极的数理内涵；二是从逻辑的角度分析《周易》中的数理性质；三是布尔代数中存在的概念(或记号)错误；四是无限与“无”的本质联系；五是通过太极代数而证明的哲理与数理的统一性；六是《周易》数理中蕴含的新知识。

关键词：《周易》；太极代数；布尔代数；逻辑；数理；“无”

一、缘起：个人经历的《周易》数理研究

笔者的《周易》数理研究自1990年至今已持续20余年*笔者原为拙著《〈周易〉经传数理研究》(人民出版社2015年)写了导言和结语，但因受篇幅和论域的双重限制，这两部分最终都未能随书稿一起出版。结语的部分内容后来以《太极数理哲学：身心统一的世界观》为题刊于《学术月刊》2013年第6期；本文则是导言的主要内容，发表时新添加了一些必要的注释。需要说明的是，本文中“本文”有时也可代指拙著《〈周易〉经传数理研究》。文中关于《周易》数理的内容、哲学的根本问题等方面听取了审稿专家的意见并添加了注释加以说明，在此表示由衷的感谢！。一开始接触的是演卦中的数理研究，这一研究有整十年时间，是第一阶段。第二阶段是《卦序》中的数理研究，共发表4篇专题论文，这一阶段前后花费约五六年时间。第三阶段是读博3年所做的《周易》文本中的数理研究，完成了博士学位论文《〈周易〉中的数理研究》。第四阶段笔者自己称之为“博士后”的《周易》数理研究阶段。

笔者的《周易》数理研究有两次重要的或决定性的转折：一次是笔者于2006年起师从陈卫平先生攻读中国哲学史博士研究生课程，并于2009年通过博士学位论文答辩。《周易》是一部富含数理的哲学经典，其数理与哲理是紧密联系在一起的。在陈老师的指导下，笔者在思考数学问题的同时也思考专业性的哲学问题，这就使笔者的数学观带有很强的哲学意味，或者说，笔者的哲学观受到数学的深刻影响。一次是笔者于2000年发现“太极代数”*这里要申明的是，笔者发现的太极代数完全不同于谭晓春先生提出的太极代数，尽管他用太极命名代数结构早于笔者。参见谭晓春：《太极代数》，《周易研究》1992年第1期。，笔者用太极命名的太极代数是一种新的、有别于布尔代数的逻辑代数，可称之为非布尔代数(non-Boolean algebra)[1]142。笔者的太极代数是太极阴阳思想与数学高度结合的产物，直到2009年才写入博士论文并公开发表[2]。

博士毕业那年笔者正好满50岁。笔者读博的目的原是想给自己的《周易》数理研究画上一个句号。不过现在看来，那个句号其实只是一个逗号，笔者的新一阶段的《周易》数理研究才刚刚开始。笔者自己设定的“博士后”研究目标的重心是数理逻辑研究，笔者用的工具是太极代数。具体目标有两个：一是用太极代数研究易卦中的逻辑内涵，这是由《周易》数理研究转向《周易》数理逻辑研究；二是将太极阴阳思想引入数学研究，以太极阴阳思想研究逻辑的数学结构。现在看来，笔者的这两个小目标算是实现了，于是才有可能完成《〈周易〉经传数理研究》的写作。

笔者研究《周易》数理的最大感受是，《周易》是一部逻辑形式化乃至形象化的作品。若不明白这一性质，就会导致三个误解：一是依其卦画的象征性，以为《周易》是原始思维的产物，但其中包含朴素的辩证法思想；二是依其卦画的形式化，以为六十四卦是二进制数或布尔向量*二者都是以0和1为元素组成的数学对象。；三是只看到其卦画的形象性及其隐喻的逻辑内涵，以为《周易》中只有类推逻辑而没有形式逻辑。

2011年对笔者的研究来说是比较关键的一年，原因有两个：一是基于空无律和互补律在整个实数系上建立起广义太极代数公理体系*王俊龙：《广义太极代数：R上的逻辑代数》，《湖南师范大学自然科学学报》2014年第5期。其中R含空集，特此说明，下同。。至此，太极代数才真正得以确立，从而有了合乎逻辑的数学解释。同时，布尔代数公理体系中的0-1律和互补律神话也就不攻自破了。二是结合《周易》文本笔者证明了八卦是8个逻辑范式(公式)[3]，进而证明六十四卦是演绎逻辑体系[1]193-218[4-5]。这两项成果可以代表笔者《周易》数理研究中最重要的成果。

在本文中将主要讨论以下几方面内容：一是太极的数理内涵的追问；二是《周易》数理的本质*《周易》卦象数理属于逻辑数理，不能通过算术数理加以解释。因此，本文不涉及《周易》中的“大衍”筮法数理、阴阳爻题数理以及易学中的河洛数理、二进制数理等算术数理。；三是布尔代数中的概念(或记号)错误；四是无限的本质；五是哲理与数理的统一。

二、真相的追问：太极真的是1吗？

《老子》曰：“道生一，一生二，二生三，三生万物。”又曰：“天下万物生于有，有生于无。”

显然，《老子》所言“一”“二”“三”数都是“有”在数量上的反映。在数学上，根据皮亚诺自然数公理系统，1、2、3等诸数生于0[6]。而《老子》所言的“道”无疑与数学上的0相对应，因为0是无。“1、2、3等诸数生于0(无)”与“有(万物)生于无”是不矛盾的。也可以说，《老子》“有生于无”的哲理与自然数的数理是一致的。

邵雍在《皇极经世书》中说：“生而成，成而生，《易》之道也。以天地生万物，则以万物为万物。以道生天地，则天地亦万物也。道为太极。”邵雍所言之“道”即《老子》所言之“道”，并且以太极诠释《老子》所言“道”的内涵。

《系辞上》曰：“是故易有太极，是生两仪。两仪生四象，四象生八卦。”其中的两仪、四象、八卦皆是物象的表现。所有物象生于太极。《乾坤凿度》曰：“天乾，地坤，日离，月坎，风巽，雷震，山艮，泽兑。”郑玄注曰：“八象备，万象生。万象万形，有形之物为象。”

《乾坤凿度》曰：“象成数生。易起无，从无入有。有理若形，形及于变而象。象而后数。”仪、象、卦皆是物象的表现，因此象成而生二、四、八诸数。

显然，从象与数两方面证明，《系辞》所言的“太极”与《老子》所言的“道”在生成万物的功能上是相对应的。道为太极，邵雍的结论是合乎逻辑的。

《乾凿度》曰：“昔者圣人因阴阳，定消息，立乾坤，以统天地也。夫有形生于无形。乾坤安从生？故曰：有太易，有太初，有太始，有太素。”又曰：“太易者，未见气。太初者，气之始。太始者，形之始。太素者，质之始。”郑注曰：“太易之始，漠然无气可见者。太初者，气寒温始生也。太始有兆始萌也。太素者，质始形也。诸所为物，皆成苞裹，元未分也。”《系辞》的作者概括地将有形存在的特征分为阴和阳两方面。《乾凿度》的作者则将有形存在的特征细分为气、形、质三个方面，并且认为这三方面是依此次序先后生成的，从而构想了一个从无中生有的渐进演化过程。其中，质是具体的质料，气是普遍的质料或元素，形是事物的形态。结合邵雍的论证，道为太极，太极为无。

已有的《周易》数理研究说明了这样两个事实：(1)凡是用现有数学理论研究《周易》卦象演绎者，最终都将毫无例外地导致“太极等于1”的结论。(2)凡是用现有逻辑理论研究《周易》卦象逻辑者，最终都会毫无例外地不得不将太极(全域，或全集)设定为1。

造成上述两个事实结果的根本原因：一是所有研究者所掌握的数学工具中都没有摆正太极的真正地位；二是所有研究者所掌握的逻辑工具只有布尔代数，而布尔代数中的全集(或乘法单位元)是1。

如果不把太极放在0的位置上，那么，一个逻辑必然的结果将导致把无极(或太易)放在0的位置上。潘雨廷先生接受了“太极等于1”的事实，于是，他把《老子》所言“复归于无极”中的无极视为0。显然，潘雨廷先生将太极和无极理解为两个概念，并且赋予不同的数学内涵，见图1。

图1数与理的乖违：中西文化的内在冲突*此图根据潘先生的原图绘制(见《潘雨廷先生谈话录》，张文江记述，上海：复旦大学出版社，2012年，第121页)，图的标题是笔者新添加的。

潘雨廷先生将无极理解为0(无)，是将《老子》所言的“无极”与《老子》所言的“道”视为同一个概念。这样的话，问题同时也就出现了。

邵雍论证《老子》所言的“道”是太极。而一旦将太极视为1，太极必将丧失其形而上的质性而沦为形而下的俗物，这也就意味着太极不是《老子》所言的“道”。表面上看这两个矛盾的结论似乎都合乎逻辑，甚至合乎数理。那么问题究竟出在何处呢？

若不接受“太极是1”的事实，太极、两仪、四象、八卦的生成序列中的数理就无法解释。若承认道为太极的说法，实际上意味着接受“太极为无”，而怎样由无生出两仪四象八卦来，现有的(西方的)数学理论不能予以解释。然而，不能用现有数学理论解释，能构成接受“太极为1”的正当理由吗？

其实，在潘雨廷先生的心目中，太极是一个形上的整体概念。他说：“太极就是种种不同的相反的东西合在一起。”[7]281这句话说得没错。问题是：若以为太极为1，把这句话放到布尔代数中去理解在逻辑上也是正确的。太极果真为1吗？

对于0的性质，潘先生说：“无中生有，边界的边界为0。”[7]134那么，“种种不同的相反的东西合在一起”其结果不正是0吗？但是，他前面又明确地说过太极对应1(见图1)。这就证明，在潘先生的思想深处蕴涵着一个深刻的矛盾：数理形式上，他不得不接受太极为1，因为他精通西方数理，比如二项式公式、布尔代数之类。但在思想内涵上，他又把太极看作是一个无所不包的大范围。显然，若要承载太极的这一层意思，“1”这个平凡的数是不够格的。因为他了解并酷爱中国传统文化博大精深的内涵，用一个小小的“1”怎能概括得了？

其实，这个深刻的矛盾不只是存在于潘先生一个人的思想深处，而是早已存在于中国传统文化的思想深处。邵雍曰：“有地然后有二，有二然后有昼夜。二三以变，错综而成。故《易》以二生，数以十二起。而一非数也，非数而数，以之成也。”黄畿注曰：“一无可易，《易》自二生，偶以合奇，始成变化。自三以上，衍于无穷。……一实非数。一乃有二，数由以成。惟一则专，惟二乃化。阳与阴合，参与两倚。倚数可数推，非数则数本也。乃知一体二用不息者，天行之健，有一而已。”[8]

《易纬》的作者说得更明确，矛盾化解得更彻底。《乾坤凿度》曰：“天数一。一者，无也。”“地数二。二者，有偶也。”《易纬》的作者在寥寥数语中竟一气道出了《周易》中的两个根本性原理：一是太极(无)的整体性原理，二是阴阳(二)的对偶性原理。正是在这两个原理的基础上，笔者发现了太极代数。

三、同一性：逻辑中的数理与《周易》中的数理

人们常说：不破不立。笔者则碰到一种立“极”易破“布”难的情形。同时笔者还有一个切身体会是：发现的难度与理解新对象的难度有时往往是相反的。对于广大读者，或许也有如此体会吧。

对于笔者而言，发现太极代数相对容易，因为有前面论述的太极阴阳思想和空无矛盾观作为思想基础。同时又受到《周易》卦象和《太玄》图的直观形象的启发，在爻画数学化(阳爻为1，阴爻为-1，和爻为0)的基础上引进集合运算规则，再经反复推演最终就得到太极代数。更确切地说，笔者是在爻画的数学游戏过程中做出了太极代数。这叫立“极”(太极代数)易。

而发现广义太极代数则要困难得多，困难的原因主要有两方面：一是要克服并超越布尔代数及其公理系统在数学上设置的认知障碍。布尔代数在数学上已经成为一种成熟形态的、公理化的代数结构[9]，要突破它谈何容易。二是布尔代数充其量是建立在实数系中由0到1的闭区间上的[10]，而太极代数与广义太极代数都是建立在整个实数系(需引入Ø与0相对)上的。如何想到并证明在整个实数系可以施行集合运算其难度都相当大。这叫破“布”(布尔代数)难。

发现或想到虽然很难，一旦克服了认知上的障碍，结果反而是广义太极代数要容易理解，这是因为广义太极代数的逻辑变量除了空集就是实数。但要解释清楚太极代数则不是一件十分容易的事。这是因为太极代数完全是一种新的代数结构，又不属于西方ZF公理集合论的范围，于是就不能用西方数学中的现有理论加以解释。这也就意味着太极代数中的数学原理大大超出了笔者(发现广义太极代数前)熟知的数学知识的范围。这也是笔者多年来尝试通过与布尔代数的比较介绍太极代数而始终没有取得任何预期效果的原因。

太极代数的理论基础是广义太极代数，太极代数的逻辑变量并非具体的实数，而是以整个实数系的划分结构为逻辑变量，整个实数系的划分在形式上表现为直观的(甚至可以图像化的)向量结构。《周易》卦象和《太玄》图本质上就是这种向量结构，因而笔者才能受其启发而发现太极代数[1]234-236。

四、逻辑的真相：排除布尔先生设置的雾障

2011年夏，放暑假前笔者从图书馆借了好几本有关公理集合论和数学基础的书，整个假期笔者都在研究西方数学的基础理论。终于，笔者发现太极代数有别于西方数学的根本原因。笔者终于明白，西方数学的根本基础是自然数系统，而数的运算基于算术运算，甚至逻辑运算也借助于算术运算的基本性质。

算术运算的一个鲜明特点是，其负运算对于0是不变的，即-0=0。换言之，0在算术运算中是没有相反对象的，或者说0的逆是其自身。因为西方的公理集合论是建立在算术运算基础上的，而且0没有相异的逆元，因此，ZF公理集合论中认定0=Ø。“空集合Ø一无所有，自然数零也一无所有。因此，把数零定义为空集是合理的。”[11]布尔代数是逻辑代数，其运算规则从根本上说是不同于算术运算规则的。但是，当初布尔在建构思维的代数规则时同时又借用了算术的运算规则。具体表现在：(1)用算术运算中的加法单位元0作为逻辑运算的加法单位元，x+0=x；(2)用算术运算中的乘法单位元1作为逻辑运算的乘法单位元，x·1=x。

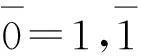
而在太极代数中，0和任何数一样也是有其专门的相反对象的，0是表示无的数学符号，与无相对的是空，表示空的数学符号是Ø。太极代数是完全遵循逻辑运算规则的代数系统。通过太极代数可以发现，在逻辑运算中，1的相反数还是-1，与0相反的数是Ø而不是1。这就避免了逻辑运算与算术运算的混淆。

广义太极代数的建构[12-13]证明：

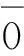
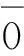
3.在逻辑运算中，的确存在最大元和最小元。但是，最大元不是1，最小元也不是0。Ø才是真正的最小元，没有任何数小于Ø，同时，也没有任何数大于0，0才是真正的最大元。就是说，布尔代数中所谓0，本质上是Ø。布尔代数中的1只是一个普通的数而已，只有对于所有比它小的变量它才是最大的。具体地说，对于Ø到1*注意：不是0到1。区间也分算术区间和逻辑区间两种。在太极代数中，Ø到0的逻辑区间是全集0。因此，Ø到1的逻辑区间(或逻辑变量)是[1]，而1到0的逻辑区间(或逻辑变量)是[-1]。这里的逻辑变量及其符号表示参见王俊龙：《〈周易〉经传数理研究》，北京：人民出版社，2015年，第1页，第232-234页。的逻辑区间中的变量而言，1是其中最大的。

4.在逻辑运算中，乘法单位元是0，加法单位元是Ø。若A是比1小的变量，则依照逻辑运算规则A·1=A，看上去1还真像是算术运算中的乘法单位元。然而，这不过是一种假相罢了。2是比1大的变量，则依照逻辑运算规则有2·1=1(比较：算术运算中2×1=2)，相信现在不再会有人说2也是逻辑乘法单位元。可见，布尔代数中的1并非真正的逻辑乘法单位元，而是逻辑运算中的虚假的乘法单位元。同样的，逻辑加法单位元也不是0，真正的逻辑加法单位元是Ø。布尔代数中的0并非真正的逻辑加法单位元，而是逻辑运算中虚假的加法单位元。

5.布尔代数可以成立，但有一个限制条件，即对于在Ø与1之间的逻辑变量才是成立的。一旦超出这一范围，1不再是逻辑运算中的乘法单位元[13]。也就是说，布尔代数的“0—1律”称不上是真正的公理。这从一个侧面说明，西方数学基于所谓公理的演绎系统难免也蕴藏着巨大的漏洞或认知陷阱。

客观地讲，布尔先生并没有遮蔽世人的双眼，但是，他的确有误导世人的嫌疑。因为他借用算术运算的加法单位元0作为逻辑运算的加法单位元，借用算术运算的乘法单位元1作为逻辑运算的乘法单位元。使其后的绝大多数人(包括专业的逻辑代数学家)都沉湎于他建构的0-1代数系统中。世人满足于它的相对有效性(比如能用于设计开关电路)而不去追问是否绝对完备，甚至，几乎已经认定它是绝对完备的逻辑代数系统。造成这一局面的根本原因是，建立在自然数基础上的算术运算早已深入人心且先入为主，对算术运算过于偏好不仅是中算的显著特征，同样也是西方数学的一个显著特征。

逻辑运算是不同于算术运算的代数运算，通常人们只把逻辑运算看作是集合的演算而不认为逻辑运算也是数的基本性质的表现。因此，逻辑运算在西方数学中并没有获得与算术运算相当的地位，通常把它纳入离散数学的范围。

须申明的是，本文在逻辑乘法的意义上使用布尔乘，同样，在逻辑加法的意义上使用布尔加。本文中的1和0分别是算术运算中的乘法单位元和加法单位元。本文中的0和Ø分别是逻辑运算中的乘法单位元和加法单位元。因为，逻辑运算与算术运算是两种性质完全不同的代数运算。而布尔代数是逻辑代数，所以，布尔代数中的1和0分别是逻辑运算中虚假的乘法单位元和虚假的加法单位元。

为了弄清布尔代数中1和0的庐山真面目，自2000年起，笔者至少花了整整十年时间。可见，要真正弄清楚逻辑运算与算术运算的区别，真正弄清楚逻辑运算中的乘法单位元、加法单位元与算术运算中的乘法单位元、加法单位元的本质区别是何等困难。

五、无限的本质：空和无是一对矛盾

数理是一个整体。数学的结构是数理的外壳，逻辑的结构是数理的内核。二者是紧密联系着的，是一个整体的两面。《周易》数理同样既有其数理的外壳(表现为数学)又有其数理的内核(表现为逻辑)，正因如此，笔者的《周易》数理研究才经历了一个由外(脱离《周易》文本的)到内(结合《周易》文本的)又由内(属于《周易》文本的)到外(超出《周易》文本的)的完整的发展过程。

从事《周易》数理研究需要对数理与哲理两方面(包括相互关系)有最前沿、最深入的理解。有鉴于此，接着想结合对太极阴阳思想的理解略谈一点在研究《周易》数理过程中学习、研究西方ZF公理集合论的个人体会。

《序卦》曰：“丰者，大也。穷大者必失其居，故受之以旅。旅而有所容，故受之以巽。巽者入也。入而后说(脱)之，故受之以兑。”

西方人用一种开放的观点看待宇宙，看待无限，认为无限就是永无尽头。人类能够感知的事物都是有限的，有时，有限的东西与“无”的距离出乎意料的近。“无”是远在天边近在眼前的。西方人看不到身边的“无”，却总是追求远在天边的“无”——遥不可及的无限之境。

但是，无限这个词并非只有没有尽头或没有限度这一层意思；无限的另一层意思是以“无”为限。无限不是无可限，而是以“无”为限，“无”正是无限的尽头。因此，无限并非没有尽头，只不过是无限的尽头不是有而是“无”。西方数学理论以为无限就是没有尽头的观点是一种直观的无限观。任何有(或存在)都不能到达无，因为永远无法到达，感觉就像是永无尽头。无与有(或存在)的关系是，无是一切有(或存在)的总和。

西方数学中并非没有“无”，由空集建构的一切集都是指向无限的。“无”就是无限的尽头，一切集都无以逃脱“无”的范围。数学家(比如康托)建构集合的冲动之所以能够实现，永无止境，是因为有或存在是有限的(所以能够实现)，“无”是无限的(所以不能达到)。

康托用一一对应研究无限集合，比如，他发现在自然数集N和实数集R之间不可能建立一一对应[14]。但其一一对应的方法也不完全是几何上的正比例的方法。一一对应也可以用于互补的两个事物之间的对应关系。比如，男与女是一一对应的，真与假是一一对应的。这种类型的一一对应是整体二分的两部分之间的对应。“无”的本质是不能达到，“无”是近在眼前也不能达到的境域，“无”与大或远并非总是成正比例的关系。“无”是无处不在的，有空的地方就有“无”的所在。

问题是人们常常将空与“无”混为一谈。其实，空与无是孪生的一对。就像阴与阳是一对一样，“无”与“空”是一对，但康托的一一对应中缺少这一对。

所有一切实在都不过是空与无之间的存在，空和无是人类不能进入或达到的境域。西方数学也是空与无之间的建构，尽管ZF公理集合论者只承认“空”或空集而不承认“无”，或在空与无之间画上等号，使“空”失却和“无”之间的一一对应。

只要承认无是一种达不到的境域，就能避免无限的烦恼。只要承认空是什么也没有的空间，就能对拥有的一切倍加珍惜。可以追求无限，但要明白无限以无为限，所有一切尽在无中。欲望的无限膨胀是不能达到的。可以追求空静，但要知道空是无所不在的，空是一无所有的。不能否定一切，也不能舍弃一切。空与无是互补的，相互否定的，相互依赖的。这就是笔者的空无矛盾观。

六、太极代数：哲理与数理的统一

“《周易》有一个理数统一的重要思想，即它的哲学理论与数学知识是有机统一、一一对应的。”[15]构成《周易》数理的基础有两个：一是《周易》文本；二是太极代数。《周易》文本是立论的材料来源，太极代数是论证的逻辑工具。

笔者认为现有哲学探讨的根本问题分为两类*有和无的关系问题或有和空的关系问题是现有哲学讨论中最根本的问题。至于其他哲学问题都可以视为是从这一根本问题上派生的问题。：一类是探讨有与无之间的相互关系，如《老子》提出无中生有的命题；一类是探讨有与空的相互关系，如印度古代哲学(或佛学)[16]。这两个问题都倾向于把“空”或“无”作为“有”的对立面而提出。

上述哲学问题都视有和无，或空和有是一对矛盾关系。哲学中的问题哪怕是最基本的哲学问题都会在数学中有所反映。哲学上的基本问题往往是围绕矛盾关系展开的。矛盾双方构成矛盾集合的元素，而最适合研究矛盾关系的数学工具是集合运算。反映有与无关系的数学是布尔代数。如果空是“绝空”的话，空与有的问题在数学上也可以通过布尔代数加以反映。关于有和无的布尔代数与关于空和有的布尔代数在数学上是对称的关系。这种对称关系容易被理解为知识结构上的对应性，从而在二者之间形成语义上的互释关系。

“大致说来，依真谛世间是‘空’，依俗谛世间是‘有’，所以真、俗二谛也是空、有二谛。大乘的基本立场就是‘俗有’而‘真空’。我们认为这种‘空’、‘有’之分，与海氏的存在论的‘有’、‘无’之辨，基本精神是一致的。”[17]其实，哲学上的根本问题既非有和无的问题也非空和有的问题，而是空和无的关系问题。空和无的问题出现在“有”尚未呈现之前，因而是更根本的问题。空和无是什么关系呢？在此，空和无不是同一个概念的不同表述，二者之间不可画等号。这不但是与常识相反的结论，与西方某些数学理论也是一个相反的结论。

太极代数是建立在“空、无、阴、阳”四元概念基础上。阴与阳互补，空与无互补。“太极无分(亦谓无名，有名则有分)”[18]，有(有名)是分阴分阳的相对存在，空与无是存在的绝对前提。阴阳合则同归于无(无名)，阴阳分则两立于空(空名)。空与无是一对先天的或绝对的矛盾，空与无也是一对可以自足、自洽施行逻辑演算的相反数。

空和无才真正构成一对矛盾关系。空是万有的起始，无是万有的终结。从数理上可以证明，空和无是最朴素的矛盾集合，在其上定义布尔加、布尔乘和补运算构成太极代数[19]。在此阶段，太极代数是用数学的语言反映空与无之间的互补关系或矛盾关系。太极代数是笔者根据《周易》的太极阴阳思想提出来的，太极代数体现哲理与数理的高度统一，见表1(见下表)，但其中的具体内容因篇幅所限，这里就不全面论述了。

在空和无形成的矛盾集合中可以引进“有”，但“有”是包含矛盾的存在。就是说，“有”是分阴分阳的，有的“有”是阴性的，有的“有”是阳性的。有阴性的“有”必有阳性的“有”与之相对，这就叫“孤阴不生，孤阳不长”。世上既没有孤阴也没有独阳，阴和阳是相对存在的。因此，引进“有”就是在空和无的矛盾基础上引进阴与阳的矛盾关系。这样，我们得到一个新的矛盾集合，其中包含四个元素：空、无、阴、阳。这个新的集合中有两对矛盾关系。像前面一样，在其上可以定义布尔加、布尔乘和补运算，结果也是太极代数。在此阶段，太极代数通过数学的语言反映“空、无、阴、阳”四元素之间的关系。

太极代数的建立说明，西方哲学中有和无之间的关系与印度哲学中空与有之间的关系在数学上表现为“空、无、阴、阳”四元素之间的关系。在太极代数中“有”是作为阴阳矛盾的两方面加以反映的。

表1　太极代数：哲理与数理的统一

①布尔代数中的0作为空类(或空集)符号使用。

②印度哲学中的“空”并非一无所有的绝空，有时也有“无”的意思。参见王俊龙：《本体逻辑学新探》，《陕西师范大学学报》(哲学社会科学版)2015年第2期，第5-16页。

因此，笔者认为最基本的哲学问题往往也是一个最基本的数学问题，笔者的哲学观点与太极代数是密切相关的。虽然，笔者的哲学观点来自《周易》，但是，笔者把太极阴阳思想引入了数学研究之中，这才有了太极代数。

七、结语：几点补充说明

围绕《周易》数理，笔者要做以下几方面的总结或说明。

第一，其内容涵盖哲学、逻辑学、代数学三门学科，但其主要内容还是围绕《周易》中的数理(或符号逻辑)。

第二，从知识形态讲，其中的部分内容属于哲学、逻辑学、代数学三门学科的交叉部分，这部分内容不完全属于哲学、逻辑学和数学中任何一门学科。这也就印证了笔者有时会产生没有明确的学科归属感的体会。

第三，虽然从概念上看，其中的部分内容属于哲学、逻辑学、代数学三门学科的交叉部分或三者的结合，但并非意味着是现有的哲学、现有的逻辑学、现有的数学的交叉内容，而是整个哲学(包括现在还没有的部分)、整个逻辑学(包括现在还没有的部分)、整个数学(包括现在还没有的部分)的交叉部分。换言之，这部分内容不是现有哲学、逻辑学、代数学三门学科知识的简单拼凑或综合，其中包含一些新的元素、新的方法和新的思想。这“三新”说明其内容的创新性。

第四，因为上述第三点，虽然其内容脱胎于《周易》数理，但有些内容并不局限于《周易》数理。同样，其中的哲理虽然是以易理为基础的，但其内容并不局限于易理；其中的代数内容虽然取材于西方数学，但其内容并不局限于西方数学。这三个“不局限于”说明其内容的超越性。

第五，其中的部分内容是哲学、逻辑学、代数学三门学科的交叉部分或三者的结合，还涉及哲学和逻辑学相结合形成的哲理逻辑，如黑格尔的《逻辑学》、维特根斯坦的《逻辑哲学论》；还涉及逻辑学和代数学相结合形成的逻辑代数，如布尔代数、集合代数；还涉及哲学和代数学相结合形成的哲理代数，如笔者提出的太极代数，是太极阴阳思想与数学相结合的产物；还涉及数理哲学，如罗素的《数理哲学导论》。这些两两结合说明其内容的丰富性。

第六，其内容之所以有创新性、超越性和丰富性主要是源于《周易》太极阴阳思想的高度概括性、绝对超前性和无比深刻性。因此，太极阴阳思想是打开《周易》数理的锁钥，太极阴阳思想是本文内容的主线。

上面所谈的是笔者研究《周易》数理的大致过程和笔者所理解的数理观。其中有一个实实在在的展开基础的探索过程(有时充满艰辛)，其间贯穿一个超凡脱俗的空无矛盾观(有时难免误解)，这是本文得以完成的两个不可或缺的条件。

《说卦》曰：“八卦相错，数往者顺，知来者逆，是故易逆数也。”根据笔者二十多年来研究《周易》数理的感受与体会偶得下面四句话，愿与读者同道分享：

逆数自空无，万物分阴阳。卦象是逻辑，易道非寻常。

参考文献：

[1]王俊龙.《周易》经传数理研究[M].北京：人民出版社，2015.

[2]王俊龙.论太极代数及其辩证内涵[J].湖南师范大学社会科学学报，2009(3)：43-47.

[3]王俊龙.论八卦是八个逻辑范式[J].周易研究，2012(3)：90-96.

[4]王俊龙.论六十四卦是演绎逻辑系统(上)[J].东亚文献研究，2013(12)：133-142.

[5]王俊龙.论六十四卦是演绎逻辑系统(下)[J].东亚文献研究，2014(13)：17-26.

[6]罗素.数理哲学导论[M].晏成书，译.北京：商务印书馆，1999：11.

[7]张文江.潘雨廷先生谈话录[M].上海：复旦大学出版社，2012.

[8]邵雍.皇极经世书[M].黄畿，注.郑州：中州古籍出版社，1993：335-336.

[9]杨炳儒.布尔代数及其泛化结构[M].北京：科学出版社，2008：9-45.

[10]亚格洛姆.不平常的代数[M].方伟武，译.北京：知识出版社，1984：26-28.

[11]张锦文.公理集合论导引[M].北京：科学出版社，1991：28.

[12]王俊龙.太极数理哲学：身心统一的世界观[J].学术月刊，2013(6)：27-35.

[13]王俊龙.广义太极代数：R上的逻辑代数[J].湖南师范大学自然科学学报，2014(5)：85-89.

[14]周·道本.康托的无穷的数学和哲学[M].郑毓信，刘晓力，编译.大连：大连理工大学出版社，2008：34-41.

[15]周瀚光.先秦数学与诸子哲学[M].上海：上海古籍出版社，1994：10.

[16]释印顺.性空学探源[M].北京：中华书局，2011：1-10.

[17]吴学国.存在·自我·神性：印度哲学与宗教思想研究[M].北京：中国社会科学出版社，2006：135-136.

[18]汤用彤.魏晋玄学论稿[M].增订本.北京：生活·读书·新知三联书店，2009：67.

[19]王俊龙.棋法阴阳：围棋中的哲理与数理[J].西南大学学报(社会科学版)，2013(6)：11-19.

责任编辑韩云波

网址：http://xbbjb.swu.edu.cn

中图分类号：B221

文献标识码：A

文章编号：1673-9841(2016)02-0021-09

基金项目：上海师范大学科研基金项目“本体逻辑学研究”(A-0230-14-001107)，项目负责人：王俊龙。

作者简介：王俊龙，哲学博士，高等学校文科学术文摘杂志社，副研究员。

收稿日期：2015-07-29

DOI：10.13718/j.cnki.xdsk.2016.02.003