空间目标初始轨道确定吉布斯问题误差分析

刘庆博，任顺清

（哈尔滨工业大学 空间控制与惯性技术研究中心，哈尔滨 150080）

空间目标初始轨道确定吉布斯问题误差分析

刘庆博，任顺清

（哈尔滨工业大学 空间控制与惯性技术研究中心，哈尔滨 150080）

现代战争中的空间武器平台捕获敌方的空间目标，确定其运行轨道后实施军事打击，所以对轨道确定参数的误差进行分析对于精确打击具有非常重要的意义。为了准确分析吉布斯三位置矢量定轨法的轨道根数的确定精度，根据吉布斯方法的轨道确定模型，采用向量求导的方法，详细推导了轨道根数对于观测位置误差的灵敏度矩阵，并给出了轨道根数误差与观测位置误差之间的关系，明确初始轨道的确定精度及误差传播规律。最后对吉布斯方法及其误差分析进行仿真分析验证，验证了方法的正确性。

初始轨道确定；吉布斯方法；轨道根数；灵敏度矩阵

在轨道力学中，对空间目标进行轨道确定包括两个过程：利用短弧段观测数据的初始轨道确定以及长弧段下的精密定轨[1]。初始轨道确定一般都是采用二体模型，经典的初始轨道确定方法都是利用测角数据来进行计算的，主要有Laplace法和Gauss法两种。

长期以来，国内外的众多学者都针对以上两种方法进行了更加深入的研究，并提出了多种初始轨道确定的方法，解决了一些使用传统方法会出现不收敛或不稳定等问题。文献[2]基于单站单圈测量数据研究了低轨卫星初轨确定的方法，对遗传算法和最小二乘法在不同观测条件下确定的初轨信息以及轨道预测信息进行了分析和比较，确定了两种方法的优缺点和各自的适用条件。文献[3]采用最小一乘方法建立了一种初轨计算的稳健方法，将初轨计算问题转换为线性规划问题求解，并通过bootstrap方法给出估计精度，数值计算结果表明该方法稳健有效，并具有较高的崩溃点。文献[4]将采用角度和角速率数据进行初始轨道确定与只采用角度数据进行了对比，采用角度和角速率数据有着更好的平稳性和可靠性。文献[5]提出了一种采用单时刻 GPS测量的方法来对地球静止卫星进行初始轨道的确定，并采用EKF对该算法进行了验证。文献[6]利用遗传算法来对极短弧的光学观测进行初始轨道确定，并利用蒙特卡洛仿真来验证算法的可靠性。文献[7]将天基角度测量与遗传算法相结合来确定初始轨道，得到了满意的结果，并且多种群遗传算法（MPGA）可以有效解决角度测量方法的迭代过程中出现的问题。文献[8]中根据开普勒运动定律推导出确定斜距的方法，5个数据一组进行初始轨道的确定。除此之外，还可以利用其他方法来确定初始轨道，如利用高斯混合模型求解[9]。以上是对初始轨道确定方法研究现状的概述，对轨道确定方法进行误差分析的相关文献相对较少。文献[10]中分析了星载GPS接收机的定位误差对卫星轨道根数的影响，只推导了长半轴，轨道倾角和升交点赤经的误差与位置、速度误差的关系式。

本文将主要对吉布斯三位置矢量定轨法进行误差分析。首先给出轨道根数的计算方法和吉布斯三位置矢量定轨法。利用3个位置矢量就能确定轨道根数，但目前没有文献给出位置矢量本身的测量误差、夹角的大小等对于6个轨道根数确定误差的影响程度。在整个轨道确定的过程中，初始轨道确定的精度大多数情况下无法满足精度要求，需要进行精密定轨，而初始轨道确定的精度往往会影响精密定轨初值的选取，高精度的初始轨道的确定可以减少整个轨道确定的时间。所以本文将对吉布斯方法进行误差分析，推导出6个轨道根数的灵敏度矩阵，明确误差传播特性，并对其进行仿真分析与验证。

1 轨道根数与初始轨道确定

1.1 轨道根数

轨道根数是用来描述天体在其轨道运行状态的一组参数。6个轨道根数如图1所示，其中，h为比角动量的模，i为轨道倾角，Ω为升交点赤经(RA)，e为偏心率，ω为近地点幅角，θ为真近点角，a为长半轴。当已知位置矢量和速度矢量

求解上述轨道根数的过程如下：

径向速度大小vr为

根据文献[11]，直接给出6个轨道根数的算法，比角动量h：

图1 轨道根数Fig.1 Orbital parameters

轨道倾角i：

升交点赤经Ω：

偏心率矢量e为地心O指向近地点的矢量，表达式为

偏心率e为偏心率矢量e的模。

近地点幅角ω：

真近点角θ：

长半轴a：式中：μ = GMe是地心引力常数，μ = 398600km3/s2，Me是地球质量。

下面针对a、i、Ω、e、ω、θ这6个轨道根数进行误差分析。

1.2 初始轨道确定——吉布斯三位置矢量定轨法

如果测量出空间目标轨道上P1、P2、P3位置的位置矢量 r1、r2和r3后，便可用吉布斯三位置矢量定轨法来计算6个轨道根数。如图2所示。

其中，

根据式(9)，角动量h可由r1、r2和r3通过如下关系得到：

图2 吉布斯三位置矢量定轨Fig.2 Gibbs’ method for initial orbit determination

从式(13)可以看出，测量得到3个位置矢量，能计算过度矢量N、D、S及其相应的标量，再计算速度矢量，最后根据式(1)～(8)确定6个轨道根数。然而测量的矢量r1、r2和r3是有误差的，而且它们之间的夹角有大有小，如何根据位置矢量的误差来确定6个轨道根数的误差就是下面将要研究的内容。

2 初始轨道确定方法的误差分析

对吉布斯三位置矢量定轨法进行误差分析，要根据6个轨道根数的计算公式写成关于3个位置矢量r1、r2和的微分表达式，求取关于 r1、r2和r3的偏导，转换成矩阵的形式，得到6个轨道根数a、i、Ω、e、ω、θ的灵敏度矩阵，并且h作为重要的中间变量同样需要求取灵敏度矩阵。在求解过程中，主要利用向量对向量求偏导的相关计算公式以及如下几个常用的求取偏导公式：

1）如果M为矢量M的模，m为另一矢量，则：

首先求取比角动量的模 h对位置矢量的灵敏度矩阵。根据轨道比角动量为常矢量，h=r×v，将第2个位置的速度v2的表达式代入可以得到

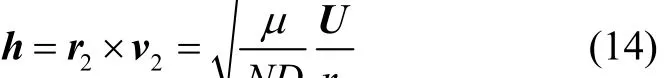
NDr

2

将比角动量h对r1、r2和r3求导，则h的误差与位置误差δ1r、δr2和δr3的关系为

对位置矢量求导，得：

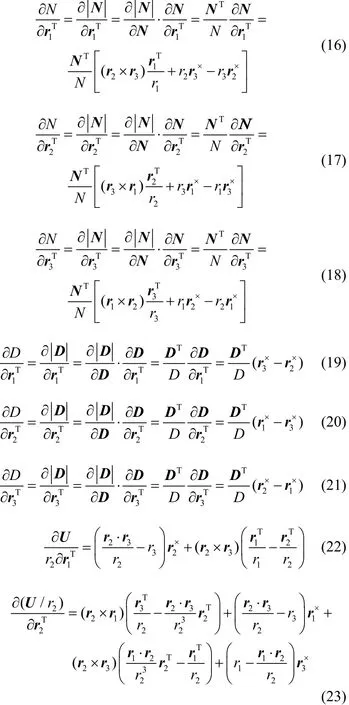
根据式(15)，写出矩阵：

式中，比角动量的灵敏度矩阵

为3×9维的矩阵，其中各个元素的计算可将公式(16)～(24)代入即可计算，它们均是矢量 r1、r2和r3及其标量的函数。计算比角动量的模的灵敏度矩阵为其他5个轨道根数的灵敏度矩阵求取方法

类似，略去详细推导。

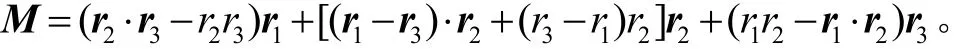
速度的灵敏度矩阵Av为

其中，

长半轴a的灵敏度矩阵为

轨道倾角i的灵敏度矩阵为

升交点赤经Ω的灵敏度矩阵为

偏心率e的灵敏度矩阵由偏心率矢量e的灵敏度矩阵得到，则：

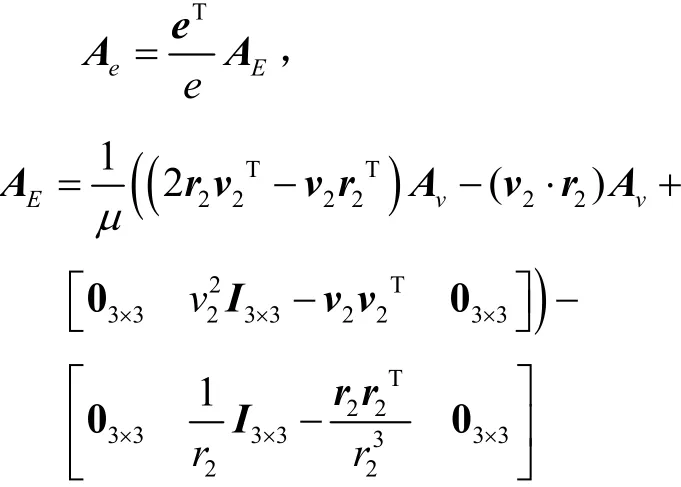
真近点角θ的灵敏度矩阵Aθ为

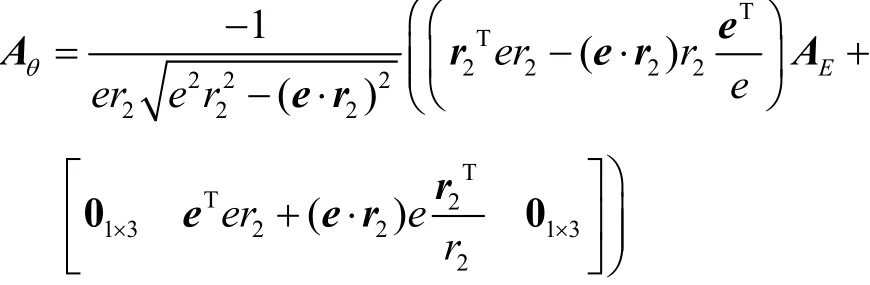
求取近地点幅角的灵敏度矩阵前先求解出矢量B关于位置误差的灵敏度矩阵ΑB为

继而求解出近地点幅角的灵敏度矩阵Αω为

标量对位置矢量的灵敏度矩阵均为1×9维矩阵，假设各个位置矢量测量的不确定度相等，均为σ，并假设各次测量均为独立测量，再结合不确定度的合成公式，即当所求取轨道根数的灵敏度矩阵为A时，那么轨道根数的不确定度为表示灵敏度矩阵的元素，就可求出6个轨道根数的不确定度。

3 初始轨道确定方法的仿真分析

利用STK软件绘制轨道，设定轨道参数如下：

在绘制好的轨道上选取3个位置矢量（km）：

对吉布斯三位置矢量定轨法进行Matlab编程，经过计算可以得到6个轨道根数，长半轴轨道倾角偏心率 e= 0.100132，升交点赤经近地点幅角真近点角

把以上建立的运行轨道模型中的位置信息当作基准数据，在基准数据中加入0.1 km的位置随机误差，多次取值，求取6个轨道根数的不确定度，并在此基础之上逐步增大选取的 3个位置矢量之间的夹角，最大到120°左右，观察6个轨道根数不确定度的变化趋势，绘（相对于位置矢量r）。制出变化曲线。令位置不确定度根据前面得到的6个轨道根数的灵敏度矩阵，计算6个轨道根数的不确定度，与由仿真数据计算得到的不确定度进行比较，仿真结果如图3～8所示。

图3 长半轴a与位置误差的关系Fig.3 Relationship between semimajor axis and position error

图4 轨道倾角i与位置误差的关系Fig.4 Relationship between inclination and position error

图5 升交点赤经Ω与位置误差的关系Fig.5 Relationship between right ascension of the ascending node and position error

图6 偏心率e与位置误差的关系Fig.6 Relationship between eccentricity and position error

从上述仿真结果可以看到，利用吉布斯三位置矢量定轨法计算得到的轨道根数与预设的轨道根数接近，由实际数据计算得到的轨道根数的不确定度与由灵敏度矩阵计算得到的轨道根数的不确定度，两者的结果十分接近，验证了前面所求取的轨道根数的灵敏度矩阵的准确性。从轨道根数的不确定度的变化趋势可以看到，增大选取位置矢量之间的夹角，6个轨道根数的不确定度在减小，所以尽量增大选取的3个位置矢量之间的夹角有利于减小轨道根数的误差。但实际确定初始轨道时，增大3个位置的夹角可能受到所需确定时间的限制，可根据具体所需的轨道确定精度和效率进行取舍。

图7 真近点角θ与位置误差的关系Fig.7 Relationship between true anomaly and position error

图8 近地点幅角ω与位置误差的关系Fig.8 Relationship between argument of perigee and position error

4 结 论

针对吉布斯方法确定的6个轨道根数的误差，推导了6个轨道根数误差相对于位置矢量测量误差的灵敏度矩阵，用Matlab软件编程计算了6个轨道根数的不确定度；然后，利用STK软件绘制轨道，验证了空间目标初始轨道确定方法的有效性；最后，对选取位置矢量之间的夹角做出改变进行了仿真分析，绘制了轨道根数不确定度的变化曲线，将真实数据计算得到的不确定度与由灵敏度矩阵计算得到的不确定度进行比较，验证了前面所求取的灵敏度矩阵的准确性。由仿真结果可知，为减小轨道根数的误差，可以通过增大选取的3个位置矢量之间的夹角来实现。在实际的初始轨道确定中，可根据本文给出的6个轨道根数灵敏度矩阵可以计算出所求解的轨道的轨道根数误差。

（References）：

[1] 刘林, 王海红, 胡松杰. 卫星定轨综述[J]. 飞行器测控学报, 2005, 24(2): 28-34. Liu Lin, Wang Hai-hong, Hu Song-jie. Summary on satellite orbit determination[J]. Journal of Spacecraft TT&C Technology, 2005, 24(2): 28-34.

[2] 李振华, 鲜勇, 刘炳琪, 等. 单站单圈卫星初轨确定方法研究[J]. 火力与指挥控制, 2014, 39(12): 123-126. Li Zhen-hua, Xian Yong, Liu Bing-qi, et al. Study on initial orbit determination with single lap radar station[J]. Fire Control & Command Control, 2014, 39(12): 123-126.

[3] 王歆. 一种初轨计算的稳健方法[J]. 天文学报, 2013, 54(3): 274-281. Wang Xin. A robust method of preliminary orbit determination[J]. Acta Astronomica Sinica, 2013, 54(3): 274-281.

[4] Demars K J, Jah M K, Schumacher P W. Initial Orbit Determination using Short-Arc Angle and Angle Rate Data[J]. IEEE Transactions on Aerospace & Electronic Systems, 2012, 48(3): 2628-2637.

[5] Ghangho K, Chongwon K, Changdon K. Coarse initial orbit determination for a geostationary satellite using single-epoch GPS measurements[J]. Sensors, 2015, 15(4): 7878-7897.

[6] Ansalone L, Curti F. A genetic algorithm for initial orbit determination from a too short arc optical observation[J]. Advances in Space Research, 2013, 52: 477-489.

[7] Liu L, Tang G, Hu S. Initial orbit determination based on sparse space-based angle measurement and genetic algorithm[C]//2013 IEEE International Conference on Information and Automation. 2013: 850-855.

[8] Vitarius P J, Hahs D, Gregory D A. A Keplerian approach to angles-only orbit determination[C]//Defense and Security Symposium. International Society for Optics and Photonics, 2006: 62200M/1-62200M/7.

[9] Demars K J, Jah M K. Probabilistic initial orbit determination using Gaussian mixture models[J]. Journal of Guidance Control & Dynamics, 2013, 36(5): 1324-1335.

[10] 初东, 王刚. 星载 GPS接收机定位误差对卫星轨道根数的影响分析[J]. 测绘科学, 2014, 39(6): 31-34. Chu Dong, Wang Gang. Influence of spaceborne GPS receiver positioning errors on satellite’s orbital elements[J]. Science of Surveying and Mapping, 2014, 39(6): 31-34.

[11] Curtis H D. Orbital mechanics for engineering students [M]. Burlington: Butterworth-Heinemann, 2010.

[12] 夏红伟, 李秋实, 李莉, 等. 基于hp自适应伪谱法的飞行器再入轨迹优化与制导[J]. 中国惯性技术学报, 2015, 23(6): 818-823. Xia Hong-wei1, Li Qiu-shi, Li Li, et al. Trajectory optimization and guidance for reentry craft based on hp-adaptive pseudospectral method[J]. Journal of Chinese Inertial Technology, 2015, 23(6): 818-823.

Error analysis of Gibbs’ method for initial orbit determination of space target

LIU Qing-bo, REN Shun-qing

(Space Control and Inertial Technology Research Center, Harbin Institute of Technology, Harbin 150080, China)

In modern war, the space weapon platform can capture enemy’s space target and then attack it after determining the orbit, so the error analysis of orbital parameters is of great significance. To precisely analyze the orbit-determination accuracy of orbital elements by Gibbs three-position vector method, the sensitivity matrices of orbit parameters versus the position errors are deduced by using the vector derivatives according to the model of Gibbs’ method. The precision of initial orbit determination and error propagation characteristics are determined by the relationship between the orbital parameter errors and position errors. Simulation results show the correctness of the Gibbs method and its error analysis.

initial orbit determination; Gibbs’ method; orbital parameter; sensitivity matrix

U666.1

A

1005-6734(2016)02-0263-06

10.13695/j.cnki.12-1222/o3.2016.02.023

2015-12-14；

2016-03-11

装备预研基金项目（9140A09030313HT01121）；国家重大科学仪器设备开发专项（2013YQ310737）

刘庆博（1991—），男，博士研究生，从事惯性技术研究。E-mail: lqb9104@163.com

联 系 人：任顺清（1967—），男，教授，博士生导师。E-mail: renshunqing@hit.edu.cn