基于鲁棒滤波的捷联导引头视线角速度估计方法

王小刚，胡智勇，于 洋，秦武韬

（1. 哈尔滨工业大学 航天学院，哈尔滨 150001；2. 空军大连通信士官学校，大连 116600；3. 国营第六二四厂，哈尔滨 150030）

基于鲁棒滤波的捷联导引头视线角速度估计方法

王小刚1，胡智勇2，于 洋3，秦武韬1

（1. 哈尔滨工业大学 航天学院，哈尔滨 150001；2. 空军大连通信士官学校，大连 116600；3. 国营第六二四厂，哈尔滨 150030）

针对捷联导引头无法直接获取视线角速度等信息的问题，研究了鲁棒滤波在大气层外飞行器捷联导引头视线角速度估计中的应用。为了建立非线性滤波估计模型，考虑目标视线角速度的慢变特性，采用一阶马尔科夫模型建立了状态方程；推导了视线角速度的解耦模型，并建立了量测方程；考虑到实际应用中存在系统噪声统计特性失准的问题，基于Huber-Based鲁棒滤波方法，设计了视线角速度滤波器，并完成了基于 Huber-Based滤波方法和扩展卡尔曼滤波方法的数学仿真。仿真结果表明Huber-Based滤波方法的视线角、视线角速度及视线角加速度估计精度分别达到 0.1140′、0.1423′/s、0.0203′/s2，而扩展卡尔曼滤波方法的视线角、视线角速度及视线角加速度估计精度仅分别为0.6577′、0.6415′/s、0.0979′/s2。仿真结果证明了该方法可以有效地估计出相对视线角速度等信息，并且在非高斯噪声的条件下，依然可获得较高的估计精度，具有一定的鲁棒性。

捷联导引头；视线角速度；一阶马尔科夫模型；非线性滤波方法；Huber-based滤波

为了应对弹道导弹的威胁，美俄等军事强国先后开展了导弹防御系统[1]（Missile Defense System, MDS）的相关技术研究。特别是美国已经建立了一套多基、分层导弹防御系统，其核心组成部分之一就是大气层外拦截器[2]，而高精度末制导律设计是保证其拦截精度的关键技术[3]。传统的大气层外拦截器末制导依赖于红外导引头，制导律采用比例导引法。然而，随着捷联导引头的出现，成本低、重量轻等一系列优势使其逐渐成为军事领域的研究热点[4]。然而捷联导引头只能测量目标的相对视线角，无法直接获得视线角速率，导致比例导引等传统制导律无法应用。因而，捷联导引头的末制导律设计问题逐渐成为当前的一个研究热点问题。

为解决上述问题，研究人员提出了两种技术途径：一种是设计与捷联导引头测量特性相适应，只利用视线角信息进行制导的捷联制导算法。文献[5]以经典制导律为基础，提出了多种捷联律设计方案，并采用姿态角反馈自动驾驶仪和过载反馈自动驾驶仪构造了捷联制导系统，并进行了仿真验证。然而，该研究以反辐射导弹为应用背景，对于大气层外飞行器的高速、大过载情况，其适应性尚未得到验证。另外一种技术途径是基于捷联导引头的测角信息，提取目标视线角速率，进而采用比例导引法完成制导任务。由于捷联导引头的测角信息中包含噪声，采用直接微分的方法会放大噪声，淹没角速率信息[6]，因而目前常用的方法是非线性滤波估计法。文献[7]提出了一种基于粒子滤波的捷联导引头视线角速率估计方法。文献[8]设计了一种H∞平方根滤波器，估计出弹目相对运动等信息，可有效对付机动目标。文献[9]针对某型制导弹药末制导问题，采用强跟踪卡尔曼滤波方法提取相对运动信息，用于最优导引律实现。综上，在采用非线性滤波方法估计视线角速率信息时，其关键问题包含如下三个方面：一是非线性滤波算法的选取，要兼顾考虑估计精度和计算量两个因素；二是视线角速度率信息重构，即建立视线角与实现角速度率之间的关系，该问题的研究目前已相对成熟；三是状态方程的建立，需要结合具体问题进行设计。文献[7-9]的状态方程基于弹目相对运动关系，假设目标运动加速度符合某种统计规律，如一阶马尔科夫模型。因而，该方法仅适用于机动性较差的地面慢速目标。本文将利用一阶马尔科夫模型建立系统的状态方程，结合 Huber-Based滤波算法以及视线角速度解耦模型实现对目标视线角等信息的有效估计

1 Huber-Based滤波算法

鲁棒性是指当参数与假设分布存在偏差时，系统对偏差不敏感的特性。在实际应用中，由于内外部不确定因素的影响会造成系统噪声的先验统计特性不准确或噪声特性不稳定，进而影响整个系统的精度。为解决这个问题，Huber提出了广义极大似然估计[10]，即 M 估计。本文将滤波系统的量测更新转化为用Huber估计的方法[11]，具体如下：

假设有如下离散系统：

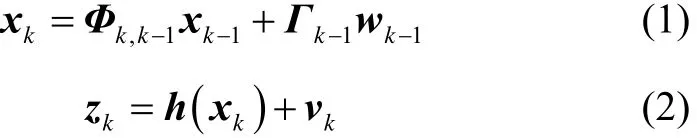
式(1)为系统的状态方程，式(2)为系统的量测方程，其中，为第k-1时刻到第k时刻的一步转移矩阵，Γk-1为系统噪声驱动矩阵，xk和zk分别为系统的状态值和量测值，wk为系统激励噪声序列，vk为量测噪声序列。

1.1 状态预测

将第k时刻系统状态的估计值记为xˆk，状态估计误差协方差阵记为Pk，根据系统方程，第k时刻预测的状态估计值和协方差为

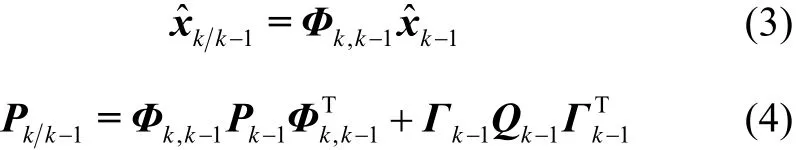
1.2 量测更新

对于给定的量测值zk-1，滤波更新是所构造的线性回归问题的解，因此，将滤波更新问题转换为线性回归问题，有：

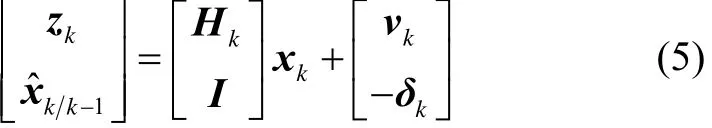
定义如下变量：

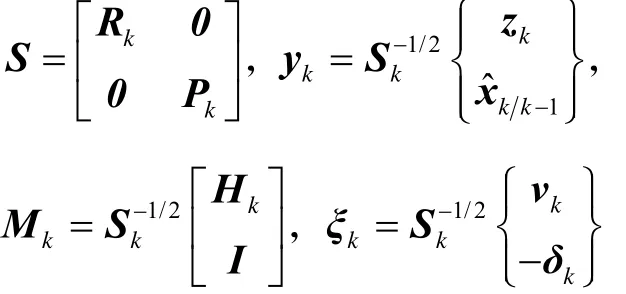
Huber-Based滤波的量测更新值可以通过求解如下指标函数获得：

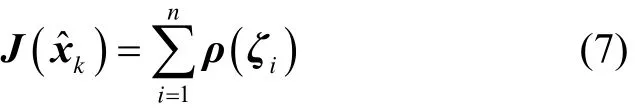
式中，ζi为ζ的第i个元素，且为损失函数（或目标函数）。

尽管ρ函数在一定程度上可以选择，但为保证式(7)有解，ρ函数须满足以下三个条件：

1）ρ在R中处处连续；

3）矩阵M满秩。

Huber给出了如下ρ函数形式：

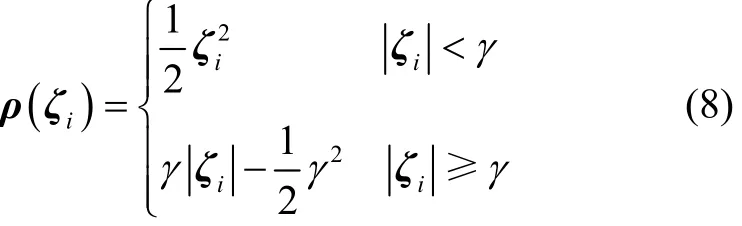
式中，γ为调节参数。

式(8)中ρ函数是l1范数最小和l2范数最小的混合方程。调节参数γ→0，式(8)为l1范数最小；调节参数γ→∞，式(8)为l2范数最小。Huber已证明，当ρ函数选择式(8)的形式，Huber-Based滤波对受污染的高斯分布具有渐进最优鲁棒性[12]。

而最小化指标函数(7)的解满足如下方程：

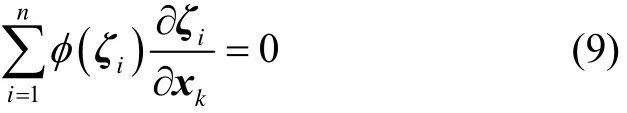
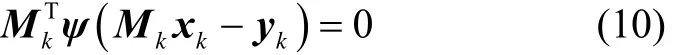
通过迭代可求出式(10)的解：

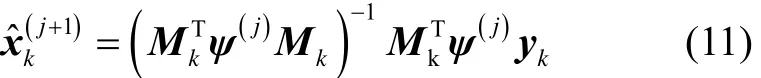
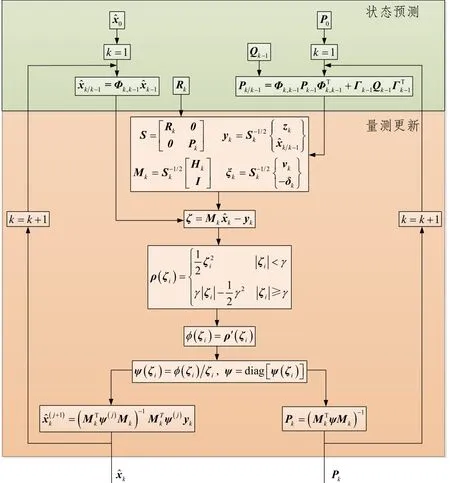
图 1 Huber-Based滤波流程图Fig.1 Flow chart of Huber-based filter

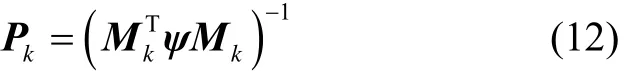
Huber-Based滤波的流程图如图1所示。

2 捷联成像导引头视线角速率估计

2.1 坐标系及其转换

为研究捷联成像导引头视线角速率估计算法，引入发射惯性坐标系、弹体坐标系、视线坐标系和体视线坐标系。各坐标系定义如下：

其转换关系如图2所示。图2中：

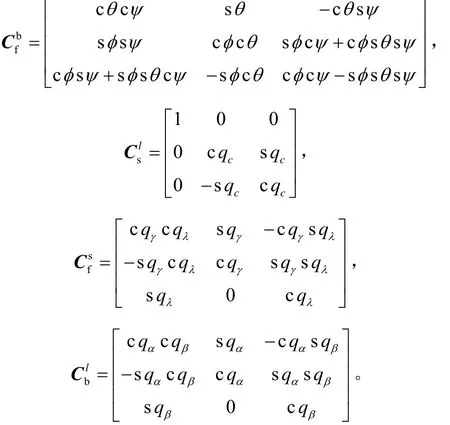
上述诸式中，θ、ψ、γ分别为俯仰、滚转、偏航角，qα为体视线高低角，qβ为体视线方位角，qγ为视线高低角，qλ为视线方位角，qc为视线变换角，s、c分别表示sin和cos。

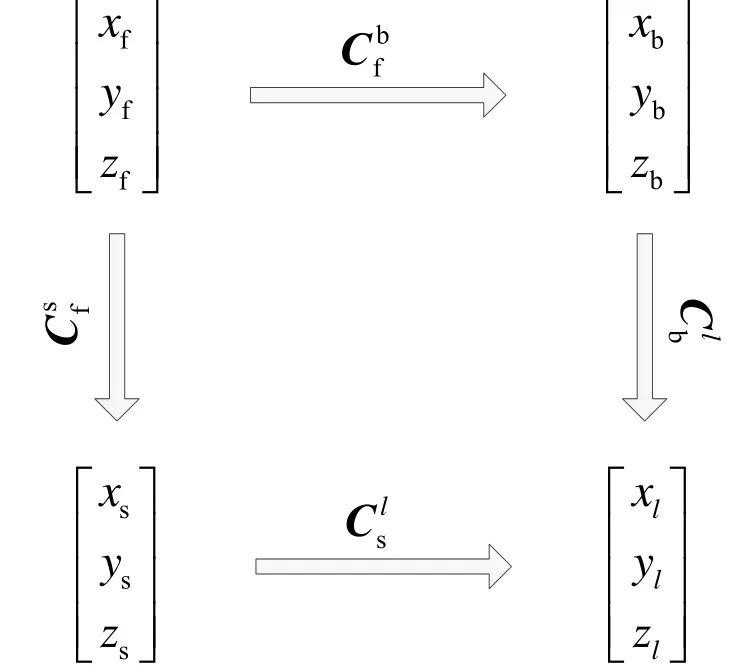
图2 坐标系间转换关系Fig.2 Transformation relationship between coordinate systems

2.2 系统状态模型

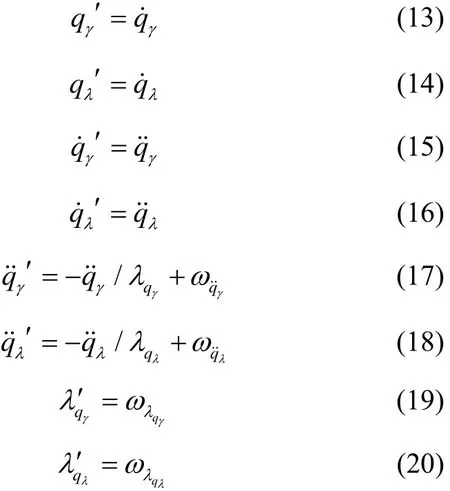
状态方程的连续形式为

其离散形式为

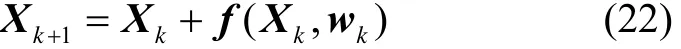
式(21)(22)中， f为式(13)～(20)的联立形式。

2.3 系统量测模型

考虑到捷联成像导引头可直接测量体视线高低角qα及qβ，故将其作为量测量，但仍需建立状态量与其之间的联系，而目标在视线坐标系和体视线坐标系中的坐标均为则目标在体坐标系和发射惯性坐标系中的坐标分别为

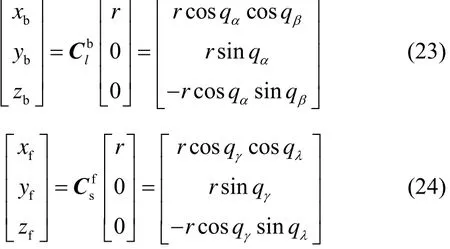
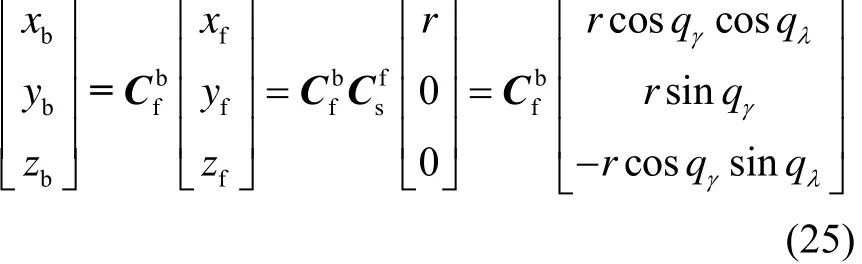
联立式(23)，有：

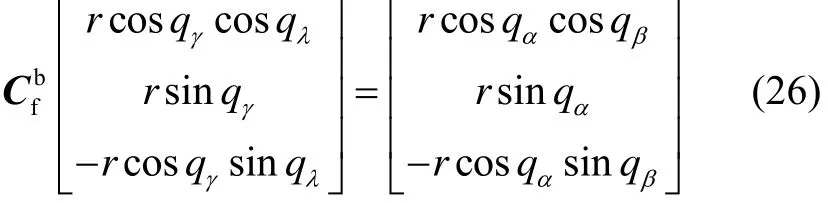
由式(26)，可以解出：

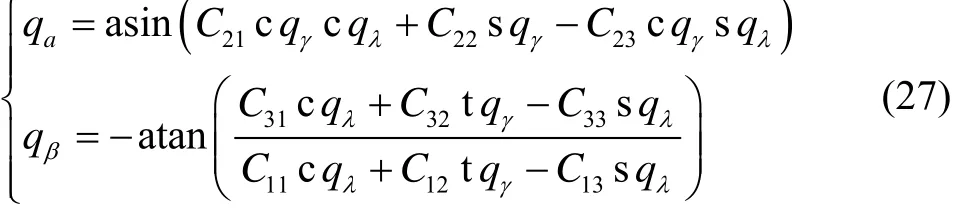
式中：Cij为从发射惯性坐标系到弹体坐标系的转换矩阵的第i行第j列元素；s、 c、t分别表示sin、cos和tan。

由此，可得系统的量测方程为

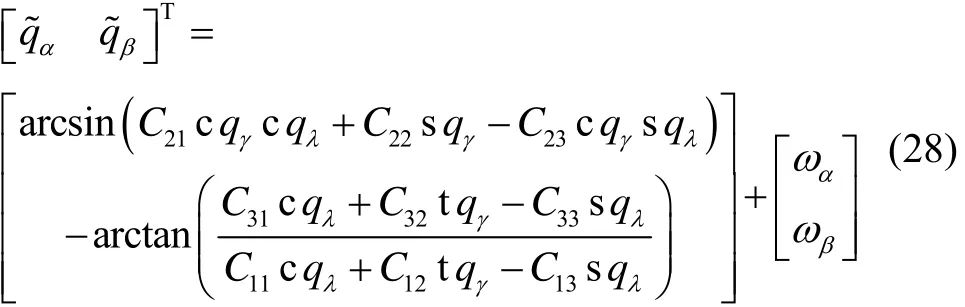
式中：Cij为从发射管坐标系到弹体坐标系的转换矩阵的第i行第j列元素；ωα和 ωβ为体视线高低角的量测噪声；s、c、t分别表示sin、cos和tan。

3 滤波器设计

根据 2.2节选取的状态量和建立的状态方程(13)～(20)，计算雅克比矩阵如下：

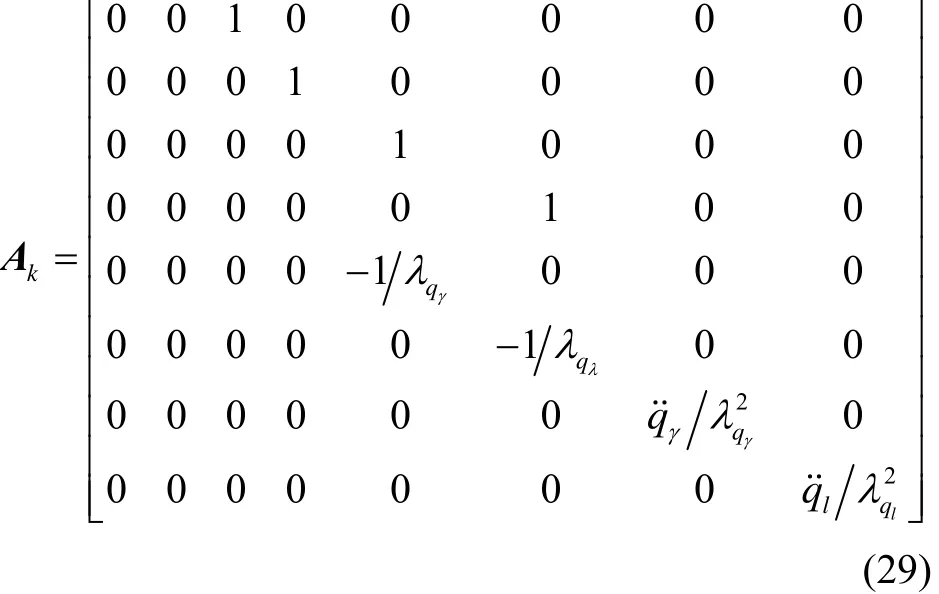
则状态转移矩阵Fk为

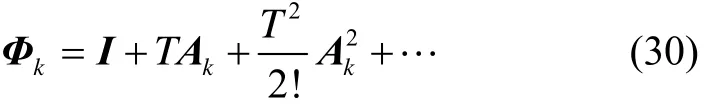
式中，T为采样周期。

然后依据式(3)和式(4)进行状态估计值和协方差阵的一步预测。再由 2.3节所建立的系统量测模型，求出系统的量测矩阵Hk为

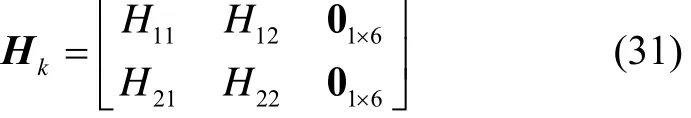
式中，

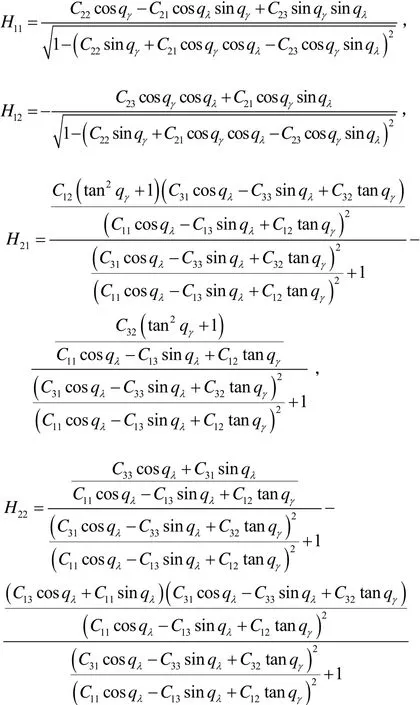
其中，Cij为从发射惯性坐标系到弹体坐标系的转换矩阵bC 的第i行第j列元素。

通过已经求解出的状态转移矩阵Fk和量测矩阵f将量测更新问题转换为求解线性回归问题，依据1.2节及1.3节所述方法，通过迭代求解出量测更新后的状态估计值和协方差阵，作为下一步滤波计算的初值。

4 仿真分析

4.1 仿真初始条件

捷联成像导引头系统量测噪声为高斯白噪声，其标准差为0.06°，然而，高斯白噪声为理想模型，实际噪声特性一般为受污染的白噪声。理想的高斯白噪声受到污染后的概率分布表达式如式(32)所示，且本文的仿真中认为污染分布也符合高斯分布，并且方差是原高斯分布的5倍。

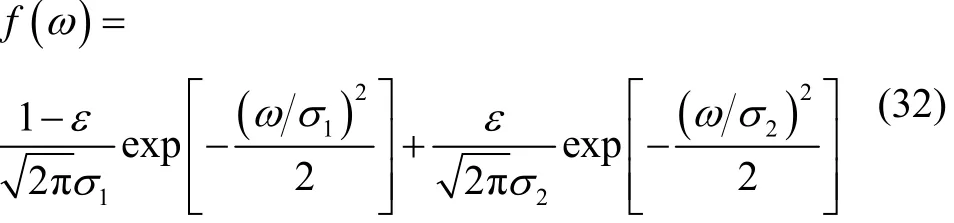
式中：ε为污染率；σ1和σ2分别为捷联成像导引头系统量测噪声标准差和污染噪声标准差。

初始弹目距离为30 km，仿真时间为20 s，目标运动特性如图3所示。

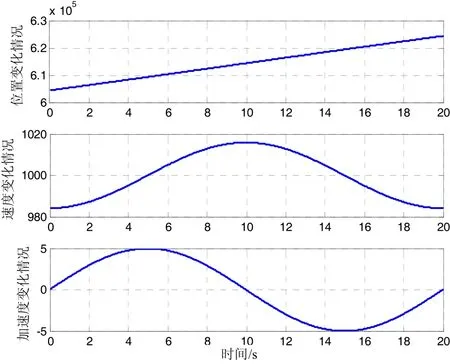
图3 目标运动特性Fig.3 Moving characteristics of target

4.2 仿真结果

取污染率ε=0.2进行仿真，得到仿真结果如图4～图8所示。图4和图5分别给出了Huber-Based滤波算法估计出的视线角和视线角速率。可以看出，该算法的视线角估计精度在0.05°以内，视线角速率估计精度在0.05 (°)/s以内，具有估计精度高、收敛速度快的特点。图7和图8分别给出了扩展卡尔曼滤波和Huberbased滤波算法的视线角估计误差和视线角速率估计误差（25次仿真的平均情况）的对比，可以看出，对于量测噪声受污染的高斯白噪声情况，Huber-Based滤波估计精度高于扩展卡尔曼滤波。

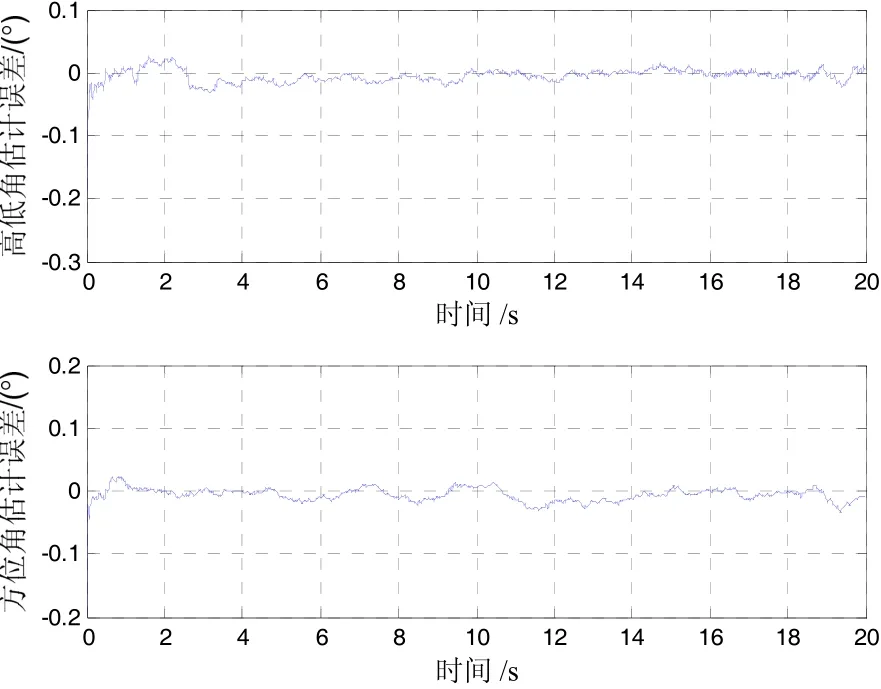
图4 视线角估计误差Fig.4 Estimation error of LOS angle

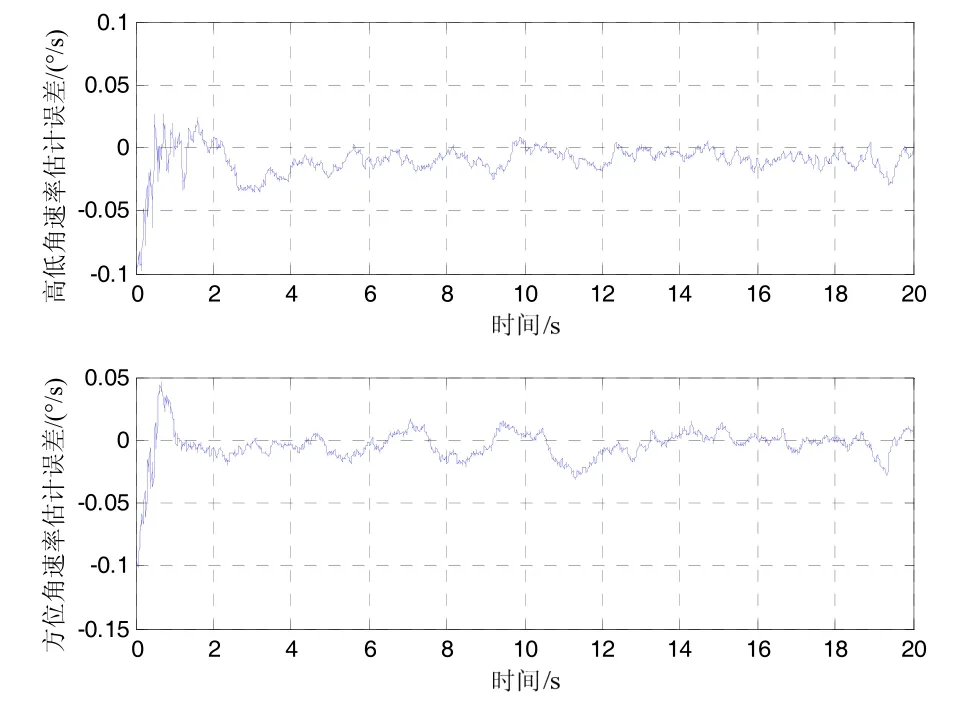
图5 视线角速率估计误差Fig.5 Estimation error of LOS rate

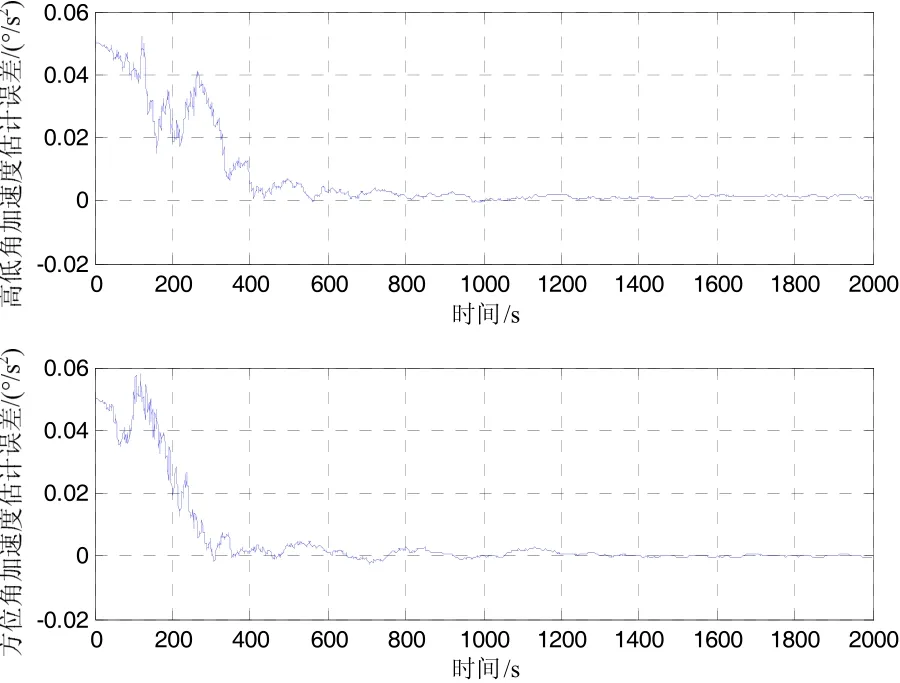
图6 视线角加速度估计误差Fig.6 Estimation error of LOS acceleration

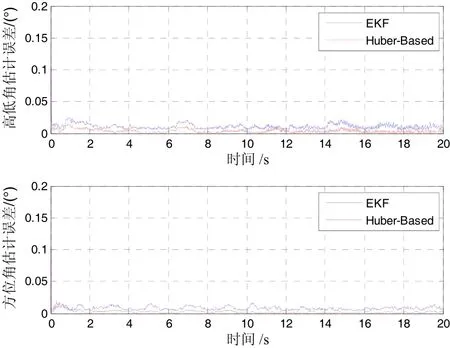
图7 两种滤波算法视线角估计误差对比Fig.7 Estimation error of LOS angle of two algorithms

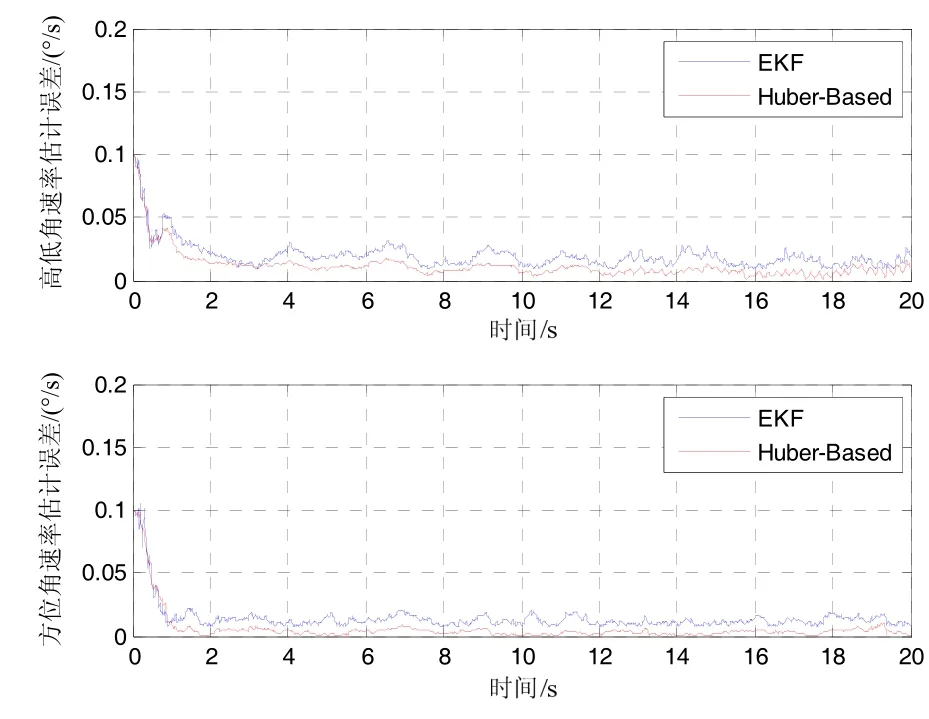
图8 两种滤波算法视线角速率估计误差对比Fig.8 Estimation error of LOS rate of two algorithms

5 结 论

本文研究捷联成像导引头系统输出的量测噪声不符合理想高斯分布时，进行视线角、视线角速率以及视线角加速度估计的方法，将 Huber-based滤波应用于捷联成像导引头视线角及视线角速率估计，有效地估计出了视线角、视线角速率以及视线角加速度。与扩展卡尔曼滤波相比，在导引头设备输出为受污染的高斯分布时，该估计方法具有一定的鲁棒性。

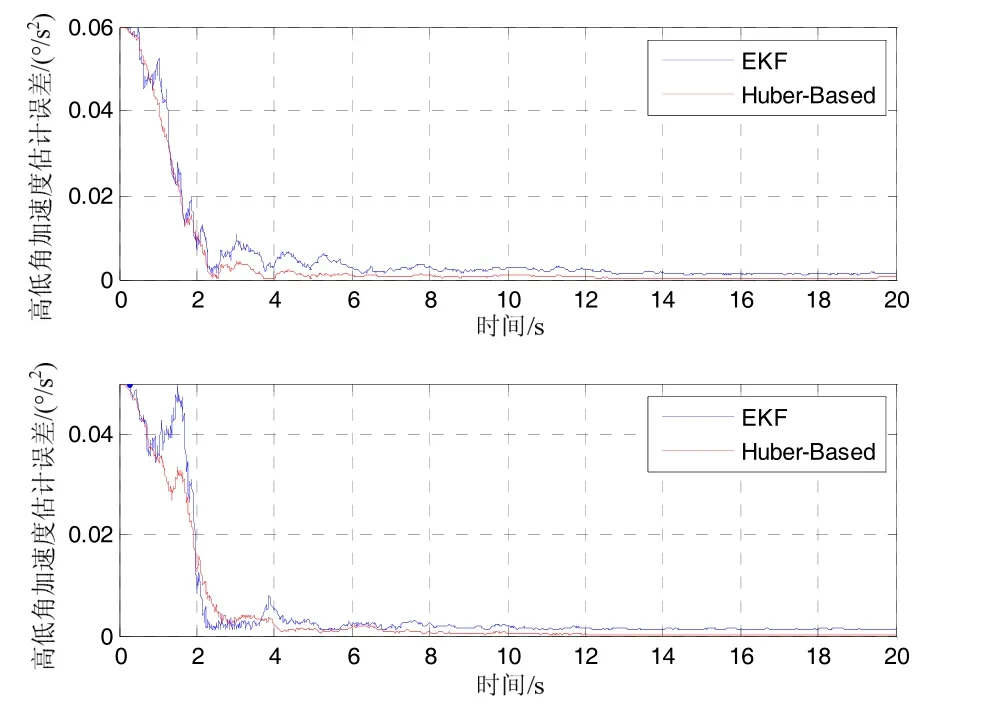
图9 两种滤波算法视线角加速度估计误差对比Fig.9 Estimation error of LOS acceleration of two algorithms

（References）：

[1] Mirmina S A. The ballistic missile defense system and its effects on the outer space environment[J]. J. Space L, 2005, 31: 287-297.

[2] Arcus P. American national missile defense system[J]. Space Policy, 2003, 19(1): 7-13.

[3] Nazaroff G. An optimal terminal guidance law[J]. IEEE Transactions on Automatic Control, 1976, 21(3): 407-408.

[4] Ehrich R D, Vergez P. Strapdown seeker technology for the terminal guidance of tactical weapons[C]//11th International Conference on Control, Automation and Systems. 2011: 969-972.

[5] 楚德强. 某型导弹捷联末制导律设计及制导精度分析[D]. 西北工业大学, 2007. Chu De-qiang. A certain type of missile strapdown terminal guidance law design and guidance accuracy analysis[D]. Northwestern Polytechnical University, 2007.

[6] 王佩, 张科, 吕梅柏. 跟踪-微分器在全捷联制导中的应用分析[J]. 西北工业大学学报, 2014, 32(5): 817-821. Wang Pei, Zhang Ke, Lv Mei-bai. The analysis of the application of tracking-differentiator in strapdown guidance[J]. Journal of Northwestern Polytechnical University, 2014, 32(5): 817-821.

[4] Wen Shi-ping, Zeng Zhi-gang, Huang Ting-wen. Reliable H∞filtering for neutral systems with mixed delays and multiplicative noises[J]. Signal Processing, 2013, 94(1): 23-32.

[5] Sangsuk S, Bullock T E. Analysis of discrete-time Kalman filtering under incorrect noise covariances[J]. IEEE Transactions on Automatic Control, 1990, 35(12): 1304-1309.

[6] Chai Qiang-long, Bai Yu-long, Dong Cun-hui. Radar target tracking error research using Kalman filter-based algorithms[J]. Applied Mechanics and Materials, 2013, 239: 1184-1187.

[7] Pedro B,Carlos S, Paulo O. Partial attitude and rate gyro bias estimation: Observability analysis, filter design, and performance evaluation[J]. International Journal of Control, 2011, 84(5): 895-903.

[8] Julier D S, Uhlmann J, Durrant-Whyte H F. A new method for the nonlinear transformation of means and covariances in filters and estimators[J]. IEEE Transactions on Automatic Control, 2000, 45(3): 2253-2261.

[9] Xiong K, Zhang H Y, Chan C W. Performance evaluation of UKF-based nonlinear filtering[J]. Automatica, 2006, 42: 261-270.

[10] 周朝霞, 任家栋, 曾庆双, 等. 测量最小分辨率特性下自主相对导航设计方法[J]. 哈尔滨工业大学学报, 2015, 47(3): 49-53. Zhou Chao-xia, Ren Jia-dong, Zeng Qing-shuang, et al. Autonomous relative navigation constrained by microwave radar minimum measure resolution[J]. Journal of Harbin Institute of Technology, 2015, 47(3): 49-53.

[11] 任家栋, 曾庆双, 丰保民. 基于地平仪两轴姿态测量的卫星自主相对导航[J]. 中国惯性技术学报, 2015, 23(5): 597-601. Ren Jia-dong, Zeng Qing-shuang, Feng Bao-min. Autonomous relative navigation with two-axis attitude measurements only infrared earth sensor[J]. Journal of Chinese Inertial Technology, 2015, 23(5): 597-601.

[7] 李璟璟, 伊国兴, 张迎春. 基于粒子滤波的捷联成像导引头视线角速率估计[J]. 弹箭与制导学报, 2009, 29(2): 91-94. Li Jing-jing, Yi Guo-xing, Zhang Ying-chun. Strapdown imaging seeker LOS rate estimation based on particle filter [J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2009, 29(2): 91-94.

[8] 宋建梅, 郑建强. 平方根滤波在捷联寻的制导系统中的应用研究[J]. 北京理工大学学报, 2006, 26(6): 476-478. Song Jian-mei, Zheng Jian-qiang. Application of H∞square root filter for strapdown homing guidance system [J]. Transactions of Beijing Institute of Technology, 2006, 26(6): 476-478.

[9] 李全运, 宋建梅. 捷联寻的制导系统滤波器设计[J].兵工学报, 2005, 26(2): 216-219. Li Quan-yun, Song Jian-mei. Strapdown homing guidance system filter design[J]. Acta Armamentarii, 2005, 26(2): 216-219.

[10] Huber P J. Robust estimation of a location parameter[J]. Annuals of Mathematical Statistics, 1964, 3(2): 73-101.

[11] Petrus P. Robust Huber adaptive filter[J]. IEEE Transactions on Signal Processing, 1999, 47(4): 1129-1133.

[12] Kumar T A, Rao K D, Swamy M N S. A robust technique for multiuser detection in non Gaussian channels[C]//The 2004 47th Midwest Symposium on Circuits and Systems. 2004: 247-250.

Line-of-sight angular-rate estimation of strapdown seeker based on robust filter

WANG Xiao-gang1, HU Zhi-yong2, YU Yang3, QIN Wu-tao1

(1. Department of Astronautics, Harbin Institute of Technology, Harbin 150001, China; 2. Dalian Communication Sergeant School of Air Force, Dalian 116600, China; 3. State-owned No.624 Factory, Harbin 150001, China)

In view of the problem that strapdown seeker can’t directly access to the line-of-sight (LOS) angular velocity, the application of robust filter in LOS rate estimation of exo-atmospheric vehicle is studied. In order to establish a nonlinear filtering estimation model, the first-order Markov model state equation is established based on the slowly varying properties of LOS rate. The LOS rate decoupling model is derived as the measurement equation. In view that some factors in the practical application can cause the noise be inaccurate in statistical properties, this paper discusses the Huber-based robust filtering method and designs the LOS rate filter. The simulation based on Huber-Based filter and extended Kalman filter is completed under the condition of non-Gaussian noise. Simulation results show that the LOS angle, LOS rate and LOS acceleration estimation precisions based on Huber-based filter method reach 0.1140′, 0.1423′/s, 0.0203′/s2, respectively, but the LOS angle, LOS rate and LOS acceleration estimation precisions based on an extended Kalman filter method only reach 0.6577′, 0.6415′/s, 0.0979′/s2, respectively. These prove that the method can effectively estimate the relative LOS rate information, and can also obtain higher estimation precision under the condition of non-Gaussian noise, showing its good robustness.

strapdown seeker, LOS Rate, first-order Markov model, nonlinear filter, Huber-based filter

V249.32

A

1005-6734(2016)02-0251-06

10.13695/j.cnki.12-1222/o3.2016.02.021

2016-01-13

2016-03-30

国家自然科学基金（61304236）

王小刚（1980—），男，副教授，研究方向为非线性滤波理论及应用。E-mail: wangxiaogang@hit.edu.cn