海洋重力辅助导航系统的系泊对准算法

祝燕华，蔡体菁，王立辉

（东南大学 仪器科学与工程学院，南京 210096）

海洋重力辅助导航系统的系泊对准算法

祝燕华，蔡体菁，王立辉

（东南大学 仪器科学与工程学院，南京 210096）

捷联惯导系统在系泊条件下的初始对准是海洋重力辅助导航实用化的关键问题之一，本质上属于三轴姿态确定问题。基于惯性凝固假设，构建了船载捷联惯导系泊对准模型，研究了传统三轴姿态确定双矢量算法。对双矢量算法进行改进，提出了一种基于加权矢量和三轴姿态确定的系泊对准算法，该算法利用两个观测矢量的误差标准差构建加权系数，生成了精度更高的基准矢量，从而提高系泊对准的精度，并且该算法只需进行一次三轴姿态解算，保持了计算量小、耗时短的特点。数值仿真和船载试验结果表明，改进后的系泊对准算法在保证初始对准快速性的前提下有效提高了对准精度，两个水平姿态角误差小于4′，航向角误差在10′左右，满足海洋重力辅助导航系统的应用需求。

捷联惯导；重力；系泊对准；三轴姿态确定

惯性导航是海上运载体最主要的导航方式之一，具有不依赖外界信息、隐蔽性好、抗辐射性强、全天候等优点，是完全自主的导航。由于惯性传感器的精度约束，惯导系统必须借助于其他导航方式的辅助才能长时间使用。重力辅助导航是利用重力特征传感器测量的重力异常信息或重力梯度信息，与重力场特征图匹配来修正惯导误差的方法，保证了导航的无源性、抗干扰和长航时，脱离了GPS的限制，具有重要的工程应用价值[1-2]。

捷联惯导系统在系泊条件下的初始对准是海洋重力辅助导航实用化的一个关键问题，本质上属于三轴姿态确定（Triaxial attitude determination，TRIAD）。TRIAD算法是通过两个不相交向量在两个坐标系中的已知坐标来确定姿态矩阵，即双矢量定姿。在静基座条件下，通常利用加速度计和陀螺仪测量的地球重力加速度和地球自转角速度作为双矢量。而当载体处于系泊状态时，由于摇摆运动的干扰，该方法不再适用。文献[3-5]引入惯性凝固假设，提出了一种基于重力加速度的对准方法，隔离了载体的摇摆运动，进而应用TRIAD算法来实现系泊对准。

本文构建了捷联惯导系泊对准的模型，研究了基于传统TRIAD的系泊对准算法。为了提高系泊对准的精度，对TRIAD算法进行了改进，提出了一种基于加权矢量和的TRIAD算法，该算法利用两个观测矢量的误差标准差构建加权系数，构造新的基准矢量，从而提高基准矢量的精度。通过数值仿真和船载试验对改进算法进行了验证，结果表明，基于加权矢量和的系泊对准算法在保证计算快速性的前提下有效提高了对准精度。

1 捷联惯导系泊对准模型的构建

1.1 坐标系描述

1）地心惯性坐标系（i）：原点位于地球中心，oxi、oyi轴在赤道平面内，oxi轴指向春分点，ozi轴指向地球极轴；

2）地球坐标系（e）：原点位于地球中心，oxe轴通过零子午线，oze轴指向地球极轴；

3）导航坐标系（n）：原点位于载体重心，oxn轴指向东（E），oyn轴指向北（N），ozn轴指向天顶（U）；

4）载体坐标系（b）：原点位于载体重心，oxb轴指向载体横轴方向，oyb轴指向载体纵轴方向，ozb轴指向载体竖轴方向；

5）载体惯性坐标系（b0）：在初始对准的起始时刻将载体坐标系b经惯性凝固后的坐标系。

1.2 系泊对准模型

根据姿态矩阵的链式法则，任意时刻载体的姿态矩阵可由下式确定[3-6]：

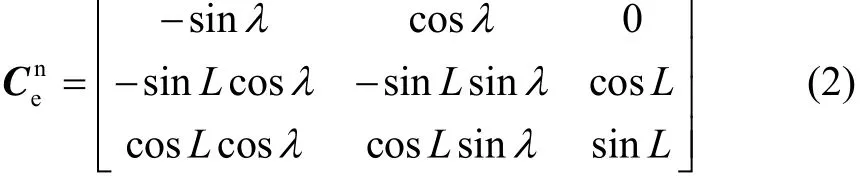
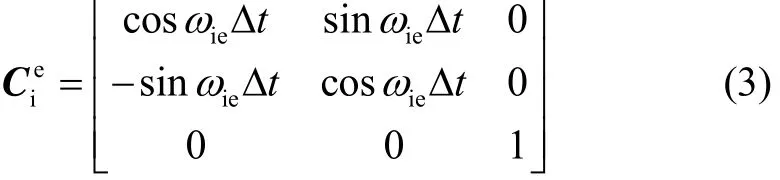
2 双矢量定姿算法

2.1 基于TRIAD的系泊对准算法

已知参考坐标系下两条非平行单位矢量为 W1和W2，它们在本体坐标系下对应的单位矢量为V1和V2。以（W1, V1）为基准矢量，分别在参考坐标系和本体坐标系中构建两组符合右手准则的正交坐标系，两组正交坐标系中各坐标轴的单位矢量分别为[7-11]

由上述分析可知，TRIAD算法采用的是双矢量定姿，那么，确定系泊对准中的常值矩阵的关键在于寻求合适的双矢量。

系泊条件下，捷联惯导系统加速度计输出的比力为

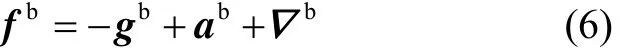
则该比力在载体惯性坐标系内的投影可表示为

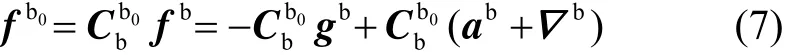
为了消除载体干扰加速度的影响，在时间段[t0,t]内对式(7)进行积分可得：

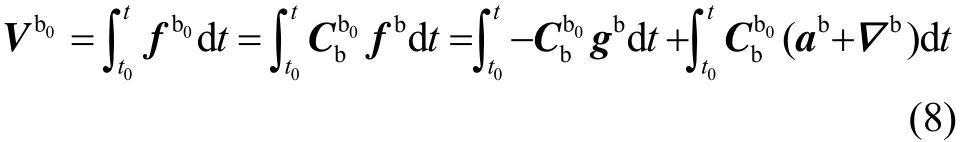
由于干扰加速度近似呈周期性变化，经过一个周期的积分近似为零，即

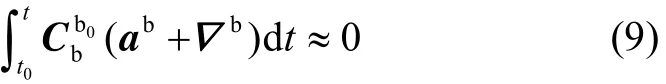
结合式(8)和式(9)可得：

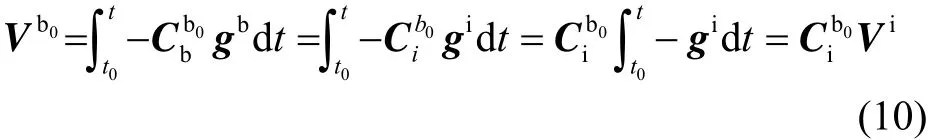
式(10)中，惯性坐标系下的重力加速度 gi与时间相关，可表示为

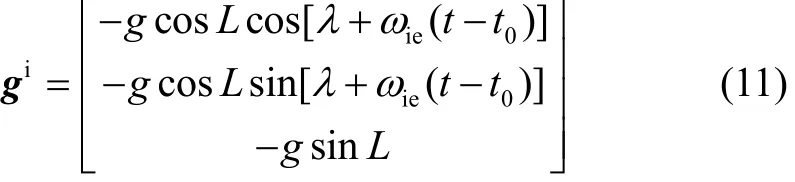
故

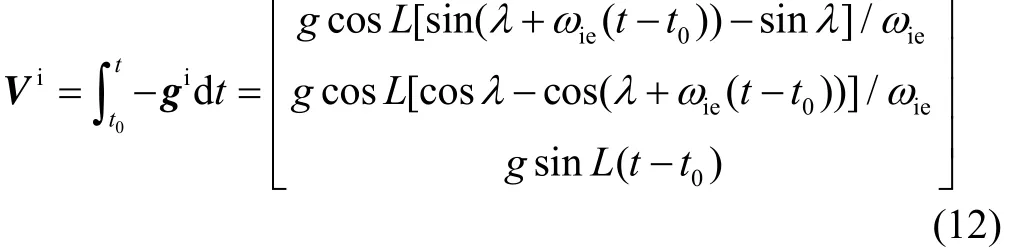
由式(10)可知，选取不同的积分时刻t1和可分别得到i系和b0系下的两组矢量则可依据 TRIAD算法求出常值矩阵进而通过式(1)获得姿态矩阵完成捷联惯导系统的系泊对准。

2.2 基于加权矢量和TRIAD的系泊对准算法

根据 TRIAD算法的原理，提高基准矢量的精度便可提高姿态矩阵解算的精度。

假设一个由两个传感器组成的系统，给定参考坐标系下两矢量W1和W2。第1个传感器观测参考坐标系下的 W1，得到观测矢量为 V1，测量误差的标准差为σ1；第2个传感器观测参考坐标系下的W2，得到观测矢量为V2，测量误差的标准差为σ2。

定义两个观测矢量的加权系数为

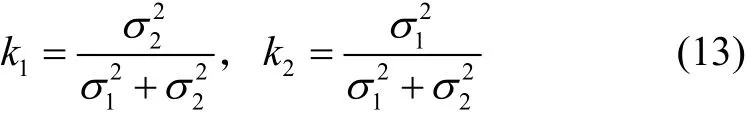
显然，最优估计误差的方差为

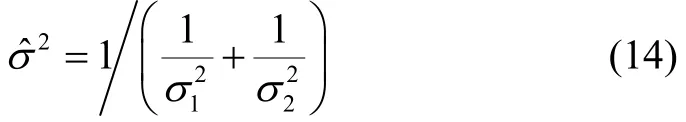
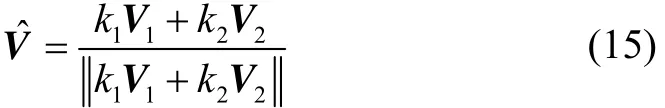
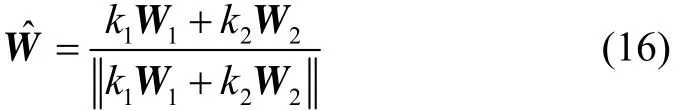
3 数值仿真研究

给定参考坐标系下两矢量W1和W2，以及参考坐标系和本体坐标系之间的姿态矩阵真值A，假设：

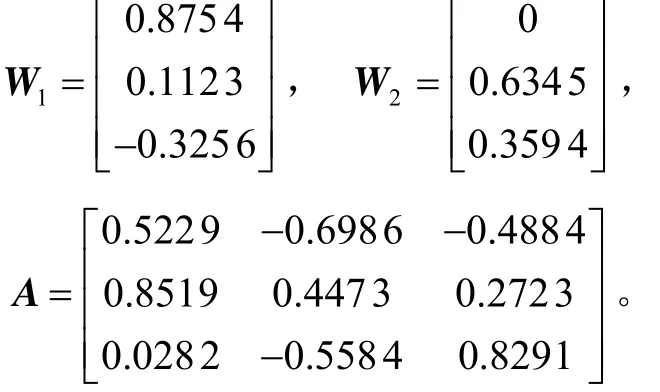
若传感器没有测量误差，则本体坐标系中对应的两个矢量应为

而实际传感器均存在测量误差，假设其服从零均值高斯分布，仿真分为如下两种情况：

1）两传感器等精度情况

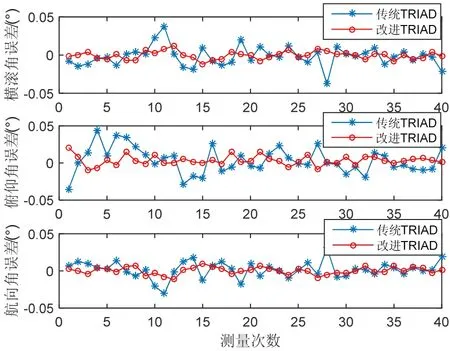
图1 等精度情况下姿态角误差比较Fig.1 Comparison on attitude errors when with equal accuracy

2）两传感器非等精度情况

由图1和图2可知，加权矢量和TRIAD算法明显提高了姿态解算的精度。仿真中选取若干不同的参考矢量和姿态矩阵真值，以及改变两观测传感器的精度，能得到多组仿真结果。精度比较情况与上述相仿，限于篇幅不再列出。

加权矢量和TRIAD算法较之传统的TRIAD算法同样只需进行一次 TRIAD解算，保持了计算量小、耗时短的特点，非常适用于进行系泊对准。

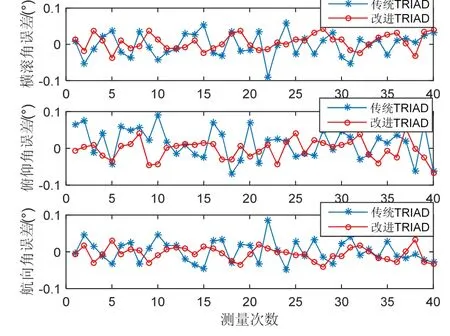
图2 非等精度情况下姿态角误差比较Fig.2 Attitude error comparison under condition of unequal accuracy

4 船载试验结果

为了验证基于加权矢量和TRIAD系泊对准算法的工程实用性，于2015年6月在山东青岛进行了4次激光捷联惯导系统船载试验。其中：激光陀螺仪精度为0.01 (°)/h，加速度计精度为1×10-5g；系泊对准时间设置为120 s，其中，t1=60 s，t2=120 s。试验中配置高精度的惯导系统作为对比基准，系统在船体内的安装情况如图3所示。表1给出四次船载试验的系泊对准结果。

由表1可知，基于加权矢量和的系泊对准算法能在载体处于摇摆基座情况下实现系统的初始对准，两个水平姿态角误差小于4′，航向角误差在10′左右，达到了初始对准的要求。

图3 船载试验系统安装情况Fig.3 System installation in shipboard experiment

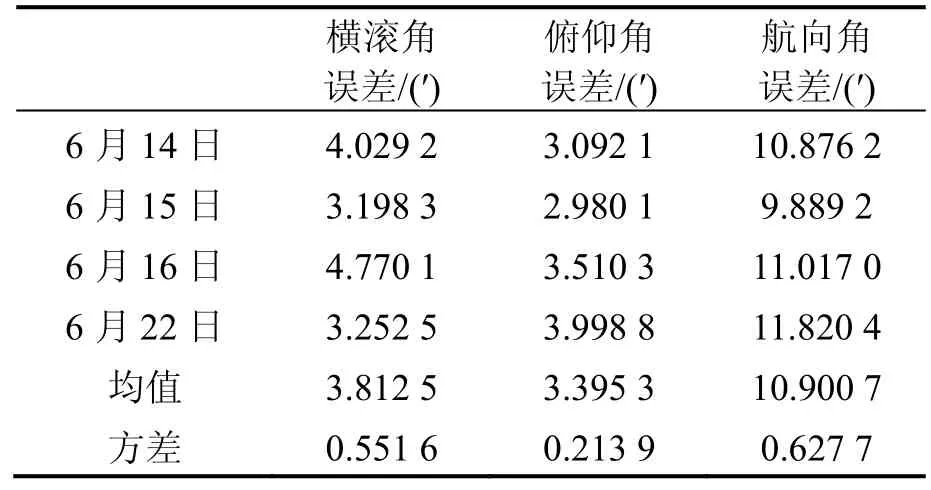
表1 激光捷联惯导系统系泊对准试验结果Tab.1 Result of mooring alignment experiment of laser SINS

5 结 论

系泊条件下的初始对准是海上运载体捷联惯导系统的关键技术之一，本文基于惯性凝固假设，构建了系泊对准模型，隔离了载体的摇摆运动，提出了一种基于加权矢量和的 TRIAD算法实现初始三轴姿态解算。该算法的优点在于利用了观测矢量的误差标准差构建了加权系数，生成了精度更高的基准矢量，提高了系泊对准的精度。由于该算法只需完成一次TRIAD解算，仍然具有计算量小、耗时短的特点，保证了系泊对准的快速性。

综上，基于加权矢量和的TRIAD算法能在保证计算快速性的前提下有效提高对准精度，满足海洋重力辅助导航系统的应用需求，具有一定的理论和工程应用价值。

（References）：

[1] Rice H, Mendelsohn L, Aarons R, et al. Next generation marine precision navigation system[C]//IEEE 2000 Position Location and Navigation Symposium. 2000: 200-206.

[2] Cai Ti-jing. Study on novel gravity passive navigation system[J]. Journal of Southeast University (Eng. Ed.), 2006, 22(1): 53-58.

[3] 秦永元, 朱新颖, 赵长山, 等. 舰载机捷联惯导自对准方案设计与仿真[J]. 中国惯性技术学报, 2008, 16(1): 28-33. Qin Yong-yuan, Zhu Xin-ying, Zhao Chang-shan, et al. Design and simulation on SINS self-alignment for carrier born aircraft[J]. Journal of Chinese Inertial Technology, 2008, 16(1): 28-33.

[4] 孙伟, 孙枫, 杨琳. 摇摆基座下捷联系统快速初始对准研究[J]. 系统仿真学报, 2013, 25(3): 495-498. Sun Wei, Sun Feng, Yang Lin. Research on rapid alignment of SINS with swaying motion[J]. Journal of System Simulation, 2013, 25(3): 495-498.

[5] 杨晔, 毋兴涛, 杨建林, 等. 方位捷联平台重力仪分布式 Kalman滤波初始对准算法[J]. 中国惯性技术学报, 2014, 22(2): 191-194. Yang Ye, Wu Xing-tao, Yang Jian-lin, et al. Distributed Kalman filter initial alignment algorithm for azimuth strapdown platform gravimeter[J]. Journal of Chinese Inertial Technology, 2014, 22(2): 191-194.

[6] Acharya A, Sadhu S, Ghoshal T K. Improved self-alignment scheme for SINS using augmented measurement[J]. Aerospace Science and Technology, 2011, 15(2): 125-128.

[7] 江洁, 王英雷, 张广军. 一种改进的基于双矢量观测的姿态确定算法[J]. 北京航空航天大学学报, 2012, 38(8): 992-995. Jiang Jie, Wang Ying-lei, Zhang Guang-jun. Improved determination algorithm using two vector measurements [J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(8): 992-995.

[8] 刘晓辉, 党亚民, 王潜心, 等. 双基线姿态确定三种算法的比较分析[J]. 大地测量与地球动力学, 2013, 33(1): 123-127. Liu Xiao-hui, Dang Ya-min, Wang Qian-xin, et al. Analysis of three algorithm of attitude determination based on two baselines[J]. Journal of geodesy and geodynamics, 2013, 33(1): 123-127.

[9] Shuster M D. The optimization of TRIAD[J]. The Journal of the Astronautical Sciences, 2007, 55(2): 245-257.

[10] Bar-Itzhack I Y, Harman R R. Optimized TRIAD algorithm for attitude determination[J]. Journal of Guidance, Control and Dynamics, 1997, 20(1): 208-211.

[11] Celik O, Hajiyev C. A comparison of attitude determination methods for small satellites[C]//Proceedings of 6th International Conference on Recent Advances in Space Technologies. 2013: 261-264.

Mooring alignment algorithm for marine gravity aided navigation system

ZHU Yan-hua, CAI Ti-jing, WANG Li-hui

(Department of Instrument Science & Engineering, Southeast University, Nanjing 210096, China)

The initial alignment of SINS in mooring conditions is a key problem to the practicability of marine gravity aided navigation system, which is essentially a three-axis attitude determination (TRIAD) problem. This paper built up a shipboard SINS mooring alignment model based on inertial freezing hypothesis, and improved the two-vector attitude determination algorithm based on the study of traditional one, which is an mooring alignment algorithm based on weighted vector and TRIAD. In the new algorithm, the standard deviation of two observation vectors is utilized to construct the weighting coefficients and generate a higher precision reference vector. Thereby, the accuracy of mooring alignment is improved. The algorithm requires just one times of TRIAD calculation, so the system keeps the advantages of small computation amount and short time-consuming. Numerical simulation and shipboard experiment results show that the weighted vector TRIAD algorithm effectively improves the alignment accuracy without decreasing the rapidity of the initial alignment. The horizontal attitude error is less than 4′, and the heading angle error is about 10′, which meet the application requirements of marine gravity aided navigation system.

strapdown inertial navigation; gravity; mooring alignment; triaxial attitude determination

U666.1

A

1005-6734(2016)02-0160-04

10.13695/j.cnki.12-1222/o3.2016.02.004

2015-09-30；

2016-04-12

国家自然科学基金资助项目（61503077）；江苏省自然科学基金资助项目（BK20130628）

祝燕华（1980—），女，副教授，从事惯性导航和组合导航技术研究。E-mail: zhuyh@seu.edu.cn