一种基于在线序贯极限学习机的大型舰船甲板态势预测方法

刘锡祥，宋 清，司马健，黄永江，杨 燕

（1. 微惯性仪表与先进导航技术教育部重点实验室，南京 210096；2. 东南大学 仪器科学与工程学院，南京 210096）

一种基于在线序贯极限学习机的大型舰船甲板态势预测方法

刘锡祥1,2，宋 清1,2，司马健1,2，黄永江1,2，杨 燕1,2

（1. 微惯性仪表与先进导航技术教育部重点实验室，南京 210096；2. 东南大学 仪器科学与工程学院，南京 210096）

在舰船摇荡运动无法有效抑制时，可利用惯性导航系统实时测量甲板运动，并利用甲板运动的当前以及历史数据对未来时刻的甲板运动进行预测，以提高舰载机的起降安全性。然而甲板摇荡运动作为风浪、潮汐等共同作用的产物，具有较强的非线性、随机性和时变性。针对上述特性，引入具有信息实时更新功能的在线序贯极限学习机（OS-ELM）方法对甲板运动态势进行预测。该方法通过实时更新参与模型解算的样本数据，具有计算量小、学习映射能力强的优点。针对OS-ELM中存在的隐含层节点个数选择，以及甲板态势预测中出现的样本个数、历史数据长度等参数选择问题，引入遗传算法（GA）进行寻优。基于模拟甲板摇荡数据的仿真表明，该预测方法可以实时跟踪甲板运动的实时性变化，并对甲板运动态势进行预测。

甲板态势预测；在线序贯极限学习机；信息更新；遗传算法

航空母舰作为舰载机的起降平台，其甲板运动是影响舰载机着舰安全的一个重要因素[1-2]。由于风浪的激励，在海上航行的航母会产生六自由度的摇荡运动，摇荡运动将导致舰载机的理想着舰点为三维空间中的活动点[1-2]。理想着舰点位置的变化，特别是由纵摇与升沉耦合形成的理想着舰点高度的变化，将大大增加舰载机的着舰难度，甚至使其不能着舰[1-2]。为了保证舰载机的着舰安全性，需要对舰船的六自由度运动进行控制，使甲板运动处于一个理想范围内。然而在舰船六自由度摇荡运动中，除横摇与航向可一定程度上通过舵鳍联合控制外，对其它的运动，尤其是垂荡（及垂荡引起的升沉）尚无有效地抑制方法[3]。当前条件下，比较现实和有效的方法是对舰船的摇荡运动进行实时测量，并利用当前和历史摇荡数据对未来一段时间内的甲板运动进行预测，以保证舰载机的起降安全性[2,4]。

对舰船姿态极短期预测技术的研究已久，从理论分析到模型建立、再到实船验证，国内外均取得许多研究成果，如统计预报法、卷积法、Kalman滤波法、周期图法、艏前波法、功率谱自相关法等[5-7]。这些研究成果在船舶优化设计、适航性/安全性评估等方面得到广泛应用。上述各方法一般基于两点：一是运动力学模型；二是舰船响应谱模型。但是舰船兴波响应关系复杂，模型求解困难，其对海浪的观测（即模型输入）较为困难，很难适用于以舰载机起降为目的的实时甲板态势预报中。

针对模型方法的不足，国内外业者提出基于时间序列、神经网络、灰色预测等甲板态势预测方法，均取得了较好的成果，其中以神经网络及其改进方法最为典型[8-11]。基于机器学习的神经网络具有建模简单、非线性映射能力强等诸多优点，预测提前量可达到5～7 s。但经典神经网络存在网络训练时间长、在线调整困难等不足，难以解决甲板态势预测中甲板运动的时变性、非线性、不规则等诸多问题。与此同时，上述诸方法还存在预测时间短的不足。文献[11]分析指出，舰载飞机自动着舰系统需要在着舰前10～13 s时间内加入甲板运动补偿信息，即对甲板运动态的预报提前量应为10～13 s。

针对经典神经网络的不足，Huang等提出了一种新的SLFN算法—极限学习机（ELM）[12-17]。该算法不依赖于输入权值和隐单元偏置的选择，可进行随意赋值，然后通过合适的激活函数得到隐含层的输出矩阵，从而网络的输出权值可以解析获取，具有学习速度更快、泛化能力更强的优点。然而基于确定样本的ELM 同样难以解决时变甲板态势的预测问题。文献[17]结合序列学习与ELM算法，提出了在线序列ELM（OS-ELM）算法。在方法中，数据可以一个个或一块块地添加到网络中。但该算法保留了全部的历史数据，当该方法应用于甲板态势预测时，久远的历史数据会对当前的预测模型形成干扰，降低预测精度。基于此，本文结合舰船运动的瞬时性特点，具体介绍并推导了一种使用窗口数据的OS-ELM算法。该方法可根据窗口的长度，实时丢弃历史数据并补充最新甲板运动数据，同时根据新的样本序列对网络参数进行调整，从而保证模型参数的实时性。针对OS-ELM中隐节点个数的选择，以及甲板态势预测中的样本个数、样本中历史数据的长度选择问题，引入遗传算法（GA）进行寻优。基于模拟舰船运动数据的仿真预测结果表明，OS-ELM方法可以有效地对甲板运动态势进行预测。

1 甲板运动的特性与建模

作为潮汐、风浪以及不规则气流共同作用的产物，舰船摇荡具有较强的非线性、不规则性和随机性，很难用确定的数学模型进行普适性描述[1-2,6]。因而，业者通常在某单一海况、航速下，针对某一特定舰船进行研究，以降低甲板运动模型的建模难度。20世纪50年代，丹尼尔·皮尔逊将通信理论中处理噪声的方法引入到波浪及船舶运动的研究中，提出了在随机海浪作用下船舶运动的计算方法，即基于有限多个正弦波叠加组合的船舶运动计算方法，并得到了广泛应用[1-2,4,18]。

基于正弦波组合的确定性数学模型认为处于成熟期的海浪是一个平稳随机过程，可以看作是由无数个独立随机变量叠加的过程。甲板运动作为海浪作用的产物，亦可以看作由无数个独立随机变量叠加组成。大量实测数据与统计结果表明，在确定的海况下，甲板运动可以被假设为具有窄频带的平稳随机过程，并且可用有限个不同正弦波进行叠加来简化描述这种运动。文献[1]在中等海况、航速30 kn时，对某型航空母舰的摇荡运动进行了研究，总结给出其纵摇、横摇、航向以及升沉的运动模型如下：

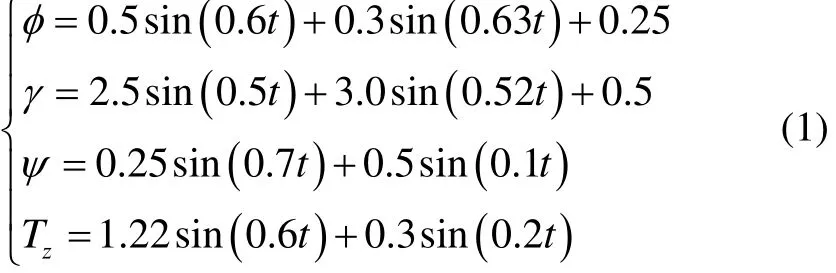
式中：φ、γ、ψ与Z分别为舰船的纵摇、横摇、航向与升沉运动，t为运动时间，其中姿态运动单位为(°)，升沉单位为m。

基于正弦波叠加的舰船运动模拟方法非常简单，但生成的曲线较为光滑。为了模拟甲板运动的时变性以及测量误差，需要添加一定的测量噪声。

2 基于OS-ELM的甲板态势预测方法

2.1 甲板态势预测的数据准备

海洋环境下，舰船的摇荡运动具有瞬时性。不考虑各运动之间的耦合因素，六自由度运动中的各项运动均为单维时间序列数据，如图1所示。甲板态势预测即根据某一摇荡运动的历史数据（包括当前数据在内）预测未来某个（或某时间段）的甲板运动情况。

图1 甲板态势预测中的样本产生过程Fig.1 Sample production for deck-motion prediction

图1中，n与N0分别为当前采集与参与训练的样本数；Δt为样本采集周期；n_num为每一样本中，用于预测的（包括当前数据在内的）历史数据；为预测时间，即预测提前量。上述各变量中，当采集的运动数据量小于时，无法构成第一个完整的训练样本。当即数据量小于时，样本量没有达到预设的参与训练样本数，无法进行网络训练；当时，可以进行网络训练与甲板态势预测；当时，需要在网络参数中去除样本的信息，并添加当前样本的信息。

2.2 基于OS-ELM的甲板态势预测算法

2.2.1 OS-ELM基本原理及预测模型

给定N0个不同样本时，其中表示样本输入表示样本期望输出，具有L个隐层神经元的单隐层前向神经网络的输出函数表达式为[12-17]：

式中：ai和bi为隐层节点参数；βi为连接隐节点i与输出层之间的权值。表示输入在第i个隐节点的输出。

令神经网络的实际输出与期望输出相等，有：

式中：

随机选择隐层节点参数ai和bi，则隐层输出矩阵为已知值。神经网络的训练问题转化为求解线性方程中的权值 β0。注意到多数实际应用中，隐含层节点数不大于样本数，即，式(3)中方程数大于未知数，可通过最小二乘法求解权值β0，从而有：

在获取到前向神经网络所有参数ai、bi及 ˆβ后，可以使用下式进行预测：

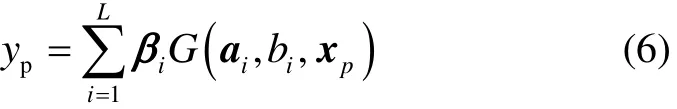
式中：xp用于预测的历史数据，yp根据模型及输入得到的预测值。

2.2.2 OS-ELM实时信息删除过程

在获取新的信息后，需要及时剔除旧的训练样本信息，并保证参与构建网络的模型样本数始终为N0。注意到式(5)在求解过程中，需要进行矩阵求逆运算为一个L×L维矩阵，在隐节点数L较大时，求逆运算量较大。OS-ELM实时信息更新过程中，若按照式(4)与(5)的求解，则需要在剔除信息以及增加信息时，重复进行L×L矩阵求逆运算，计算量大。若能在信息剔除与增加过程中，利用式(4)与(5)的中间量，则可以省却大量的数据运算。

2.2.3 OS-ELM实时信息增加过程

注意到上述中间过程存在关系式：

式(7)～(10)构成了信息更新过程中，OS-ELM网络中的相关信息删除与更新过程。

3 基于GA的OS-ELM态势预测中参数的选择

注意到第 2节中，p_num由舰载机着舰引导系统决定，而参数n_num与N0需要人工设定；第3节中前向神经网络的隐层节点数L亦需要人工设定。针对上述参数的选择尚无普适性的标准方法，一般取决于从业者的经验。本文引入遗传算法对上述参数进行寻优。遗传算法是模拟自然选择与生物进化过程的计算模型，在诸多领域得到广泛应用，其原理此处不再赘述[19]。

与其他传统的优化方法相比，GA的搜索策略不依赖梯度信息或其他辅助信息，但需要给定影响搜索方向的目标函数或适应度函数。考虑到甲板运动的周期性，摇荡数据中可能存在过零点，无法使用相对值表达预测的精度等问题。本文选择对预测误差的均值与方差进行评价，定义适应度函数如下：

式中：M为预测误差序列的均值，S为预测误差序列的方差。

基于GA的参数寻优过程如下：

步骤 1：随机生成若干组L、n_num与N0，对其进行编码生成个体，作为初始种代群；

步骤2：利用上述参数进行OS-ELM训练与预测，计算各个体的适应度J；

步骤 3：根据各个体适应度大小，进行选择性繁殖，并以交叉概率Pc进行优秀个体基因的交叉，以变异概率Pm进行优秀个体基因的变异；

步骤 4：对生成的新一代个体进行反编码，得到L、n_num与N0，并返回步骤2，重复上述过程；

步骤 5：在完成预设次数的遗传进化后，结束上述过程，并选择最优秀的个体进行反编码，得到与N0作为寻优结果。

4 试验结果与分析

4.1 仿真条件设置

以公式(1)为甲板运动模拟器，生成纵摇、横摇、航向与升沉理论运动参数，并在理论数据上分别叠加方差为0.02°与0.1 m的白噪声作为姿态角与升沉运动的实际测量数据，并假设数据采集周期为1 s。

使用GA方法对OS-ELM中隐含层节点数L、样本参数n_num与N0进行寻优，设定初始种群数目为15，交叉与变异概率分别为0.75与0.05，迭代次数为20。获取纵摇、横摇、航向与升沉的相关参数如表 1所示。表1中基于GA寻优结果表明，不同的数据所需的最优参数并不相同。

仿真过程中，设n_num为 12，即预测提前量为12 s。仿真分为两个阶段进行：① 在获取个样本后，进行基于式(3)～(5)的网络训练，并利用网络训练结果对样本进行预测；② 在样本的实时更新阶段，进行基于式(7)～(10)的网络训练，并对当前样本的下一个样本进行预测。并将上述过程分为离线与在线两个过程。

表1 基于GA寻优的甲板态势预测参数设置Tab.1 Parameters for prediction based on GA

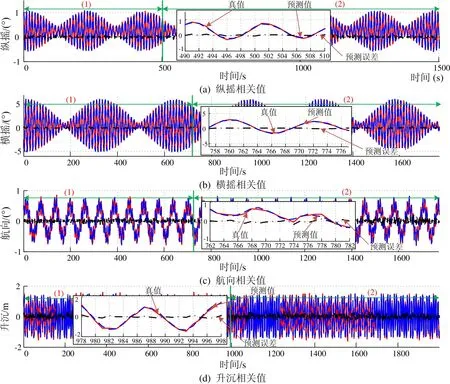
图2 甲板态势预测预测结果Fig.2 Deck-motion prediction results

4.2 仿真结果与分析

仿真过程中，由于用于训练的样本数N0以及各样本参数n_num并不相同，离线段所需的时间各不相同。为了便于后续的比较，设定用于OS-ELM在线训练及预测的时间段均为900 s。在误差分析阶段，综合考虑离线与在线两个时间段的数据误差情况。

仿真结果如图2～5所示，分别对应纵摇、横摇、航向与升沉，图中实线、虚线、点划线分别对应样本真值、预测（包括拟合）值以及预测误差，阶段①与②分别表示网络训练过程的离线与在线两个时间段。分别统计离线与在线两个时间段的预测误差，结果如表2所示。考虑到表达误差的直观性，将式(11)中关于误差均值与方差的指标与样本真值的方差进行比较，定义为表2中的“比例”。

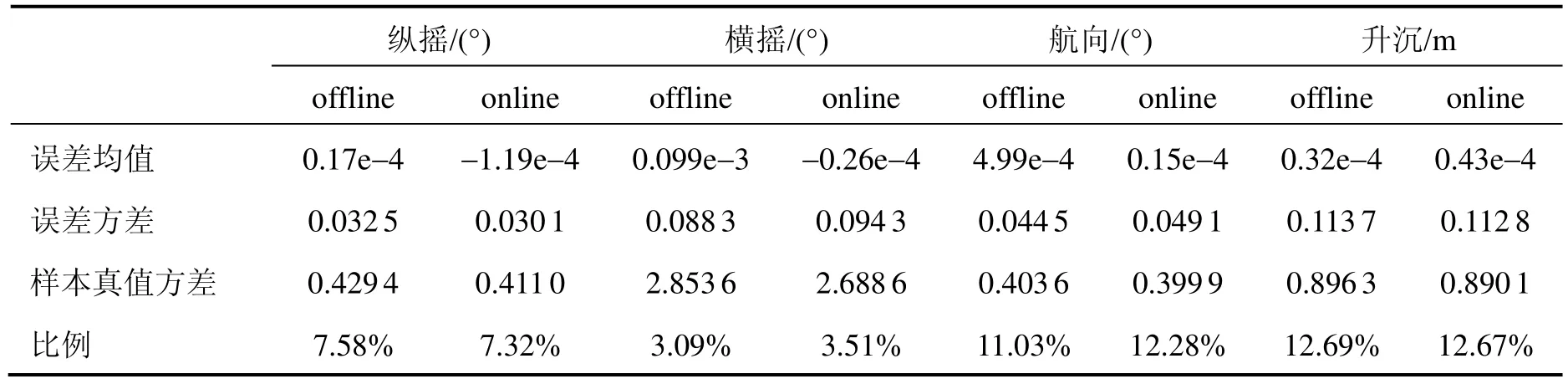
表2 预测统计结果Tab.2 Statistics of prediction results

从图2中的放大部分可以看出，预测曲线可实时跟踪样本真值的变化，预测误差小幅度振荡，无明显时延与预测误差大值。这表明，基于实时在线OS-ELM方法与GA寻优的参数可以对式(1)表示的甲板运动态势进行预测。表2与图2表明，在离线与在线两个阶段，各统计值预测误差振荡幅值类似，无明显区别。这就说明，OS-ELM的信息实时更新可以应对甲板振荡的最新变化，具有较强的适应性。

5 结 论

本文针对大型舰船甲板态势预测技术展开研究。在分析甲板运动的瞬时性、非线性与随机性后，给出了基于多个正弦波叠加组合的甲板运动模型。提出了使用 ELM 方法进行甲板态势预测，具体将基于OS-ELM 的甲板态势预测过程分解为离线阶段与实时阶段：其中离线阶段采集训练网络模型所需的各样本数据，并进行集中训练，得到网络各参数；而在线阶段实时采集样本数据，并对网络参数进行在线调整，添加新信息、删除旧信息，以应对甲板运动的瞬时性特征。

针对应用OS-ELM方法带来的隐层节点数选择，以及构建网络训练样本时的样本数、样本中历史数据长度的选择问题，本文引入GA进行参数寻优；并基于甲板运动的周期性特点定义了相应的适应度函数。仿真结果表明，该预测方法可以实时跟踪甲板运动的实时性变化，并对甲板运动态势进行预测。

（References）：

[1] John L. Automatic landing systems are here[R]. AD-2714925, 1974: 1-15.

[2] Lu K K, Cheng N, Li Q. Research and simulation on the carrier deck motion adaptive prediction for ACLS design [C]//2014 IEEE Chinese Guidance, Navigation and Control Conference. 2014: 1341-1345.

[3] 董美华, 马汝建, 赵东. 船舶减摇技术研究进展[J]. 济南大学学报, 2008, 22(2): 183-188. Dong M H, Ma R J, Zhao D. Research progress of ship anti-rolling technology[J]. Journal of University of Jinan, 2008, 22(2): 183-188.

[4] 张永花, 周鑫. 舰载机着舰点垂直运动补偿技术仿真研究[J]. 系统仿真学报, 2013, 25(4): 826-830, 838. Zhang Y H, Zhou X. Simulation study on landing point vertical motion in carrier landing[J]. Journal of System Simulation, 2013, 25(4): 826-830, 838.

[5] Chung J C, Bien Z, Kim Y S. A note on ship-motion prediction based on wave-excitation input estimation[J]. IEEE Journal of Oceanic Engineering, 1990, 15(3): 244-250.

[6] Triantafyllou M, Bodson M, Athans M, et al. Real time estimation of ship motions using Kalman filtering techniques [J]. IEEE Journal of Oceanic Engineering, 1983, 8(1): 9-20.

[7] Masi G D, Gaggiotti F, Bruschi R, et al. Ship motion prediction by radial basis neural networks[C]//2011 IEEE Workshop on Hybrid Intelligent Models and Applications. 2011: 28-32.

[8] Shen J H, Zhang C B, Li J D. The prediction of ship motion via updating MGM(1,n) model[C]//Proceedings of 2009 IEEE International Conference on Grey Systems and Intelligent Services. Nanjing, China, 2009: 533-537.

[9] 张兮龙, 叶家玮, 魏栋. 基于时间序列法的舰船运动预报实验研究[J]. 航海工程, 2008, 37(6): 13-16. Zhang X L, Ye J W, Wei D. Research on the prediction of the ship motion using time series analysis[J]. Ocean Engineering, 2008, 37(6): 13-16.

[10] 吴晞, 韩晓光, 李宇辰. 基于改进自回归模型的舰船摇荡运动短时预报[J]. 中国航海, 2014, 37(1): 112-115. Wu X, Han X G, Li Y C. Short-term forecasting of ship swaying motions based on improved AR model[J]. Navigation of China, 2014, 37(1): 112-115.

[11] 贾新强, 林鹏, 王敏文. 舰载机着舰运动误差及其补偿仿真研究[J]. 航空计算技术, 2010, 40(1): 114-118. Jia X Q, Lin P, Wang M W, et al. Study on disturbance of board movement in process of carrier aircrafts landing and its compensation[J]. Aeronautical Computing Technique, 2010, 40(1): 114-118.

[12] Huang G B, Zhu Q Y, Siew C K. Extreme learning machine: Theory and applications[J]. Neuro-computing, 2006, 70: 489-501.

[13] Huang G B, Zhou H M, Ding X J, et al. Extreme learning machine for regression and multiclass classification[J]. IEEE Transactions on Systems, Man, and Cybernetics –Part B: Cybernetics, 2012, 42 (2): 513-529.

[14] Ding S F, Xu X Z, Nie R. Extreme learning machine and its applications[J]. Neural compute & Application, 2015, 25: 549-556.

[15] Han F, Yang S X, Guan J. An effective hybrid approach of gene selection and classification for microarray data based on clustering and particle swarm optimization[J]. International Journal of Data Mining and Bioinformatics, 2015, 13(2): 103-121.

[16] Zhong H M, Miao C Y, Shen Z Q, et al. Comparing the learning effectiveness of BP, ELM, I-ELM, and SVM for corporate credit rating[J]. Neuro Computing, 2014, 128: 285-295.

[17] Yin J C, Zou Z J, Xu F. On-line prediction of ship roll motion during maneuvering using sequential learning RBF neural networks[J]. Ocean Engineering, 2013, 61: 139-147.

[18] 秦兴春, 茅坪, 卢惠民. 某型舰船主要运动姿态的模拟仿真[J]. 计算机仿真, 1998, 15(4): 49-51. Qin X C, Mao P, Lu H M. The simulation of one warship’s main motion gestures[J]. Computer Simulation, 1998, 15(4): 49-51.

[19] 程超, 穆荣军, 蔡玲, 等. 基于遭遇波的艏前波法的航母姿态预报[J]. 中国惯性技术学报, 2015, 23(3): 409-414. Cheng Chao, Mu Rong-jun, Cai Ling, et al. Doppler interpolation method based on extrapolation and CIC filter[J]. Journal of Chinese Inertial Technology, 2015, 23(3): 409-414.

Deck-motion prediction method for large ship based on online-sequence extreme-learning-machine

LIU Xi-xiang1,2, SONG Qing1,2, SIMA Jian1,2, HUANG Yong-jiang1,2, YANG Yan1,2

(1. Key Laboratory of Micro-inertial Instrument and Advanced Navigation Technology, Ministry of Education, Southeast University, Nanjing 210096, China; 2. School of Instrument Science & Engineering, Southeast University, Nanjing 210096, China)

When the swaying motions of ship cannot be effectively restrained, the deck-motion prediction could be executed based on the current and historical deck-motions measured by inertial navigation system in order to ensure the safety of carrier-based aircrafts in landing. To cope with the non-linearity, randomness and time-variant of deck-motion caused by sea-wave, tide and wind, an online-sequence extreme-learningmachine (OS-ELM) is introduced for deck-motion prediction. The new and old samples in the OS-ELM can be real-time added to and discarded from the network with strong ability in tracing the deck-motion’s changes. For selecting the number of hidden nodes in OS-ELM, the number of historical data in one sample and the number of samples, gene algorithm are adopted to search optimized parameters. The simulation based on the simulated deck-motion data indicate that the proposed method can track the deck-motion in real-time and predict the deck-motion with high accuracy.

deck-motion prediction; online-sequence extreme-learning-machine; information update; gene algorithm

U666.1

A

1005-6734(2016)02-0269-06

10.13695/j.cnki.12-1222/o3.2016.02.024

2016-01-07

2016-03-25

自然科学基金（61273056）

刘锡祥（1976—），男，博士，教授，博士生导师，研究方向为惯性导航、组合导航与信息融合技术。E-mail: scliuseu@163.com