捷联惯导系统最简多位置解析对准改进算法

丁磊香，许厚泽，王 勇，柴 华，蔡小波

（1. 中国科学院 测量与地球物理研究所 大地测量学与地球动力学国家重点实验室，武汉 430077；2. 中国科学院大学，北京 100049）

捷联惯导系统最简多位置解析对准改进算法

丁磊香1,2，许厚泽1，王 勇1，柴 华1，蔡小波1,2

（1. 中国科学院 测量与地球物理研究所 大地测量学与地球动力学国家重点实验室，武汉 430077；2. 中国科学院大学，北京 100049）

最简多位置解析对准作为测量IMU偏置的简单方法，降低了传统多位置解析对准的工程复杂度，摆脱了伺服平台的限制，但是最简多位置解析对准目前使用的是几何方法，几何方法计算复杂，精度受先验信息的影响。针对这一问题，提出了最简多位置对准解析算法，通过解析算法可得到IMU偏置的解析解。通常两位置即可求得IMU偏置，特殊情况需要三位置，某些特殊位置可以计算特定轴向的偏置。解析法计算简单，不受先验信息的影响，并通过实例仿真证实该算法的有效性，计算误差主要由一阶近似误差和测量噪声引起。

捷联惯导系统；多位置对准；解析对准；常值偏置

捷联惯导系统（SINS）初始对准的时间和精度直接影响导航系统的快速反应能力和导航解算精度[1-2]。静基座对准时，系统可观测度较低[3]，东向陀螺漂移不可观测，对准的精度和速度都会受到影响[4-5]。多位置对准技术可以估计出加速计零偏和东向陀螺漂移，提高初始对准精度[6-8]。根据使用的信息量不同，多位置对准技术可分为两类：多位置精对准和多位置解析对准。多位置精对准[9-11]使用静止和转动过程中的惯性传感器数据，采用卡尔曼滤波法估计出惯性测量单元（IMU）的偏置和姿态。多位置解析对准[12-13]只使用静止状态下惯性传感器的输出数据，根据各静止位置间的解析关系补偿掉偏置偏差。

传统多位置解析对准一般要求捷联惯导系统绕天向旋转一个或多个特定的角度，这增加了工程实现的复杂度，且伺服平台的精度会影响对准精度。文献[14]提出了最简多位置解析对准，可以克服上述困难，理论上该方法任意两位置即可解算惯性传感器的偏置，它可以作为一种简易的初始对准或现场标定的方法，并且在特殊状态下，该方法可以很好地估计出某一轴向的加速计零偏或陀螺漂移。

上述最简多位置解析对准使用的是几何方法，根据先验信息反复搜索，得到IMU偏置的几何解。几何方法计算复杂，并且先验信息对计算结果的影响较大。针对此问题，本文推导了IMU偏置的解析表达式，可以得到任意多位置IMU偏置的解析解，称之为解析方法。解析方法计算简单，不受先验信息的影响，并通过实例仿真验证了该方法的有效性。

1 任意两位置解析对准

1.1 理论分析

将当地东北天地理坐标系作为导航系（记为n系），载体坐标系记为b系，n系到b系的转换矩阵为 C。 IMU输出的三轴加速度记为，三轴角速度记为。地球自转角速度记为ω，载体所在位置的重力记为g，载体所在位置的纬度记为B。若载体处于静止状态，则有下式成立：

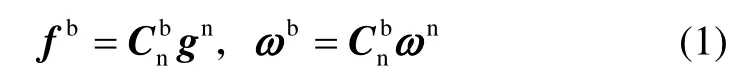
式中， fb为b的理论值， ωb为b的理论值，gn=[00 g]T，ωn=[0 ωcos Bωsin B]T。

由式(1)可得：

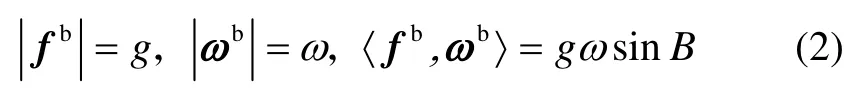
式中，||为取模运算符， 〈 〉为内积运算符。

对于多位置对准，对准时间在较短时间完成，可认为IMU偏置保持不变。偏置误差是IMU误差的主要组成部分，只考虑IMU的常值偏置误差。记三轴加速度计的常值零偏为，记三轴陀螺的常值漂移为，那么下式成立：

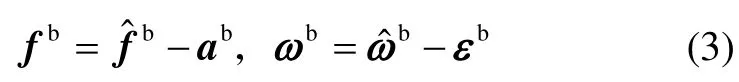
把式(3)代入式(2)可得下式：

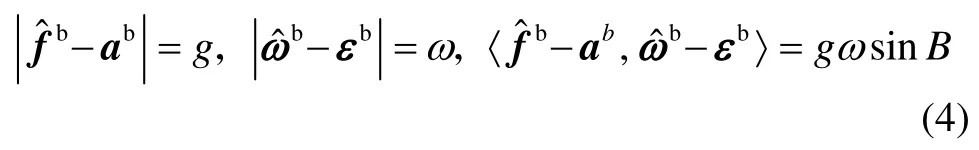
式(4)中含有6个未知数，在多位置初始对准中，每个位置可得到关于IMU偏置的三个方程，理论上两位置初始对准即可得到IMU偏置。因此如何根据上述方程求得IMU偏置是最简多位置解析对准的关键。文献[14]给出了一种求解IMU偏置的几何方法，这种方法根据先验信息反复搜索，直到搜索到满足所需精度的解，几何方法计算复杂，并且受先验信息的影响较大。本文通过研究发现，上述方程存在解析解，详细推导过程如下。

1.2 任意两位置解析对准的解析算法

式(4)第一式等号两边平方，忽略掉高阶小项，并整理，可得下式：

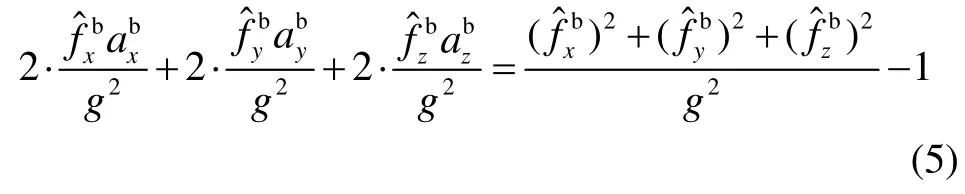
对式(4)第二式作同样的处理，可得下式：

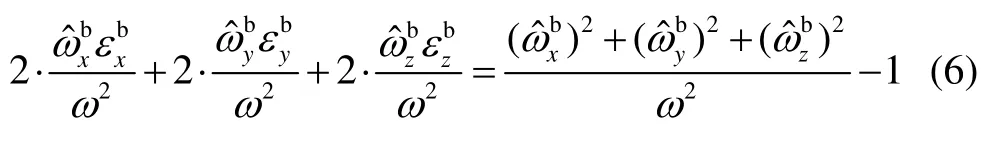
式(4)第三式等号两边同除以gω，忽略掉高阶小项，并整理，可得下式：

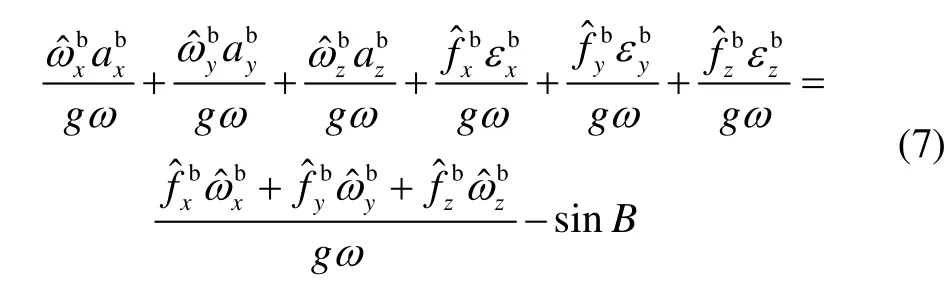
把式(5)~(7)写成矩阵的形式，可得下式：

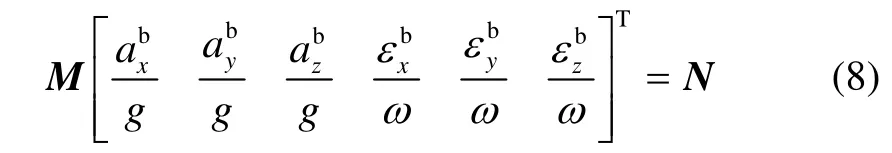
式中，

式(8)即为关于IMU偏置的解析表达式，表达式为3个六元一次方程。任意两位置可以得到6个六元一次方程构成的方程组，解此方程组可得到IMU偏置的解析解，把这种方法称为解析法。

2 实例仿真

举一仿真实例验证上述解析法的有效性，相关的仿真参数与文献[14]相同。

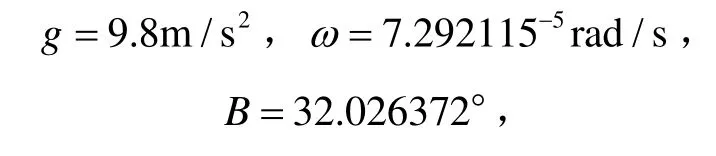
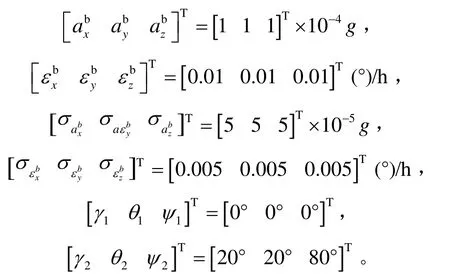
式中，σa和σε分别为加速计和陀螺的测量白噪声，

γk、θk和Ψk分别为第k（k=1, 2）个位置处的横滚角、俯仰角和航向角。

在两个位置处采集1 min的数据取平均，分别得出两个位置IMU平均输出数据：

根据式(8)，两个位置可以得到6个六元一次方程组成的方程组，解此方程组，即可得到IMU偏置，结果见表1。

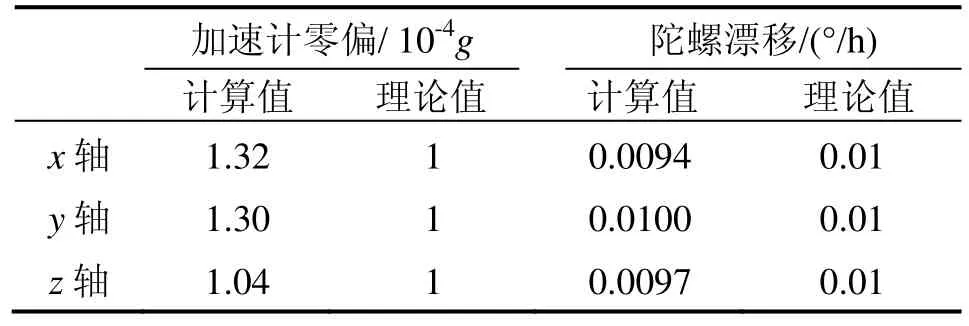
表1 IMU偏置Tab.1 Constant biases of IMU

通过表1可以看出，IMU偏置可以得到有效计算，但也存在误差，计算误差主要是由一阶近似误差与测量噪声引起。

需要指出的是，在某些特殊位置，比如两个位置的水平角同为零（即横滚角和俯仰角都为零），方程组的系数阵为奇异阵，无法求得IMU的偏置。因此要避免这种情况的发生，或者增加一个观测位置，即可求得IMU的偏置。

通过观察还可以发现，当载体处于某些特殊位置时，可以计算特定轴向的偏置。当载体近似水平时，由式(5)可以计算天向加速计零偏；当 IMU某轴接近地球自转轴的时候，由式(6)可以计算该轴向的陀螺漂移。

3 结 论

本文对最简多位置对准进行了研究，推导了 IMU偏置的解析表达式，提出了计算IMU偏置的解析法，指出解析法计算简单，不受先验信息的影响。通过解析法，一个位置可得到3个六元一次方程，两个位置即可得到6个六元一次方程组成的方程组，解此方程组，可计算求得IMU偏置，计算误差主要由一阶近似误差和测量噪声引起。某些特殊情况下，需要三个位置求解IMU偏置。某些特殊位置可以计算特定轴向的偏置。

（References）：

[1] Paul G S. Blazing gyros: The evolution of strapdown inertial navigation technology for aircraft[J]. Journal of Guidance, Control, and Dynamics, 2013, 36(3): 637-655.

[2] Liu X X, Xu X S, Wang L H, et al. A fast compass alignment method for SINS based on saved data and repeated navigation solution[J]. Measurement, 2013, 46(10): 3836-3846.

[3] Jiang Y F, Lin Y P. Error estimation of INS ground alignment through observability analysis[J]. IEEE Transactions on Aerospace and Electronic Systems, 1992, 28(1): 92-97.

[4] Cho S Y, Lee H K, Lee H K. Observability and estimation error analysis of the initial fine alignment filter for nonleveling strapdown inertial navigation system[J]. Journal of Dynamic Systems, Measurement and Control, 2012, 135(2): 44-45.

[5] Wang X L. Fast alignment and calibration algorithms for inertial navigation system[J]. Aerospace Science and Technology, 2009, 13(4-5): 204-209.

[6] Wu Y X, Zhang H L, Wu M P, et al. Observability of strapdown INS alignment: A global perspective[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(1): 78-102.

[7] Xiong J, Guo H, Yang Z H. A two-position SINS initial alignment method based on gyro information[J]. Advances in Space Research, 2014, 53(11): 1657-1663.

[8] 周广涛, 陈明辉, 刘星伯, 等. 新的两位置组合对准方法研究[J]. 传感器与微系统, 2008, 27(9): 17-20. Zhou G T, Chen M H, Liu X B, et al. Research on new two-position integrated alignment[J]. Transducer and Microsystem Technologies, 2008, 27(9): 17-20.

[9] Lee J G, Park C G, Park H W. Multiposition alignment of strapdown inertial navigation system[J]. IEEE Transactions on Aerospace and Electronic Systems, 1993, 29(4): 1323-1328.

[10] Chung D, Lee J G, Park C G, et al. Strapdown INS error model for multiposition alignment [J]. IEEE Transactions on Aerospace and Electronic Systems, 1996, 32(4): 1362-1366.

[11] 赵长山, 秦永元, 周琪. 参数辨识双位置对准改进算法[J]. 中国惯性技术学报, 2009, 17(6): 631-635. Zhao C S, Qin Y Y, Zhou Q. Modified two-position parameter identification alignment method[J]. Journal of Chinese Inertial Technology, 2009, 17(6): 631-635.

[12] Tan C M, Zhu X H, Wang Y, et al. Multi-position alignment with arbitrary rotation axis for SINS[J]. Journal of Chinese Inertial Technology, 2015, 23(3): 293-297.

[13] 孟卫锋, 袁爱红, 贾天龙, 等. 高精度惯性平台十六位置自标定方案[J]. 中国惯性技术学报, 2015, 23(2): 150-155. Meng W F, Yuan A H, Jia T L, et al. 16-position self-calibration of high-accuracy inertial platform[J]. Journal of Chinese Inertial Technology, 2015, 23(2): 150-155.

[14] 谭彩铭, 王宇, 苏岩, 等. 捷联惯导系统最简多位置解析对准[J]. 北京航空航天大学学报, 2015, 41 (9): 1645-1650. Tan C M, Wang Y, Su Y, et al. The simplest multi-position analytic alignment for SINS[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(9): 1645-1650.

Improved algorithm of the simplest multi-position analytic alignment for SINS

As a simple method for measuring IMU biases, the simplest multi-position analytic alignment reduces engineering complexity of traditional method and is free from the limitation of servo platform. However, the geometric method, which is used by the simplest multi-position analytic alignment, is complex for calculating and the accuracy of this method is affected by the prior information. To solve this problem, an analytic method is proposed and the analytic expressions of IMU biases are derived. The constant biases can be usually obtained through the information in two positions. Three positions are needed in particular cases. The constant bias of a certain axis can be well estimated when IMU stays in a particular attitude. The analytic method is easy to calculate and is unaffected by the prior information. Simulation results demonstrate that this method is effective and the calculation errors are mainly caused by the first-order approximation errors and the measurement noises.

strapdown inertial navigation system; multi-position alignment; analytic alignment; constant bias

P227.9

：A

2016-03-30；

：2016-04-12

国家自然科学基金（41274084，41406115）

丁磊香（1982—），男，博士研究生，从事组合导航研究。E-mail: dingleixaing@163.com

1005-6734(2016)03-0296-03

10.13695/j.cnki.12-1222/o3.2016.03.004

DING Lei-xiang1,2, XU Hou-ze1, WANG Yong1, CHAI Hua1, CAI Xiao-bo1,2

(1. State Key Laboratory of Geodesy and Earth’s Dynamics, Institute of Geodesy and Geophysics, Wuhan 430077, China; 2. University of Chinese Academy of Sciences, Beijing 100049, China)