基于北斗差分定位的炮载惯导外场标定
王志伟,秦俊奇,狄长春,石志勇,王风杰
(1. 军械工程学院,石家庄 050003;2. 陕西华阴63870部队,华阴 714200)
基于北斗差分定位的炮载惯导外场标定
王志伟1,秦俊奇1,狄长春1,石志勇1,王风杰2
(1. 军械工程学院,石家庄 050003;2. 陕西华阴63870部队,华阴 714200)
针对炮载惯导设备在外场标定过程中依赖固定基准点的问题,提出了一种基于卫星差分定位的误差标定新方法。该方法将北斗天线的安装误差、惯性器件的失准角以及安装误差等角度误差统一归为非对准误差。首先利用北斗测姿技术提供姿态基准,粗标出上述误差;精标阶段采用卫星差分技术来提供高精度位置信息,完成误差角的精确标定。多组标定结果与传统工厂标定方法结果相差均在0.3 mil以内,达到了较高的精度。该方法不仅回避了对固定基准点的依赖,而且避免了滤波带来的繁琐过程,即能保证长时导航的精度,又提高了标定的实时性。
北斗二代;差分定位;卫星测姿;捷联惯导;安装误差角
对于捷联惯导设备而言,惯性器件存在逐次启动零偏重复性误差、漂移误差等问题,在使用一段时间后零位误差会发生较大变化,同时安装误差也会发生变化,为确保捷联惯导设备的良好性能,需对其重新进行标定[1]。但是实验室标定需频繁拆卸捷联惯导设备,带来很大的经济负担和工程实用性问题[2-3]。因此捷联式惯导装备的外场自标定是亟需解决的问题。
现阶段,装备出厂前的标定是利用基准点和已知高精度外部信息来进行的。不足之处是,每次标定都需要以固定的基准点为参考,然而不是每个使用单位都有基准点,这就使得炮车出厂后在部队条件下无法进行外场自标定,更不可能在战场环境下对炮载惯导误差进行补偿。另外,大部分现役自行火炮所搭载的惯导系统没有公开的接口来采集惯导原始数据,只有火控计算机以50 Hz频率输出姿态和位置信息[4]。
文献[5]提出了九位置系统级标定方案,标定出了除陀螺标度因数外的15个主要参数,该方法需要精确地转位,不适合在战场条件下使用;Akcayir Y指出在利用转位标定误差时,角位置的个数取决于惯组误差模型中的未知参数的个数[6];文献[7]利用经纬仪进行了惯组和炮管之间安装误差的标定,并通过实验验证了所提方法的有效性。
但是以上各个方法中都需要获取惯导系统的陀螺和加速度计原始信号,势必要重复设计导航算法和修正程序,费时费力,最重要的是原始信号根本无法获取,无法实现[4]。另外,利用卡尔曼滤波方式与捷联惯导系统进行数据融合的方式存在如下几个问题[8-9]:首先,捷联惯导系统误差模型不准确,将导致卡尔曼滤波参数估计出现较大偏差;其次,标定场地限制,需要较为平直的道路,同时对基准点过分依赖,使得标定地点受到极大的限制;最后,里程计信息、卫星信息可能会出现野值,另外卫星信息获取存在较大的限制,卡尔曼滤波器的观测值的真实性与有效性不能保证。
考虑到光纤陀螺标度因数非常稳定,而且光纤陀螺捷联惯导系统外场自标定具有其自身的特点[10],本文不考虑器件误差,所以静基座初始对准或调平结束时的水平姿态误差是捷联惯导系统的主要误差,然后利用卫星测向技术提供定向基准,全方向多个角度进行短时间数据采集,粗标出系统误差。精标阶段采用卫星差分技术提供高精度位置信息,将北斗天线的安装误差、失准角以及惯性器件安装误差等统一归类为非对准误差,并完成对其的标定,从而保证捷联式惯导装备后期的长航时导航精度。
1 初始粗量测
1.1 卫星测姿原理
在粗标惯导系统的系统误差的过程中,需要建立一个相对精确地基准,为了满足外场条件,这里利用两个固联在载体上的北斗天线进行测向,提供姿态标定的基准。两个北斗天线构成二维基线向量,反映了载体的二维姿态(偏航和俯仰)。以载波相位测量值为观测对象,利用不同接收机、不同卫星、不同历元之间的载波相位差值,精确求解基线向量在东北天坐标系中的坐标关系,从而精确地确定载体的偏航角和俯仰角[11]。具体过程在这里不再赘述。
1.2 初始粗量测过程
在进行精标之前,首先要对粗大误差进行粗量测,以便提高精确标定的精度。在本文中,粗量测的对象是卫星测姿系统与惯导坐标系之间的角度差,也就是北斗测姿系统和惯性器件之间的安装误差。
从几何的角度来看,正交矩阵作用是将补偿后捷联式惯导三轴矢量相对于载体坐标系旋转一个固定的角度,此时相当于引入了一种两坐标系之间的初始误差角。坐标系之间的非对准示意图如图1所示。

图1 坐标系非对准示意图Fig.1 Schematic of non-aligned coordinate systems
图1中,坐标系的转动过程为:

b为载体坐标系,s为卫星测姿系统坐标系,设三次转动的变换矩阵分别为Cβ1、Cβ2、Cβ3,则坐标系的转换关系如下:
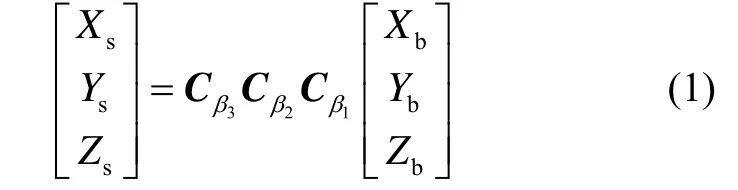
式中,

假设OXbYbZb表示载体坐标系,OXsYsZs表示补偿后捷联式惯导三轴矢量所确定的坐标系,β1、 β2、β3为初始误差角,假设卫星测姿输出为Hs,捷联式惯导三轴矢量为Hb,则两者的关系可表示为:
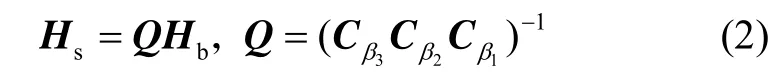
式中,
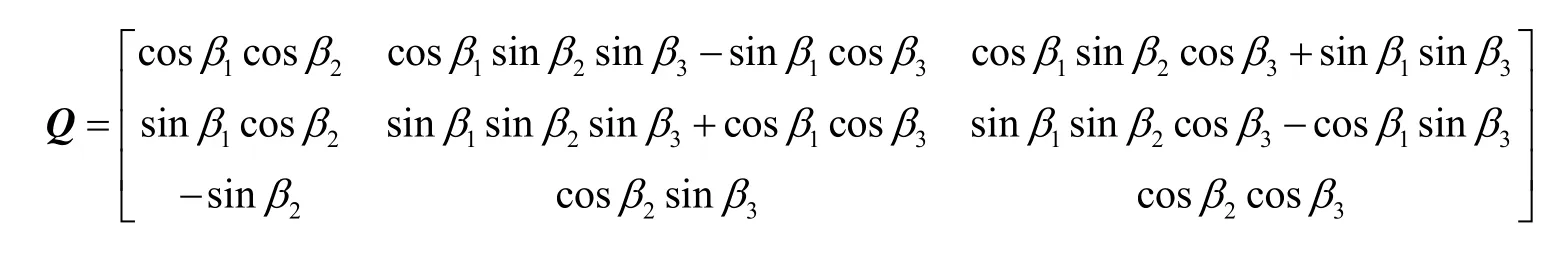
若能确定出β1、β2、β3,便可将补偿后捷联式惯导三轴矢量重新恢复到载体坐标系中。而由式(2)可知,可由卫星输出Hs和惯导输出Hb确定出正交矩阵Q,进而确定出β1、β2、β3。
2 精确标定
经过粗劣量测,粗大误差已被补偿,精确估计的目的就是为了消除微小误差,包括对准后遗留的非对准角,粗劣估计遗留的误差角,以及有惯性器件自身误差造成的量测偏差等。本节利用卫星差分定位出载体的真实位置,辅助完成上述精确估计过程。
2.1 卫星差分定位原理
实现卫星常规差分的基础是至少具备一台基准站接收机和一台移动站接收机。如图2所示,基准站与移动站同时进行单点定位,接收各自的定位数据,而基准站的位置坐标是经过长时间卫星解算得到的(认为是真实的)。当开始工作时,基准站接收到卫星的测量值后与真值进行数据解算,输出位置改正数。
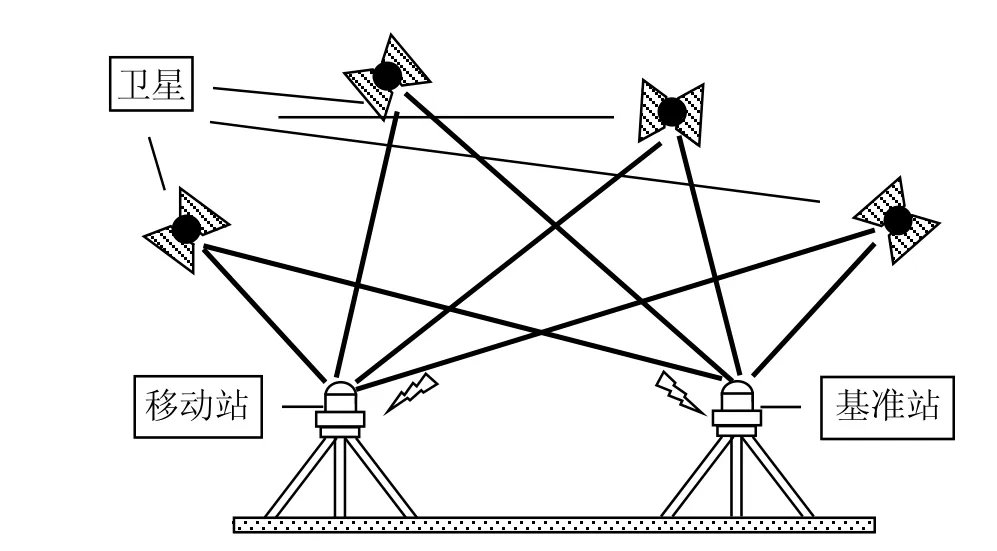
图2 GNSS差分原理Fig.2 Differential principle of GNSS
2.2 精确估计过程
文献[12]对航位推算产生的误差进行了分析,并推导了误差方程。下面提出对非对准误差角进行补偿的方法,将安装误差角归类到捷联式惯导的非对准误差角中,通过外部信息进行修正和补偿,来减小航位推算的误差,同时对陀螺的漂移进行大致的估计。
1)误差角补偿
设在ti-1时刻卫星测姿定向系统的速度输出在导航坐标系上的投影矢量形式为
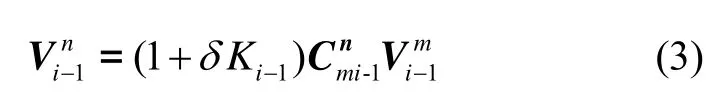
式中,δKi-1为卫星量测标度因数误差,由式(3)可得,在一小段时间Δt内航位推算实际公式:

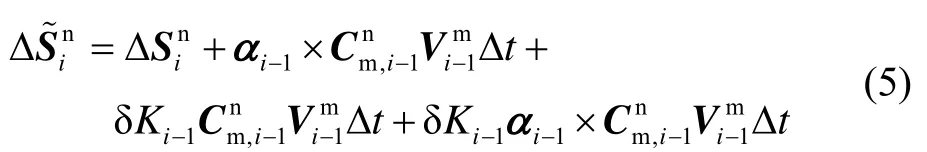
可得航位推算位移误差方程:

设
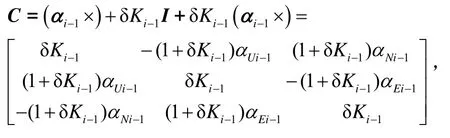
分析上式可得,当αi-1×、δKi-1不全为零时,矩阵C满秩,所以当位移误差 δΔS为零时,ΔS必为零,即东、北、天向速度矢量和为零,载体回到起始点。
假设标度因数δK和剩余非对准角矩阵α×不变,忽略高阶小量,则 ti时刻累计位移误差方程为
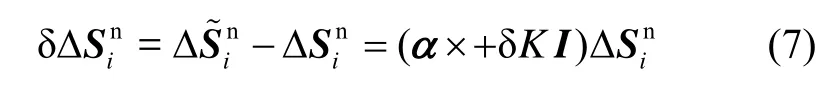
将其在OEN坐标系下投影,见图3,从式(7)可以看出,位移误差与行驶的方向无关,只与当前点各个方向上的位移有关。从而若已知载体实际位置坐标,则可由航位推算位置和实际位置得出剩余非对准角α。由于载体的航向误差为主要姿态误差[11],所以这里仅对 αU进行求解。由起始点与实际位置点间的矢量ΔS和起始点与航位推算点的矢量 Δ,利用简单几何关系,可求得初始误差角 αU。

图3 初始误差角计算原理图Fig.3 Calculation schematics of initial error angle

移项整理得:
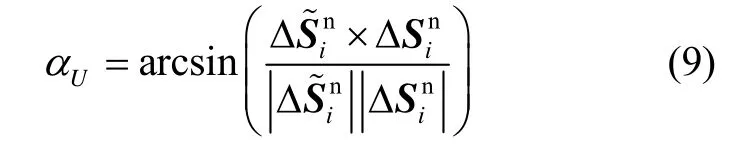
2)标度因数误差补偿
对于标度因数,从式(9)可以看出,方程满足叠加定理,故当姿态误差角矩阵×α为零时,得到标度因数补偿公式:

综上所述,理想的补偿方案就是,如果捷联惯导初始对准后误差较大,在粗略量测后,首先利用卫星差分定位技术测出当前精确坐标,行驶一段距离后,放慢车速,忽略惯性器件误差的影响,进行初始误差角的补偿,并对卫星测姿定向系统标度因数进行补偿。同时可以不断利用上述方法对系统的航向角及速度进行修正和补偿。
3 实验验证
3.1 静态试验
2015年9月17日在山西太原247厂进行了静态试验,目的是验证卫星测姿系统的精度。在做静态实验时,首先对炮载惯导进行对准。对准时从车载炮系统中可以读出当前坐标X:4196968,Y:799。对准结束后开始第1步~第5步数据采集。在前5步数据采集中,尽量保证身管的射角为0°。每步采集数据都需要调炮90°。实验时,前5步数据中身管的方向与高低如表1所示。
每一步采集数据15 min,当采集数据时间达到15 min后,停止对火控台输出数据的采集。改变身管的位置后,开始下一步,重新采集数据。身管旋转一周,分5步进行,所以需要5步进行采集数据。最后一步身管与车身相对位置回到起始时刻,采集一组数据。
将身管与车身的高度调为30°,重新进行对准,对准结束后开始重新标定,步骤与前5步相同。身管与车身之间角度为30°时,身管的方向与高低如表2所示。

表1 角度为0°时身管与车身的相对位置Tab.1 Relative position between barrel and body at 0° barrel angle
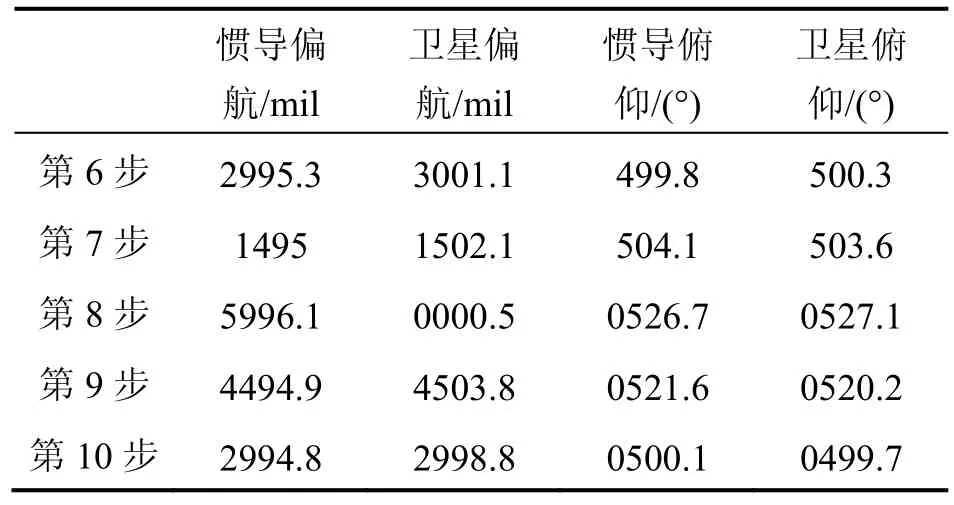
表2 角度为30°时身管与车身的相对位置Tab.2 Relative position between barrel and body at 30° barrel angle
由于篇幅限制,这里只选取一组静态数据(第二组)如图4~5所示。
静态实验结果中,从表1、表2的偏航数据中可看出,卫星测姿系统的输出始终比惯导输出大 3~7 mil,显而易见,这是由两个北斗天线安装的非同轴误差,以及卫星测姿系统量测误差造成的。该误差会导致姿态误差的产生,所产生的姿态误差会被当作剩余非对准角在精对准过程中进行补偿。为了确保不出现粗大误差,在下一步动态实验过程中安排了两次对准。

图4 偏航角实时数据Fig.4 Real-time data of yaw angle
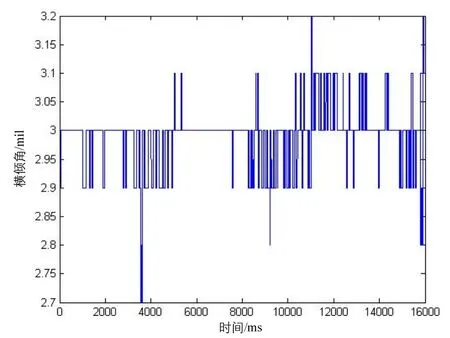
图5 俯仰角实时数据Fig.5 Real-time data of pitch angle
3.2 动态试验
工厂在对将要出厂的炮车所搭载的惯导系统的系统误差、定位误差、方向漂移以及寻北误差进行标定时,都需要固定的基准点,按照特定的程序行驶到每个基准点,通过已知高精度信息来进行不同的误差标定。而通过固定标准点检测方法对基准点的依赖程度太高,不具有普适性。这里采用高精度差分卫星(基准站+移动站,定位精度≤1cm,输出数据为北京54大地直角坐标系格式)进行,检测时差分卫星基准站设立在某一固定标准点(由基准站长时定位得到),移动站设置在尽可能靠近惯导的位置随火炮行驶,每行驶超过 5 km 读取一次惯导导航值、移动卫星导航值以及卫星测姿系统数据,移动站和基准站最大直线距离不超过 80 km。利用补偿算法得出修正量,通过电台反馈到车载惯导。
2015年12月9日在山西太原榆次方向对本系统进行了试用,并与247厂外场标定方法进行比对,动态跑车实验(北斗天线三个、基准站一套、移动站一套、连接线一套)的试验过程如下:
① 在炮车行驶至第一个基准点时停车进行对准,将基准站天线放置于地势较高的方位,流动站跟随炮车,流动站主天线固定在炮塔顶端的中心位置,并将电台置于其一侧,另外将从天线固定于平衡机外壳上方,使主、从天线尽量位于同一中轴线上。;
② 为了保证惯导精度,在炮车行驶至第二个基准点时停车对准;
③ 当行驶至第三个基准点时按照本文提出的方法进行初始误差角的标定;
④ 重复③中的过程6次。
最后将本方案所得数据与工厂标定方法所得数据进行对比。
上述过程是工厂采用的跑车方案,其中的基准点是工厂方面通过测地得出的精确信息,与本文标定方案无关,本文所提标定过程与工厂标定过程同时在一门炮内进行。
图6~图9为本系统在实际标定过程中。
工厂标定的目的是修正惯导参数,消除较大的误差,提高导航精度,使其达到出厂的标准。本文将所提方案与工厂标定的结果进行全程对比,如表3所示。
表9中的9个点为工厂预先设定好的标准点,所用坐标系为北斗二代所用的北京54坐标系,炮车行驶至前两个点时需要进行初始对准,所以在没有记录第一个点的导航结果。
表 9中倒数第二列为用工厂的方法得出的剩余非对准角,最后一列为用本系统标定出的初始误差角。从标定结果可看出,第二个点的剩余非对准角较大,但是经过两次对准修正后,接下来的七个点处的剩余非对准角均在2.8 mil以内,说明现阶段工厂所采用的标定方法已经达到了很高的精度。
而本文所提方案的标定结果较之工厂标定结果,在点7处相差最大,为0.3 mil,其余均在0.3 mil以内。表明北斗卫星差分定位精度完全满足对车载惯导进行标定的要求,也说明该方法可以很好地将粗标定过程中,由北斗天线非同轴误差以及北斗测姿系统量测误差造成的剩余误差补偿掉,其精度完全满足部队作战的需求。

图6 捷联式惯导装备外场标定系统基准站Fig.6 Outfield calibration system reference station for SINS equipment

图7 基准站天线Fig.7 Antenna of the base station

图8 捷联式惯导装备外场标定系统移动站Fig.8 SINS equipment field calibration system for mobile station

表3 实车实验数据Tab.3 Test data of real vehicle

图9 移动站天线Fig.9 Antenna of the mobile station
4 结 论
在本文中,将惯性器件安装误差角、北斗天线非同轴安装误差以及对准后遗留的失准角归类到捷联式惯导的非对准角中。首先利用卫星测姿系统为惯导系统提供姿态基准,完成了误差角的粗标定;然后利用卫星差分定位原理为精标定过程提供位置基准。在标定过程中,基准站通过电台将定位误差反馈给移动站,最后通过移动站计算出载体的误差角。
本文所提方法和系统在标定过程中不需要已知的基准点,并且在精量测阶段不需要滤波,避免了繁琐的估计过程。所得标定结果与工厂高精度标定方法所得结果相差不大,完全可以满足部队条件下的标定任务。
(References):
[1] Han K J, Sung C K, Yu M J. Improved calibration method for SDINS considering body-frame drift[J]. International Journal of Control, Automation, and Systems, 2011, 9(3): 497-505.
[2] Gao J, Petovello M G, Cannon M E. Development of Precise GPS/NS / Wheel Speed Sensor/Yaw Rate Sensor Integrated Vehicular Positioning System[C]// National Technical Meeting of the Institute of Navigation. Monterey, Canada, 2006: 780-792.
[3] Obradovis D, Lenz H, Schupfner M. Fusion of sensor data in siemens car navigation system[J]. IEEE Transactions on Vehicular Technology, 2007, 56(1): 43-50.
[4] GJB 8254-2014. 自行火炮捷联式惯导系统通用规范[S]. 北京: 兵器工业集团, 2011. GJB 8254-2014. General specification for self-propelled strapdown inertial navigation system[S]. Beijing: Ordnance Industry Group, 2011.
[5] 贾继超, 秦永元, 张波, 等. 激光陀螺捷联惯导系统外场快速标定新方法[J]. 中国惯性技术学报, 2014, 22(1): 23-25. Jia Ji-chao, Qin Yong-yuan, Zhang Bo, et al. New fast systematic calibration method for RLG-SINS[J]. Journal of Chinese Inertial Technology, 2014, 22(1): 23-25.
[6] Akcayir Y, Ozkazanc Y. Gyroscope drift estimation analysis inland navigation systems[C]//Proceedings of 2003 IEEE Conference on Control Applications. 2003: 1488-1491.
[7] 严恭敏, 严卫生, 徐德民, 等. 捷联惯组与炮管之间安装误差角的标定方法[J]. 火力与指挥控制, 2009, 34(7): 53-56. Yan Gong-min, Yan Wei-sheng, Xu De-min, et al. Misalignment angle calibration between simu and gun barrel [J]. Fire Control &Command Control, 2009, 34(7): 53-56.
[8] Dmitriyev S P. Nonlinear filtering methods application in INS alignment[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 33(1): 260-271.
[9] Choukround D, Bar-Itzhack I Y, Oshman Y. Novel quaternion Kalman filter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(1): 35-42.
[10] 江奇渊, 汤建勋, 袁保伦, 等. 激光陀螺捷联惯导尺寸效应误差分析与补偿[J]. 红外与激光工程, 2015, 44(4): 1110-1114. Jiang Qi-yuan, Tang Jian-xun, Yuan Bao-lun, et al. Analysis and compensation for size effect error of laser gyro strapdown inertial navigation system[J]. Infrared and Laser Engin eering, 2015, 44(4): 1110- 1114.
[11] Saab S. Automatic alignment and calibration of an inertial navigation system[C]//IEEE Position Location and Navigation Symposium. 2014: 845-852.
[12] 严恭敏. 车载自主定位定向系统研究[D]. 西安: 西北工业大学, 2006. Yan Gong-min. The study of autonomous position and azimuth determining system(APADS)[D]. Xi’an: Northwestern Polytechnical University, 2006.
Inertial navigation system’s field calibration based on Beidou-II differential positioning
WANG Zhi-wei1, QIN Jun-qi1, DI Chang-chun1, SHI Zhi-yong1, WANG Feng-jie2
(1. Ordnance engineering college, Shijiazhuang 050003, China; 2. Unit 63870 of PLA, Huayin 714200, China)
In view that the calibration of inertial navigation system under field conditions needs fixed reference points, a novel calibration method is proposed based on satellite positioning differential. In this method, the antenna installation error, angular misalignment and installation errors and other inertial devices are classified as a unified installation error angle. Based on the dead reckoning error compensation, a positioning reference is provided based on Beidou attitude measurement technology to coarsely calibrate the system error. In fine calibration stage, a high-precision location information is provided by satellite differential technology to complete a calibration error angle. Multiple sets of calibration results show that their differences from traditional factory calibration results are within 0.3 mil, which achieve higher accuracy. This approach not only avoids reliance on the fixed reference point, but also prevents tedious processes in filtering the result, eliminating the known external information, which guarantee the accuracy of long navigation and improve the real-time calibration.
Beidou-II satellite navigation; differential; satellite attitude determination; strapdown inertial navigation system; misalignment angles
U666.1
:A
2016-02-19;
:2016-05-27
国防预研基金(9140A09040112JB34111)
王志伟(1990—),男,博士研究生,研究方向为惯性导航。E-mail: wzw505869351@126.com
联 系 人:秦俊奇(1961—),教授,博士生导师,研究方向为故障诊断技术、组合导航技术。E-mail: Qjq1961@yeah.net
1005-6734(2016)03-0314-06
10.13695/j.cnki.12-1222/o3.2016.03.007

