基于四元数法进行发射车不调平瞄准控制
刘显勤,吴林瑞,赵慧莉
(北京航天发射技术研究所,北京,100076)
基于四元数法进行发射车不调平瞄准控制
刘显勤,吴林瑞,赵慧莉
(北京航天发射技术研究所,北京,100076)
利用四元数法推导发射车不调平进行瞄准控制的起竖角和回转角,给出起竖角和回转角理论确定值计算式的推导过程,并与现有的修正方法进行了比较。研究结果表明,四元素法可以比较简单地实现不调平进行瞄准控制起竖角和回转角的解算,用于发射车不调平的瞄准控制。
四元数;不调平;瞄准
0 引 言
倾斜式发射车可以为战术导弹、火箭弹等提供初始射角和射向(大地坐标系)。进行瞄准时,如果测量值不是绝对角度(如采用轴角编码器测量起竖、回转的相对角度),当射向瞄准的回转轴与水平面不垂直时,会使起竖和回转运动存在耦合,导致相对测量值的起竖角与大地坐标系的俯仰角、相对测量值的回转角与大地坐标系的方向角之间存在强非线性关系,这给瞄准特别是高精度瞄准带来了不可忽视的误差。通常的方法是进行发射车调平,使回转平台的水平度在可接受的范围内,保证瞄准精度在误差范围内。当发射车不平度较大时,要达到较高的调平精度,不但需要较长的时间,而且也对结构受力不利。由于采用调平的方法减小瞄准偏差存在上述问题,因此寻求发射车不进行调平而进行起竖回转的方法变得相当重要。
文献[1]、文献[2]采用欧拉坐标变换进行推导,计算效率问题在推导坐标转换时进行了简化处理。本文在只考虑不调平对瞄准的影响的基础上,采用四元数法对不调平发射车进行起竖回转解耦,得到了起竖角和回转角的确定计算式。
1 基本条件说明
设R为导弹瞄准线的单位向量,用来确定瞄准的俯仰角和方向角;设Rm为目标俯仰角和方向角的导弹瞄准线的单位向量。
1.1 定义坐标系
a)回转平台坐标系o-x1y1z1:o为回转机构中心,平面ox1y1为回转平台平面,y1轴由车头方向指向车尾方向,与导弹瞄准线的初始向量在平面ox1y1内的投影重合,z1轴垂直于平面ox1y1竖直向上,右手系确定x1轴;
b)地理坐标系o-xyz:o为回转机构中心,平面oxy为水平平面,y轴由车头方向指向车尾方向,与导弹瞄准线的初始向量在平面oxy内的投影重合,是方向角变化量的基准轴,z轴垂直于水平面竖直向上,右手系确定x轴。
1.2 角度变量说明
a)目标高低角ψ:ψ为与水平面的夹角,0~65°之间为正;
b)目标方向角γ:导弹瞄准线在oxy面内的投影与-y轴的夹角,-30~30°,从+z轴看,逆时针为正;
c)x1轴、y1轴与水平面的夹角α、β:从+x1轴与+y1轴的正向看,逆时针为正;由安装于回转平面的水平测量仪测量得到;
d)坐标转换角δ、φ:由o-xyz先绕x轴转动角δ,得到o-x′y′z′;再绕y′轴转动角φ,得到o-x1y1z1;从+x轴、+y′轴看,逆时针为正,计算得到;
e)起竖角σ,回转角θ:进行起竖回转的角度,从+z轴、+x轴看,逆时针为正,由轴角编码器测量得到。
2 四元数在刚体转动中的应用
本文的坐标转化采用四元数方法进行,本质上与采用欧拉角的坐标变换一致。
所谓四元数是由1个实数单位“1”和3个虚数单位“i”、“j”、“k”组成并具有下列形式的数[3~5]:

四元数的加法、减法与复数的一致;乘法“⊗”满足结合律,但不满足交换律;单位1,i,j,k的乘法规则如下:

刚体转动的四元数表示:将虚数单位i,j,k与空间坐标系坐标轴的单位向量i,j,k对应起来,刚体向量F绕某轴n转动ϕ角,n为转动轴的单位向量。
绕n轴转动ϕ角的四元数表示为

刚体向量F绕n轴转动ϕ角后,得到F′:

3 推导解耦的起竖角和回转角
只考虑不调平对瞄准的影响,作如下假设:
a)水平仪测量平面与回转平面重合,测量轴为1x轴和1y轴;
b)起竖轴q平行于回转平面,且垂直于导弹瞄准线,即与1x轴平行。
不调平进行标准控制的起竖角和回转角的推导流程如图1所示。按照图1所示推导流程进行不调平起竖角、回转角的推导。地理坐标系o-xyz的坐标轴x,y,z的单位向量分别为i,j,k。

图1 推导流程
3.1 导弹瞄准线的目标单位向量
根据目标高低角ψ 和方向角γ,可得到Rm:
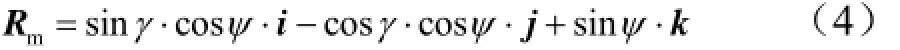
3.2 o-x1y1z1坐标轴单位向量及坐标转动角
坐标转动方式为:由o-xyz先绕x轴转动角δ,得到o-x′y′z′;再绕y′轴转动角φ,得到坐标系o-x1y1z1;从转动轴的正向看,逆时针转动为正。由转动方式可知,x轴与x′轴重合,y′轴与y1轴重合。
用四元数计算x1轴、y1轴和z1轴的单位向量,坐标转动角δ 和角φ,步骤如下:
a)计算y1轴的单位向量oy1。
由坐标转换方式可知,oy1由oy绕x轴转动角δ
得
到,oy1与y′轴重合,ox = i,oy = j。
绕x轴转动角δ 的四元数表示为

oy绕x轴转动角δ 得到oy1,表示为

oy1与水平平面oxy的夹角,即为水平仪测量的角度β,可得到:δ = β。
b)计算x1轴的单位向量ox1。
由坐标转换方式可知,ox1是由ox绕y′轴转动角φ得到,其中y′轴的单位向量oy′ = oy1。
绕y′轴转动角φ 的四元数表示为
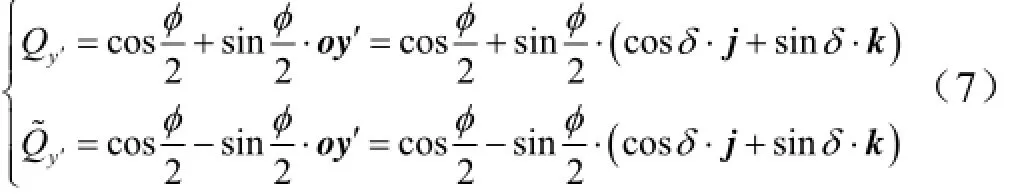
ox绕y′轴转动φ 角得到ox1,表示为

ox1与水平平面oxy的夹角,即为水平仪测量的角度α,可得到:
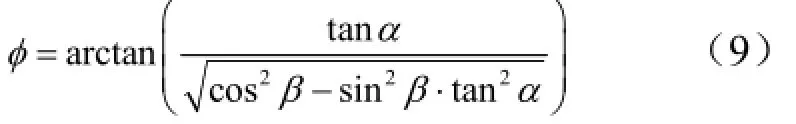
c)计算z1轴的单位向量oz1。
由坐标转换方式可知,oz1由oz绕x轴转动角δ,再绕y′轴转动角φ 得到,其中ox = i,oz = k,y′轴的单位向量oy′ = oy1。
oz先绕x轴转动角δ,得到oz′:

oz′再绕y′轴转动角φ,得到oz1:

综合以上计算得到:
a)坐标转换角度:

b)x1轴、y1轴和z1轴的单位向量坐标:

3.3 计算目标起竖和目标回转角度
根据式(4)、式(13)、式(14)可求得目标单位向量与回转平台平面的夹角,即为目标起竖角σm;目标单位向量在回转平台平面内的投影与1y-轴的夹角,即为目标回转角θm。
a)计算目标起竖角σm。
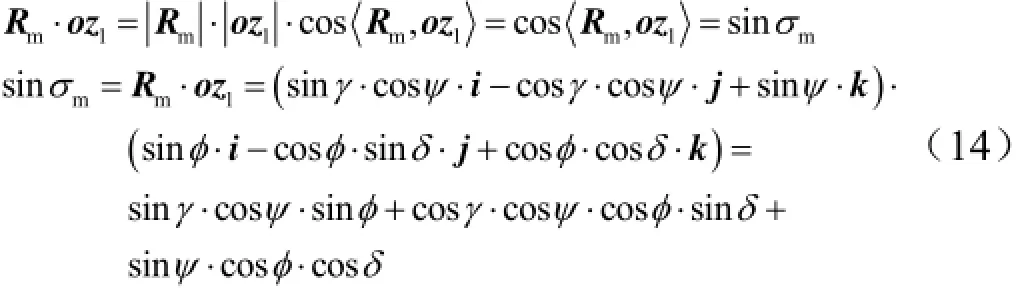
得到:
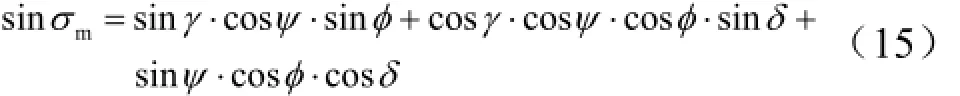
b)计算目标回转角θ。
得到:

综合以上,可得到目标起竖角σm和目标回转角θm:

其中,求得的θm,从+z轴看,逆时针回转为正;ψγ、由初始瞄准给出,δφ、由下式得到:
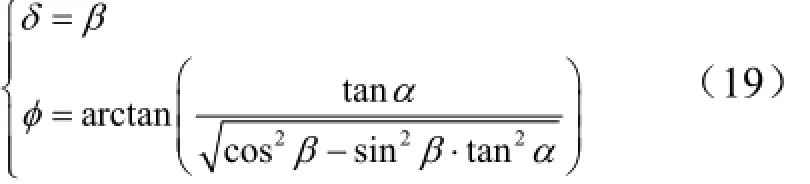
式中 α 和β 由水平仪测量得到。
实际进行起竖回转的过程中,由于重心的变化会影响回转平台的不平度,即水平仪的输出会有变化。由式(19)、式(20)可知,目标起竖角σm和目标回转角θm可以根据水平仪测量角α 和β 实时更新。
4 误差分析
受实际工装的影响,按照第3节中推导的起竖角、回转角,最终得到的俯仰角、方向角与目标之间存在一定的误差。当工装精度较差时,可能导致最终的俯仰角、方向角不能达到精度要求,因此对工装有较高的精度要求。
产生误差的原因有:
a)水平仪测量误差。由第3节中的推导可知,要求水平测量x1轴、y1轴与水平面的夹角,当测量存在误差时会对最终的俯仰角和方向角造成误差。为了便于分析,假设测量y1轴与水平面夹角存在误差Δ,测量x1轴与水平面的夹角不存在误差,那么,当方向角为零时,造成俯仰角的误差最大为Δ。
b)起竖轴的误差。当起竖轴不垂直于瞄准线或回转轴时,控制起竖角度为σm角,实际起竖角会小于σm。
假设起竖轴与x1轴存在夹角Δ=30′,起竖角σm= 50°时,实际起竖的角度σs≈49°59′53″,误差约为7″;当Δ<10′时,控制起竖角σm= 50°时,实际起竖的角度误差小于1″。
c)回转轴的误差。受安装影响,实际测量轴与目标轴之间存在1个小的夹角,这样实际转动的角度会比测量值大。
假设实际测量的回转轴与目标回转轴之间存在小夹角Δ = 30′,控制回转角θm= 30°时,实际回转角θs≈30°0′31″;当Δ<5′,回转角θm= 30°时,实际回转的角度误差小于1″。
5 与现有方法比较
文献[2]通过实时计算方向角与目标之间的误差来判断回转到位,而俯仰角采用石英加速度计直接测量。在起竖回转过程中存在一定缺点:如果起竖回转不能同时到位,就可能需要反复的调节;如当回转到位停止时,起竖还未到位,起竖会继续进行,由于回转平台不水平带来的起竖回转耦合,导致起竖过程影响方向角,因此需要再次进行回转调节;同理,回转也会影响俯仰角。
本文给出的是解耦后的起竖角与回转角,回转先到位(达到回转角)时,对应的方向角其实还未达到目标值;当起竖到位(达到起竖角)时,通过起竖与回转的耦合,方向角和俯仰角达到目标值。起竖先到位的情况也是如此。如果直接测量俯仰角(如采用石英加速度计),那么应当使回转先到位,俯仰角达到目标值时,方向角也就达到目标值了。
6 结束语
本文采用四元数法进行不调平瞄准,根据俯仰角和方向角的目标值,水平仪测量的回转平台的不平度,推导得到解耦后的起竖角和回转角,分析了工装精度对实际系统起竖回转的影响,并与现有方法进行了比较。
在加工和安装精度满足要求的情况下,本文提供的解算式,可直接用于倾斜式发射车不调平进行起竖回转控制的起竖角度和回转角的解算,不需再进行修正。
[1] 张胜三. 发射车不调平而进行瞄准角修正[J]. 导弹与航天运载技术, 2001(1): 38-42.
[2] 张胜三. 发射车不调平进行瞄准角修正的新方法[J]. 导弹与航天运载技术, 2007(4): 26-28.
[3] 许方官. 四元数物理学[M]. 北京: 北京大学出版社, 2012.
[4] 肖尚彬. 四元数方法及其应用[J]. 力学进展, 1993,23(2): 249-260.
[5] 赵双明, 郭秋燕, 罗研, 等. 基于四元数的三维空间相似变换解算[J].武汉大学学报: 信息科学版, 2009,34(10): 1214-1217.
Non-adjusting Level Aiming Control of Launcher Based on Quaternion Method
Liu Xian-qin, Wu Lin-rui, Zhao Hui-li
(Beijing Institute of Space Launch Technology, Beijing, 100076)
This paper introduces the derivation of erection angle and rotation angle of non-adjusting level aiming control of launcher based on the quaternion method. The derivation process of theoretical value calculation method of erection angle and rotation angle is given and compared with current correction method. The results show that, the quaternion method can be used to calculate erection angle and rotation angle of non-adjusting level aiming control, used for vertical and rotary control of launcher.
Quaternion; Non-adjusting level; Aiming
V55
A
1004-7182(2016)04-0044-04
10.7654/j.issn.1004-7182.20160411
2015-06-20;
2016-07-08
刘显勤(1985-),男,工程师,主要从事计算机控制方面研究

