助推-滑翔式导弹总体参数设计方法初探

蒋明明，袁庆航，赵长见，卜奎晨

（中国运载火箭技术研究院，北京，100076）

助推-滑翔式导弹总体参数设计方法初探

蒋明明，袁庆航，赵长见，卜奎晨

（中国运载火箭技术研究院，北京，100076）

以两级固体推进剂火箭发动机助推、弹头直接入轨，而后全程在大气层内滑翔飞行的助推-滑翔式导弹为研究对象，对导弹总体参数设计进行研究，给出一种适用于助推-滑翔式导弹的总体参数设计方法。根据助推-滑翔式导弹的弹道特点，通过分段分析弹道特性，推导出导弹总体参数与关机点理想速度间的关系式。通过仿真分析，建立滑翔起点参数与关机点参数间的关系模型；考虑平衡滑翔条件，得到滑翔射程公式。基于以上公式和模型，给出助推-滑翔式导弹射程与关机点参数之间的解析关系，初步建立了助推-滑翔式导弹总体参数的设计方法。

助推-滑翔式导弹；武器装备；总体参数设计

0 引 言

助推-滑翔式导弹是一种利用火箭助推，弹头在大气层内靠气动升力进行滑翔飞行的导弹武器。助推-滑翔式导弹结合了弹道导弹与巡航导弹的优点，可以实现大气层内高超声速飞行，实现远距离精确打击，具有强机动能力和突防能力，是目前世界主要军事大国导弹武器研究的主要方向。助推-滑翔式弹道的概念早在1933年就已经被提出，但由于科学技术发展水平的限制，基于这种弹道的高超声速滑翔飞行器一直处于验证阶段。近年来，以美国和俄罗斯为代表的主要军事大国正加紧验证助推-滑翔式飞行器的关键技术，并列入武器装备研究计划。

导弹总体参数的设计是导弹设计的基础，在方案论证阶段快速获得总体参数将有助于提高总体设计效率、缩短设计周期。文献[1]推导出了弹道式飞行器的航程公式；文献[2]推导出了单级弹道式飞行器、高超声速助推-滑翔式飞行器及高超声速助推-巡航飞行器的起飞质量与射程、推进剂比冲和载荷之间的解析关系；文献[3]通过引入射程经验公式并进行近似质量分析，将求解固体弹道导弹最优级间比转化为求解各子级推进剂质量比之间的关系，以最小起飞质量为优化目标，求得了n级导弹各级最佳推进剂质量比；文献[4]以导弹起飞质量最小为目标，对导弹质量进行近似分析，并忽略速度的阻力损失以及喷管出口压力损失，将求解n级液体弹道导弹最优总体设计参数转化为求解各级最优推进剂质量比和推重比，获得了可行的理论解法。

目前，助推-滑翔式导弹的总体参数设计尚未有系统的理论方法。本文根据助推-滑翔式导弹的弹道特点，对其弹道进行分段研究，得到导弹射程与关机点参数之间的解析关系，初步建立了助推-滑翔式导弹总体参数的设计方法，并通过设计实例验证此方法的可行性，为此类型导弹的总体参数设计提供了参考。

1 助推-滑翔式导弹总体参数设计方法

根据助推-滑翔式导弹的弹道特点，将其弹道分为助推段、无动力下压段、拉起段、滑翔段及下压攻击段，如图1所示。

在助推-滑翔式导弹的弹道中，滑翔段射程占导弹射程的绝大部分，助推段及下压攻击段射程占导弹射程比例较小，解析分析时可以忽略这2段对导弹全射程的影响。

1.1 导弹总体参数与关机点理想速度的解析关系

虽然助推段射程对于导弹全射程的影响很小，但其弹道特性直接决定了关机点参数，对导弹的射程及飞行控制等均有较大影响。因此，本节以两级固体导弹为例，研究导弹起飞质量等总体设计参数与关机点理想速度间的关系，为建立助推-滑翔式导弹总体参数设计方法打下基础。

引入发动机质量比σ1和σ2，导弹各级起飞质量可表示为

式中 Myx为有效载荷即弹头质量；M01和M02分别为导弹一、二级起飞质量；Mp1和Mp2分别为导弹一、二级推进剂质量；Mj1和Mj2分别为导弹一、二子级结构质量。

根据齐奥尔科夫斯基公式，两级导弹二级发动机关机时刻的理想速度Vk1为

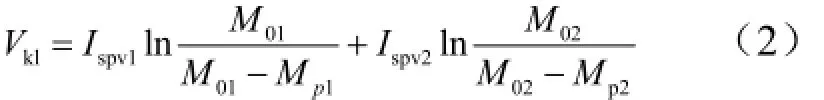
式中 Ispv1和Ispv2分别为导弹一、二级真空比冲。

引入有效推进剂质量比µki= Mpi/M0i，则有：

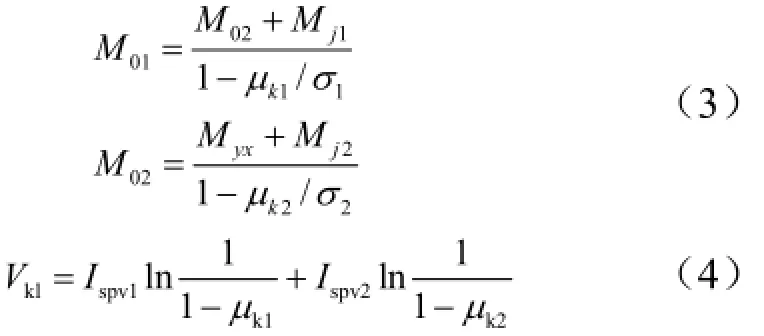
这是一个求函数条件极值的问题：Vk1给定的情况下，求M01为最小时的参数µk1和µk2。即为求下述拉格朗日函数无条件极值的问题：

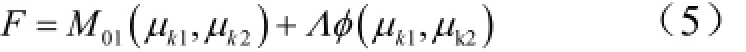
式中 Λ为待定拉格朗日乘子；φ 为约束条件：

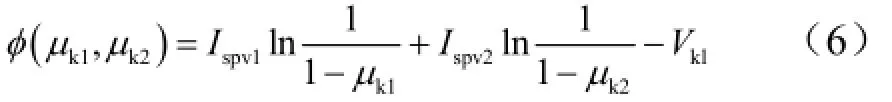
令Myx+Mj2= a，Mj1= b，Ispv2/Ispv1= c，经计算得：

在得到Vk1之后，可由式（7）求得二级有效推进剂质量比µk2，再将µk2带入式（8），即可求得一级有效推进剂质量比µk1。之后，即可计算Mp1和Mp2等参数，从而确定出导弹最优起飞质量。

通过计算验证公式推导的正确性计算条件如下：

a）Vk1= 4000 m/s，有效载荷（即弹头）质量为1600 kg；

b）Ispv1= 2600 (N·s)/kg，Ispv2= 2800 (N·s)/kg；

c）Mj1= 500 kg，Mj2= 200 kg。

导弹起飞质量与二级有效推进剂质量比、发动机质量比的关系曲线如图2所示。

图2 导弹起飞质量随有效推进剂质量比变化曲线

从图2中可以看出，对应不同发动机质量比，均有一个最优二级有效推进剂质量比使得导弹起飞质量最小，且其值与理论值相同，证明了导弹总体参数设计方法的正确性。

1.2 滑翔起点参数与关机点参数的关系

滑翔起点参数包括滑翔起点的速度和射程（即无动力下压段及拉起段射程之和），下面分别求解这2个参数与关机点速度Vk和关机点当地弹道倾角θk之间的关系。

通过仿真分析，滑翔起点速度值V0与关机点参数近似满足以下关系：

式中 a2和b2为拟合为kθ的多项式函数。

通过对仿真结果进行拟合，无动力下压段及拉起段的射程之和L1与关机点参数间近似满足以下关系：

式中 a1，b1，c可以拟合为Vk的多项式函数；Lke为以关机点参数为起点计算出的真空状态下的抛物线射程，计算公式[5]如下：

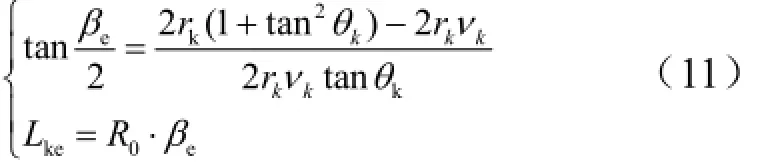
式中 βe为射程角；rk为关机点地心距；νk为关机点能量参数，；µ 为地球引力系数。

1.3 滑翔段射程公式

在进行滑翔段射程分析时，为了简化问题，对导弹滑翔运动模型作如下假设：

a）不考虑地球旋转，即ωe= 0；

b）地球为一均质圆球，即引力加速度与地心距平方成正比，g = fM/r2；

c）导弹仅在平面内运动，无滚转和侧滑。导弹滑翔段的运动方程为

式中 V，θ，h，φ 分别为导弹速度、当地弹道倾角、飞行高度及射程角；R0，ρ，S，m分别为球形地球半径、大气密度、导弹参考面积和质量；CL和CD分别为导弹的升力系数和阻力系数。

本文中，滑翔段采用平衡滑翔飞行，平衡滑翔指飞行器在大气层内无动力飞行时，沿航迹每一点处飞行器所受的升力、重力和离心力平衡，即0θ=˙的状态。对式（13）进行整理可得平衡滑翔状态受力关系为

高超声速飞行器滑翔距离一般在上千公里，而滑翔段高程变化一般小于50 km，因此当地弹道倾角和径向速度都很小，可以认为θ = 0，代入式（16）中可得：

由式（15）除以式（12），并结合平衡滑翔条件，可得平衡滑翔条件下射程角对滑翔速度的偏导数：

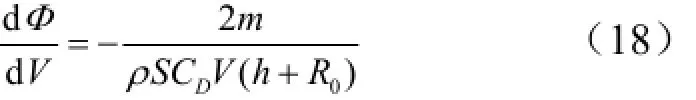
将式（12）代入式（13），并令K = CL/CD，整理可得：

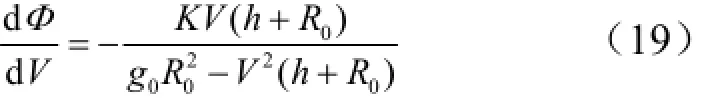
假设平衡滑翔过程中，升阻比K和高度h近似不变，设V0和h0分别为滑翔起始点的速度和高度，对式（19）进行积分，可得平衡滑翔射程角φ 与速度V的关系式：

相应的平衡滑翔射程为

由式（21）建立滑翔距离与升阻比、滑翔高度及滑翔速度的关系。其中，滑翔高度及升阻比均近似为常值，滑翔结束点速度可根据落地点速度约束选定，即平衡滑翔射程仅与滑翔起点速度值有关。

1.4 导弹射程与关机点参数之间的关系

将式（10）和式（21）相加，即可得到助推-滑翔式导弹全射程公式：

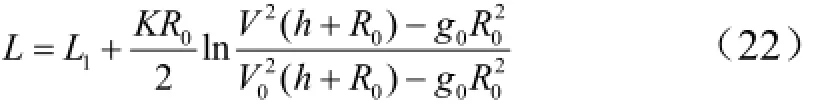
将式（9）及式（10）代入式（22），即建立了助推-滑翔式导弹射程与关机点速度Vk和关机点当地弹道倾角θk间的关系。

1.5 导弹总体参数与射程指标之间的关系

给定射程指标L及式（22）中的各常量后，即可求得助推-滑翔式导弹的关机点参数。之后，即可根据导弹总体参数与关机点理想速度间的解析关系，通过关机点参数求得助推-滑翔式导弹的起飞规模等总体设计参数。

2 仿真算例

技术指标要求：射程1300 km，弹头质量1600 kg。

一般，助推-滑翔式导弹关机点处当地弹道倾角θk较小，可取θk= 7°，滑翔升阻比K = 2.5，滑翔高度h = 40 km，滑翔结束点速度V = 1000 m/s；导弹一、二子级结构质量分别为500 kg和200 kg；一、二级发动机质量比σ1= σ2= 0.9；一、二级发动机真空比冲分别为Ispv1= 2600 (N·s)/kg，Ispv2= 2800 (N·s)/kg。

根据工程经验，经大量仿真计算，将a2和b2拟合为θk的五次多项式，a1，b1，c拟合为Vk的三次多项式函数，所得拟合结果较为理想。

由式（10），得到导弹关机点速度：Vk= 3017 m/s。

考虑到实际飞行中存在的速度损失，同时为简化问题，本文中取速度损失ΔVk= 0.25Vk，则理想速度：Vk1= Vk+ΔVk= 1.25Vk= 3771 m/s。

根据助推-滑翔式导弹总体参数设计方法，计算得到助推-滑翔式导弹总体参数为µk1= 0.32；µk2= 0.63；M01= 10 017 kg；M02= 5 964 kg。

为验证助推-滑翔式导弹总体参数设计方法的可行性，基于上述总体参数进行助推-滑翔式弹道的数学仿真验证。取一级真空推力P1= 280 kN，二级真空推力P2= 200 kN，并进行弹道仿真，仿真结果如图3所示。

仿真所得导弹落速为560 m/s，当地弹道倾角为-80°，导弹射程为1250 km，与设计指标间的误差为3.8%，由此可见，本文得到的助推-滑翔式导弹总体参数设计方法可以用于方案论证初期的导弹总体参数选择。

Preliminary Investigation of Parameter Design Method for Boost-Glide Missile

Jiang Ming-ming, Yuan Qing-hang, Zhao Chang-jian, Bu Kui-chen
(China Academy of Launch Vehicle Technology, Beijing, 100076)

Based on two class solid propellant missile whose warhead orbits directly and then glides in the aerosphere all along, missile parameter design is studied, and a parameter design method for boost-glide missile is proposed. According to the characteristic of boost-glide trajectory, the trajectory is divided into several parts and each part is studied: the relationship between missile parameters and the theoretical velocity is deducted; through simulation, the model used to describe the relationship between parameters of glide starting point and that of engine shutdown point is established; considering the balanced glide condition, the formula to estimate the glide range is obtained. Based on the models, the analytical expression between the missile range and the parameters of the engine shutdown point is given, and the parameter design method for glide missile is established preliminarily.

Boost-glide missile; Weaponry and equipment; Parameter design

V421.1

A

1004-7182(2016)04-0005-04

10.7654/j.issn.1004-7182.20160402

2015-01-06；

2015-02-13

蒋明明（1990-），男，助理工程师，主要研究方向为飞行器设计