吸气式飞行器爬升段轨迹与速度在线规划及制导律设计
赵长见,梁 卓,严佳民,周国峰,韩英宏
(1. 国防科学技术大学,长沙,410073;2. 中国运载火箭技术研究院,北京,100076)
吸气式飞行器爬升段轨迹与速度在线规划及制导律设计
赵长见1,2,梁 卓2,严佳民2,周国峰2,韩英宏2
(1. 国防科学技术大学,长沙,410073;2. 中国运载火箭技术研究院,北京,100076)
由于吸气式飞行器全程在大气层内飞行,飞行弹道极易受到发动机性能偏差、气动偏差和风干扰等影响,导致爬升段初始条件具有较大的不确定性。针对该问题,将轨迹控制回路与速度控制回路作为2个相互独立的回路进行设计,建立了在线轨迹规划与速度规划和导引模型,并以射程最大化为目标,采用拟牛顿法进行多变量寻优,得到需用最优爬升时间和加速时间。最后以典型工况为例进行数学仿真,验证了该方法的合理性与有效性。
吸气式飞行器;爬升段;轨迹规划与控制;速度规划与控制
0 引 言
吸气式飞行器通常采用固体推进剂火箭发动机作为一级动力系统,将飞行器加速至吸气式发动机可正常工作的速度范围。由于吸气式飞行器全程在大气层内飞行,一方面,飞行弹道极易受到发动机性能偏差、气动偏差和风干扰等多项偏差和干扰的影响,导致飞行器一级动力系统耗尽关机点速度、位置和姿态的变化范围较大,从而引起爬升段初始条件具有较大的不确定性;另一方面,吸气式发动机内部参数和性能指标随飞行器的速度、高度、攻角以及实际进入发动机的空气流量的变化而变化,直接影响飞行器的飞行品质[1~5]。针对以上问题,本文采用理论推导与数学仿真相结合的方法,提出以爬升起始时刻的飞行器高度和速度为初始条件、以巡航高度和巡航速度为终端约束条件,在线规划理想轨迹和理想速度曲线,采用闭环比例积分微分(Proportion Integral Derivative,PID)控制器对理想轨迹和速度进行跟踪控制,确保飞行器在多约束、强干扰条件下实现不同弹道段的无缝连接。为便于工程实现,将轨迹控制回路与速度控制回路作为2个相互独立的回路进行设计,相应地存在需用爬升时间和需用加速时间2个设计变量。这2个变量取值直接影响飞行器的射程大小,因此,设计时以飞行器射程倒数为目标函数,采用拟牛顿法进行了变量寻优,使飞行器射程最大化。
1 轨迹在线规划与导引模型
1.1 设计约束
攻角约束范围为[αmin, αmax],αmin与αmax分别为在当前飞行器的飞行高度和马赫数下吸气式发动机正常工作时的最小和最大可用攻角。
1.2 轨迹在线规划
以爬升段的起始和终端条件为约束,采用抛物线规划理想当地弹道倾角曲线:

式中 Θcx和Θ˙cx分别为当地弹道倾角指令与当地弹道倾角变化率指令;k1和k0为系数;t为理论规划时间;t为爬升段终端时间;(t-t)为抛物线的对称轴。
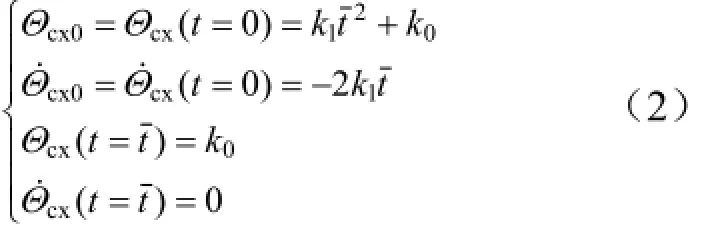
联立式(1)和式(2),得:

Θcx(t=t)为抛物线弹道最高点的函数值,可根据仿真数据确定需要爬升的高度与相应的Θcx(t=t),制作数表装订,在线插值使用。
令式(1)中Θcx= 0,可得到t的解t1和t2:

式中 t1为抛物线左半边函数值零点对应的时间点;t2为飞行器爬升结束时刻的飞行状态。
由于Θcx(0)>0且抛物线右半边是规划的理论角曲线,因此舍去t1解,取t = t2。决定爬升时间的参数为t,该参数可通过优化算法计算得到。
1.3 轨迹导引方法
根据理论推导得到攻角到弹道倾角和高度的传递函数,构建攻角反馈的控制回路,图1给出了轨迹跟踪制导律指令形成过程。
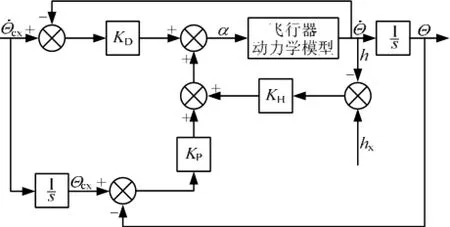
图1 轨迹跟踪制导律指令形成
以攻角为控制变量,采用闭环PID控制律控制飞行器稳定地沿着理想弹道飞行,以实现弹道的平滑过渡。爬升飞行段制导律设计方法描述为
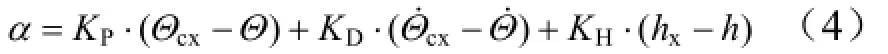
2 速度在线规划与导引模型
2.1 约束条件
吸气式发动机许用推力范围为[Pmin, Pmax]。Pmin与Pmax分别为在当前飞行器的飞行高度、马赫数和攻角特性下吸气式发动机的最小和最大可用推力。
2.2 平衡推力分析
飞行器受力示意图如图2所示,o-xyz、o-x1y1z1和o-xvyvzv分别表示发射坐标系、弹体坐标系和速度坐标系,当不考虑偏航运动时,xoy、x1oy1和xvoyv共面。

图2 飞行器受力示意
由图2可见,飞行器受力包括P,Rxv,Ryv和G[6,7]。欲使飞行器速度保持不变,必须满足飞行器在速度坐标系oxv轴上合力为零,即:

由此求出当前时刻需要的平衡推力PP:

2.3 速度在线规划
以转级点马赫数为起始点约束、以巡航马赫数为终端约束,在线实时生成的加速段理想速度曲线设计如下:

式中 Macx为理想马赫数;Macx-1为前一时刻的理想马赫数;tΔ为计算步长;C表示声速;Δa为飞行器的净加速度,即发动机除去平衡推力外的推力可产生的加速度;m0为飞行器当前质量。为便于实现,Δa可以离散为有限档位,即:

i取值不同时对应不同的净加速度,因此飞行器需用加速时间不同,相应地飞行器射程亦不同,该参数可通过优化算法计算得到。当飞行器速度达到巡航马赫数时,令Δa置零。
2.4 速度导引方法
根据理论推导得到发动机推力到速度的传递函数,构建推力反馈的速度PID控制网络,图3给出了速度控制指令形成过程。
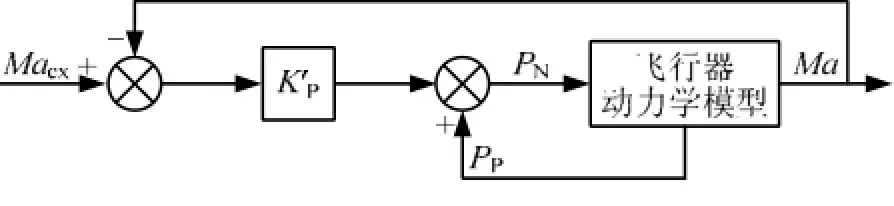
图3 速度控制指令形成
速度导引由闭环的PID控制网络实现,控制量为需用推力,控制方程如下:

3 爬升时间与加速时间优化方法
3.1 优化模型
为便于问题分析,作以下假设:
a)吸气式发动机耗尽关机后,飞行器飞行高度为巡航高度、飞行马赫数为巡航马赫数,因此,飞行器从下压至落地航程一定,射程最大化建模时不考虑此部分航程;
b)飞行器爬升前飞行距离较短,可忽略不计。
基于以上假设,评价飞行器射程能力时,可采用以下简化的等效射程公式:

式中 Sp为飞行器爬升段航程,由弹道计算得到;fi为第i项约束条件,包括可用过载、可用攻角、可用舵偏角、推力使用包络;ηi为第i项约束条件对应的罚因子,当fi满足时ηi为0,否则置一大量;Sx为由巡航段吸气式发动机剩余装药量估算得到的航程。

式中 Δmx为巡航开始时刻吸气式发动机剩余装药质量;0m˙为巡航飞行时飞行器质量变化率;Max为巡航马赫数。
3.2 优化算法
采用拟牛顿法[8]进行求解:令x(n, m)二维矩阵存储爬升时间tp和加速时间ta的值,其中,n取1时,x(1, m)存储tp值,n取2时,x(2, m)存储ta值;m为迭代次数,本文取m =10。
a)选取自变量初值x(n, 0)。
b)采用下述迭代公式进行迭代计算:
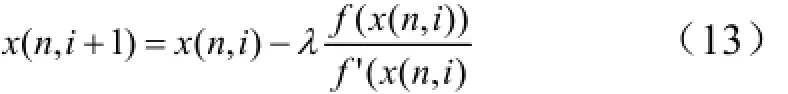
式中 λ为迭代步长系数,可视对象特点优化选取。
c)若满足迭代精度要求时迭代结束,否则返回b)继续迭代。
d)若m>10,但迭代精度不满足要求时,强行退出,采用前一时刻的值作为当前解。本文迭代精度取为10-8,即要求
4 仿真算例与分析
为验证本文所提方法的有效性,采用典型发射条件,在考虑气动偏差、大气干扰、发动机偏差等干扰条件下进行弹道仿真分析,得到主要参数曲线见图4~8所示。对图中曲线的参数进行了归一化处理,以无量纲的相对量形式给出,仅表征参数的变化规律,变量tpN和taN分别为最优爬升时间和最优加速时间,ts1和ts2表示迭代步长。

图4 飞行器的高度-时间曲线

图5 飞行器的马赫数-时间曲线
由图4和图5可以看出,飞行器在多约束强干扰条件下可以稳定地爬升、加速至巡航高度、速度,实现不同弹道段的无缝连接,从而证明了轨迹和速度的在线规划与控制方法的正确性。

图6 飞行器的高度-航程曲线

图7 飞行器的攻角-时间曲线

图8 飞行器的需用推力-时间曲线
由图6可见,基于拟牛顿法进行多变量弹道优化方法可以解算得到最优需用爬升时间和加速时间;图7和图8表明优化得到的需用攻角和需用推力控制量随时间的变化曲线整体比较平稳,从而证明了以爬升时间与加速时间优化方法进行弹道优化的有效性。
5 结束语
本文采用理论推导与数学仿真相结合的方法,提出一种吸气式飞行器爬升段轨迹与速度快速在线规划方法,确保了飞行器在多约束强干扰条件下平稳跟踪在线生成的理想弹道轨迹和理想速度曲线,实现了不同弹道段的无缝连接。在此基础上提出基于拟牛顿法进行多变量弹道优化的方法,得到了最优需用爬升时间和加速时间,使得飞行器射程最大化。吸气式飞行器爬升段轨迹与速度在线规划及制导律模型及其最优爬升时间与加速时间解算方法算法简单、自适应性强,具有一定的工程应用价值。
[1] 尚腾, 谷良贤, 赵吉松. 冲压发动机导弹爬升轨迹与推力调节规律优化[J]. 飞行力学, 2012,30(3): 280-283.
[2] 刘恒军, 沙建科, 王华. 冲压发动机导弹弹道多目标优化[J]. 系统仿真学报, 2009,21(9): 2764-2766.
[3] 侯宏录, 柳长安, 周德云. 巡航导弹加速爬升段弹道优化设计[J]. 飞行力学, 2006,24(1): 45-47.
[4] 王华, 杨存富, 刘恒军. 冲压发动机为动力导弹爬升弹道优化[J]. 弹箭与制导学报, 2008,28(3): 185-188.
[5] 施雨阳, 万自明, 徐敏. 冲压发动机导弹爬升轨迹: 发动机一体优化设计[J]. 计算机仿真, 2013,30(10): 138-142.
[6] 钱杏芳, 林瑞雄, 赵亚男. 导弹飞行力学[M]. 北京: 北京理工大学出版社, 2000.
[7] 赵汉元. 飞行器再入动力学和制导[M]. 长沙: 国防科技大学出版社, 1997.
[8] 陈宝林. 最优化理论与算法[M]. 第2版. 北京: 清华大学出版社, 2005.
Design of Driving Down-Phase Guidance Law for Air-Breathing Vehicles Based on Single Attack Angle Characteristics
Zhao Chang-jian1,2, Liang Zhuo2, Yan Jia-min2, Zhou Guo-feng2, Han Ying-hong2
(1. National University of Defense Technology, Changsha, 410073; 2. China Academy of Launch Vehicle Technology, Beijing, 100076)
Considering endo-atmosphere flight, the air-breathing vehicles is liable to be affected by the engine performance, aerodynamic force, windage, etc. Therefore, initialization of climb trajectory is uncertain. Aiming at this question, trajectory control loop and speed control loop are designed independently. In order to achieve maximum range, a quasi-Newton algorithm is proposed to automatically optimize the climb time and stepped-up time. Then simulations are carried out under some typical conditions, and the simulation results confirm its validity and rationality.
Air-breathing vehicles; Climb phase; Trajectory design and control; Speed design and control
V448
A
1004-7182(2016)04-0008-04
10.7654/j.issn.1004-7182.20160403
2015-08-26;
2016-02-19
赵长见(1976-),博士,研究员,主要研究方向为飞行器总体设计及控制技术

