通用高速飞行器预测校正再入制导方法研究

宋剑爽，胡 钰，洪 蓓，熊 伟，王 智

（北京宇航系统工程研究所，北京，100076）

通用高速飞行器预测校正再入制导方法研究

宋剑爽，胡 钰，洪 蓓，熊 伟，王 智

（北京宇航系统工程研究所，北京，100076）

给出一种适合通用高速飞行器（CAV）的预测校正再入制导方法。首先基于再入高速飞行器三自由度运动模型，研究了再入过程中CAV受到的过程约束。基于准平衡滑翔条件给出了在指定倾侧角下的参考航程的计算方法，并指出当飞行器的初始航程超过参考航程时，可以使用本文给出的方法有效抑制飞行器轨迹在高度上的振荡。为了提高制导精度，不仅给出了精确计算当前倾侧角的方法，也给出了粗略调整终端倾侧角方法。最后仿真验证了制导方法的有效性。

通用高速飞行器；准平衡滑翔条件；航程预测；预测校正制导

0 引 言

通用高速飞行器（Common Aero Vehicle，CAV）具有较大的升阻比，可以在大气层内进行长距离无动力滑翔飞行，实现远程快速打击。尽管HTV-2已经进行了2次试飞，但是再入制导依然存在很多挑战，如何获得有效的最优弹道剖面是再入制导研究的热点。高速飞行器再入飞行制导方法一般分为标准轨道制导方法和在线预测校正制导方法。标准轨道制导方法制导需要设计控制器跟踪离线设计的标准轨迹，虽然所用导引率简单，但是攻角需要跟随跟踪控制率围绕参考剖面进行小范围调节[1,2]。随着机载计算机技术的发展，在线预测校正制导方法逐渐成为了一种有效的制导方式。

传统的在线预测校正制导方法首先需要根据航程设定好攻角剖面，这样就可以通过调整倾侧角的大小和符号实现对飞行器的精确制导。但是基于这种方法容易产生一个高度方向上强烈振荡的弹道，给飞行器控制器设计带来很大挑战。文献[3]给出了一种基于准平衡滑翔条件（Quasi Equilibrium Gliding Conditions，QEGC）抑制轨道振荡的方法，但是仿真发现这种抑制效果仅仅在某个特定航程范围内有效。

本文给出了一种适合再入高速飞行器的在线预测校正制导方法。为了方便对飞行器航程进行估计，基于QEGC提出一种评估CAV航程的方法。当CAV的初始航程在指定航程附近时，可以使用本文给出的方法有效抑制飞行器轨迹在高度方向上的振荡。由于落点精度的要求，CAV飞行对再入终端的倾侧角约束较弱，而对终端位置约束要求较高。当CAV靠近目标点时，CAV剩余航程随时间变化的速率需要有针对性的调整，并放宽准平衡滑翔约束，使CAV具有更大的机动空间，从而减小终端制导误差。

1 制导模型及约束

1.1 再入高速飞行器运动模型

考虑地球自转的再入高速飞行器三自由度运动模型为[3]

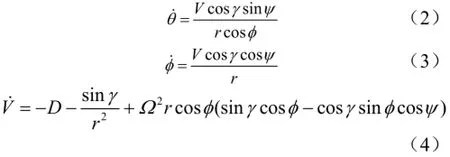
式中 r为飞行器到地心的距离；θ 和φ 分别为飞行器当前所处的经度和纬度；V为飞行器相对于地球的速度；γ 和ψ 分别为航迹角和航向角；σ 为倾侧角；Ω为地球自转角速度。为了计算方便，仿真时间可以使用tscale=进行无量纲化处理，仿真中用到的长度可以使用地球半径R0进行无量纲化处理，而无量纲化的速度为整个制导模型的控制输入。

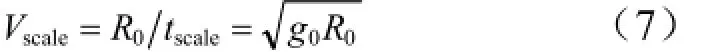
其中，g0= 9.81 m/s2，R0= 6 378 135 m。无量纲化的升力、阻力的表现形式分别为[4]

式中 M为飞行器的质量；ρ 为飞行器所处的大气密度；Aref为飞行器的参考面积；CL和CD分别为飞行器的升力系数和阻力系数。

飞行器剩余航程s无量纲化的表现形式为

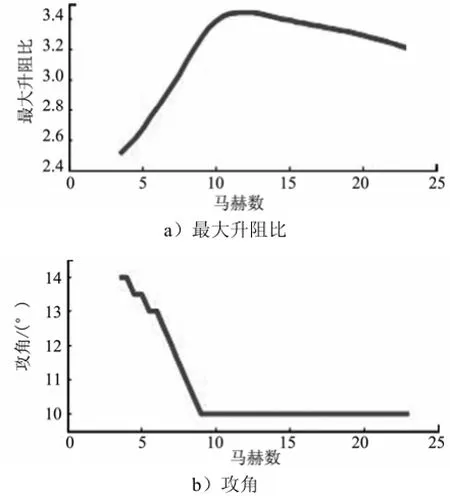
图1 最大升阻比曲线以及其对应的攻角剖面

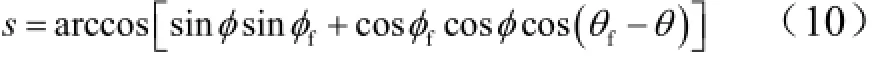
式中 φf和θf分别为终端经度和终端纬度。忽略航向误差，剩余航程对时间的导数为

当时间在仿真中不是一个必需的变量时，1个类能量的变量e在仿真中可以被用来作为1个独立变量使用，表达式为

1.2 制导约束

CAV再入过程中受到的约束分为过程约束和终端约束。过程约束主要有热流约束maxQ˙，过载约束nmax，动压约束qmax和准平衡滑翔约束[6,7]，这些约束的表达式为

当地球自转变量被忽略时，e的导数可以表示为

由于D和V均为正值，式（12）是一个大于零的量，此时e是恒增量。

式（1）～（6）和式（9）就是制导过程中需要的仿真模型。使用文献[5]中的气动模型进行了验证，本文给出的制导方法的有效性。图1给出了最大升阻比剖面以及其对应的攻角剖面。此时倾侧角和攻角就是

式中 kQ= 9.4369×10-5。

根据QEGC，γ和γ˙都是小量，忽略地球自转可以得到新的过程约束：

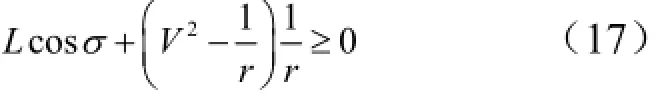
给出1个速度值，通过式（14）～式（16）可以获得对应的高度值，当给出一系列速度值时就可以绘制出3条曲线。当1个满足准平衡滑翔条件的动常值倾侧角σQEGC给出时，基于不等式（17）可以获得1条新的曲线。式（14）～式（16）是CAV再入过程中必须满足的条件，而式（17）是一个软约束，因此这个不等式仅仅是一个参考约束。

CAV常见的终端约束主要有飞行器终端的高度、速度和位置满足终端要求，用下式来表示：

基于QEGC并忽略地球自转的影响，式（5）可以简化为

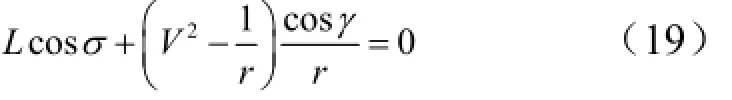
或者

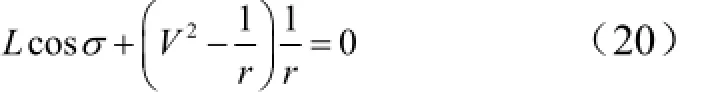
2 预测制导

分析式（1）～式（6）和式（10）不难发现当忽略地球自转因素影响时，式（1）、式（4）、式（5）和式（11）可以作为纵向制导模型仿真。由于在纵向制导模型中，时间不是必需的变量，可以使用e代替；当速度V被用到时可以使用V=代替；则新的纵向制导模型为

由于QEGC，在CAV滑翔再入制导开始时γ 的值为小量，则倾侧角可以表示为能量e的线性函数形式：

当初始时刻σf给出时，纵向预测制导就变成获取当前的倾侧角σcur的单变量的非线性函数求解问题，即适时获得σcur使得下式成立：

式中 Δserror为允许最小误差。

预测制导校正算法就是使用当前的倾侧角剖面通过从当前的系统状态定积分式（21）～式（23）到e=ef*；当s()≠时，可以基于割线法获得新的σcur：

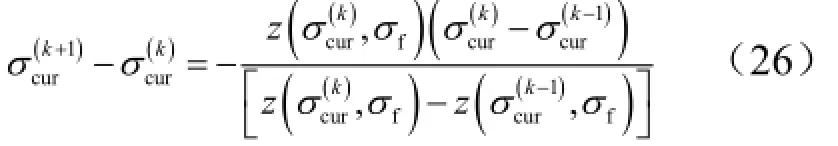
2.1 横侧向制导

横侧向制导率的设计是适时地给出倾侧角的符号，即设定倾侧角的反转逻辑。限制航向角跟踪视线角的误差可有效地实现对制导横程的控制。假设当前的经度、纬度分别为θ 和φ，则此时飞行器和目标的视线角为

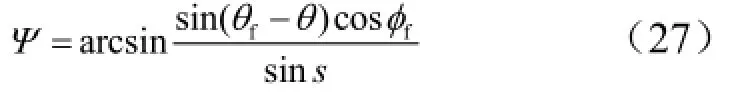
定义航向角的偏差ΔΨ = ψ -Ψ，其中，ψ 为航向角，Ψ 为视线角。图2为航向角误差边界，当航向角偏差的绝对值超过了图2中所示的边界值时，倾侧角的符号改变；当航向角误差绝对值不大于误差边界时，倾侧角的符号保持不变。

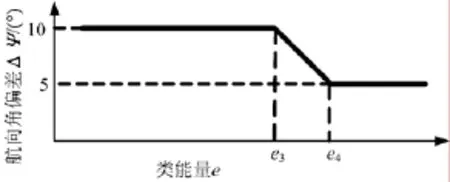
图2 航向角误差边界

2.2 轨迹修正

由式（1）可知当航迹角出现轻微波动时会使高度出现很大波动，但是这种波动对飞行器的控制影响很大，需要采用措施抑制。当飞行器滑翔过程中航迹角保持不变或者微量变化时，能有效抑制高度的波动，即需要保证0γ=˙。由式（5）可知调整Lcosσ 的值可以实现对γ˙的有效控制[3]：

式中 σbase为预测得到的倾侧角；σnew为新的倾侧角；h˙为当前的高度变化率；refr˙为参考速度变化率；rk˙为增益。当高度的变化率大于参考值时，其根本原因是航迹角大于参考值引起的，这样可以减小式（5）中的Lcosσbase值来实现对γ˙变化的抑制。

由式（1）可知：

式中 γQEGC为满足准平衡滑翔条件的动常值航迹角。设定式（20）中σ = σQEGC，假设瞬时升力系数CL不随时间变化，对式（20）求导可以得到：

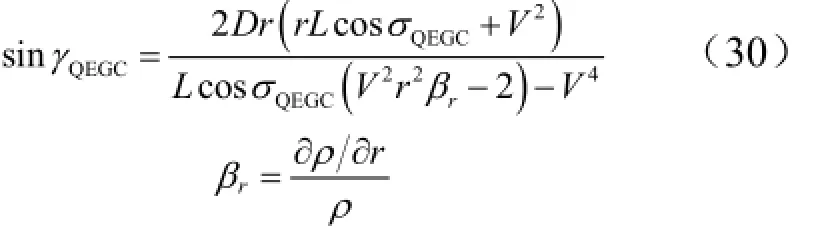
由于制导过程中无量纲的1r≈，式（30）可以进一步简化得到：

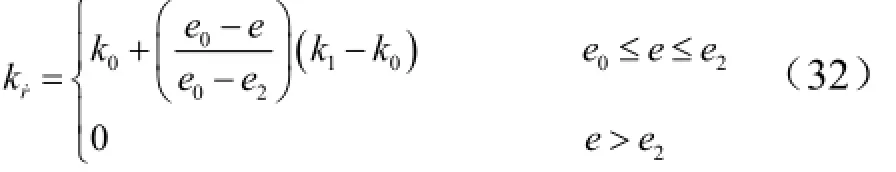
把式（31）代入式（29）可以得到高度变化速率的参考值。为了实现对再入轨迹的调整，这里设置rk˙为能量e的表达式：式中 k0= 20；k1= 0～0.5k0。当靠近制导终点时，为了获得精确的预测值本文修正终端选为e2，这样当能量大于e2时直接使用预测得到的倾侧角值，从而保证终端误差在允许范围内。

仿真发现仅通过上面给出的方法很难实现对再入轨迹跳变的抑制，原因在于初始航程设置与σQEGC设置不匹配。假设0γ=˙，则式（21）中的cosγ 可由式（19）得到：

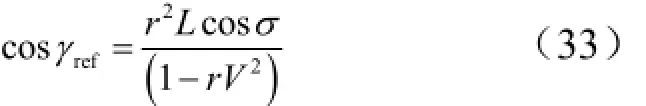
此时，式（21）变为

可通过式（20）获得QEGC的参考飞行轨迹的高度-速度剖面。设定式（33）中的σ = σQEGC，利用参考高度-速度剖面获得参考航程Δsref。这里获得的Δsref仅是一个参考量，实际应用中初始航程设置应该略大于这个值。

2.3 终端制导参数修正

飞行器接近终点仅仅调整当前的倾侧角无法满足制导精度时，可以通过调整σf提高制导精度。当预测得到的最小z(σ0, σf)无法满足式（25）时，假设ds/de随能量e呈现线性变化的趋势。则新的σf可以使用下式计算得到

式中 (CL/CD)f为终端飞行器的升阻比；σfcmd为式（24）中新的σf。

3 仿真分析

不同于标准轨道制导方法制导，当飞行器的气动参数出现误差使飞行器轨迹出现偏差时，在线预测校正制导法能通过对下一时刻的倾侧角大小和符号预测过程中抵消这种偏差带来的影响。下面在不同航程下使用本文给出的制导方法进行仿真[5]。

本文选用的制导初始条件：高度为60 km，速度为7.01 km/s，经度、纬度为 (0°, 0°)，航迹角为-0.05°，航向角为57.48°。设定制导终端的高度和速度大小分别为28 km和2 km/s，设定σQEGC= 15°；可以计算得到此时无量纲下的参考航程为Δsref= 2.416 2。

为了验证本文给出的制导方法的正确性，表1给出了2个制导终端（弹道1和弹道2）的经度、纬度。

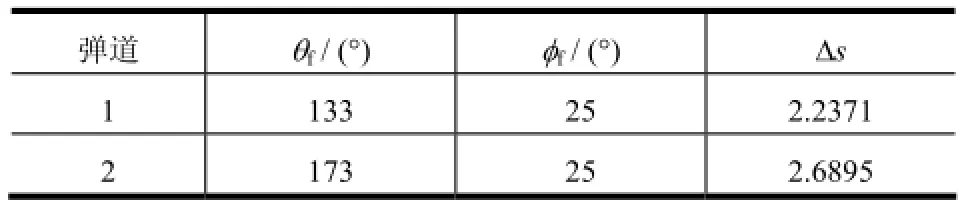
表1 制导终端经度、纬度约束及其对应的初始航程

图3为弹道1速度-高度剖面，图4为弹道2速度-高度剖面示意。由于弹道1的初始航程小于参考航程，由图3的仿真结果中发现使用本文给出的弹道修正方法对弹道1振荡的抑制作用很小。

图3 弹道1速度-高度剖面示意

图4 所示弹道的初始航程大于参考航程，在保证过程约束和终端约束的前提下，本文给出的弹道修正方法能有效抑制振荡。

图4 弹道2速度-高度剖面示意

4 结束语

本文提出了一种针对CAV的在线预测校正制导方法，该方法以在线实时调整当前倾侧角的值和符号为主要控制手段，并通过预测初始航程使本文给出的弹道修正方法能有效抑制弹道在高度上的振荡。此外，为了减小预测误差以及初始设定的终端倾侧角值对飞行器终端约束的影响，给出了一种有效调整终端倾侧角的方法，从而进一步减小了终端预测误差。最终通过仿真验证了制导方法的有效性。

[1] Harpold J C, Graves C A. Shuttle entry guidance[J]. Journal of Astronautical Sciences, 1979,37(3): 239-268.

[2] Harpold J C, Gavert D E. Space shuttle entry guidance performance results[J]. Journal of Guidance, Control, and Dynamics, 1983(6): 442-447.

[3] Lu P. Entry guidance: a unified method[J]. Journal of Guidance, Control, and Dynamics, 2014,37(3): 713-728.

[4] 梁子璇, 任章. 基于在线气动参数修正的预测制导方法[J]. 北京航空航天大学学报, 2013,39(7): 853-857.

[5] Phillips T. A common aero vehicle (CAV) model, description, and employment guide[M]. Schafer Corporation for Air Force Research Laboratory and Air Force Space Command, 2003.

[6] Shen, Z, Lu P. Onboard generation of three-dimensional constrained entry trajectories[J]. Journal of Guidance, control, and Dynamics, 2003,26(1): 111-121.

[7] Xue S, Lu P. Constrained predictor-corrector entry guidance[J]. Journal of Guidance, Control, and Dynamics, 2010,33(4): 1273-1281.

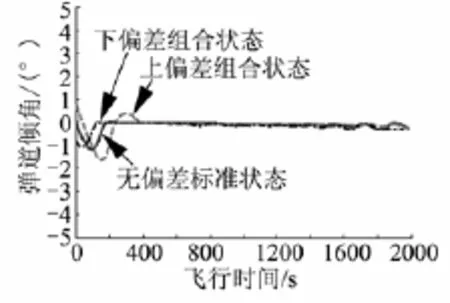
图8 不同组合偏差工况下弹道倾角随飞行时间变化关系

由图7、图8及表2可知，模糊逻辑控制律鲁棒性较好，能够满足各种偏差工况下的高精度拟平衡飞行要求，始终将弹道倾角控制在0°附近。

5 结束语

本文针对模糊逻辑以及遗传算法的特点，将定性分析和定量优化进行集成，采用遗传算法对模糊逻辑控制器进行离线优化处理后，即可用于拟平衡飞行的在线控制，其控制律形式简单，具有最优控制性能，对于各种偏差或干扰工况的鲁棒性较好、智能化程度较高。通过设计不同的性能指标函数，可以实现不同的控制功能，具有一定的适用范围。后续将采用更加贴近实际的精确弹道计算模型对提出的模糊逻辑控制律进行仿真验证，同时进一步研究将模糊逻辑控制律用于横向机动的可行性，为解决再入飞行控制提供了新思路。

参 考 文 献

[1] 刘欣. 滑翔式飞行器再入弹道设计[J]. 弹箭与制导学报, 2011, 31(6): 161-162.

[2] 卢宝刚. 基于拟平衡滑翔的数值预测再入轨迹规划算法[J]. 哈尔滨工业大学学报, 2015, 47(1): 14-15.

[3] 朱凯. 滑翔导弹再入制导与控制方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2011.

[4] 周锐. 基于进化策略的导弹模糊制导律设计[J]. 宇航学报, 2004, 25(4): 449-451.

[5] 阮春荣. 大气中飞行的最优轨迹[M]. 北京: 宇航出版社, 1987.

[6] 杨炳尉. 标准大气参数的公式表示[J]. 宇航学报, 1983, (1): 83-86.

[7] 薛定宇. 控制系统计算机辅助设计—MATLAB语言与应用[M]. 北京:清华大学出版社, 2006.

[8] Choi D H, Oh S Y. A new mutation rule for evolutionary programming motivated from backproagation learning[J]. IEEE Transactions on Evolutionary Computation, 2000, 4(2): 188-190.

[9] Phillips T H. A common aero vehicle (CAV) model, description, and employment Guide[R]. Schafer Corporation, 2003.

Predictor-corrector Guidance for Common Aero Vehicle

Song Jian-shuang, Hu Yu, Hong Bei, Xiong Wei, Wang Zhi
(Beijing Institute of Astronautical Systems Engineering, Beijing, 100076)

In this paper, a predictor-corrector guidance method for Common Aero Vehicle (CAV) is presented. First of all, the path constraints of reentry guidance is presented based on the three-dimensional equations of motion of a gliding vehicle. Then, a method of calculating initial reference range is proposed on the base of the quasi-equilibrium glide condition. If the reference range is exceeded by the initial range, the fluctuations of height will be suppressed by use of the guidance method proposed. The algorithm of calculating the value of current bank angle and terminal bank angle is proposed. The simulation is used to validate the guidance method in the last.

Common aero vehicle; Quasi-equilibrium glide condition; Prediction of flight range; Predictor-corrector guidance

TJ765.1

A

1004-7182(2016)04-0034-05

10.7654/j.issn.1004-7182.20160409

2015-10-13；修改日期：2016-02-23

宋剑爽（1983-），男，博士，工程师，主要研究方向为轨道设计、制导设计