机动飞行器的效能影响因素分析
化 金,王立旭,朱学昌
(北京宇航系统工程研究所,北京,100076)
机动飞行器的效能影响因素分析
化 金,王立旭,朱学昌
(北京宇航系统工程研究所,北京,100076)
针对防御系统目标跟踪和轨迹预报的原理,分析目标机动参数对估计误差和预报误差的影响因素,以及预报误差对拦截飞行器脱靶量的影响。以脱靶量为指标,分析目标机动的效能。研究结果表明,增加机动加速度大小、增加机动持续时间、选择合适的机动开始时刻可以增加估计误差与预报误差,从而增加脱靶量,提高目标机动的效能。
目标跟踪;轨迹预报;机动参数
0 引 言
机动飞行是一种的常见的飞行方式,影响机动飞行器躲避拦截效果的因素需要详细分析。本文定义描述机动飞行的机动参数,分析机动参数变化对轨迹预报误差的影响,根据误差传播的两种途径分析预报误差对脱靶量的影响,最后以脱靶量为指标分析机动参数变化对机动飞行器效能的影响。
1 预报误差的产生及传播
雷达的探测误差和滤波算法的模型误差导致了估计误差的产生,估计参数作为轨迹预报的初值,致使预报结果产生误差。图1描述了防御系统中误差信息传播方向,从图1中可以看出,预报误差具有两种传播途径:
a)在拦截飞行器发射前,指控系统将不精确的初始数据装订给拦截飞行器,导致拦截飞行器在中制导开始时刻存在较大偏差;
b)在拦截飞行器中制导飞行时,制导系统利用不精确的导引信息修正轨迹,使拦截飞行器在中、末制导交班时偏离零控拦截状态。拦截飞行器在有限的机动能力下无法将零控脱靶量修正到很小的范围,从而导致拦截失败。

图1 防御系统信息传播示意
2 机动飞行对预报误差的影响分析
设定目标在飞行中段从某时刻起沿射面的法线方向(弹道坐标系下的Z向)进行方波机动(机动过载为方波),机动持续一段时间后回到原射面内继续惯性飞行。不同时刻的机动加速度(除重力外飞行器所受合力的加速度)的表达式如下:
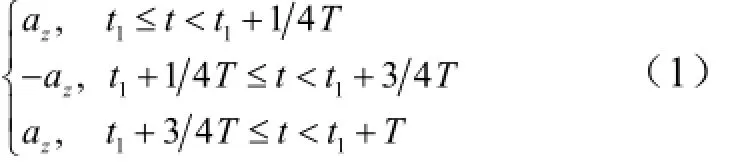
式中 az为机动加速度;T为机动持续时间;t1为机动开始时刻。这3个参数是本文描述机动飞行的机动参数。
2.1 轨迹估计误差分析
本文采用扩展卡尔曼滤波算法[1,2](Extended Kalman Filter,EKF)对目标的轨迹参数进行估计,用Singer模型[3]描述机动目标运动,选择雷达坐标系[4](北天东坐标系)的斜距、俯仰角和方位角构成测量向量,雷达的探测精度用测距精度σr和测角精度σa表示。目标在发射坐标系下的位移、速度、机动加速度构成目标状态向量X = [x, y, z, vx, vy, vz, ajx, ajy, ajz]T,估计参数向量为,估计误差ΔX为目标轨迹估计参数X~与真实参数X的差值,即:

在雷达的测距精度和测角精度固定的情况下,分别改变3个机动参数的取值,通过仿真得到机动前后一段时间内的估计误差,分析机动参数变化与估计误差变化的规律。由于目标在Z向做方波机动,所以图2只显示Z向位移误差Δz的仿真结果。仿真分析参数的相对取值如表1所示。

表1 仿真参数设置
从图2可以看出,在目标机动飞行之前,雷达稳定跟踪目标,Δz在0附近很小的范围内波动。从t1到(t1+2T) 的时间段内,Δz波动幅度增大,出现了3个极值点,第2个极值点的绝对值最大,达到了峰值,第3个极值点出现在结束机动飞行之后的某个时刻。Δz的大幅波动可以用峰值和持续时间来描述。由图2a可知,Δz的峰值随az增大在显著增大,但是持续时间没有发生明显变化;由图2b可知,当az和t1相等时,Δz的峰值随T的增加而显著增加,持续时间也相对变长;由图2c可知,改变t1,Δz的峰值和持续时间均无明显改变。
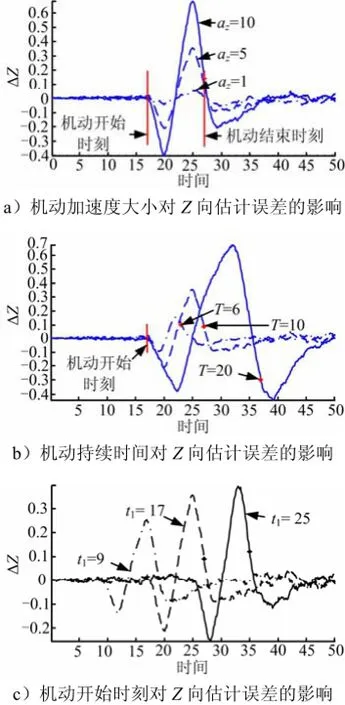
图2 机动参数对估计误差的影响
由上述综合分析可知:a)机动飞行可以增加防御系统估计误差;b)估计误差大幅波动从机动开始时刻开始,在停止机动的一段时间之后结束,可以通过改变机动开始时刻,改变估计误差大幅波动的开始时刻;c)可以通过增加机动加速度大小或者机动持续时间,增加估计误差的峰值;d)可以通过增加机动持续时间,增加估计误差大幅波动的持续时间。
2.2 轨迹预报误差分析
轨迹预报是根据估计得到的目标位置、速度等方面的信息,对目标在后续时刻的轨迹进行合理有效的估计[5]。本文以预报开始时刻t2的估计参数为初值,对Singer模型的动力学方程组进行数值积分,得到预报时间T2内所有的轨迹参数。同时,利用协方差分析描述函数法[6,7](Covariance Analysis Describing Function Technique,CADET)对预报误差的协方差进行计算,表达式为

式中 ()tN为动力学方程组ˆ()f t的偏导数矩阵,;ˆ()tX为状态变量的预报值;()tP为状态变量的误差协方差矩阵;()tQ为系统噪声方差矩阵。定义预报误差向量为ˆˆ Δ=-XXX,Z向预报误差为ˆzΔ。在目标非机动飞行的情况下,以预报误差的均值为轴线、协方差为边界的误差通道[8]如图3所示。

图3 非机动时轨迹预报误差通道
从图3可以看出,对于非机动飞行,预报误差的均值随时间变化很小,但协方差随着预报时间的增加而明显增大,说明预报时间越长轨迹预报越不精确。
分别改变3个机动参数的取值,比较预报误差均值与协方差的变化,分析机动参数变化对轨迹预报误差的影响,仿真结果如图4所示。仿真分析参数的相对取值如表2所示。

表2 仿真参数设置
从图4可以看出,机动飞行可以显著增加轨迹预报的误差,图中误差通道的上下边界几乎与轴线重合,说明协方差的变化明显小于均值的变化,因此只需分析机动参数对轨迹预报误差均值的影响。图4a和图4b中的曲线显示,增加az和T可以显著增加ˆzΔ,这是由于t2时刻机动飞行引发轨迹参数估计误差的增大,这个误差在积分过程中不断的累积,导致一段时间后预报参数严重不精确。图4c中,t2与t1和 (t1+T) 的关系不同,ˆzΔ的变化幅度也不同,t1= 9时误差通道逐渐偏离0值,说明t2>t1+T时,估计误差的大幅波动还未结束,导致ˆzΔ增大;t1= 25时误差通道保持在0值附近,说明t2<t1时,由于机动前的估计误差波动幅值很小,导致ˆzΔ的增加不明显;t1=17时误差通道迅速偏离0值,说明t1<t2<t1+T时,预报算法的模型不能准确描述运动规律,导致ˆzΔ明显增加。

图4 机动参数对轨迹预报误差的影响
综合分析可知:a)无论目标是否机动飞行,轨迹预报误差的协方差都会随着预报时间增加而增大,而预报时间是依据杀伤区确定的,当目标机动距离相比拦截半径较小时,机动飞行无法延长预报时间,所以机动飞行对预报误差的影响主要体现在误差的均值上;b)在预报时间相同、机动开始时刻相同的情况下,可以通过增加机动加速度和持续时间来增加轨迹预报误差的均值;c)在机动加速度大小和持续时间相同的情况下,改变机动开始时刻,使防御方的预报开始时刻处于目标机动开始与机动停止之间,机动飞行引发防御系统预报误差增大的效果最好。
3 预报误差对脱靶量的影响分析
在拦截飞行器发射前,指控系统根据估计和预报结果装订目标的预测命中点信息,拦截飞行器的制导控制系统在中制导段根据雷达探测信息、更新目标的预测命中点信息,形成制导指令。预测命中点的轨迹预报精度对于拦截效果有很大的影响。图5分别分析拦截飞行器发射时刻t3、中制导段开始时刻t4的预测命中点误差对于脱靶量的影响。

图5 预测命中点误差对拦截飞行器脱靶量的影响
由图5可知,在有限的可用过载限制下,预报误差增大到一定程度后,脱靶量急剧增加,拦截失败。比较图5中的2条曲线可以发现,预报误差相同的情况下,t4时刻的误差比t3时刻的误差引起的脱靶量大,这是因为t3时刻的预报误差可以通过中制导和末制导来修正,而t4的预报误差只能通过末制导修正。相应地,如果增加脱靶量到相同的数值,需要信息处理系统在t3时刻传递更大的预报误差。拦截飞行器修正发射时刻预报误差的能力强于修正中制导段预报误差的能力。
4 机动飞行的效能分析
通过以上的分析可以看出,机动飞行使防御系统的估计和预报误差增大,信息处理系统向拦截飞行器传递不准确的目标信息,导致脱靶量增加,拦截失败。根据预报误差传递的2个途径,仿真场景中设定目标分别在如下时刻横向机动:场景1,拦截飞行器发射时刻;场景2,拦截飞行器中制导起始时刻;场景3,拦截飞行器发射时刻和中制导起始时刻,如图6所示。由图6可知,为排除拦截飞行器自身机动能力不足导致脱靶的情况,仿真分析时将每条机动飞行的标准参数通过信息处理系统传递给拦截飞行器,计算其脱靶量,作为对比参数。
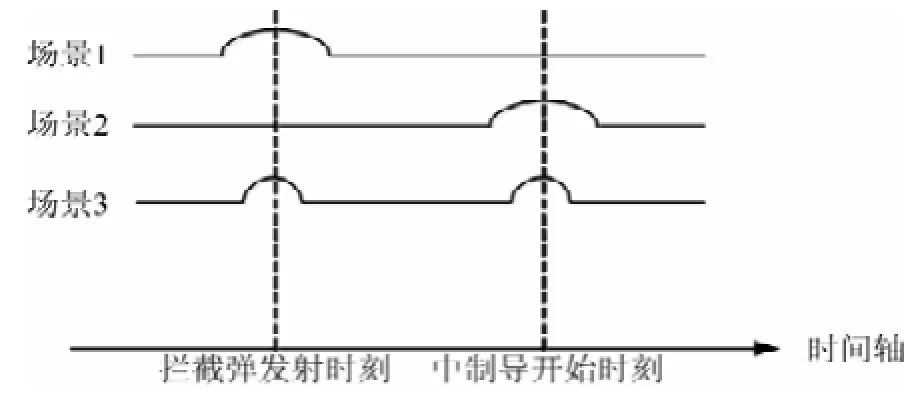
图6 目标横向机动示意
仿真结果的相对值见表3。

表3 机动飞行对脱靶量影响的仿真结果
机动参数相同的条件下,相比标准轨迹参数,防御系统利用估计轨迹参数得到的脱靶量更大,说明在拦截飞行器自身机动能力一定的情况下,估计和预报误差会在一定程度上增加脱靶量。
在机动开始时刻相同的情况下,由表3可以看出,加大机动加速度大小和延长机动持续时间都能增大脱靶量,这是由于防御系统预报开始时刻处于目标的机动飞行过程中,而机动飞行增加了预报开始时刻的预报误差,进而增加了脱靶量,提高了机动飞行效能。在机动加速度和机动持续时间相同的情况下,场景1估计轨迹的脱靶量大于场景2,这是因为防御系统在拦截飞行器发射时刻的预报时间更长,预测命中点的误差更大,而拦截飞行器修正发射时刻预报误差的能力更强。因此需要通过仿真来比较预测误差与修正能力大小,得到拦截飞行器修正误差的效果。
在本文仿真场景中,拦截飞行器修正发射时刻预报误差的效果比修正中制导开始时刻预报误差的效果差,所以场景1比场景2的脱靶量大,场景1中机动飞行的效能更大。场景3中,目标2次机动飞行,使发射时刻和中制导开始时刻的预报误差都增加了,仿真结果表明拦截飞行器的修正效果优于前2个场景,所以场景3的脱靶量最小,此次机动飞行的效能最小。当机动加速度取5、机动持续时间取20,机动开始时刻选为拦截飞行器发射之前,并在拦截飞行器发射后继续机动,脱靶量最大,相比较其他机动参数的组合,这次机动飞行的效能是最大的。
5 结 论
本文从轨迹预报误差传播的角度,以脱靶量为指标分析了机动参数变化对机动飞行效能的影响。研究结果说明,机动飞行使防御系统估计误差大幅波动,增大机动加速度和延长机动持续时间可使波动的峰值与持续时间增加;预报时间、机动加速度、机动持续时间增加都会增大轨迹预报误差;选择机动开始时刻使防御系统的预报开始时刻处于机动飞行期间可以显著增大轨迹预报误差的幅值;拦截飞行器修正发射时刻预报误差的能力强于修正中制导段预报误差的能力;改变机动参数可以使脱靶量增加,从而提高机动飞行的效能。
[1] 秦永元. 卡尔曼滤波与组合导航原理[M]. 西安: 西北工业大学出版社, 2012.
[2] 安志忠, 王东进. 多站雷达中机动目标高精度跟踪分析[J]. 系统工程与电子技术, 2004,26(1): 14-17.
[3] 周宏仁. 机动目标跟踪[M]. 北京: 国防工业出版社, 1991.
[4] 张远, 陈勇, 吴昊. 弹道导弹落点预报方法研究[J]. 导弹与航天运载技术, 2014(3): 5-10.
[5] 孟璇,陈万春. 战术弹道导弹再入段估计与轨迹预报研究: 2005年中国飞行力学学术年会, 桂林, 2005[C]. 2005.
[6] Wang X S, Xie H. Simulation of Covariance Analysis Describing Equation Technique(CADET) in missile hit probability calculation: 2010 Sixth International Conference on Natural Computation, Yantai, 2010[C]. 2010.
[7] 柴华, 杏建军, 唐国金. 基于协方差分析描述函数技术的弹道导弹落点预报[J]. 导弹与航天运载技术, 2011(4):37-40.
[8] 孟凡坤, 吴楠, 牛朝阳. 机动弹道对抗导弹防御系统的效能分析[J]. 飞行器测控学报, 2014,33(5): 399-405.
Effectiveness Affecting Factors Analysis of Maneuvering Flight Vehicle
Hua Jin, Wang Li-xu, Zhu Xue-chang
(Beijing Institute of Astronautical Systems Engineering, Beijing, 100076)
According to principle of target tracking and trajectory predicting, the affecting factors of maneuvering parameters on estimation and prediction errors are analyzed, so is the influence of prediction error on intercepting miss distance. The miss distance is chosen to be the standard to analyze the effectiveness of target maneuvering. Research results demonstrate that increasing maneuvering acceleration, increasing persisting time, choosing appropriate start time will increase estimation error and prediction error, as well as increasing miss distance, so as to improve effectiveness of target maneuvering.
Target tracking; Trajectory predicting; Maneuvering parameters
V57
A
1004-7182(2016)04-0091-05
10.7654/j.issn.1004-7182.20160423
2015-03-09;
2016-06-27
化 金(1991-),女,助理工程师,主要研究方向为飞行器设计

