燃气站点埋地管道变形的数值分析

苏文献，邓　蕾，李　旭，邬晓敏

(1.上海理工大学 能源与动力工程学院，上海200093； 2.上海天然气管网有限公司，上海201204 )①



燃气站点埋地管道变形的数值分析

苏文献1，邓蕾1，李旭1，邬晓敏2

(1.上海理工大学 能源与动力工程学院，上海200093； 2.上海天然气管网有限公司，上海201204 )①

摘要：基于土壤特性、考虑管与土之间的非线性接触作用，采用ANSYS软件对燃气输送站内埋管受土壤冻胀的影响进行热力耦合分析，并校核应力强度。与实测数据的对比表明该种模拟方法具有一定可行性。利用控制变量法对埋管在不同直径、埋深、回填土夯实度和含水率的情况下的应力分布与位移情况进行分析，发现土壤含水率对埋管受冻胀作用的影响较大。

关键词：埋地管道；变形；数值模拟

作为天然气干线长距离输运的终点站，配气站负责将长输管线输运而来的超高压燃气进行除尘净化、调压计量、质量检测与添臭处理等，再经逐级降压至规定值后供居民用户使用[1]。随着燃气需求量的不断增长，干线压力逐步上升，当流经站内调压装置之后，会发生节流效应(焦耳-汤姆逊效应)导致气体的温度降低，冬季时调压(降低)后的燃气温度经常远低于零点[2]。在低温气体作用下，埋管周围的土壤发生冻胀，使得管线发生显著的变形，给燃气站点的安全平稳运行造成隐患。目前，对于燃气站点内的管道冻胀问题方面的研究文献还很少[3]。结合工程实例，利用有限元分析软件建立管-土系统模型，并考虑管与土之间的非线性接触和土壤特性，对站内管线受管内低温影响所发生的冻胀进行分析讨论，为燃气站点的设计提供理论依据。

1数值建模

1.1基本假设

由于土壤冻结时，其微观作用较为复杂，为简化计算并且反映出其主要特性，对管-土模型提出了如下基本假设：

1)忽略土体表面外部载荷的干扰。

2)土壤为匀质、连续的各向同性体。

3)忽略土壤与大气之间辐射传热以及其内部的对流传热。

4)不计土壤中水迁移对温度分布的影响，即只分析原位冻胀。

5)只考虑冰水相变所导致的冻胀对土壤中应力场的影响。

1.2力学与热性能参数的确定

该燃气站所建区域的土壤为粉质粘土，样土含水率约为28.7%，站内所用输气管道为X52级钢管。查询相关文献与规范后，管道及土壤的主要物性参数如表1所示。

表1　管道与土壤的主要物性参数

由于岩土类材料与金属材料的塑性变形规律区别较大，土壤应力-应变关系采用Drucker-Prager (DP)模型来反应，表2为其主要参数。

表2　土壤DP模型的主要参数

1.3有限元模型建立

用有限元软件ANSYS模拟站内管线的变形行为，根据现场调查以及燃气输送站内埋地管道的基本情况，本文选取实测时冻胀位移最大的管线区域来建立有限元埋地管道模型，从而模拟其冻胀变形。管道尺寸ø610 mm×9.53 mm，90°弯头拐角处R=1.5D，埋地管线部分长为 2 5000 mm，其中心距地面的埋深为2 050 mm，露天外伸部分管长为2 000 mm，其中心距地面为1 000 mm，所建立土体尺寸45 m×20 m×10 m，有限元网格如图 1所示。

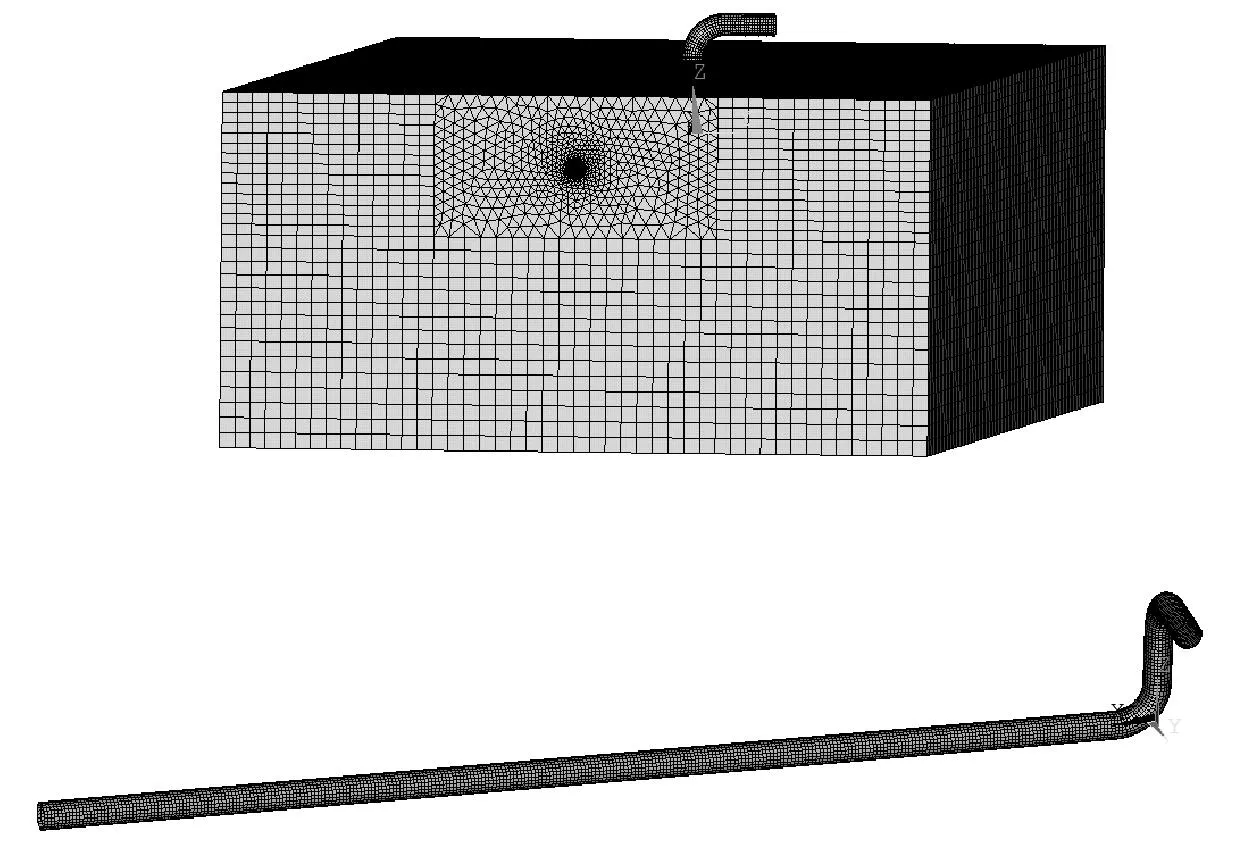
图1　管-土有限元模型的网格划分

1.4载荷与边界条件的确定

根据实测工况所得数据，管内所受压力为1.6 MPa，管道两端横截面所受管内正压所产生的等效端面拉应力为-24.49 MPa，视管道周围回填土为一次性外部载荷施加于管道外表面[4]。依据式(1)M-S理论[5]公式求得埋管上表面所受到的竖直土压为23.627 kPa。

(1)

式中：q为填土表面所受均布载荷，kN/m2；γ为回填土的容重，kN/m3；B为沟槽宽度，m；φ为回填土与沟槽壁之间的摩擦角；c为回填土与沟槽壁之间的粘聚力，kPa；H为埋管最外层距地表的深度，m；K为土压系数，K=tan2(45-φ/2)。

温度载荷的设定：管道内壁温度取实测所得数据中的最低值-7 ℃，埋管与其周围土壤的换热系数为1.5772 W/(m·K)。环境大气温度取冬季时的0 ℃，地表与环境的换热系数为17.82 W/(m·K)，并根据文献[6]知，土壤10 m深处为恒温层，取4.1 ℃。

土体边界约束条件取底面与四周固定约束，并对管道的直线段施加沿轴向的约束。将土体模型尺寸建立的较大些，能够有效地减小土壤边界条件对埋管周围温度场以及应力场的影响，使得模型更切合实际。载荷与约束设置完毕后的有限元模型如图2所示。

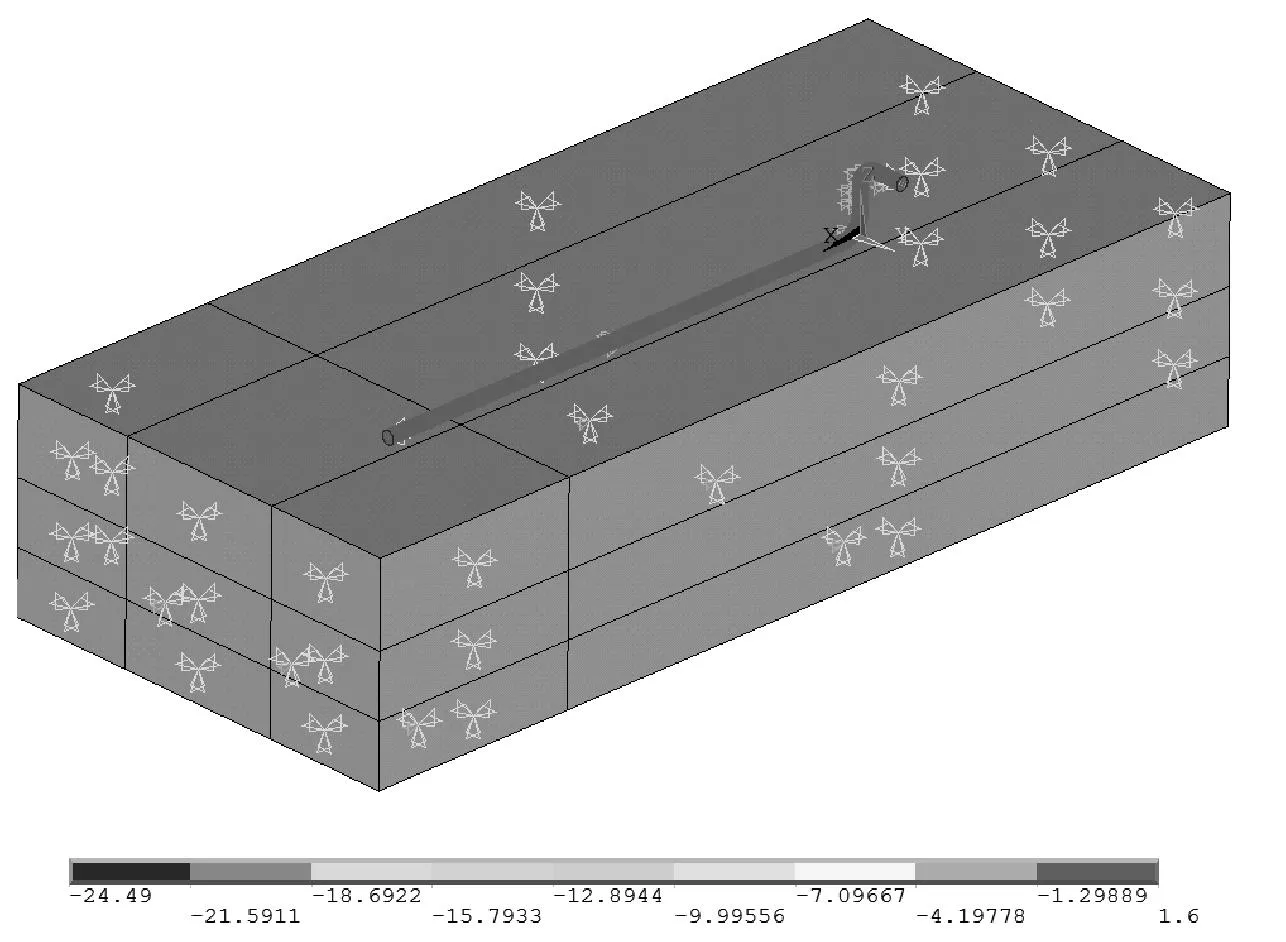
图2　管-土有限元模型的加载与约束示意

2数值模拟结果分析

2.1模拟结果分析

选用Solid90热分析单元对管-土模型进行温度场稳态模拟计算，求解结束之后，将热与结构单元进行转换。土壤冻胀时与埋管之间有接触摩擦作用，伴随着位移与变形量的增加，二者之间的接触力和接触部位不断发生非线性的变化。故令埋管外壁面为刚性目标面，选用Targe170目标单元，土壤为柔性面，选用Conta173接触单元，摩擦因数设为0.4，从而对冻胀时管与土之间的接触进行模拟[7]。图3～6为冻胀作用下埋管的各向位移云图(x为轴向，y为横向，z为竖直方向；总位移为x、y、z3个向的位移矢量和)，图7为管道应力云图。

图3　埋管x方向位移分布

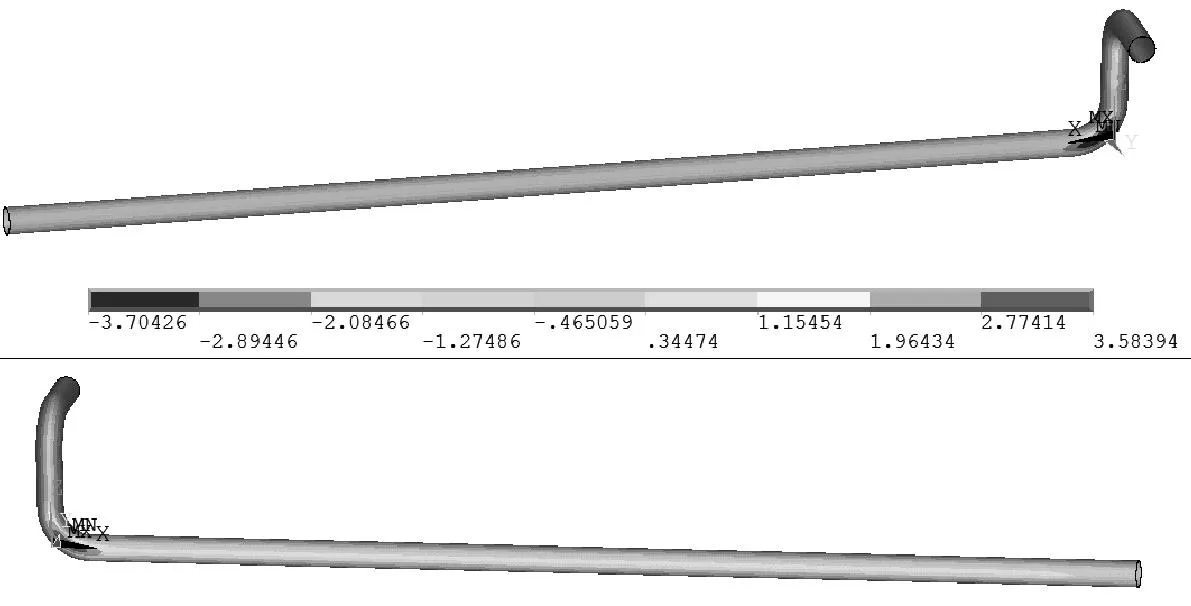
图4　埋管y方向位移分布

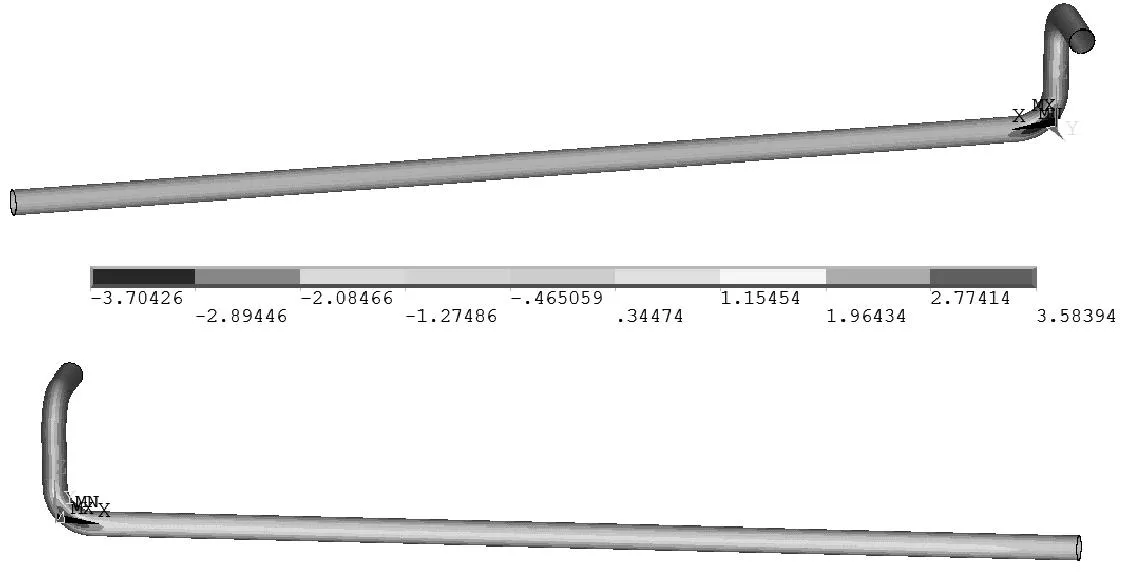
图5　埋管z方向位移分布

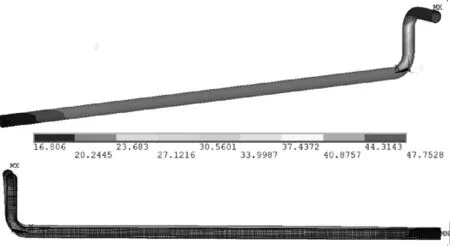
图6　埋管总位移分布

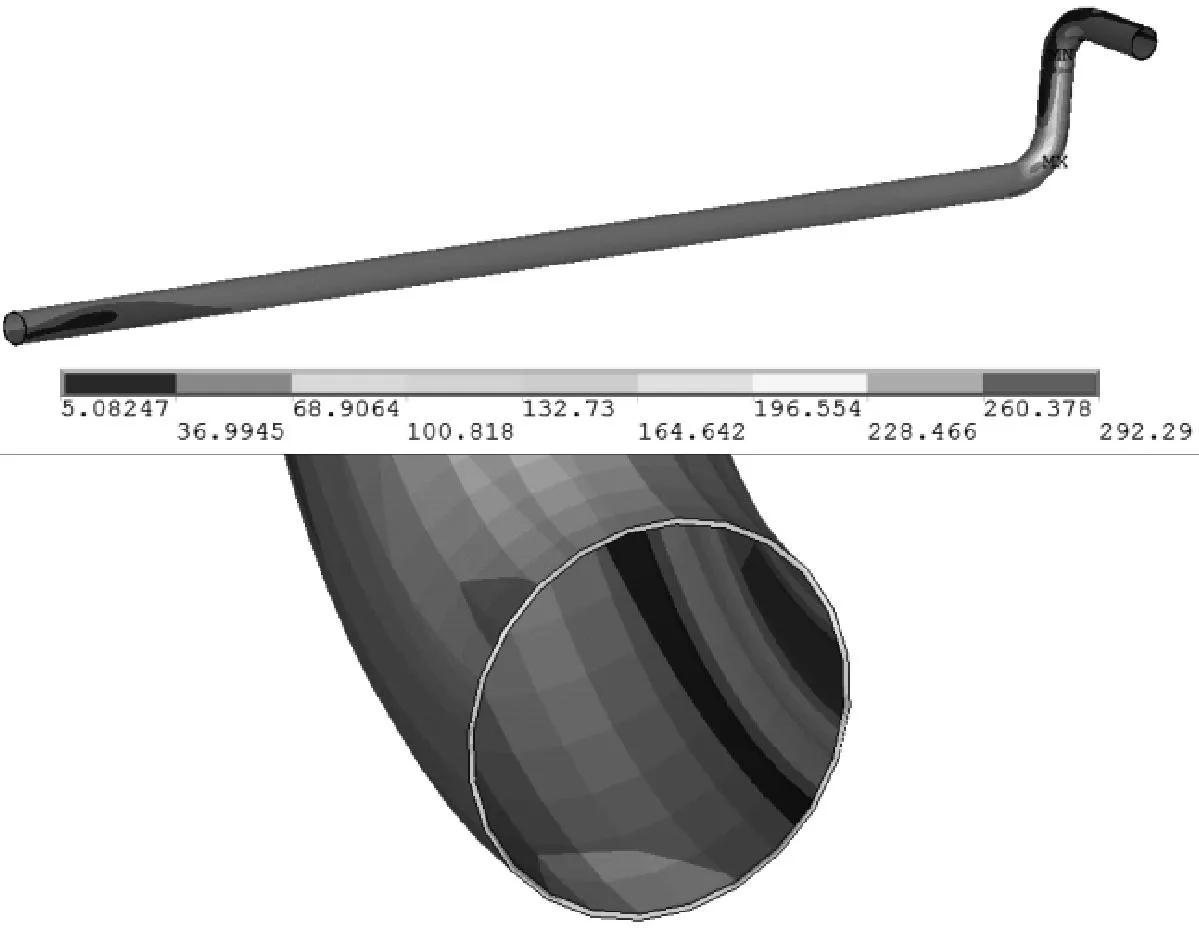
图7　埋管应力剖视图分布

根据图3～6可知，对于埋管的x方向位移，由于埋管的一端受到轴向约束，并且埋管的弯管处与直线段的冻胀变形情况不同，产生了不均匀冻胀，导致埋管直线部分产生向着x轴负向的拉伸力，使得埋管向该方向产生了较大位移量。对于埋管的y向位移，因土体发生冻胀后向上产生冻胀位移，并且以埋管的中心呈对称性分布，所以埋管在沿y轴横向上的位移变化和差异相对于其他2个方向而言要小很多。埋管z轴竖直方向的位移，由于土壤发生冻胀时，冰水相变，体积膨胀，敷设于地下的管道整体都被其抬高，但由于埋管端面的轴向约束，导致了埋地直管段中部管线受冻胀影响竖直位移量最大，这也直接引发了其上方地基表面裂纹的滋生。对于外露的管线所发生位移，其产生原因主要由埋管x和z轴的位移变量共同作用产生。 从图7可知，当忽略冻胀效应对埋管所带来的影响，仅由内压与温度应力所产生的位移量很小。

对于埋地管道，普遍应用第四强度理论对管道进行失效评定(第三理论常应用于露天的管道)。所以对埋管最大应力点进行评定时，应选择Von Mises屈服准则。依据JB4732—1995《钢制压力容器-分析设计标准》中的要求来对最危险区域实施应力的划分与线性化评定。表3即为管道最大应力点的评定结果。

忽略冻胀，即模拟时不考虑土壤的线膨胀系数，从上表可知无论有无冻胀管道的最大应力点都集中于埋管弯头处，这主要是因为埋管自身结构的不连续与在管内压和冻胀的共同作用下，由于埋管上方土壤的抗拔阻力不大和管末端的轴向约束无法完全限固住埋管的变形，导致埋管直线段的位移量朝着弯管处富集，使得埋管弯头处产生比较严重弯曲变形，引起较显著的应力集中现象。其中一次应力以局部薄膜应力为主，并且对比2组数据的一次应力强度可知基本无较大差异，因为该应力主要由平衡管内压力所致，与冻胀与否并无很大关系。二次应力为自限性应力，主要由协调冻胀变形所致，故冻胀效应越显著，二次应力就越大，所以当忽略冻胀影响，一次应力和一次加二次应力在数值上无很大差别。本例中，当燃气管道受内压和冻胀影响发生一定量的变形后，因管内压力不大，管壁又较厚，故不会发生强度破坏，管道仍处于安全状态。但当冻土消融之后，管道可能无法完全复位，多次往复，管线上浮迹象逐渐明显，长此以往易对站点的安全平稳运行埋下隐患，应予以重视。

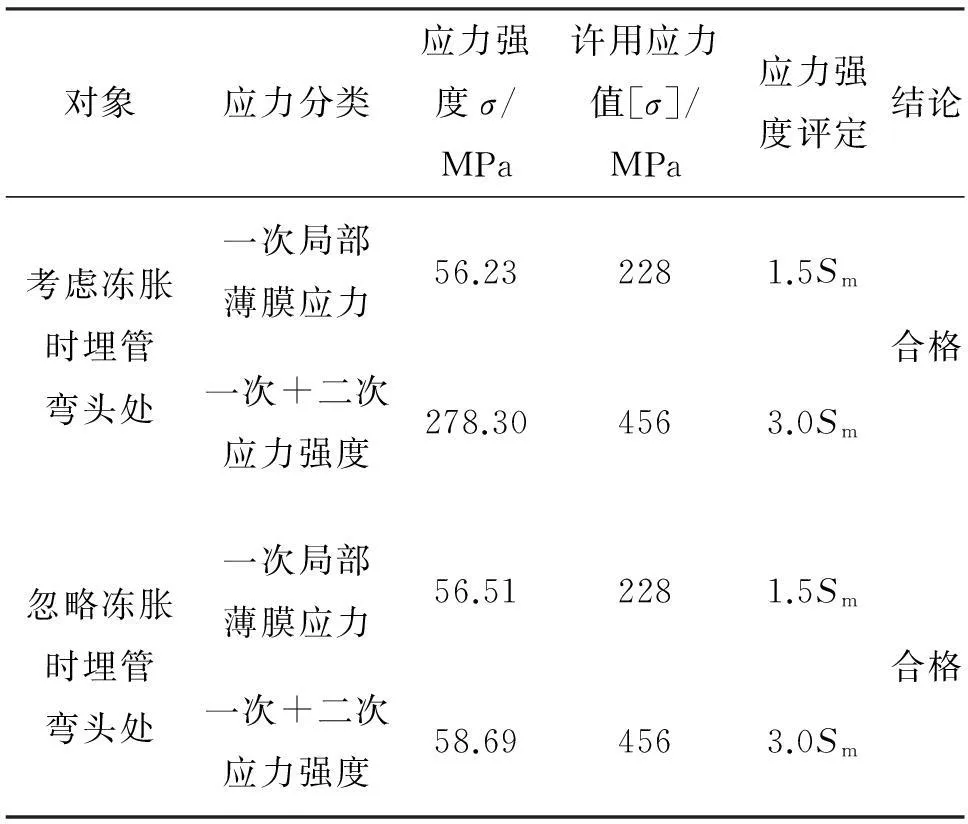
表3　管道危险区域的最大应力点评定结果

2.2模拟结果与实测值比较

为了验证所建模型与模拟方法的合理与正确性，对冻胀影响下埋管的数值模拟结果分别提取对应于实际测量点处的应变值，其示意图如图8所示，并将其逐一进行对比，所绘曲线如图9所示。

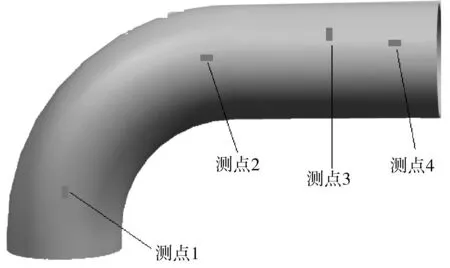
图8　实际测量点所处位置示意

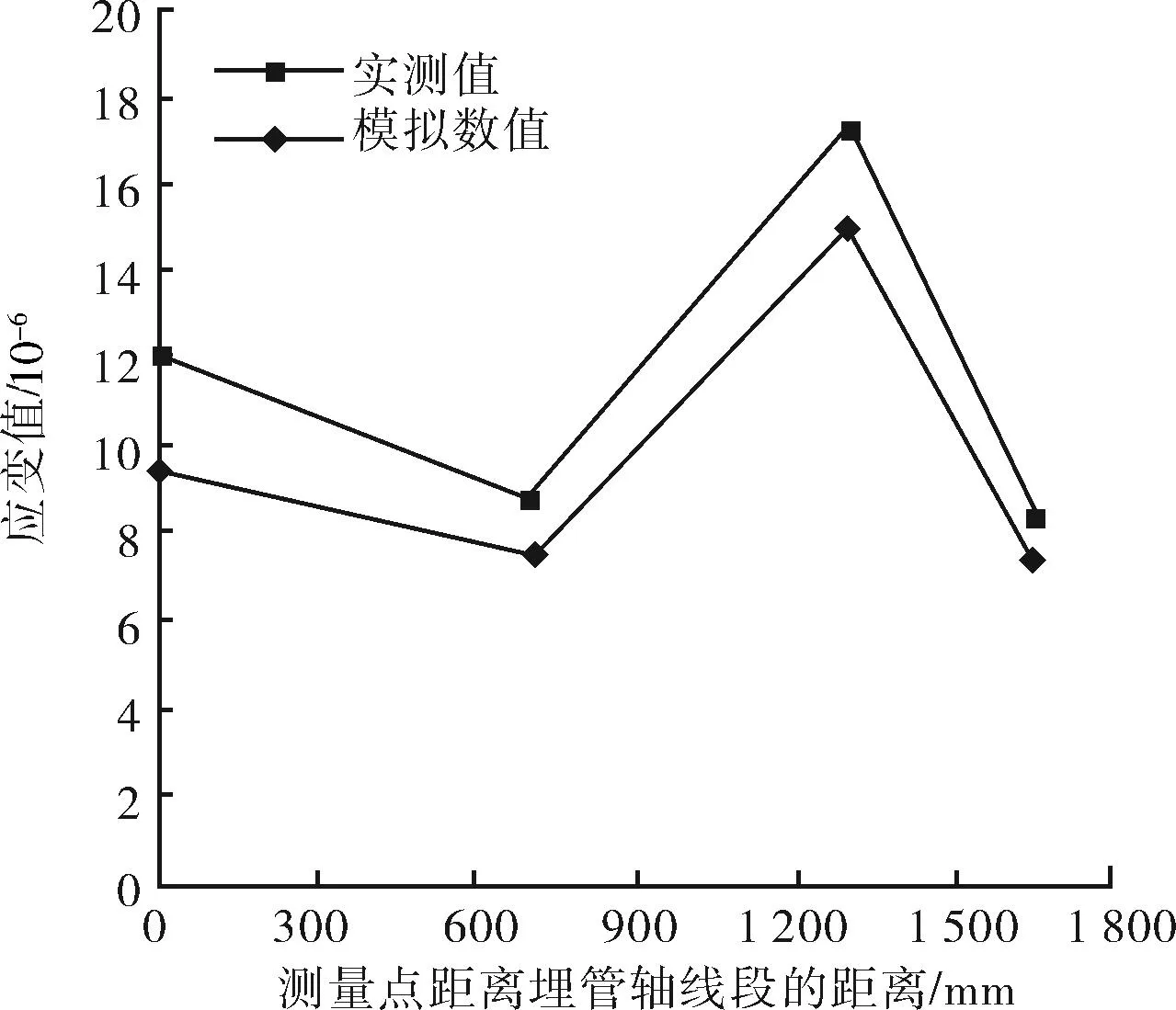
图9　埋管实测应变值和数值模拟结果的对比曲线

根据图9可知，模拟结果均较真实值偏小，其相对误差的算术平均值为14.62%，引起该误差的主要原因为：虽然埋管内的气体温度按照所测得最低温度进行了模拟计算会导致计算结果偏大，但是分析中未考虑水分场的影响即由于水分迁移所导致的分凝冻胀部分；土壤的性质并非一尘不变(尤其是土壤含水率的变化对于冻胀的影响)，此外数值模拟也很难将此前因冻胀融沉所产生的累积性位移量加以考虑，这些因素皆可引起误差的产生致使数值模拟所得结果小于实际测量值。

3分析与讨论

为了具体探究埋管管径、敷设深度、土壤夯实度以及含水率以及保温层对于管道所受土壤冻胀效应的影响，故将对其利用控制变量法进行逐一的对比性分析与讨论。

3.1管径尺寸与埋置深度的影响

根据输送压力值，本例中所使用的埋地燃气管道选用X52钢管，对应于我国的L360系列钢管。将式(2)所得结果圆整，据此数据把不同系列的钢管细分为不同的壁厚等级。

Sch=p/[σ]t×100

(2)

式中：Sch为壁厚等级；p为设计压力，MPa；[σ]t为钢管在该工作温度下的许用应力，MPa。

选取同等壁厚等级下的ø406.4 mm×7.92 mm、ø457 mm×7.92 mm、ø508 mm×9.53 mm、ø559 mm×9.53 mm与ø610 mm×9.53 mm不同管径的钢管，在埋置深度为2.05 m，土体含水率为28.7%，夯实度95%的同种工况下，分析对比管道管径的不同对于其发生冻胀变形的影响。图10～11即为埋地管道各方向位移和最大应力点强度随管径尺寸的变化曲线。此外，基于实际埋深，取其前后不同的管道埋置深度1.6～2.4 m的工况，以管径ø610 mm×9.53 mm为例，在其他工况相同的情况下，分析对比埋置深度的不同对于管道发生冻胀变形的影响。埋地管道各方向位移和最大应力点强度随管道埋置深度变化情况如图12～13所示。

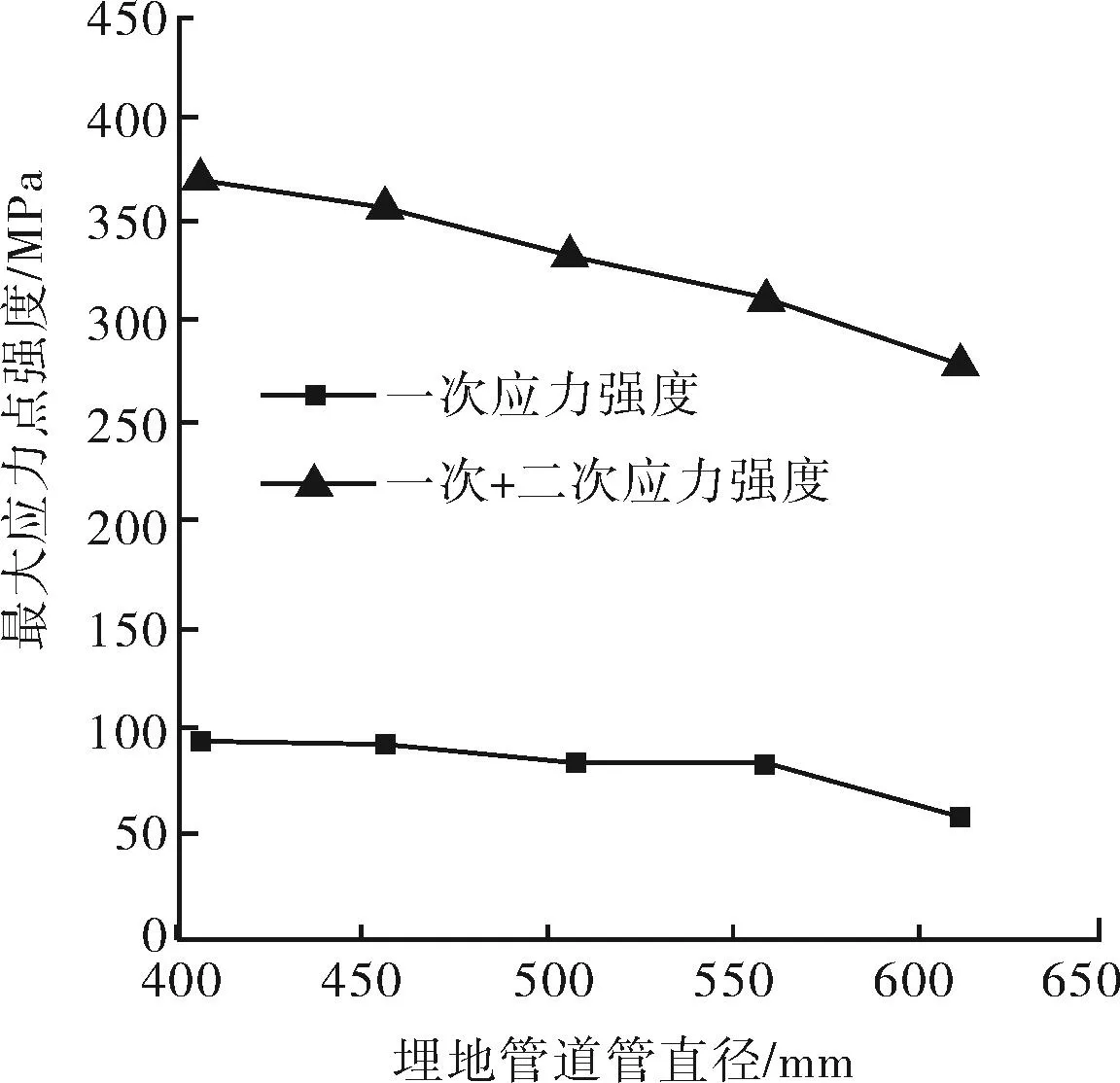
图11　埋地管道最大应力强度随管径尺寸的变化

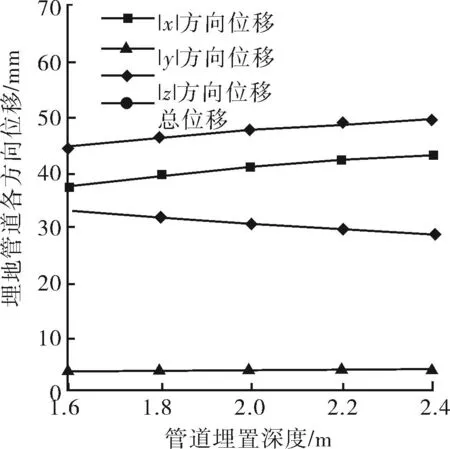
图12　埋地管道各方向位移随埋置深度的变化

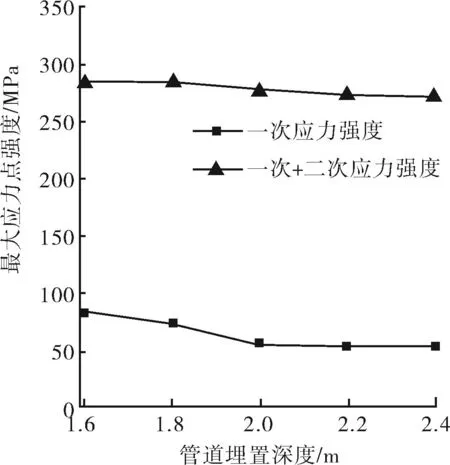
图13　埋地管道最大应力强度随埋置深度的变化

由图10～13可知，管径尺寸和敷设深度都对冻胀效应有一定的影响，尤其是埋管竖直方向的位移变化较为明显。大管径的埋管向其周围土壤所传递的热量较小管径多，导致冻结冰层稍厚，竖直位移量增加。埋管所受土压随着埋深的增大而增大，竖直方向位移随之减小。

埋管最大应力点的一次加二次应力强度之和随着管径的增大和埋深的增加呈衰减趋势，而在一次应力强度方面，管径ø508 mm和ø610 mm处都有较大幅度的降低，究其原因：①因为管径厚度的增加，提高了管道自身的强度与刚度；②由于管径的增大使得弯管处的曲率半径增大，降低了该处的结构不连续性。对于同一管径，随着埋置深度的增加，地表环境温度对于埋管周围的温度场影响随之减小，并且土壤对埋管的约束力(即抗拔阻力)会随之而增大，从而抵消了一部冻胀力作用并且增加了与管道相互之间的变形协调性。可见，在同一壁厚等级下，使用较大管径并且增加敷设深度能较有效地降低埋管所受到的冻胀力，当然还应综合考虑多方面因素如：工艺要求、施工条件、经济成本(建造、运行、维护)等因素，而并非一味地为了减小冻胀效应去改善某些条件。

3.2回填土夯实度与土壤含水率的影响

为了分析回填土夯实度以及土壤含水率对于埋管所受冻胀效应的影响，以管径ø610 mm×9.53 mm为例，在其他工况相同的情况下，分析回填土夯实度从85%～95%的变化和粉质粘土的塑限值(21.2%)与液限值(34.2%)含水率区间内变化对于管道发生冻胀变形的影响。埋地管道各方向位移和最大应力强度随回填土夯实度变化情况如图14～15所示，随含水变化情况如图16～17所示。此外，由于土壤的夯实度，含水率与其冻胀率密切相关，而线膨胀系数又与冻胀率相关，本文按照式(3)和式(4)来确定它们之间的相互关系。

粉质粘土的冻胀系数与这三种因素的三元线性回归方程[8]：

η=β0+β1ω+β2δ+β3|t|

(3)

式中：ω为土壤含水率；δ为夯实度；t为冻结温度。β0、β1、β2、β3为变量系数，分别等于-26.748、0.545、0.171、0.051。

在ANSYS仿真软件中，可将土壤的冻胀率η与其热膨胀系数ε按照式(3)进行关联[9]：

η=ΔT·ε(1+μ)/(1-μ)

(4)

式中：ε为土壤的热膨胀系数，℃-1；ΔT为土壤冻结时所对应的温变值，℃；μ为土壤的泊松比。

注：线膨胀的定义是材料每升高1 ℃时的线伸长量，而对于土体发生冻结时，土壤反向膨胀，故其线膨胀系数应取为负值。

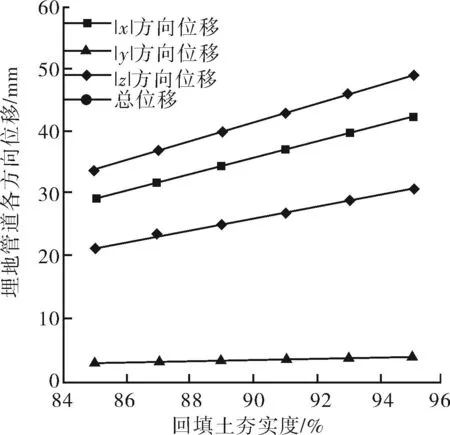
图14　埋地管道各方向位移随土壤夯实度的变化

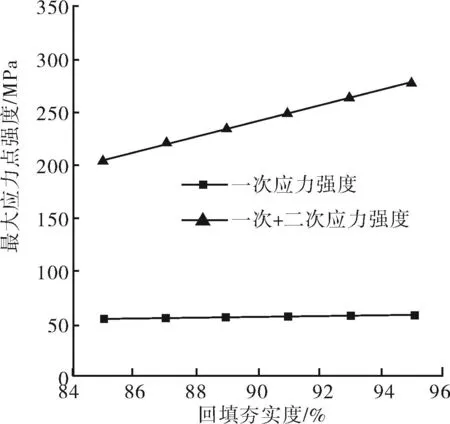
图15　埋地管道最大应力强度随土壤夯实度的变化

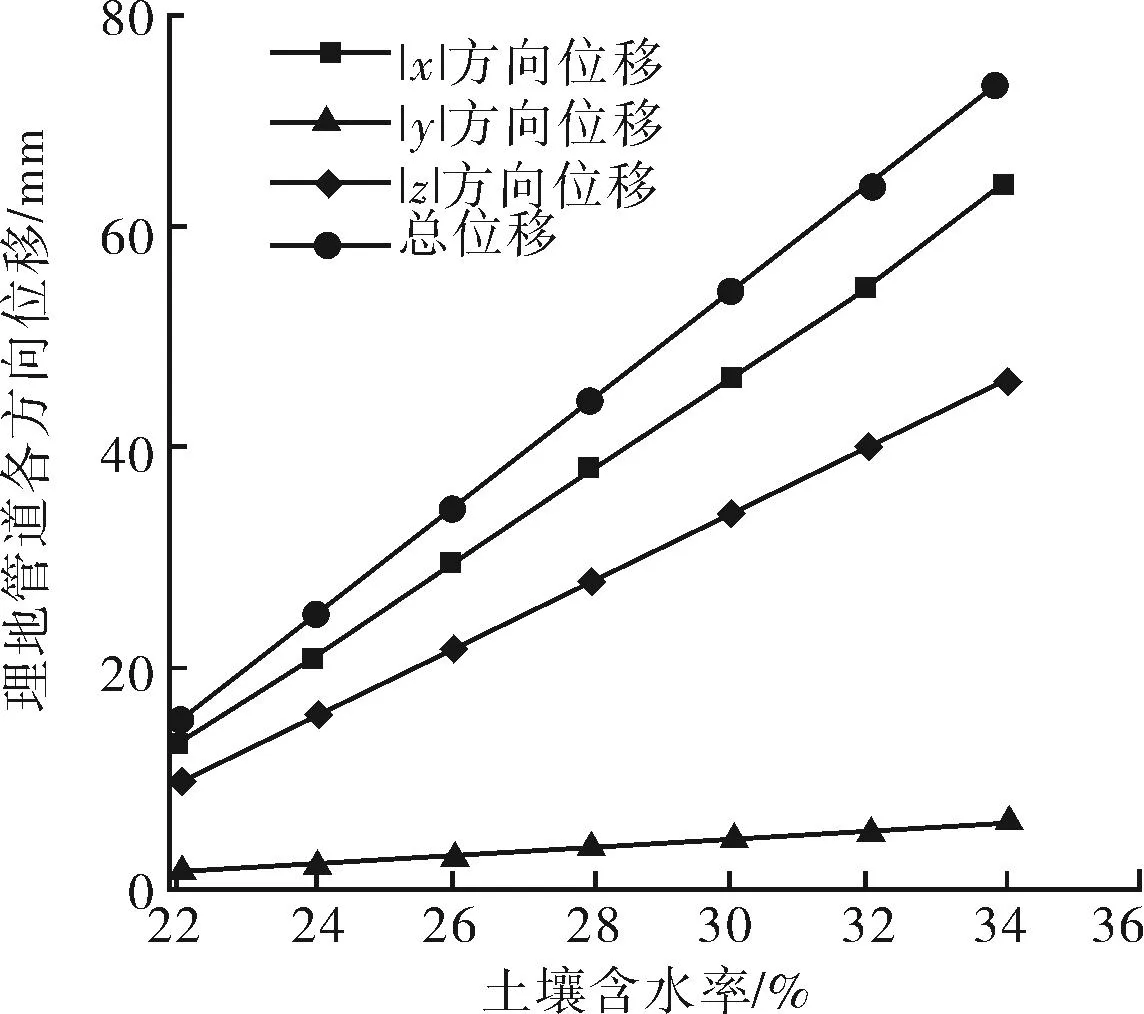
图16　埋地管道各方向位移随土壤含水率的变化

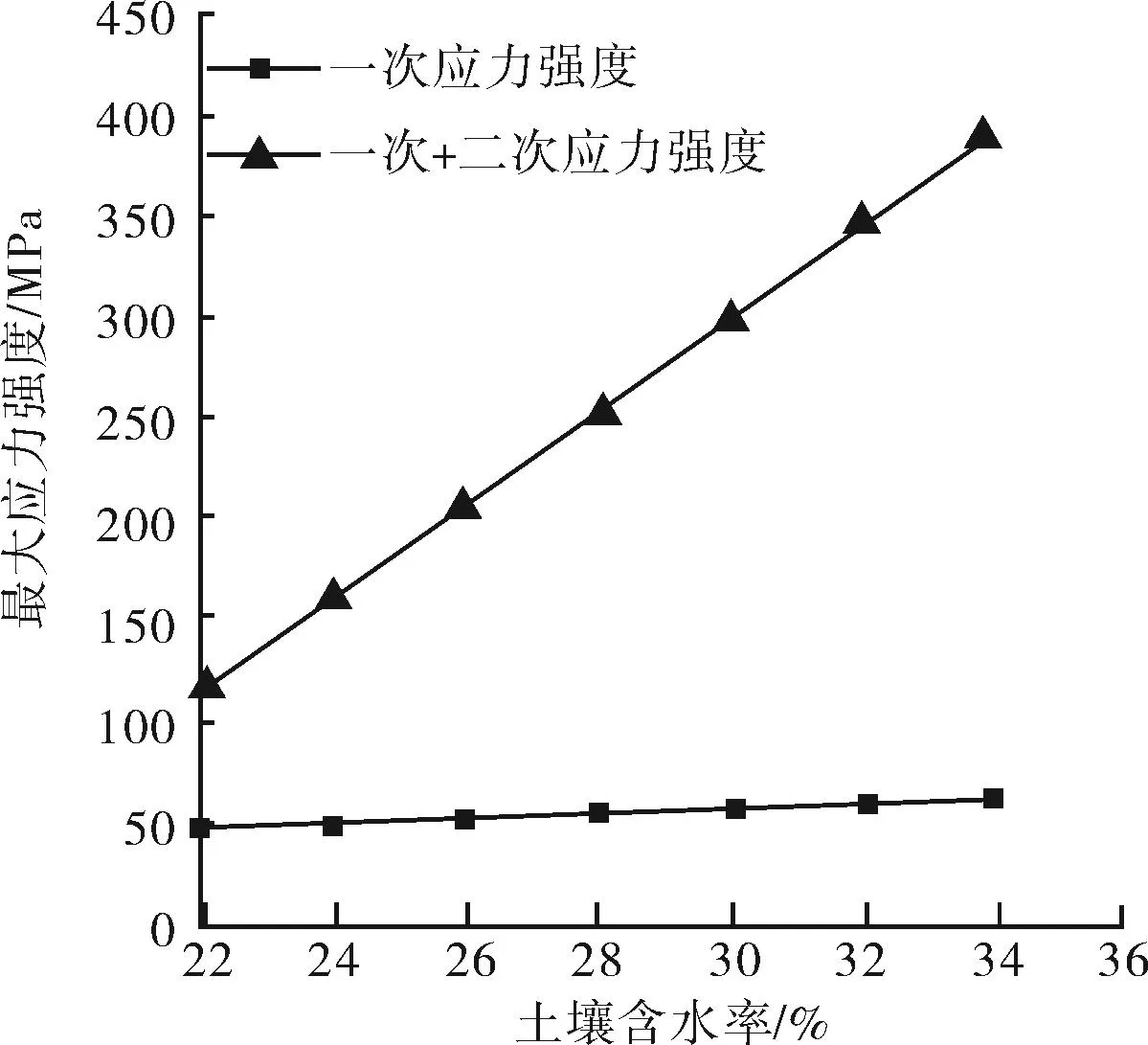
图17　埋地管道最大应力强度随土壤含水率的变化

由图14～17可知，由于夯实度和含水率的变化直接影响冻胀率，所以埋管各方向的位移均呈较明显变化。此外，埋管最大应力点的一次加二次应力强度之和随着夯实度与含水率的增大均呈明显的递增趋势，这是因为伴随着土壤密实度的逐步增加，土壤的饱和度随之增大，那么土壤中水分冻结时所引发的体积变化量无法全部得到释放，致使土壤的冻胀效应显著；当土壤中的含水率愈高时，在其他条件相同的情况下，土壤中会因此产生更多的冰晶体，即具体表现为土壤冻结时冻胀量的增加，冻胀效应的加剧。但对于同一管径，其所受一次应力却变化不大，这是因为其主要和管内压力相关。综上对比各种因素对于埋管所受冻胀的影响可知土壤含水率的变化对其影响最大，故要预防和减小埋管的冻胀作用，应首先控制好埋管周围土壤的含水率，增设必要的防水层，落实好管道与土壤之间的阻水、隔水措施，从而防止严重的冻胀破坏发生。

4结论

1)管道会在弯管不连续处产生应力集中现象，虽然冻胀力作用对埋管一次应力强度的影响并不大，但对其一次与二次应力之和影响较大。因此，应采取相应的预防措施来防止因往复的冻融而导致管线的积累性位移叠加所引发的失效。

2)在大管径下，虽然管道各方向的位移量有所增加，但是其应力状态却随之呈下降趋势；在较大埋置深度时，管道的竖直方向位移量与应力状态均呈下降趋势；在低压实度与含水率工况下，由于土壤冻胀率变小，所引起的冻胀效应相对较小，反之亦然。这对预防和解决埋管冻胀变形问题具有重要的参考价值。

3)土壤冻胀是一个复杂的过程，其物性与力学参数会随着相变及其他参数的改变而改变。本文仅考虑已冻和未冻，且未考虑水分迁移的影响，这必然使得计算结果产生一定的误差。土壤冻融过程中各参数的变化还需要更多的试验研究来测定，为今后的数值模拟提供可靠的理论依据。

参考文献：

[1]孙晖.上海市天然气主干管网系统运行工况分析研究[D].上海：同济大学，2007．

[2]孙明烨，李永威，卢迎九，等.燃气管道上浮的原因与技术处理措施[J].煤气与热力，2007，27(11)：5-7.

[3]熊寅铭，谷英翠，孙伶，等.天然气管道分输站埋地管道冻胀范围预测[J].油气储运，2012(8)：633-635.

[4]龚爱民，傅蜀燕，黄海燕.ANSYS软件在分析地下埋管工程中的应用[J].安徽建筑工业学院学报：自然科学版，2004，12(5)：51-55．

[5]陈仲颐.土力学[M].北京：清华大学出版社，1994：234-235.

[6]Liu Xiaoyan，Zhao Jun，Shi Cheng，et a1.Study on soil layer of constant temperature[J].Acta Energiae Solaris Sinica，2007，28(5)：494-498.

[7]王勇，吴亚平，郭春香，等.多年冻土区埋地输油管道的应力及变形分析[J].兰州交通大学学报，2008(27)：44-46.

[8]程培峰，尹传军.季冻区粉质黏土冻胀特性分析[J].公路交通科技，2014，31(1)：44-49.

[9]洪帅.季节冻土区路基土体的冻胀率与热膨胀系数关系分析[J].科技致富向导，2013(16) ：230-231.

[10]王鹏，王峰会.内压和侧压作用下管道的屈曲分析[J].石油矿场机械，2008，37(8) ：18-19.

Numerical Analysis of Deformation of Buried Pipeline in Gas Station

SU Wenxian1，DENG Lei1，LI Xu1，WU Xiaomin2

(1．SchoolofEnergyandPowerEngineering，UniversityofShanghaiforScienceandTechnology，Shanghai200093，China；2.ShanghaiNaturalGasPipelineNetworkCompanyLtd.，Shanghai201204，China)

Abstract：Simplifying the model of the tube-soil frost heave，considering the non-linear contact between tube and soil based on the soil’s characteristics，coupled thermo-mechanical analysis for the influence of frost heaving to buried pipes in gas station were completed by using the ANSYS software.After that，stress intensity is checked to compare the result with the measured data，it is indicated that the simulation method is feasible. By using the methodofcontrolvariables， stress distribution and displacement of buried pipes in different diameter，buried depth，compaction degree of backfill and soil moisture content are analyzed and discussed.It is found that the soil moisture content has greater influence on the effect of frost heaving to buried pipes.

Keywords：buried pipeline；deformation；numerical simulation

中图分类号：TE973

文献标识码：A

doi：10.3969/j.issn.1001-3482.2016.02.013

作者简介：苏文献(1967-)，男，山东烟台人，副教授，博士，研究领域：过程设备数值仿真。

收稿日期：①2015-08-06

文章编号：1001-3482(2016)02-0057-07