行波反射法在变压器绕组匝间短路故障定位中的应用

李卓昕，彭敏放，黄清秀，万 勋,2，刘 达

行波反射法在变压器绕组匝间短路故障定位中的应用

李卓昕1，彭敏放1，黄清秀1，万 勋1,2，刘 达1

(1.湖南大学电气与信息工程学院，湖南 长沙 410082；2.国网湖南省电力公司电力科学研究院，湖南 长沙410007)

针对变压器绕组轻微匝间短路难以检测的问题，提出利用行波反射波的电压幅值进行匝间短路故障定位的方法。通过在变压器绕组线端输入单个低压脉冲以获取行波反射信号，从采集到的行波反射信号中提取相应的波峰电压幅值，以此作为故障诊断的电气量。根据匝间短路后对应匝波阻抗改变引起的反射电压突变，来实现匝间短路故障定位。仿真结果表明所提方法简单可行。

变压器；行波反射法；波阻抗；匝间短路；故障定位

0 引言

绕组匝间短路故障是电力变压器主要的内部故障形式，随着电压等级的提高，变压器发生匝间短路的概率将越来越大。较为轻微的绕组匝间故障不会对变压器运行产生严重影响，但它是变压器绕组绝缘劣化的先兆和表现形式，将引起绝缘的进一步恶化，导致变压器绕组严重烧损[1-2]。因此及时发现绕组早期轻微匝间绝缘故障，并正确地定位出故障点在绕组线圈的位置，对研究和探索变压器保护新原理和变压器的检修维护将具有十分重要的意义。

在常见的变压器绕组内部故障诊断方法中，变压器油中溶解气体分析(DGA)[3]和局部放电检测技术[4]能有效发现变压器内部的潜伏性故障及其发展程度，并在匝间短路故障的定性诊断方面取得了效大的成功，然而对于轻微匝间短路故障的及时诊断与定位还需进一步的研究。

近年来随着输电线路上故障行波定位技术和行波选线技术[5]的成功应用，国内外掀起了对暂态故障行波信息的研究热潮，行波定位技术也被成功地应用到发电机绕组匝间短路故障定位中[6]。本文将行波反射法引入变压器绕组匝间短路故障中进行定位研究。首先分析了行波在变压器绕组上的传播特性，根据传播特性建立了基于变压器绕组多导体传输线(MTL)理论[7]的Matlab仿真模型。在绕组线端输入低压脉冲以获取行波反射信号，从采集到的行波反射信号中提取相应的波峰电压幅值，以此作为故障诊断的电气量。通过分析绕组不同位置发生匝间短路时，故障行波反射曲线与正常行波反射曲线对应匝电压幅值的突变，来实现故障诊断与定位。仿真实验结果证明本文方法是可行的。

1 行波在变压器绕组上的传播特性分析

1.1 行波的折射与反射

由行波的传播特性可知：当行波经过传输路径中的阻抗不连续点时，会在节点处发生折射与反射。如图1所示，电压波U1q到达节点A时，由于波阻抗不连续两侧波阻抗分别为Z1和Z2，而得到反射波U1f和折射波U2q。Ku为电压反射系数，由行波折反射性质可得

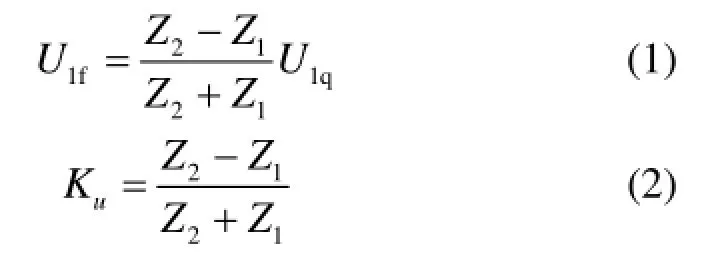
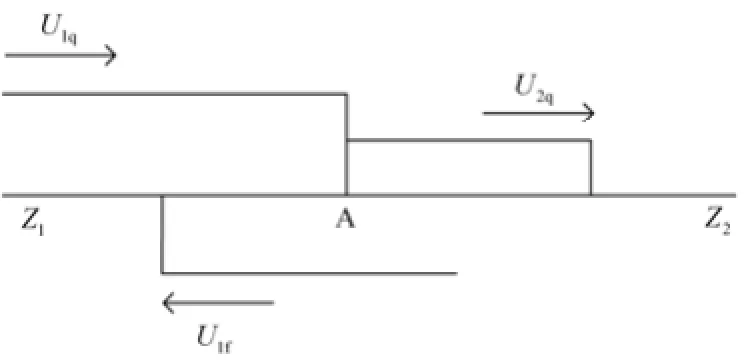
图 1 行波的折射与反射Fig. 1 Refraction and reflection of traveling wave

1.2 行波在变压器绕组上的传播

变压器绕组形式主要有层式、饼式和交错式。在大中型变压器中应用最广的绕组形式是饼式绕组，其特点是沿轴向高度绕组由一个个水平的、与油道垂直的线饼所组成。由于变压器线圈线匝长度远大于邻近线匝之间的距离，电磁边界在线匝换位处不连续，相邻线匝换位处波阻抗有比较明显的变化[8]，所以可以把变压器绕组的每一匝近似看成一根均匀传输线，把行波反射法应用到变压器绕组匝间短路故障定位研究中。

图2为一个m匝绕组线圈展开示意图，当向变压器绕组线端注入合适的脉冲信号U1q时，由于相邻匝连接处存在明显的波阻抗变化，所以注入脉冲每经过一个匝连接点都会发生一次折射与反射，折射波作为下一匝的输入波继续沿导线传播，而反射波则作为对应匝的特征波返回输入端。如第n匝绕组Zn处产生折射波U(n+1)q继续向下传播，而反射波Unf则往注入点回传再经过 n-1匝回到注入点，端口处的Unfnq就是对应的第n匝的反射特征波[9]。经过上述分析，行波在变压器绕组上传播，每经过一匝都会在匝与匝的交接处产生一个对应的反射波回到注入点，随着绕组匝数的增加，折反射次数增多，对应波形也会有所改变。因此理论上在对变压器绕组注入合适的脉冲信号时，会在注入端采集到一连串相邻的波形相似的反射波，依次对应变压器的每一匝绕组。

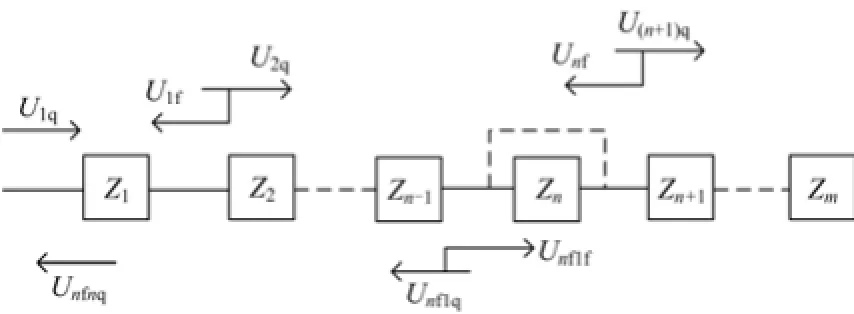
图2 行波在绕组中传播过程示意图Fig. 2 Dissemination process schematic of the travelling wave in windings

1.3 匝间短路时的反射波变化

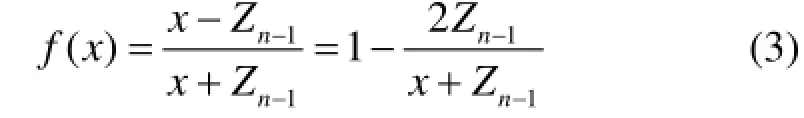
显然f(x)为增函数，进而推出f(Zn)＜f(Zn+1)，即

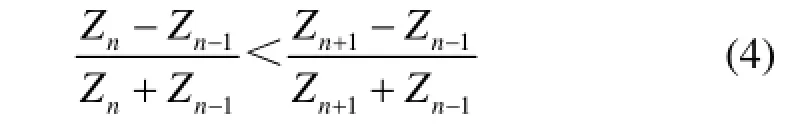
所以匝间短路后对应匝的电压反射系数增大。根据式(1)对应短路匝的反射电压幅值也会相对正常时对应匝的反射电压幅值增大，而n匝之前的线匝反射波电压基本不受影响。因此可以根据匝间短路后对应匝的反射电压突变来实现故障定位。

2 变压器绕组匝间短路的定位分析

根据上述分析，在对变压器绕组注入合适的脉冲信号时，若变压器绕组存在匝间短路，则匝间波阻抗变化量增大，导致电压反射系数Ku增大，从而引起对应匝的反射电压幅值变大。那么通过对比无故障时的绕组行波反射曲线，首次出现反射波电压相对正常时突变的即为发生了匝间短路，反射波对应的绕组匝即为故障匝。

综上，可采用如下方法确定变压器绕组匝间短路位置，具体步骤如下：

1) 在变压器绕组端口输入合适的单个低压脉冲，在输入端得到绕组的行波反射曲线；

2) 结合行波反射曲线与相应的电压数据，提取每一匝对应的反射波最大电压幅值并记录下来，如第n匝的最大反射波电压记录为Un。对于m匝的变压器绕组就会得到m个电压数据，并记为特征向量X为

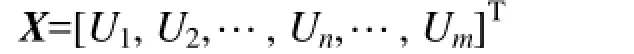
3) 将得到的特征向量X中的每一项电压Un与正常时的特征向量的每一项电压作商得f(n)为

若计算得f(n)大于常数T，且n属于1到m中最小即首次出现，则n即为匝间短路故障匝。理论上T取1即可，但考虑到反射波形存在畸变，根据大量的实验仿真数据，当T取1.15时既能准确判断故障，又能躲过因为波形畸变造成匝间短路误判。即n=minY，Y {1,∈ 2,L, m}且f(n)>1.15，那么n就为匝间短路故障匝。

由于当变压器靠近输入端口的绕组发生匝间短路时，对应行波反射电压相对无故障时的电压增量特别明显，则可直接从行波反射曲线判断匝间短路故障并得出故障所在匝。

3 仿真验证

3.1 基于MTL的匝间短路仿真模型

大中型变压器中应用最广的绕组形式是饼式绕组，其特点是沿轴向高度绕组由一个个水平的线饼所组成。由于电磁边界在线匝换位处不连续，且绕组每匝的长度远大于邻近线匝之间的距离，所以可以把变压器绕组线圈的每一匝近似看成一根传输线，建立其多导体传输线模型[10]。而前人的众多研究成果也表明了此模型的正确性和实用性。

以匝为单元建立变压器的多导体传输线模型，整个绕组被模拟成多根相互耦合并且首尾相连的多导体传输线。US(i)、IS(i)、UR(i)和IR(i)分别表示第i匝绕组的首端电压，电流向量，末端电压和电流向量。多导体传输线的频域方程为

目前基于变压器MTL模型的仿真多由软件编程实现，但利用编程实现绕组不同位置的匝间短路故障仿真十分复杂，所以本文利用Matlab/Simulink里的Distributed Parameter Line模块[13]搭建变压器绕组MTL模型。如图3所示，利用Simulink搭建了一个40匝的变压器绕组模型，在此模型中可直接用导线短接相邻匝来模拟绕组匝间短路故障。

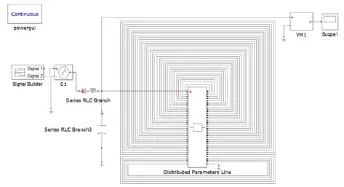
图3 40匝变压器绕组仿真模型Fig. 3 40-turn transformer winding simulation model

3.2 仿真验证

向变压器绕组一端注入一个尖峰电压脉冲，令注入信号的电压幅值为5 V，脉冲时间为10 ns，其中上升沿占整个脉宽的10%。仿真可得无匝间短路时绕组的行波反射曲线，取前10匝对应的反射波形如图4所示，10个明显的最大波峰电压值分别对应1到10匝绕组的反射波最大电压幅值。通过仿真实验数据可得特征向量X为

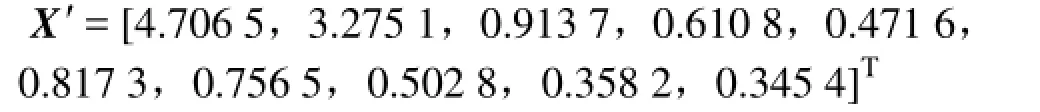
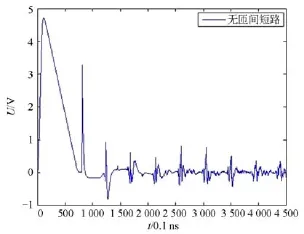
图4 无匝间短路的10匝反射曲线Fig. 4 Reflection curves of the 10th non-short circuited turns

3.3 短路故障匝定位

当第一匝与第二匝绕组发生匝间短路即第2匝被短路时，通过仿真实验可得故障的行波反射曲线如图5所示。

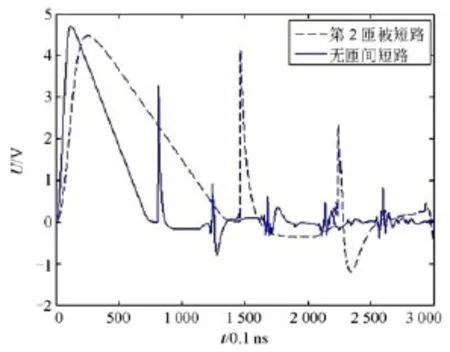
图5 第2匝短路的反射曲线Fig. 5 Reflection curve of the 2th short circuited turns

由图5可明显看到第2匝被短路时行波反射曲线的第二个波峰电压U2相比无故障时的U2有一个突变电压幅值增大。根据式(5)可得 f(2)=U2/U2= 4.137 5/3.275 1=1.26>1.15，可判断第2匝发生匝间短路故障。第3匝、4匝与10匝分别被短路时的仿真实验如图6~图8所示。

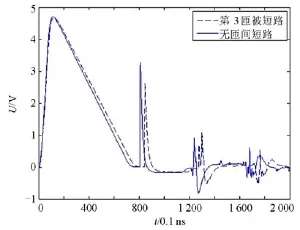
图6 第3匝短路的反射曲线Fig. 6 Reflection curve of the 3th short circuited turns

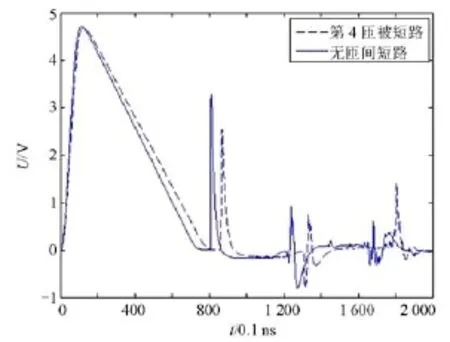
图7 第4匝短路的反射曲线Fig. 7 Reflection curve of the 4th short circuited turns

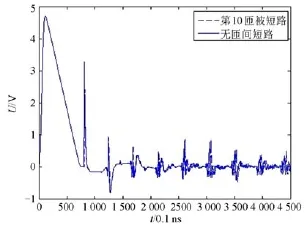
图8 第10匝短路的反射曲线Fig. 8 Reflection curve of the 10th short circuited turns

X=[4.706 5, 3.278 5, 0.898 6, 0.599 2, 0.435 6, 0.851 5, 0.813 2, 0.528 9, 0.382 4, 0.500 1]T

根据式(5)，将X中的电压幅值分别与X＇中对应的电压幅值分别作商可得表1。

由表1可得f(10)=1.448>1.15，且属于首次出现，即可判断为第10匝发生匝间短路故障。

当第20匝发生匝间短路故障时，通过仿真数据分析，前10匝数据与前面类似，取第10匝到第20匝对应的电压幅值与正常时对应的电压幅值，根据式(5)分别作商可得表2。

由表 2可得 f(19)=1.645>1.15，且属于首次出现，即可判断为第19匝发生匝间短路故障。然而实验中是第20匝发生故障，仿真结果表明，随着传输距离的增加，距离入射端越远的绕组匝间短路(特别是二分之一绕组之后的部分)，故障定位准确率越低。可将脉冲输入端口改为绕组末端，将原本的最后一匝看成是首匝重新进行脉冲试验，以提高故障诊断的准确率。

表1 电压幅值比Table 1 Voltage amplitude ratio

表2 电压幅值比Table 2 Voltage amplitude ratio

4 结论

本文通过分析行波在变压器绕组上的传播特性，结合变压器绕组的多导体传输线MTL模型，提出利用在绕组线端采集到的反射行波电压幅值突变来实现变压器匝间短路故障定位的方法。结论如下：

1) 变压器绕组发生匝间短路故障，对应匝波阻抗变化量增大，导致电压反射系数增大，相应的反射波电压幅值增大。当绕组匝的电压幅值比首次出现大于1.15时，反射波对应的绕组匝即为故障匝。

2) 通过故障模拟，仿真分析结果说明了本文提出的故障定位方法在理论上是可行的。该方法适用于大多数的饼式绕组变压器，并且只需从变压器绕组端口采集行波反射信号，通过提取电压数据进行对比分析即可完成判断。

随着变压器绕组匝数的增多，对应的反射波也会不断的衰减和畸变，对于衰减和畸变的反射波如何有效地提取故障特征量进行故障定位将成为本文下一阶段的研究目标。

[1] 程养春, 魏金清, 李成榕, 等. 局部放电作用下变压器匝间油纸绝缘加速劣化规律[J]. 电工技术学报, 2015, 30(18): 203-212.

CHENG Yangchun, WEI Jinqing, LI Chengrong, et al. Development rules of accelerated degradation of oilpaper insulation between turns in transformer windings induced by partial discharge[J]. Transactions of China Electrotechnical Society, 2015, 30(18): 203-212.

[2] 杨理才, 孙结中, 刘蔚, 等. 变压器匝间短路建模及其实际应用[J]. 电力系统保护与控制, 2014, 42(8): 140-145.

YANG Licai, SUN Jiezhong, LIU Wei, et al. Transformer inter-turn short circuit modeling and its application[J]. Power System Protection and Control, 2014, 42(8): 140-145.

[3] 张卫华, 苑津莎, 王杉, 等. 基于改良三比值法的变压器故障基本信度分配计算方法[J]. 电力系统保护与控制, 2015, 43(7): 115-121.

ZHANG Weihua, YUAN Jinsha, WANG Shan, et al. A calculation method for transformer fault basic probability assignment based on improved three-radio method[J]. Power System Protection and Control, 2015, 43(7): 115-121.

[4] 郑书生, 陈金祥, 李成榕, 等. 变压器绕组对局部放电特高频定位方法的影响[J]. 高电压技术, 2013, 39(2): 324-329.

ZHENG Shusheng, CHEN Jinxiang, LI Chengrong, et al. Influence of windings on locating partial discharge in transformers by using ultra-high frequency method[J]. High Voltage Engineering, 2013, 39(2): 324-329.

[5] 何军娜, 陈剑云, 艾颖梅, 等. 电力系统行波测距方法及其发展[J]. 电力系统保护与控制, 2014, 42(24): 148-154.

HE Junna, CHEN Jianyun, AI Yingmei, et al. Fault location methods based on traveling wave theory for power system and its development[J]. Power System Protection and Control, 2014, 42(24): 148-154.

[6] 贾志东, 陈海, 张征平, 等. 采用重复脉冲法诊断发电机转子绕组匝间短路故障[J]. 高电压技术, 2012, 38(11): 2927-2933.

JIA Zhidong, CHEN Hai, ZHANG Zhengping, et al. Inter-turn short faults diagnosis on rotor windings of generator using repetitive surge oscilloscope[J]. High Voltage Engineering, 2012, 38(11): 2927-2933.

[7] 梁贵书, 朱晓燕, 董华英. 高频下变压器绕组的仿真建模[J]. 高电压技术, 2009, 35(2): 393-398.

LIANG Guishu, ZHU Xiaoyan, DONG Huaying. Simulation modeling of transformer windings at high frequencies[J]. High Voltage Engineering, 2009, 35(2): 393-398.

[8] 刘云鹏, 律方成, 李成榕, 等. 基于多导体传输线模型的单相变压器绕组中放电的距离函数法定位[J]. 电工技术学报, 2006, 21(1): 115-120.

LIU Yunpeng, LÜ Fangcheng, LI Chengrong, et al. Distance function locating partial discharge in single phase transformer winding based on MTL model[J]. Transactions of China Electrotechnical Society, 2006, 21(1): 115-120.

[9] 刘达, 彭敏放, 万勋, 等. 基于行波分析的变压器绕组匝间短路故障定位[J]. 仪器仪表学报, 2015, 36(9): 2091-2096.

LIU Da, PENG Minfang, WAN Xun, et al. Inter-turn short-circuit fault location for transformer winding based on traveling wave analysis[J]. Chinese Journal of Scientific Instrument, 2015, 36(9): 2091-2096.

[10] 王赞基, 杨钰. 大型电力变压器线圈中特快速暂态电压分布的计算[J]. 高电压技术, 2010, 36(4): 918-925.

WANG Zanji, YANG Yu. Calculation of very fast transient over voltage distributions in large power transformer windings[J]. High Voltage Engineering, 2010, 36(4): 918-925.

[11] 邓祥力, 高亮, 刘建峰, 等. 特高压变压器模型漏感参数的稳态识别方法[J]. 电工技术学报, 2014, 29(5): 254-260.

DENG Xiangli, GAO Liang, LIU Jianfeng, et al. Steady-state parameter identification of UHV transformer model[J]. Transactions of China Electrotechnical Society, 2014, 29(5): 254-260.

[12] HETTIWATTE S N, CROSSLEY P A, WANG Z D, et al. Simulation of a transformer winding for partial discharge propagation studies[C] // IEEE Power Engineering Society Winter Meeting, 2002: 1394-1399.

[13] 姚致清, 于飞, 赵倩, 等. 基于模块化多电平换流器的大型光伏并网系统仿真研究[J]. 中国电机工程学报, 2013, 33(36): 27-33.

YAO Zhiqing, YU Fei, ZHAO Qian, et al. Simulation research on large-scale PV grid-connected systems based on MMC[J]. Proceedings of the CSEE, 2013, 33(36): 27-33.

(编辑 周金梅)

Application of the traveling-wave reflection method in inter-turn short fault location for transformer

LI Zhuoxin1, PENG Minfang1, HUANG Qingxiu1, WAN Xun1,2, LIU Da1
(1. College of Electrical and Information Engineering, Hunan University, Changsha 410082, China; 2. State Grid Hunan Electric Power Corporation Research Institute, Changsha 410007, China)

Aiming at the problem that the transformer winding is difficult to detect the fault of the inter-turn short circuit, the method of using the voltage amplitude of the traveling wave reflected wave to locate the fault location is proposed. It inputs a low voltage pulse into winding wire end to obtain the traveling wave reflection signal and extracts the traveling wave reflected signal from the peak voltage amplitude, which is used as the electric quantity of the fault diagnosis. According to the change of the reflected voltage caused by the turn to turn short circuit, the fault location of the inter-turn short circuit fault is realized. The simulation result shows that the proposed method is simple and feasible. This work is supported by National Natural Science Foundation of China (No. 61173108 and No. 61472128) and Natural Science Foundation of Hunan Province (No. 14JJ2150).

transformer; traveling wave reflection method; wave impedance; inter-turn short circuit; fault location

2015-10-30；

2015-12-03

李卓昕(1991-)，男，通信作者，硕士研究生，研究方向为电气设备状态监测与故障诊断；E-mail: lizhuoxin1125@ 163.com

彭敏放(1964-)，女，博士，教授，研究方向为电气设备状态监测与故障诊断，智能配电网等；E-mail: pengminfang@hun.edu.cn

黄清秀(1975-)，女，博士，副教授，研究方向为信号处理及电路设计。E-mail: celeron300@netease.com

10.7667/PSPC151917

国家自然科学基金项目(61173108；61472128)湖南省自然科学基金重点项目(14JJ2150)