汽车起重机动力学分析与吊运回转策略寻优

Dynamic analysis of truck crane and optimization of swing rotary strategy

朱长建1，姜洪喆2，王　伟2，陶　永3，郑佳奇3

（1.徐州重型机械有限公司，徐州 221004；2.中国农业大学 工学院，北京 100083；3.北京航空航天大学，北京 100091）

ZHU Chang-jian1,　JIANG Hong-zhe2,　WANG Wei2,　TAO Yong3,　ZHENG Jia-qi3



汽车起重机动力学分析与吊运回转策略寻优

Dynamic analysis of truck crane and optimization of swing rotary strategy

朱长建1，姜洪喆2，王伟2，陶永3，郑佳奇3

（1.徐州重型机械有限公司，徐州 221004；2.中国农业大学 工学院，北京 100083；3.北京航空航天大学，北京 100091）

ZHU Chang-jian1,JIANG Hong-zhe2,WANG Wei2,TAO Yong3,ZHENG Jia-qi3

摘要：以汽车起重机为研究对象，以吊运回转策略寻优为目标建立汽车起重机动力学模型。利用两方向摆角实测数据与模型Simulink仿真结果进行比对，印证理论分析模型的正确性。基于所建立动力学模型，以实测数据拟合为基础，针对不同的吊运回转曲线策略（等加速曲线、三角函数S曲线，以及五次多项式拟合曲线）进行横向比对分析，并对S曲线和五次多项式进行四阶-五阶Runge-Kutta法插值计算，研究结果表明采用五次多项式的吊运回转策略可使回转吊运过程吊重摆角达到最小。

关键词：汽车起重机；动力学模型；Simulink仿真；摆角；回转曲线

0　引言

1　汽车起重机的动力学模型

汽车起重机的实际运动系统是比较复杂的，除了存在机械和动力元件的非线性外，还存在干摩擦、风力阻尼等因素的影响，为了分析其本质，我们忽略些次要因素[7]，将汽车起重机的工作模型（图1）进行简化分析其简化模型。汽车起重机以回转中心做原点，x、y、z坐标简化结构示意如图2所示，定义顺时针旋转为正，以起重机正方向即车头方向为x正方向，起重机左手侧为y轴正方向，以上车的转盘回转中心到臂头点的连线代替主臂作计算依据。

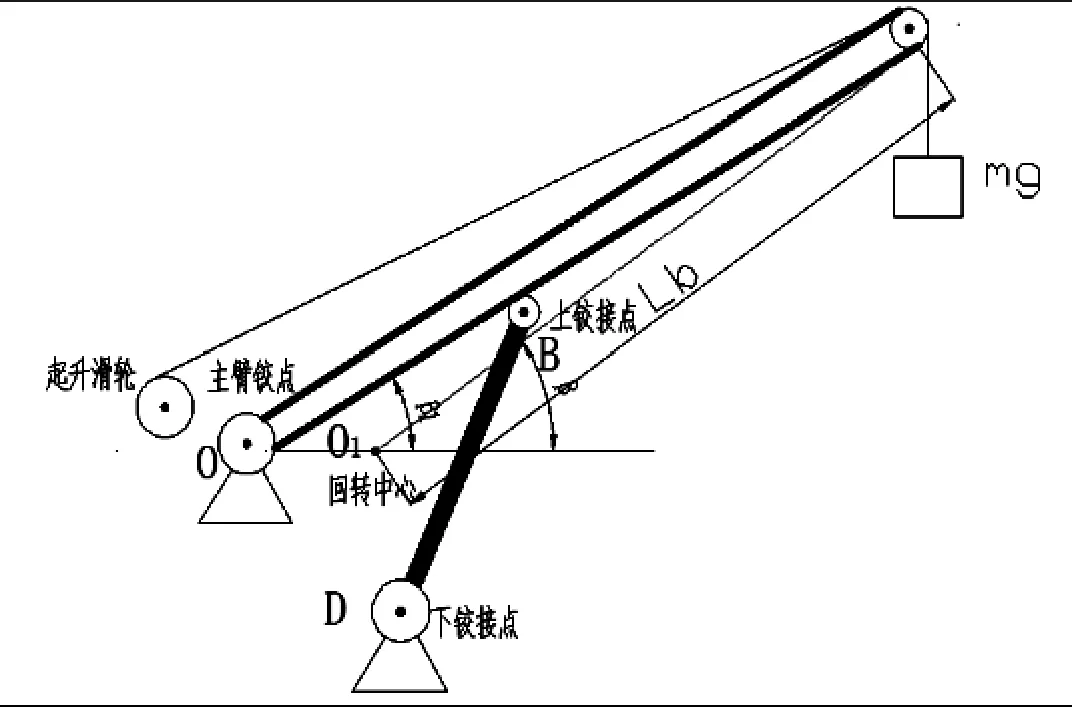
图1　汽车起重机工作模型示意图

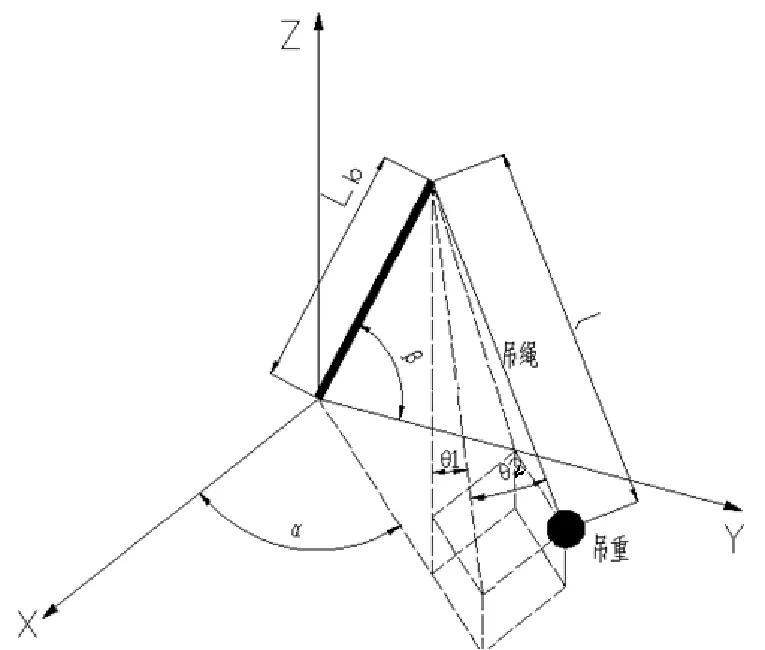
图2　汽车起重机简化图

为方便模型计算假设起重机主体及吊臂为刚体，支腿作用下回转台稳定，吊重视为质点，旋转过程中产生的摩擦力矩与吊钩质量忽略不计。

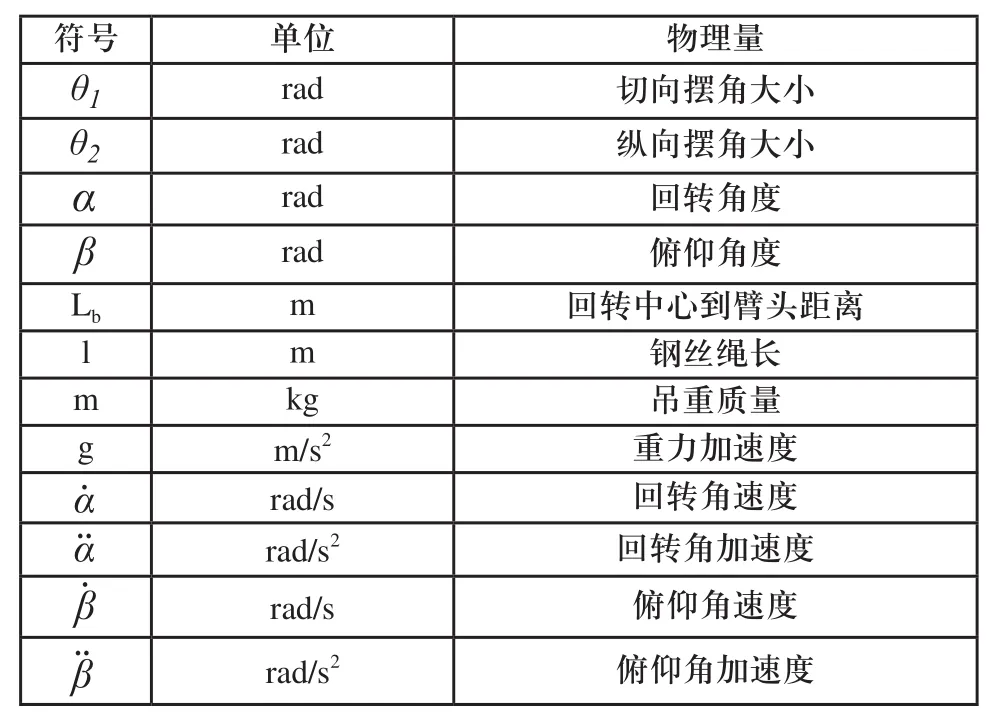
表1　各符号参数示意

利用拉格朗日分析力学，以切向摆角作广义坐标进行受力分析。建立如下Lagrange方程：

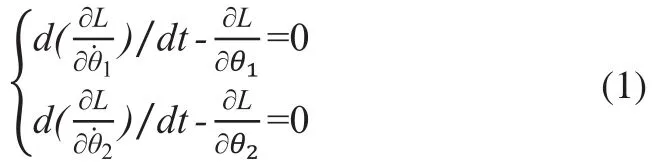
其中，L为拉格朗日算子，L=T-V，T为系统动能，V为系统的势能。

将各参数带入，系统两方程变为如下形式：

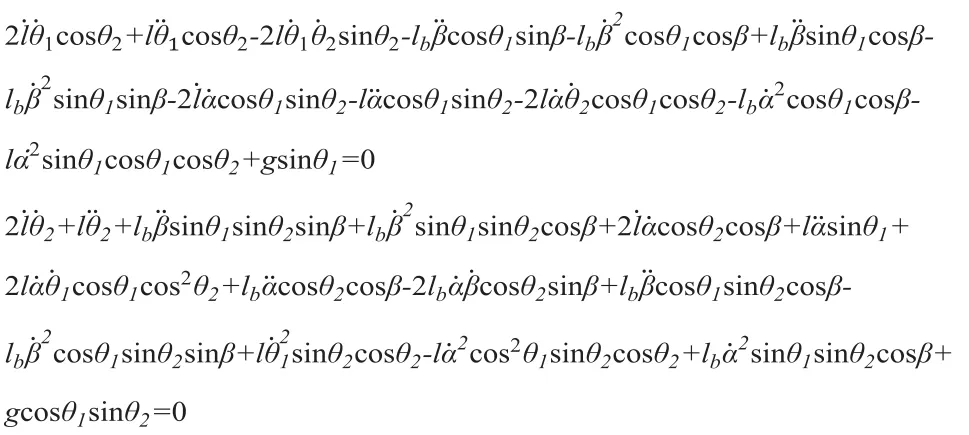
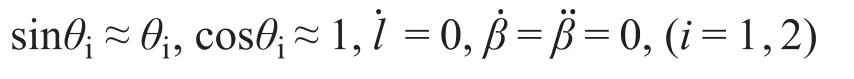
最终简化结果如下：

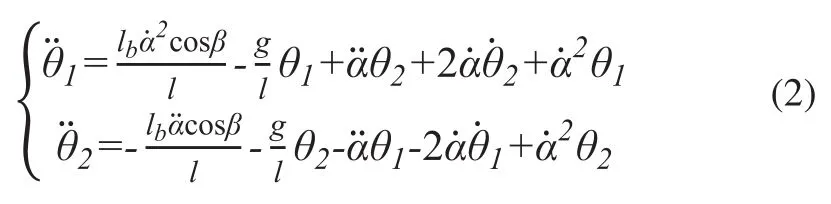
2　模型仿真实验

为了进行模型仿真需要对模型进行处理，需将动力学模型的数学形式转换为适用于计算机仿真的仿真模型。MATLAB是个十分优秀的软件平台，广泛的应用于控制系统的仿真设计等领域，使用其中的Simulink组件可以方便地建立系统模型，对系统进行仿真。

本文以某型汽车轮式起重机为研究对象，针对不同回转角速度，回转中心与臂头连线距离，绳长以及吊重m，利用MATLAB组件Simulink搭建系统仿真框图仿真两方向摆角变化趋势，作为理论分析结果。利用安装在吊绳上的陀螺仪（图3）测量Roll、Pitch两方向摆角以对应和的大小变化规律，对实测数据与理论结果进行对比以印证计算的动力学模型是否准确。系统Simulink仿真框图如图4所示。

图3　陀螺仪安装情况示意图

选取该汽车起重机最常用工况基本臂（13.1m）、变幅角度50°、绳长12m、吊重20t、阻尼因数取经验数据0.02进行回转Roll和Pitch摆角实际测量与仿真对比，结果如下。

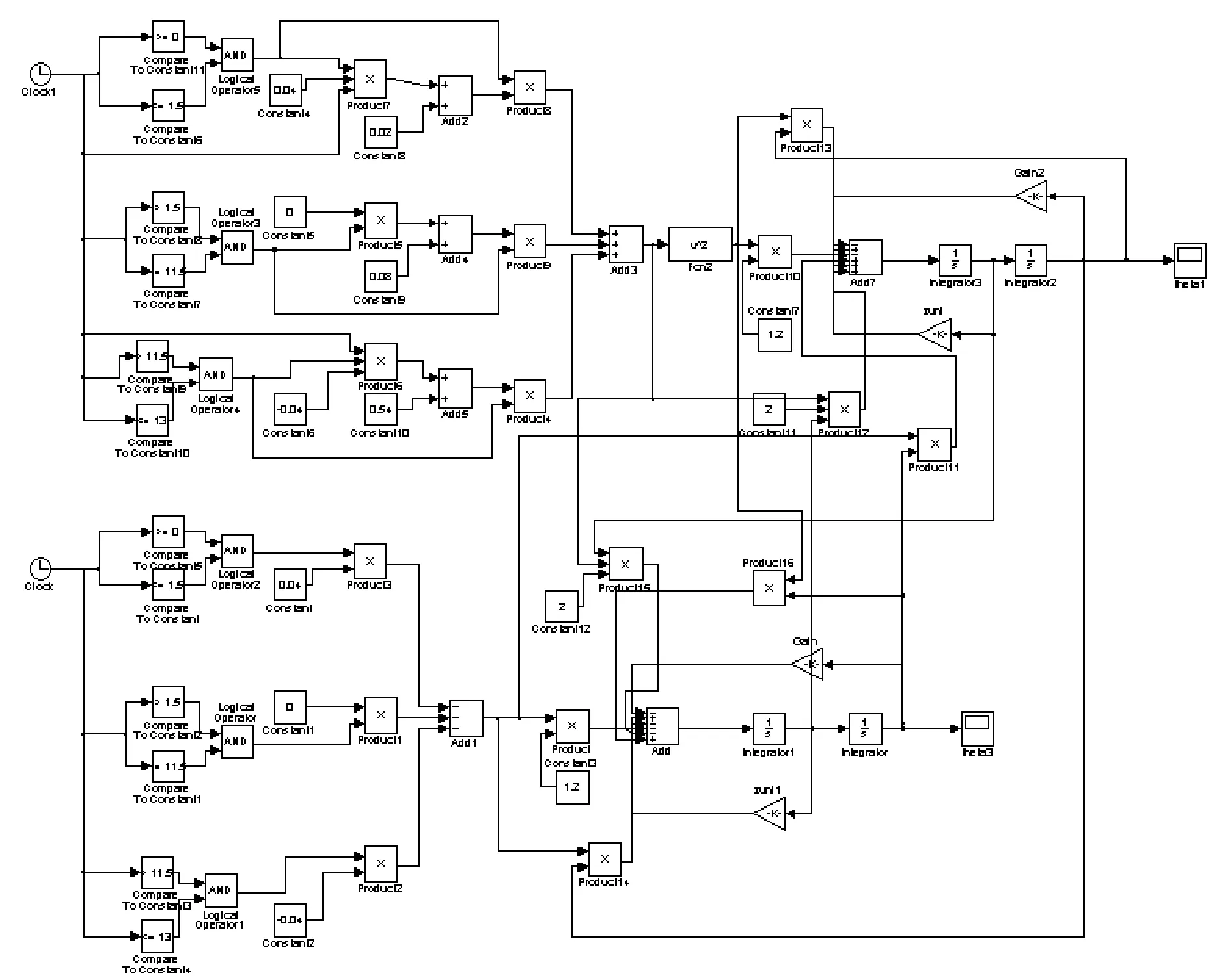
图4　基于MATLAB/Simulink搭建的系统仿真框图

图5　实测与仿真结果对比

由上仿真结果可以看出，陀螺仪实测与仿真结果最大摆角均发生在摆动个周期后，摆动波形十分相似且摆动衰减幅度基本保持致，该工况回转Roll方向角度最大值发生在15s左右大约在1.5rad以下，Pitch方向角度最大值也发生在15s左右均在0.1rad以下，基本可验证该动力学模型的准确性。

3　不同回转曲线摆角分析对比

3.1三角函数S曲线与等加速曲线

常用的控制算法等加速曲线包括3个阶段：恒加速阶段、匀速阶段、恒减速阶段，较易实现，但有载荷冲击。等加速曲线的速度和加速度曲线所示初始速度反应的是被控对象的动力性能，在实际应用中，可以根据被控对象的性能确定初速度大小，从而在定程度上可以变被控对象加减速时间。而汽车起重机无控制操作般只包括加速、匀速以及突然停止阶段，吊重摆角最大处是因骤停而造成的，因而两种曲线均会对防摆起到定作用。作者通过基于编码器回转实测角速度数据进行S曲线和等加速曲线拟合后利用已验证的动力学模型进行摆角大小对比，结果如图6所示。

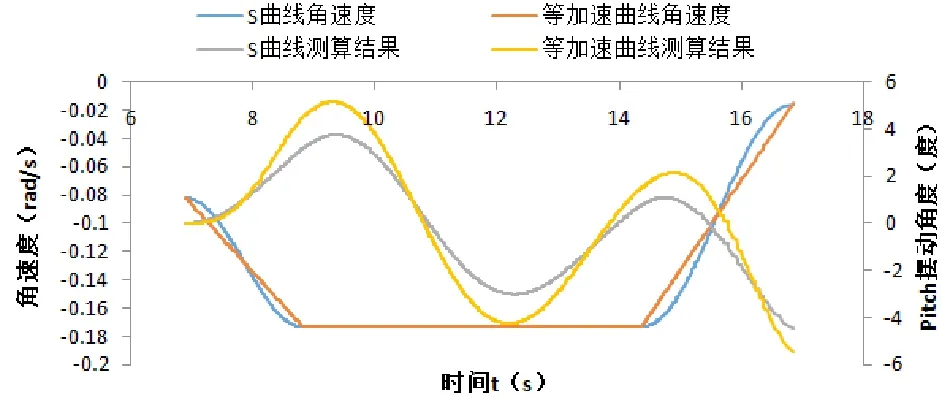
图6　三角函数S曲线与等加速曲线摆角大小对比

3.2五次多项式曲线与三角函数S曲线

本着不影响工作效率的想法，对回转测试数据进行多项式拟合，利用动力学模型解出摆角大小的离散解进行对比。然而多项式次数过高也不易实现，次数过低失真严重，最终优选五次多项式作为回转曲线算法与角函数S曲线抑制摆动效果作对比，其实现公式如下。

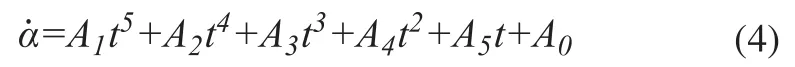
采用四阶-五阶Runge-Kutta法对建立的理论模型进行求离散解，从而推算出以此回转运动规律函数为输入变量下的吊钩双向摆动规律曲线，并将其结果与实测结果对比分析，找出摆动幅度较低的回转规律曲线类型，确定其影响参数，从而获得有效降低吊钩摆角幅度的策略。五次多项式与S曲线摆角抑制效果如图8所示（红线代表实测摆角，绿线代表五次多项式摆角，蓝线代表S曲线摆角）。

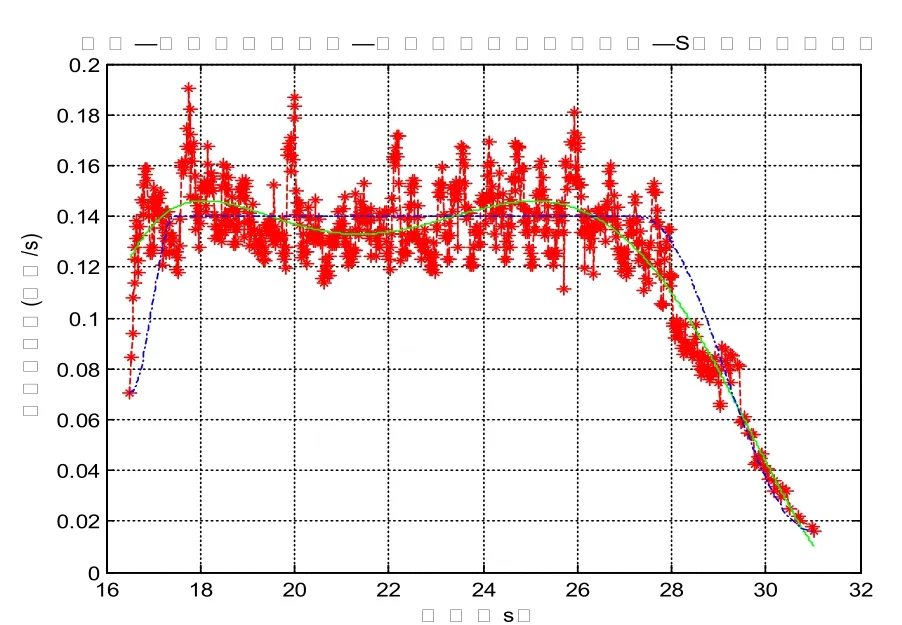
图7　基于实测数据的拟合曲线

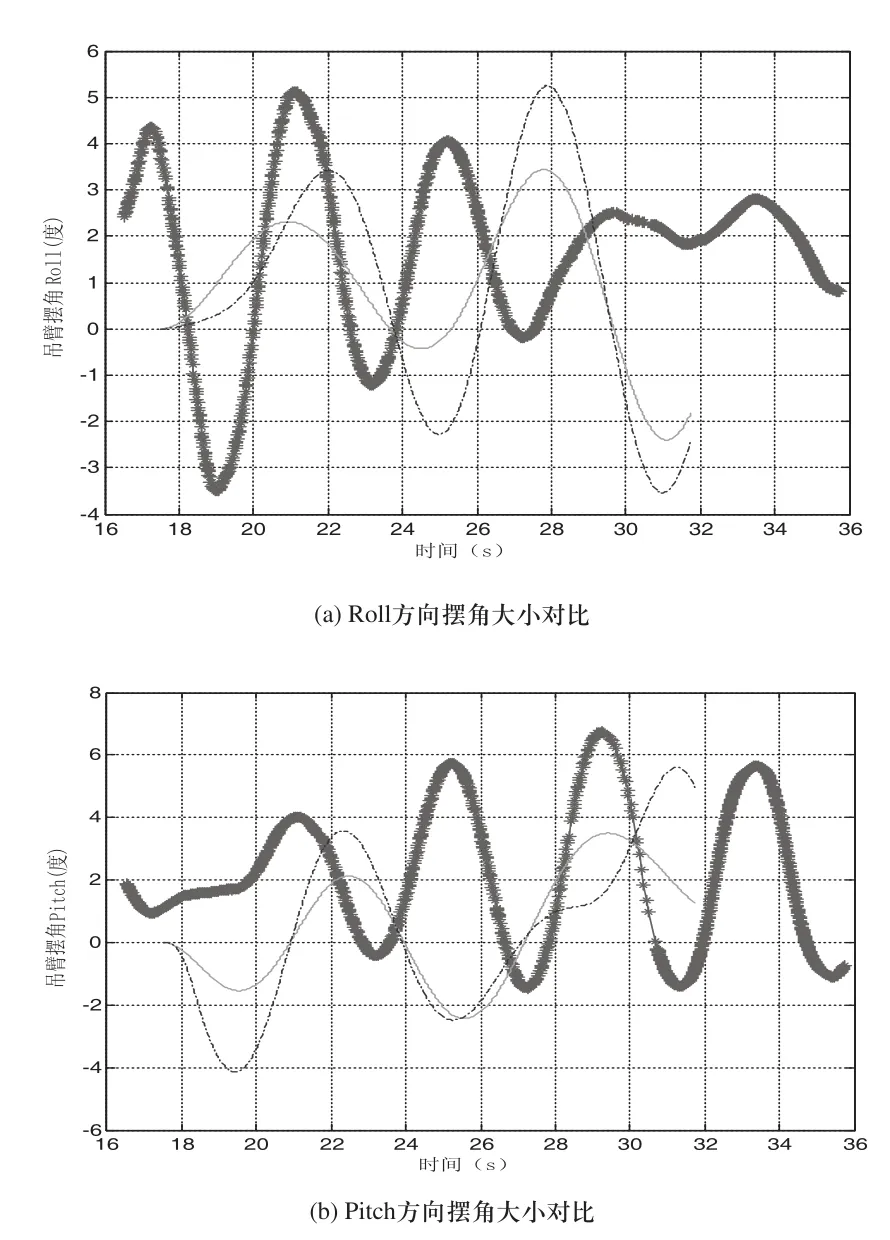
图8　两方向摆角大小对比

可见五次多项式在摆角抑制方面要优于S曲线，而且控制实现较S曲线要容易，因此可作为后续汽车起重机吊重防摆的种优选回转控制策略。

4　结论

本文对汽车起重机工作模型进行了简化，利用拉格朗日分析力学对简化模型进行计算得出动力学方程。利用MATLAB中Simulink组件动力学方程两方向摆角进行设定参数的仿真对比徐工集团XCT100型号汽车起重机最常用工况实测数据，得到Roll和Pitch摆角对比摆动规律、量级、衰减程度致，验证了动力学模型的正确性。基于此动力学模型提出利用等加速曲线、角函数S曲线以及五次多项式做修正后回转控制算法进行摆角大小计算对比，利用四阶-五阶Runge-Kutta法计算出离散解摆角趋势，得到五次多项式在吊重防摆方面为优于等加速曲线和角函数S曲线的算法，该算法植入控制器，可实现汽车起重机在回转吊运过程中吊重摆角的优化控制。

参考文献：

[1] 耿开辉.汽车起重机动力学仿真及运动可靠性研究[D].合肥工业大学,2015.

[2] 汽车起重机简介[J].机电设备船舶,2006,4:29-31.

[3] 王晓军,邵惠鹤.基于模糊的桥式起重机的定位和防摆控制研究[J].系统仿真学报,2005,17(4):936-939.

[4] 游谊,张自强,董燕,等.基于模糊控制的塔式起重机定位和防摆仿真实验[J].实验室研究与探索,2013,32(2):81-83.

[5] 陈志梅,孟文俊.龙门起重机的模糊滑模定位与防摆控制[J]. China Mechanical Engineering,2012(3).

[6] 任会礼,王学林,胡于进,等.起重船吊物系统动力响应仿真分析[J].系统仿真学报,2007,19(12):2665-2668.

[7] 王君凤.起重机吊摆系统的动力学分析与防摆控制研究[D].南京航空航天大学,2012.

[8] Uchiyama N, Ouyang H, Sano S. Simple rotary crane dynamics modeling and open-loop control for residual load sway suppression by only horizontal boom motion[J].Mechatronics, 2013,23(8):1223-1236.

作者简介：朱长建（1970 -），男，高级工程师，硕士，研究方向为工程机械制造。

收稿日期：2015-12-19

中图分类号：TH12

文献标识码：A

文章编号：1009-0134(2016)03-0112-05