基于正交实验的汽车-两轮车碰撞事故再现的参数影响研究*

胡 林,方胜勇,陈 强

(1.长沙理工大学,公路工程教育部重点实验室,长沙 410114； 2.长沙理工大学汽车与机械工程学院,长沙 410114；3.长沙理工大学,工程车辆安全性设计与可靠性技术湖南省重点实验室,长沙 410114； 4.中国汽车技术研究中心,天津 300162)

2016092

基于正交实验的汽车-两轮车碰撞事故再现的参数影响研究*

胡 林1,2,方胜勇2,3,陈 强4

(1.长沙理工大学,公路工程教育部重点实验室,长沙 410114； 2.长沙理工大学汽车与机械工程学院,长沙 410114；3.长沙理工大学,工程车辆安全性设计与可靠性技术湖南省重点实验室,长沙 410114； 4.中国汽车技术研究中心,天津 300162)

汽车-两轮车碰撞事故再现的关键是确定碰撞速度。本文在动力学分析的基础上建立了汽车与两轮车相互侧面碰撞的模型，得到了两车碰撞速度的表达式；筛选出影响汽车、两轮车碰撞速度推算和事故再现结果准确性的主要参数；通过具体的事故案例设定正交实验，分别获得了对汽车、两轮车的参数影响权重顺序；据此指导PC-Crash对一起真实的汽车-两轮车碰撞案例进行模拟重建。结果表明，按参数权重顺序辅助汽车-两轮车碰撞事故的再现仿真，可用较短时间再现与实际事故情况相吻合的结果。

汽车-两轮车碰撞；事故再现；碰撞模型；正交实验；参数影响

前言

据报道，世界各地每年有180 000名电动自行车驾驶者死于交通事故，且大多数发生在发展中国家[1]。我国汽车与两轮车(摩托车、电动自行车、自行车)发生的碰撞事故占有较大比例，是我国交通事故中的一种重要的事故形态。2012年我国共发生汽车-两轮车碰撞交通事故44 388起，导致10 922人死亡，直接财产损失10 252.1万元，分别占交通事故总起数、死亡人数量和财产损失的21.74%，18.2%和8.73%[2]。目前用于事故再现分析的软件主要有PC-CRASH[3]、SMAC[4]、CRASH[5]、清华大学的事故分析系统[6]、长安大学的TACAR[7]等。这些软件大多是以动量定理建立碰撞模型，同时引入碰撞中心的概念[8]。在实际运用时，由于事故过程中包含着很多的不确定参数，使对车辆碰撞速度的鉴定和碰撞事故过程的分析产生一定的不准确性，甚至某些参数的微小变化会引起碰撞模型计算结果产生较大的误差。文献[9]中对汽车-自行车碰撞事故车速的多值计算问题进行了研究，提出利用不同方法来进行多级综合评判。文献[10]中将不确定度分析方法引入汽车碰撞事故再现的模型算法中，以此推算车辆碰撞前速度的不确定度。文献[11]中对典型的碰撞模型中的碰撞前速度方向参数和碰撞中心位置参数进行了敏感度分析，给出了其数学表达式和适用范围。文献[12]中从碰撞前后阶段、碰撞阶段分别建立车对车碰撞事故参数敏感性模型，分析了事故再现系统的参数敏感性。这些研究主要是利用正向的数学解析计算模型来进行参数分析，在一定程度上明确了影响汽车碰撞事故车速计算的参数，而且可以较为准确地获得车辆的碰撞速度和碰撞点等物理量；但是这样的碰撞模型适用性不高，具体的碰撞模型只能对特定的事故类型进行分析，且往往要借助计算机。由于运用计算机软件进行模拟需要输入很多参数，且某些输入参数的准确度对输出的结果影响很大，因此，要得到一个很好的再现结果需要花费较长时间来进行输入参数的调整。如果可以确定影响再现结果准确性的各参数的权重，再有针对性地指导输入参数的调整，能够在较好获得仿真结果的同时大大缩短再现仿真的时间周期，而且对事故现场的勘查也具有现实的指导意义。

本文中以汽车-两轮车碰撞事故类型为例，利用正向的数学力学解析计算模型来分析影响碰撞速度计算的参数，再运用正交实验分析法对这些参数的权重进行排序，并将权重排序结果应用于国内一起真实的汽车-两轮车碰撞案例的PC-Crash重建，验证所提方法的有效性。

1 参数提取

1.1 汽车-两轮车碰撞事故再现过程

汽车-两轮车碰撞过程可分为3个阶段：(1)碰撞前阶段，驾驶员发现危险到两车刚开始接触；(2)碰撞阶段，两车刚开始接触到两车开始分离为止；(3)碰撞后阶段，两车开始分离到完全停止[13]。在实际事故再现中一般先根据路面的制动痕迹、停车位置和道路情况等使用轨迹模型来估算碰撞后的车辆速度，然后依据碰撞模型计算出碰撞时车辆的速度，最后利用计算出的结果和事故现场信息作为仿真软件的输入，模拟出碰撞过程并与事故现场结果进行比对，若不满意则按优化算法调整初始数据重新计算，也即用逆向计算来指导软件正向模拟。因此，建立合适的碰撞运动模型得到准确性较高的参数值对软件的模拟操作具有很大的实际指导意义。

1.2 汽车-两轮车侧面碰撞的运动模型

通常，汽车-两轮车碰撞事故类型可以分成3种情况：(1)两轮车迎面撞击汽车，即正面碰撞；(2)两轮车侧面遭到汽车撞击，即侧面碰撞；(3)两轮车被汽车追尾，即追尾碰撞。此外还有一种特殊情况，即同向刮擦，两轮车与汽车同方向并排行驶，当汽车右转弯时，两轮车因避让不及被汽车刮倒在地。通过对中国交通事故深入研究项目(China In-Depth Accident Study， CIDAS)2013年在广东佛山和吉林长春采集的142起汽车-两轮车碰撞事故进行统计分析，其中侧面碰撞占45%，正面碰撞占30%，是两轮车碰撞事故的两种主要事故形态，本文中主要对这两种事故类型进行研究。

1.2.1 汽车对两轮车的侧面碰撞运动模型

汽车与两轮车侧面碰撞事故如图1所示，碰撞发生后质量为m1的两轮车(编号01)沿与y轴夹角θ1的方向滑动L1距离后停止；骑车人则沿与y轴夹角θp方向飞出，抛出距离为LP；而汽车(编号02)则沿原来前进方向继续滑行L2后停止。

根据事故现场勘测得到的碰撞位置、制动痕迹、滑动痕迹和车体上的碰撞痕迹中心等信息，经正则化处理后可以推断出车辆的瞬间运动轨迹，从而得到车辆碰撞时刻的速度。

汽车-两轮车碰撞过程非常短暂，碰撞时撞击力很大。因此，可以运用动量守恒定律计算碰撞前汽车车速和两轮车速。在图1x方向上运用动量守恒定理可得

m2v20=m2v2+m1v1sinθ1+mpvpsinθp

(1)

式中：m1，m2和mp分别为两轮车、汽车和骑车人的质量；v20为汽车碰撞前速度；v1，v2和vp分别为两轮车、汽车碰撞后速度和骑车人抛出速度；θ1和θp分别为碰撞后两轮车滑动方向与y轴夹角和骑车人抛出角度。

由于两轮车系统质量(m1+mp)与汽车质量m2相差悬殊，碰撞过程中汽车在y方向的运动不显著，而且不易测出。故在y方向运用动量定理求解出的结果会造成较大误差。由于骑车人与两轮车在碰撞前是一起以v10的速度运动，与汽车碰撞后如果忽略摩擦力的作用，骑车人由于惯性作用在y方向将带着这个速度抛出。因此，可以把骑车人抛出速度vp的y方向分量作为两轮车碰撞前的速度，即

v10=vpcosθp

(2)

式(1)和式(2)中的汽车、两轮车碰撞后速度v1，v2和骑车人的抛出速度vp可以依据事故现场路面留下制动痕迹和滑动痕迹运用能量守恒和平抛运动公式来进行求解。

碰撞后骑车人被抛出，其在水平方向的运动距离为抛射运动距离和接触地面后的滑行距离之和，分别可由式(3)、式(4)和式(5)求解，即

Lp=x1+x2

(3)

(4)

(5)

得

(6)

式中：Lp，x1和x2分别为骑车人抛出总距离、抛射距离和滑行距离；g为重力加速度；h为骑车人的质心高度；μp为人体与路面间的摩擦因数，根据国外的实验数据取值为0.5～0.7(干燥混凝土或沥青路面)[14]。

两轮车碰撞后的速度v1可通过地面的滑动距离来求解：

(7)

可得

(8)

式中：L1为两轮车滑动距离；μ1为两轮车车身与地面的摩擦因数。

同理求出碰撞后汽车速度为

(9)

式中：L2为汽车制动印迹长度；μ2为汽车轮胎与地面的摩擦因数。

结合式(1)、式(2)、式(6)、式(8)和式(9)可求得碰撞前两轮车速和汽车车速为

(10)

(11)

由式(10)和式(11)可知，碰撞前两轮车和汽车的速度及其影响因素可表示为

v=f(fm1,fmp,μ2,μ2,μp,θp)

(12)

其中：fm1=m1/m2；fmp=mp/m2

1.2.2 两轮车对汽车侧面碰撞的运动模型

两轮车对汽车侧面的碰撞事故如图2所示，高速行驶的两轮车迎面撞击正在行驶中汽车的侧面。

同理，运用动量定理和能量守恒定理可得到碰撞前两轮车速和汽车车速为

(13)

(14)

式中：θ为碰撞前后汽车质心在x方向的偏转角。

由式(13)和式(14)可知，碰撞前两轮车和汽车的速度及其影响因素可表示为

v=f(fm1,fmp,μ,θ)

(15)

式中μ为汽车轮胎与地面摩擦因数。

根据逆向计算结果和事故现场信息，应用仿真软件模拟出碰撞过程是事故再现的第二步。运用PC-Crash软件进行事故重建，需要输入很多参数，这些参数的取值大多依赖于操作者的经验，这势必会对重建结果造成较大误差且需要较多的时间来进行参数调整，因此有必要对输入参数进行权重分析。通过上面对碰撞速度的分析，结合PC-Crash软件优化计算器中的参数和文献[15]中的研究结果，确定了11个对汽车-两轮车碰撞结果影响最大的参数：两轮车质量、两轮车车速、汽车车速、汽车质量、汽车与地面摩擦因数、两轮车与地面摩擦因数、汽车减速度、碰撞位置、两轮车质心高度、碰撞恢复系数和两车纵对称面的夹角。

2 参数权重分析

选用正交实验法来对这11个参数进行分析。基于某一真实案例建立了典型的汽车-两轮车侧面碰撞模型。在碰撞瞬间，汽车(编号01)车速为45km/h,两轮车(编号02)车速为20km/h，碰撞位置和碰撞后停止位置情况如图3所示。

2.1 确定实验指标做出因素水平表

取参数变化后仿真得到的两车最终位置(用两车质心坐标表示)与实际最终位置的偏移量y1和y2(以下简称偏移)作为实验指标，本实验共有11个重要参数，依据事故的实际情况设定3个水平，各因素水平为原模型参数的±5%，用A～K表示，不考虑因素间的相互作用，得到表1所示的因素水平表。

表1 因素水平表

2.2 选取正交表和依照实验方案获得实验结果

依据因素水平，不考虑因素间的相互作用，选择正交表L27(313)，由于要实验的因素是11个，所以有两列设置为空列。按实验序号在PC-Crash软件中对应设置参数进行仿真，结果如表2所示。

2.3 实验分析获得参数影响权重

方差分析可把实验指标数据总的波动分解为反映因素水平变化引起的波动和反映实验误差引起的波动两部分，然后将它们的平均波动进行比较，得出因素对指标作用效果是否显著的结论[16]。具体操作是把观测数据的总的偏差平方和SST分解为反映必然性的各个因素的偏差平方和SS(SSA，SSB，…，SSK)与反映偶然性的误差偏差平方和SSe，并计算它们的平均偏差平方和MS(MSA，MSB，…，MSK,MSe)；再获得各因素的均偏差平方和与误差均偏差平方和的比值F(FA,FB，…，FK)；最后对于给定的显著性水平α(本文α取0.1和0.05)查F分布表得到临界值Fα(f,fe)，将F值与临界值进行比较；以因素A为例，若F0.1(f,fe)F0.05(f,fe),因素A对实验指标影响非常显著。依此得到各个因素的显著性，越显著表示因素的影响权重越大。11个实验参数对两车位移指标的方差分析结果见表3和表4。

通过以上方差分析可知：所选的11个参数对两轮车影响权重的顺序依次为两车接触平面角、两轮车质心高度、汽车速度、两轮车速度、碰撞恢复系数、两轮车与地面摩擦因数、汽车与地面摩擦因数、汽车质量、两轮车质量、汽车减速度、碰撞位置；对汽车影响权重的顺序依次为汽车减速度、汽车速度、两轮车与地面摩擦因数、两轮车速度、汽车与地面摩擦因数、碰撞位置、两车接触平面角、汽车质量、碰撞恢复系数、两轮车质量、两轮车质心高度。另外通过比较表3和表4中F与Fα的值可知，汽车速度、两车接触平面角、两轮车质心高度、两轮车速度、碰撞恢复系数和汽车减速度这6个参数对汽车-两轮车碰撞结果影响最为显著。

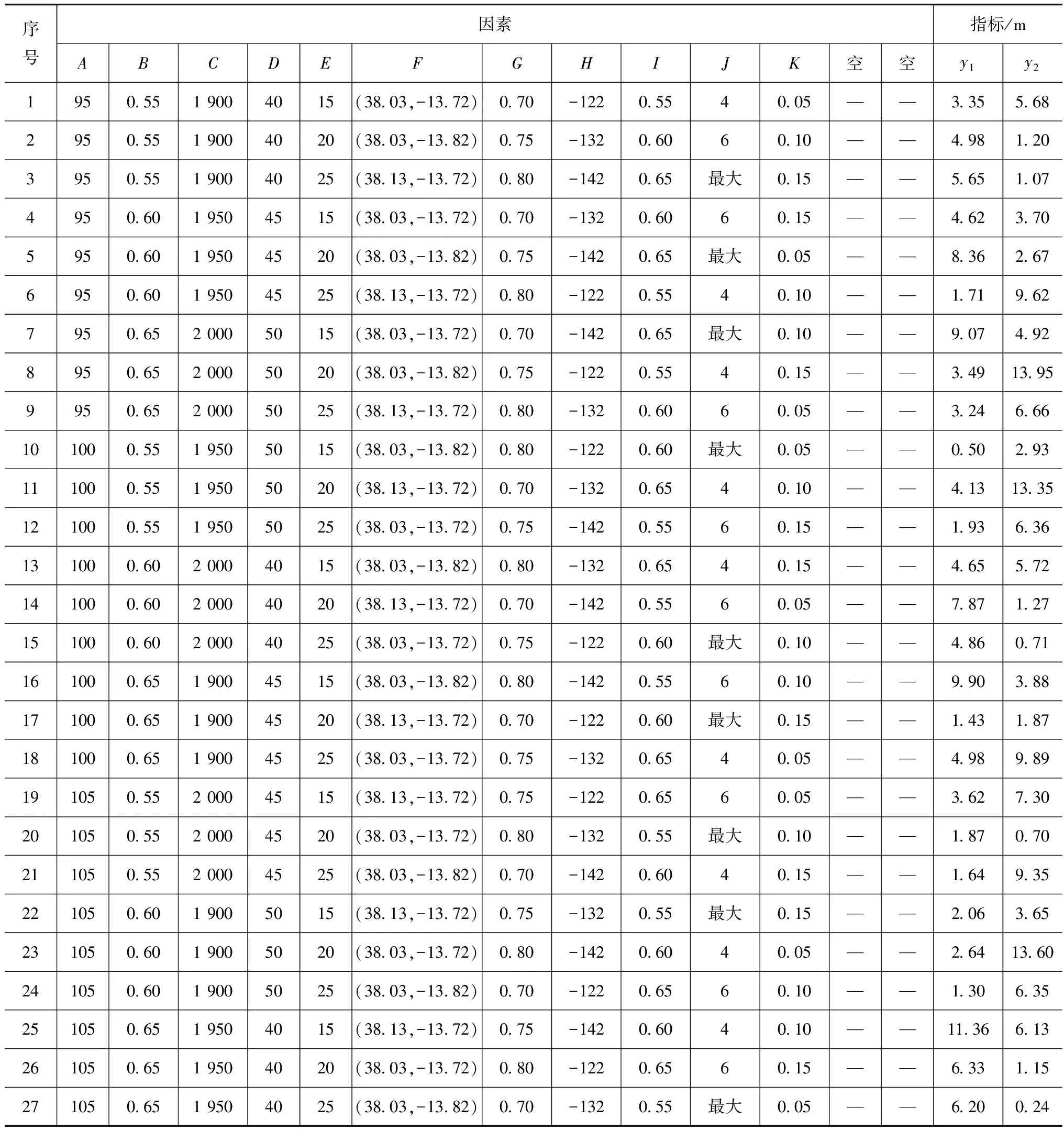
表2 L27(313)正交表

因此，在应用PC-Crash进行汽车-两轮车碰撞事故再现模拟时，若参与车辆的最终位移误差较大，可以针对性地调整汽车速度、两车接触平面角、两轮车质心高度、两轮车速度、碰撞恢复系数和汽车减速度等参数以达到加快得到满意仿真结果的目的。

3 案例验证

2013年某日下午，北京市丰台区南二环外环辅路，王某驾驶捷达出租车以40km/h速度由西向东行驶至菜户营桥东时，恰有孔某驾驶两轮车由北向南穿过马路。由于王某未按照规定让行，汽车前部与两轮车右侧相撞，造成两轮车骑车人孔某受伤，两车损坏的交通事故。图4为事故现场信息CAD图。依据事故现场得到的信息，在PC-Crash中输入汽车和两轮车的碰撞位置、速度、碰撞接触平面角等初始参数，在没有针对性地调整各个参数时难以得到较好的再现结果，而且也会增加两车碰撞后停止位置误差，如图5和图6所示。如果按照前面研究得到的参数权重来微调各个输入参数，能很快获得与实际情况尽可能吻合的碰撞后停止位置，如图7和图8所示。两车的位移误差在2%左右，汽车和两轮车的变形量与实际情况相符，故在误差值的允许范围内认为此次事故再现仿真获得的结果是合理的，验证了上述研究结论的准确性。

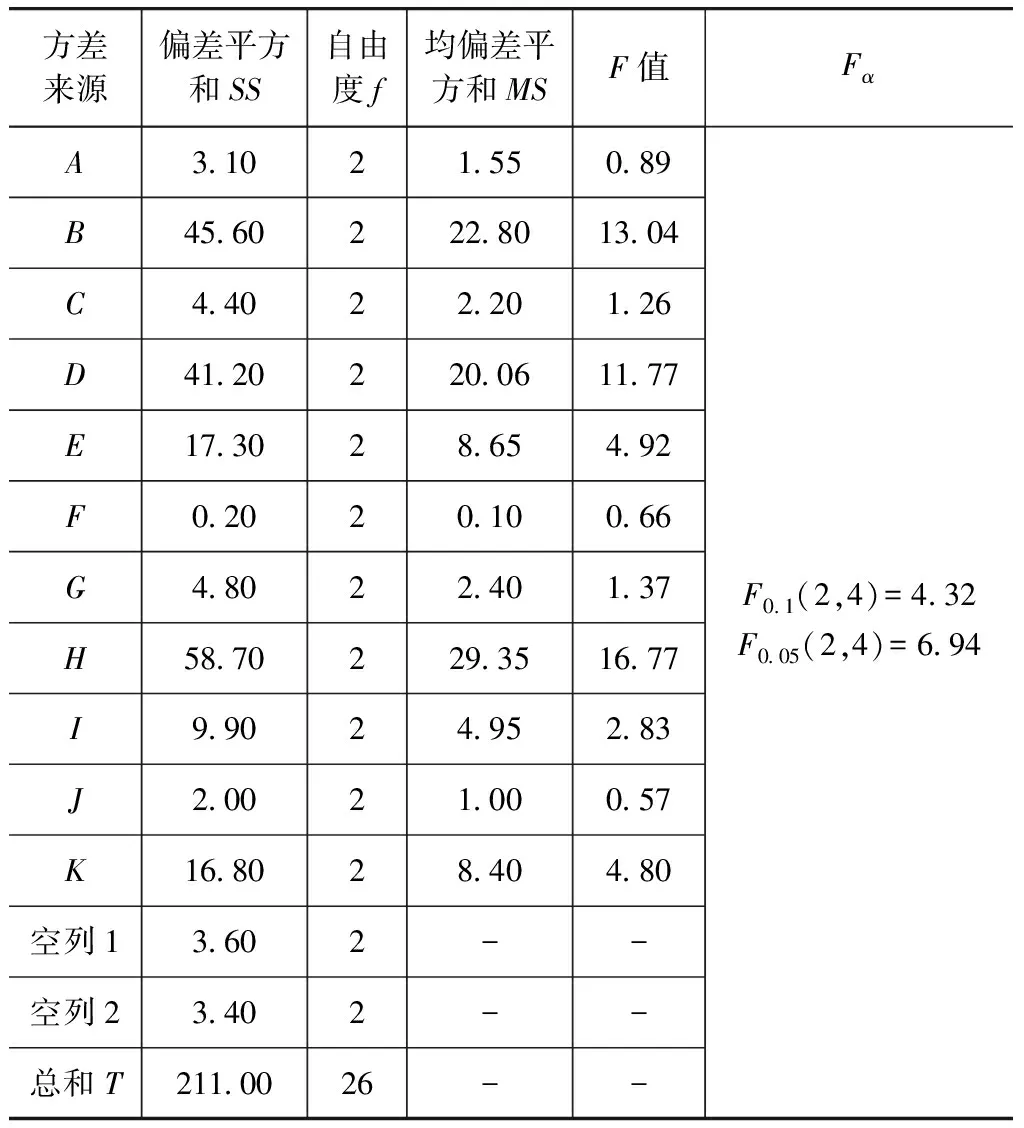
表3 两轮车位移方差分析表

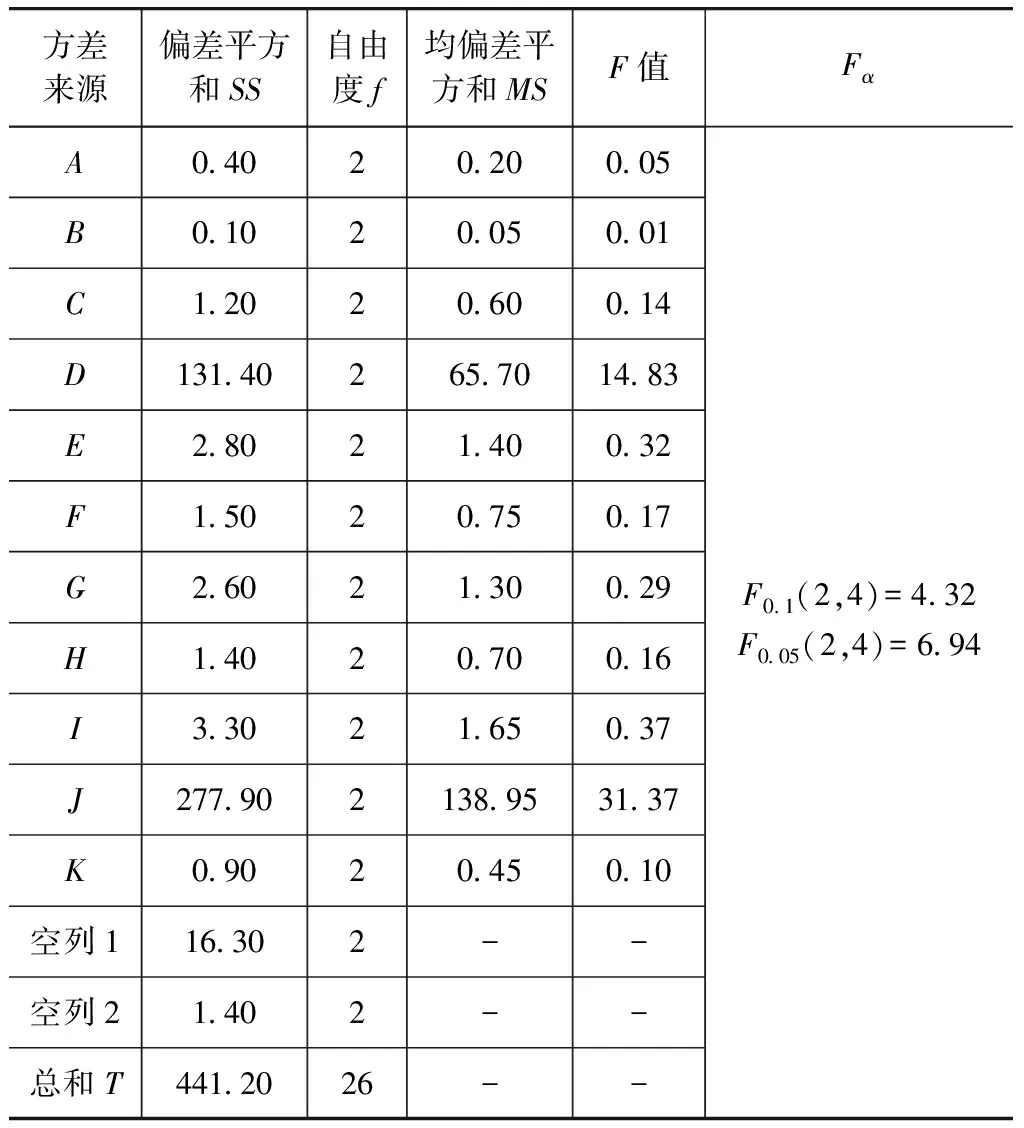
表4 汽车位移方差分析表

4 结束语

利用正交实验法对影响PC-Crash事故重建结果的11个参数的影响进行分析，得到其对汽车-两轮车碰撞再现结果影响的显著性顺序。结果表明，依据本文研究结论可指导事故现场勘查测量时有针对性地进行信息采集，在保证事故现场勘测的准确性和完整性的同时进一步提高事故现场处理效率；另外，依据参数权重指导参数推断和经验参数值的选取，以获得较高精度的再现结果。这为交通部门进行准确、客观地处理汽车-两轮车交通事故提供了良好的指导。但是，由于交通事故的类型多样，本文中只研究了汽车-两轮车相互侧面碰撞的事故类型，且在利用正交实验进行参数显著性分析时没有考虑各参数的交互影响，这将在今后做进一步的深入研究。

[1] QIANG Chen ,YONG Chen, OLA Bostrom ,et al. A Comparison

Study of Car-to-Pedestrian and Car-to-E-Bike Accidents: Data Source: The China In-Depth Accident Study (CIDAS)[C]. SAE Paper 2014-01-0519.

[2] 公安部交通管理局.中华人民共和国道路交通事故统计年报(2012年度)[R].北京:公安部交通管理科学研究所,2013.

[3] CLIFF W E,MONTGOMERY D T. Validation of PC-Crash-A Momentum-Based Accident Reconstruction Program[C]. SAE Paper 960885.

[4] PIOTR Swider, JAN Unarski, WOJCIECH Wach. SMASH Program for Car Accident Simulation[C]. SAE Paper 2000-01-0848.

[5] TERRY D Day, RANDALL L Hargens. Further Validation of Edcrash Using the Ricsac Staged Collisions[C]. SAE Paper 890740.

[6] 李一兵,陈云刚,吴卫东.CM 碰撞模型的建立及试验验证[J].清华大学学报(自然科学版),2001,41(11):98-101.

[7] 魏朗,陈涛,杨存义.车辆碰撞事故空间模拟再现系统开发研究[J].中国公路学报,2003,16(4):83-86.

[8] ISHIKAWA H. Impact Model for Accident Reconstruction-Normal and Tangential Restitution Coefficients[C]. SAE Paper 930654.

[9] 许洪国,高蔚,苏键,等.汽车交通事故碰撞速度多值问题的研究[J].中国公路学报,1996,9(1):87-93.

[10] 袁泉,李一兵.汽车碰撞事故再现估算速度的不确定度分析[J].汽车工程,2001,23(4):230-232.

[11] 裴剑平,李一兵,吴卫东.事故再现典型碰撞模型的参数敏感度分析[J].公路交通科技,2002(4):130-133.

[12] 陈涛,魏朗,龚彪,等.车对车碰撞事故再现系统的参数敏感性分析[J].汽车工程,2012,34(9):771-776.

[13] 陈涛,魏朗,高岩.车辆间碰撞交通事故计算机辅助鉴定技术综述[J].中国安全科学学报,2010,20(4):38-43.

[14] 林洋,上山胜,等.机动车事故鉴定方法[M].北京:群众出版社,1998:121.

[15] 王宏雁,邵文煜.基于PC-Crash的交通事故再现误差分析[J].同济大学学报(自然科学版),2009,37(4):531-536.

[16] 潘丽军,陈锦权.试验设计与数据处理[M].南京:东南大学出版社,2008:140-144.

A Research on the Parameter Influences of the Accident Reconstruction fora Car-motorcycle Collision Based on Orthogonal Experiments

Hu Lin1,2, Fang Shengyong2,3& Chen Qiang4

1.ChangshaUniversityofScienceandTechnology,KeyLaboratoryofHighwayEngineeringMinistryofEducation,Changsha410114; 2.SchoolofAutomotiveandMechanicalEngineering,ChangshaUniversityofScienceandTechnology,Changsha410114; 3.ChangshaUniversityofScienceandTechnology,HunanProvinceKeyLaboratoryofSafetyDesignandReliabilityTechnologyforEngineeringVehicle,Changsha410114; 4.ChinaAutomotiveTechnologyandResearchCenter,Tianjin300162

The key to the accident reconstruction of car-motorcycle collision is the determination of collision speeds. In this paper, the models for two mutual side collisions between car and motorcycle are set up based on kinetic analysis, with the collision speed expression of two vehicles obtained. The main parameters influencing the accuracies of collision speed reckoning and accident reconstruction are selected. For a specific accident case, orthogonal experiments are performed to obtain the significance order of parameter effects of two vehicles, and based on which as a guide, a reconstruction of a real car-motorcycle crash case is conducted with PC-Crash. The results show that the accident reconstruction of car-motorcycle collision assisted by parameter weight order can reproduce a result well agreeing with real case in shorter time.

car-motorcycle collision; accident reconstruction; collision model; orthogonal experiments; parameter influences

*国家自然科学基金(51475048)、湖南省自然科学基金(2015JJ2001)、湖南省教育厅科研项目(13C1015)和公路工程教育部重点实验室开放基金资助。

原稿收到日期为2015年1月29日。