深度混合动力系统发动机起动控制研究*

王 晨,王 博

(1.同济大学汽车学院，上海 201804； 2.吉利电子传动有限公司,上海 201501)

2016089

深度混合动力系统发动机起动控制研究*

王 晨1，2,王 博2

(1.同济大学汽车学院，上海 201804； 2.吉利电子传动有限公司,上海 201501)

本文旨在对深度混合动力系统的发动机起动控制进行研究。首先，推导了新型拉维娜功率分流机构的动力学方程，应用杠杆法分析不同挡位下起动控制的方法。接着在设定了工程目标、考虑了诸影响因素的基础上设计了功能模块框架和接口，使用Matlab/Simulink软件搭建了发动机起动控制模型，并进行了联合仿真。最后，将起动控制模型集成到混合动力系统模型中，生成代码后下载到控制器中，在搭载了新型拉维娜功率分流机构的深度混合动力车上进行了NEDC循环的验证。

深度混合动力系统；拉维娜行星机构；起动控制

前言

随着全球能源和环境问题日益突出，在当前电池的续航能力和使用寿命受限条件下，研究和发展混合动力车有重要的意义。

发动机作为混合动力系统的主要动力来源，对它的控制是否合理，直接关系到整车的动力性、经济性、排放和驾驶性能。

近年来，一些学者在搭载了4速AT变速器的混合动力车辆上进行了发动机stop-start结构和性能的研究，并与传统轿车进行了对比[1]；文献[2]中在插电式混合动力车辆上进行了发动机起停控制策略的优化研究，认为动力电池荷电状态(SOC)可以作为PHEV发动机起停的判断条件；文献[3]～文献[6]中对BSG结构的混合动力车柴油发动机起停控制进行了全面的阐述和研究，包括前期调研、模型仿真和控制策略的开发。这些研究的结果表明，在混合动力车辆的发动机上，采用起停控制技术可以降低排放和油耗，通过推迟点火角和平滑撤去起动电机转矩可以减小起动冲击。但在拉维娜或相近类型行星变速机构基础上完整研究发动机起动控制策略的论文尚少。

目前，丰田PruisⅢ[7]采用了阿特金森循环发动机和用来进行整车功率的分流的单行星排三轴传动变速机构，整车百公里油耗较低(4L)，与这次研究采用的功率分流机构相比，其结构相对简单。

本文中在新型拉维娜混合动力变速器基础上，推导了动力学方程，使用杠杆法对发动机起动模式进行了分析，设计了完整的起动功能模块，配合车辆物理模型和混合动力系统控制模型进行了离线仿真，生成代码并下载到控制器中进行实车验证。本研究可为混合动力系统及其控制系统功能模块的开发、仿真和试验研究提供参考。

1 混合动力系统方案

1.1 功率分流装置

功率分流采用双行星排结构，如图1所示。图中：S1为小太阳轮，P1为前排轮系短(粗)行星轮；S2为大太阳轮，P2为后排轮系长(细)行星轮；C为前后排轮系共用的行星架；R为轮系共用齿圈。

从图1中可见：P1分别与S1，P2和齿圈啮合；P2与S2和P1啮合。

1.2 动力学方程

根据行星齿轮运动学方程[8]得前、后排轮系各运动部件的转速关系式为

ωS1+ρ1·ωR=(1+ρ1)·ωC

(1)

ωS2-ρ2·ωR=(1-ρ2)·ωC

(2)

式中：ωS1为前排轮系小太阳轮角速度；ωS2为后排轮系大太阳轮角速度；ωR为共用齿圈角速度；ωC为行星架角速度；ρ1，ρ2分别为前、后排轮系传动比，ρ1=ZR/Z1，ρ2=ZR/Z2，Z1，Z2和ZR分别为太阳轮S1，S2和齿圈R的齿数。

根据行星齿轮动力学方程[9]得前、后排轮系各运动部件转矩与齿轮啮合力之间的关系式为

TS1=-F1·rs1

(3)

TC1=F1·(rs1+r0)

(4)

TC2=F2·(rs2-r0)

(5)

TC=TC1+TC2

(6)

TS2=-F2·rs2

(7)

TR1=-F1·r0

(8)

TR2=F2·r0

(9)

TR=TR1+TR2

(10)

式中：TS1为前排轮系小太阳轮转矩；TS2为后排轮系大太阳轮转矩；TC1，TC2分别为前、后排轮系作用在行星架上的转矩；TC为前后排轮系作用在行星架上的转矩之和；TR1，TR2分别为前、后排轮系作用在齿圈上转矩；TR为前后排轮系作用在齿圈上的转矩之和；rs1为前排轮系小太阳轮半径；rs2为后排轮系大太阳轮半径；r0为共用齿圈半径；F1，F2分别为前、后排轮系齿轮啮合力。

由以上各式可得

TR+TC+TS1+TS2=0

(11)

TR-TS1·ρ1+TS2·ρ2=0

(12)

1.3 杠杆等效图

采用杠杆法[10]对上述新型拉维娜装置的前、后排轮系进行结构等效,如图2所示。

图中虚线杠杆与各轴系相交，交点到水平线的垂直距离分别表示为ωS1，ωC，ωR和ωS2，以行星架为支点时，ωC=0，S1轴与C轴的水平距离为ρ1，R轴与C轴的水平距离为1，S2与C轴的水平距离为ρ2。

1.4 混合动力变速器方案

在新型功率分流装置的基础上，配置电机和发动机作为动力输入，通过外齿圈输出动力，构成了混合动力变速器，如图3所示。图中：S1为小太阳轮；S2为大太阳轮。

发动机经扭转减振器与行星架相连，电机E2与后排大太阳轮相连，电机E1与前排小太阳轮相连，3者动力经共用齿圈复合后传递至输出端。忽略扭转减振器的影响，搭载该混合动力变速器的整车动力学拓扑如图4所示。

图中：PG1和PG2分别为前后排行星轮系；Out为变速器动力输出端；K为减速器传动比；Vehicle为整车端；TE1和TE2分别为电机E1和E2的驱动转矩；TEng为发动机驱动转矩；Tf为输出齿圈转矩。

忽略行星轮转动惯量，变速器各轴系动力学关系为

(13)

(14)

(15)

(16)

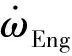
2 发动机起动模式分析

2.1 驻车起动模式

驻车工况时，齿圈R由驻车(P)挡机构锁止，小电机E1、大电机E2和发动机ICE均处于待机模式。当动力电池电量低于某值，或者水温较低，整车管理系统向小电机E1发出进入拖转发动机模式指令，小电机施加驱动转矩TE1，克服阻力做功，将发动机拖转至预设目标转速，此时发动机开始喷油并迅速完成起动过程，输出驱动转矩TEng，小电机E1输出制动转矩为动力电池充电，大电机E2始终保持随动，输出齿圈转矩Tf由P挡机构提供。驻车起动模式等效杠杆图如图5所示。

2.2 前进行车起动模式

2.3 倒车起动模式

3 工程设计目标与分析

3.1 平顺性

良好的起动平顺性是混合动力发动机起动控制算法设计的目标。发动机摩擦力矩[11]、施加在发动机轴上的拖转转矩与梯度和扭转减振器的参数是影响起动平顺性的主要因素。

3.2 动力性

驾驶员有较大的加速需求或者按下运动模式开关时，需要发动机起动并快速提供转矩。喷油点火时刻、发动机转矩加载梯度和电机电池的能力是影响动力性的主要因素。

3.3 油耗和排放特性

混合动力发动机起动控制算法还必须综合考虑整车的油耗和排放要求，发动机进入闭环控制的时间、目标喷油转速、点火角、起动时刻的空燃比配置和冷机状态下的发动机负载是主要影响因素。

4 起动算法的设计与仿真

4.1 起动算法接口

起动算法的输入和输出如图8所示，输入包括：发动机的转速、摩擦力矩、喷油和点火正时信息(以发动机表示)；挡位位置信息(以整车表示)；电池能力(以电池表示)；驾驶员需求(以变速器表示)；制动能量回收转矩基础需求(以制动能量回收表示)和电机能力(以电机表示)等。输出包括发动机、电机、车辆、制动能量回收转矩需求和各状态切换的标志位。

4.2 起动算法

起动算法由起动方式判断、状态切换和转矩结构组成，如图9所示。

起动方式根据驾驶员需求和发动机水温分为低速起动和高速起动。低速和高速起动都由电机E1执行转矩将发动机拖转到目标喷油转速完成，与低速起动相比，高速起动具有目标喷油转速高、起动时间长、平顺性好的特点。起动方式判断模块还包括喷油点火时刻的设置、节气门开度设置和进气压力的判断，如图10所示。

状态切换是指系统满足起动发动机的条件后，根据发动机转速来进行起动状态的识别，在起动的不同时刻为电机E1转矩加载和发动机角加速度调节提供输入条件，状态切换如图11所示。

4.3 离线仿真结果与分析

在Matlab/Simulink环境下建模并进行仿真，结果如图12～图15所示。

由图12～图14可见，车辆在驻车(P)挡起动发动机时，发动机转速与行星架转速吻合较好，车速一直保持为0，电机E1施加的拖转转矩平滑；倒车(R)挡时，车辆由纯电动工况切换到发动机起动工况，电机E1转矩由负向变化为正向，将发动机拖转到目标转速，发动机转速与行星架转速基本一致。从车速变化趋势可以看出，在发动机起动过程中，整车驱动转矩受到限制，这是电池功率保护所致；前进(D)挡仿真时，节气门开度60%，纯电动工况运行0.5s后起动发动机，从结果中可以看出，电机E1转矩在发动机起动瞬间有一个突变，这是系统为了保证起动成功限制整车驱动转矩所致，根据行星系统的动力学原理，电机E2的转矩也会出现波动；电机转矩突变，导致折算到行星架输入轴上的拖动转矩突变，这通过扭转减振器缓冲后传递到发动机曲轴上，导致了由曲轴位置信号计算得出的发动机转速出现了波动。R和P挡下起动发动机时，电机E1转矩曲线平滑，未出现D挡的转速波动现象。

在发动机起动结束末期需要进行起动是否成功的检查，以确定是否可以开始转矩加载；当系统进入起动的第3阶段，即起动末期，此时用于拖转的电机E1转矩趋于稳定，如果发动机转速没有下降的趋势，且发动机反馈的实际输出转矩与需求转矩接近，维持一段时间，则认为起动结束。

由图15可见，与高速起动方式相比，低速起动完成的时间缩短了一半；高速起动和低速起动在拖转转矩与梯度、拖转功率、点火角设置、空燃比、节气门开度和目标转速的设置上均有所区别。与高速起动相比，低速起动拖转转矩加载的梯度较大，拖转功率被限制以保护电池，点火角提前较小，其它各项在此不具体说明。从平顺性角度看，低速起动方式的转速波动比较明显，平顺性较差。

5 实车验证

在离线仿真的基础上，将起动模型集成到混合动力控制系统模型中并生成代码，在某深度混合动力车上进行NEDC循环验证。电机、电池和发动机参数见表1，发动机转速、车速、油耗(以CO2排放表示)和SOC变化曲线见图16，空燃比、点火角和发动机水温变化曲线见图17，排放特性曲线见图18。按照国五排放标准规定，整个NEDC循环工况的百公里综合油耗为5.9L，HC排放为0.031g/km，CO排放为0.112g/km，NOx排放为0.011g/km，NMHC排放为0.028g/km。

在零下不同温度点进行了低温起动验证，发动机转速曲线如图19所示。由图可见，在-9，-24和-30℃低温环境下，系统执行低速起动，电机能将发动机拖转到预定目标转速，起动过程可以成功完成；随着温度的降低，起动过程转速的波动增大，经过分析认为，低温环境下起动过程的平顺性与发动机阻力矩的波动、电机拖转转矩加载方式和发动机燃烧特性有关。

表1 关键零部件参数

倒车起动模式验证试验结果如图20所示。由图可见，起动过程中，行星架转速和发动机转速均有不同程度的抖动。与发动机转速波动相比，行星架转速波动的频率较高，这是电机进行消除抖动转矩干涉所致。

与传统汽油车相比，本研究的混合动力车发动机飞轮与行星架输入轴之间没有离合器，在起动过程中，发动机的振动通过动力总成传导到车身上，给驾驶员带来冲击。后续的工作将从结构入手，深入研究起动过程的抖动问题，优化控制策略，以达到良好的起动平顺性。

6 结论

(1) 在产品级混合动力变速器的基础上，推导了新型功率分流机构的动力学公式，并进行了杠杆简化。

(2) 利用杠杆法分析了混合动力车不同挡位下的发动机起动过程，包括工作原理和控制方法。

(3) 预设了发动机起动控制的工程目标，并提前考虑了影响目标的各种因素，设计了功能模块的通信接口和控制策略，并对算法进行了分析。

(4) 利用Matlab/Simulink软件搭建了混合动力变速器、整车物理模型和起动控制模型，分别在3种挡位下对发动机起动控制进行了功能仿真验证，其中P挡、R挡下发动机转速比较平滑，D挡下发动机转速出现振荡；高速和低速起动方式对比仿真结果显示，与高速方式相比，低速方式发动机起动完成的时间缩短一半，但平顺性较差。

(5) 针对设计的起动策略，在实车上进行了国五排放试验，并进行了低温起动和倒车起动试验验证。结果显示：经济性方面，与搭载相同型号发动机的传统汽油车(百公里油耗为7.5L)相比，混合动力车的百公里综合油耗为5.9L，节油20%以上(考虑了电池电量下降折算的油耗)；动力性方面，设计了两种起动方式，在驾驶员有动力性优先的需求时，系统采用低速起动，与高速起动相比，低速起动可以缩短发动机完成起动过程的时间，提前供给转矩；排放方面，采用了精确优化的空燃比、点火角控制，合适的转矩加载，全面达到国五排放标准(采用国四催化转换器)；平顺性方面，在发动机起动瞬间，车辆存在轻微抖动的现象。

[1] TAMAI G, HOANG T, TAYLOR J, et al. Saturn Engine Stop-Start System with an Automatic Transmission[C]. SAE Paper 2001-01-0326.

[2] LI Xianjing, LI Liguang, SUN Yongzheng, et al. Optimization of Control Strategy for Engine Start-stop in a Plug-in Series Hybrid Electric Vehicle[C]. SAE Paper 2010-01-2214.

[3] CANOVA M, GUEZENNEC Y, YURKOVICH S. On the Control of Engine Start-Stop Dynamics in a Hybrid Electric Vehicle[J]. Transactions of the ASME,2009,11(131):061005-1.

[4] CANOVA M, GUEZENNEC Y, YURKOVICH S, et al. Control of the Start/Stop of a Diesel Engine in a Parallel HEV: Modeling and Experiments[C]. Proceedings of the ASME International Mechanical Engineering Congress and Exposition,2006.

[5] CANOVA M, GUEZENNEC Y, YURKOVICH S, et al. Control of the Start/Stop of a Diesel Engine in a Parallel HEV with a Belted Starter/Alternator[C]. Eighth International Conference on Engines for Automobile,2007.

[6] CANOVA M, GUEZENNEC Y, YURKOVICH S, et al. Model-Based Control for Diesel Engine Start/Stop Operations with a Belted Starter/Alternator[C]. Proceedings of the ASME International Mechanical Engineering Congress and Exposition,2007.

[7] ZHANG Xiaowu, LI Chiao-Ting, DONGSUK Kum, et al. Prius+ and Volt-: Configuration Analysis of Power-Split Hybrid Vehicles with a Single Planetary Gear[J]. IEEE Transactions on Vehicular Technology,2008,16(6):3544-3552.

[8] 葛安林.车辆自动变速器理论与设计[M].北京:机械工业出版社,1991.

[9] 冯力平,袁建民,李书江.用行星轮系运动特性方程计算自动变速器传动比的方法探讨[J].石家庄理工职业学院学术研究,2009,4(2):14-17.

[10] BENDORD H, LEISING M. The Lever Analogy: a New Tool in Transmission Analysis[C]. SAE Paper 810102.

[11] 李红朋,秦大同,杨阳,等.汽车发动机起动过程的动力学仿真[J].重庆大学学报,2005,28(6):4-6.

A Study on Engine Start Control in a Full Hybrid Electric Vehicle

Wang Chen1,2& Wang Bo2

1.SchoolofAutomotiveStudies,TongjiUniversity,Shanghai201804; 2.GeelyElectricTransmissionTechnologyCo.,Ltd.,Shanghai201501

The engine start control of a full hybrid power system is studied in this paper. Firstly the dynamics equations for a new Ravigneaux planetary power split mechanism are derived, and the start control method under different gear positions are analyzed with lever analogy technique. Then based on engineering objective defined with consideration of various influencing factors, the functional module framework and interfaces are designed, an engine start control model is built with Matlab/Simulink software and a co-simulation is conducted. Finally the engine start control model is integrated into hybrid power system model with corresponding code generated and downloaded to controller, and a NEDC cycle verification is performed on a full hybrid electric vehicle equipped with Ravigneaux planetary power split mechanism.

full hybrid power system; Ravigneaux planetary mechanism; start control

*国家高技术研究发展计划(2011AA11A20)和国家自然科学基金(51275355)资助。

原稿收到日期为2015年1月14日，修改稿收到日期为2015年4月9日。