预瞄跟随驾驶员模型校正环节参数求解方法

管 欣,陈永尚,贾 鑫，张立增，詹 军

(吉林大学，汽车仿真与控制国家重点实验室，长春 130022)

2016148

预瞄跟随驾驶员模型校正环节参数求解方法

管 欣,陈永尚,贾 鑫，张立增，詹 军

(吉林大学，汽车仿真与控制国家重点实验室，长春 130022)

预瞄跟随驾驶员模型中校正环节参数准确与否直接影响位置控制的精度。由于该参数与速度的关系具有强非线性难以直接求出，且对于多自由度复杂车辆模型，简单的等效2自由度法难免带来位置跟随的误差。本文提出一种任意车速下校正环节参数的求解方法。首先求解两个特定车速下的相关参数，进一步推导出校正环节参数关于速度的关系表达式。在MATLAB/Simulink中对CarSim C级车进行双移线和蛇行仿真试验。结果表明，采用以所提出的求解方法求出的参数的驾驶员模型跟随性较好，用于人-车闭环仿真有较高的精度。

车辆；驾驶员模型；校正环节；参数求解

前言

驾驶员转向控制模型的研究根据有无预瞄环节，分为补偿校正模型和预瞄跟随模型[1-2]。预瞄跟随模型考虑了驾驶员的前视作用，在人-车闭环系统评价和智能车辆控制领域应用广泛[3-5]。该模型包含7个物理参数：神经反应延迟时间td、动作惯性滞后时间Th、校正环节增益系数C0、微分校正系数TC、跟随器3阶参与系数a、预瞄时间Tp和方位预瞄作用系数λ。其中td和Th属生理学范畴，不做讨论。Tp，a和λ3个参数与驾驶员特性有关，作者在文献[6]中用误差分析法对其求解。模型中校正环节是对最优侧向加速度进行校正确定一个最优预瞄转向盘转角，其参数准确与否直接影响车辆侧向位置控制的精度。因此，本文中主要研究校正环节相关参数C0和TC的确定方法。

研究表明，C0和TC与汽车侧向稳态增益Gay和1阶时间常数Ty1、T1有关[7]。对于复杂多自由度车辆模型或真实车辆，Gay、Ty1和T1很难直接计算。文献[8]中给出通过转向盘角阶跃试验求出某一速度下汽车稳态增益与1阶时间常数的方法，但此方法只能针对某一特定速度。文献[9]中从线性2自由度车辆模型中将车速分离，可以将某一车速下的传递函数外推到任意车速下，且在线性区内有较高精度。但该方法要求在试验车速下辨识传递函数的全部系数，工作量大且精度较低。文献[10]中通过最小二乘法辨识Gay和TC，并且用三次样条曲线拟合出其关于速度的表达式，但此方法工作量巨大，过程中出现误差和错误易导致控制效果变差。

为此，提出一种试验法求解任意车速预瞄跟随驾驶员模型校正环节参数，通过两个标定车速的转向盘角阶跃试验求出对应车速下汽车侧向稳态增益与1阶时间常数，在此基础上推导出任意车速下的校正环节的表达式。

1 预瞄跟随驾驶员模型

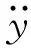
人-车闭环系统的传递函数为

W(s)=P(s)·F(s)

(1)

(2)

(3)

式中：s为拉普拉斯算子；Tp为预瞄时间；P(s)为预瞄模块；F(s)为跟随模块，包括预估环节B(s)，决策环节D(s)，校正环节C(s)和滞后环节h(s)，以及被控车辆V(s)。

本文中主要讨论校正环节C(s)参数的确定方法。对于校正环节C(s)，文献[7]中给出的微分形式的解析式为

C(s)=C0(1+TCs)

(4)

其中

(5)

式中：td，th为驾驶员反应滞后时间，一般取0.2和0.1s[8]。

汽车的侧向加速度对转向盘转角的传递函数可用下式描述[9]：

(6)

(7)

式中：Gay为汽车侧向加速度稳态增益；T1，T2，Ty1，Ty2等为常数。Gay，T1，Ty1为与汽车动态响应特性相关的参数。

2 校正环节参数求解方法

2.1 传统等效2自由度求解方法

由式(5)可知校正环节受汽车的侧向加速度稳态增益Gay和侧向加速度对转向盘转角响应的1阶时间常数T1，Ty1的影响。对于2自由度汽车模型，Gay，T1，Ty1等都可以由汽车前后轮的侧偏刚度、汽车质量、质心到前后轮的距离与绕z轴转动惯量等来直接确定[11]。

(8)

式中：vx为当前车速；isw为转向系角传动比；L为整车轴距；K为稳定性因数；lf，lr分别为质心到前轴、后轴的距离；kf，kr分别为前轴和后轴的侧偏刚度；m为整车质量。

但当被控对象为多自由度汽车模型或者真实车辆时，Gay，T1，Ty1很难直接求出，通常的方法将被控对象等效为一个2自由度车辆模型，计算出等效2自由度车辆模型的相关参数代入式(8)和式(5)中可求出C0和TC的值。

2.2 基于试验的参数求解方法

前面介绍了传统的采用等效2自由度法求微分校正环节的参数，由于汽车前后轴的侧偏刚度受载荷转移等的影响很难准确求出，采用等效2自由度的方法难免会带来位置跟随误差。下面介绍本文中提出的试验法准确求解任意车速的校正环节参数的方法。

通过式(5)发现计算TC时只需计算T1-Ty1，无需计算出T1和Ty1的具体值。根据文献[8]中由转向盘阶跃试验求单速度下多自由度车辆模型侧向加速度稳态增益和1阶时间常数差。

(9)

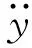
根据文献[11]中提出的方法整理出分离车速因素的侧向动力学传递函数。

(10)

其中

(11)

式中：vx为任意车速；vxt为试验车速；Gayt为试验车速下的侧向加速度稳态增益；Ty1t，Ty2t，T1t和T2t为试验车速下的传递函数各阶系数；isw为转向系等效角传动比；s为拉普拉斯算子。

(12)

(13)

利用待定系数法，通过两个不同车速vx1，vx2的转向盘角阶跃试验得到的两个车速下Gay值，求得转向系角传动比isw。

(14)

式中：Gay1，Gay2为在两个标定车速vx1和vx2的侧向加速度稳态增益值。

利用两个不同车速下求得的T1-Ty1值可求得在车速vx1下的1阶时间常数值。

(15)

式中：C1和C2分别为在两个标定车速vx1和vx2下的1阶系数差T1-Ty1值。

将式(14)和式(15)代入式(12)和式(13)求得最终需要的任意车速下侧向加速度稳态增益Gay及1阶系数T1，Ty1的表达式为

(16)

(17)

将式(16)和式(17)代入式(5)求得C0，TC关于速度的最终关系式为

(18)

3 仿真试验验证

选取CarSim中的C级样车，在Matlatb/Simulink环境下进行仿真试验分析。

3.1 标定速度确定

分别在20～140km/h每隔20km/h进行60°转向盘角阶跃试验，由式(9)得到Gay和T1-Ty1值见表1。分别取40与60km/h，40与120km/h，80与120km/h及60与100km/h 4组标定车速，从表1中查得相应的Gay和T1-Ty1值代入式(16)、式(17)得到每组车速下的计算值，与试验值的对比见图2，不同标定车速下相对误差最大值见表2。

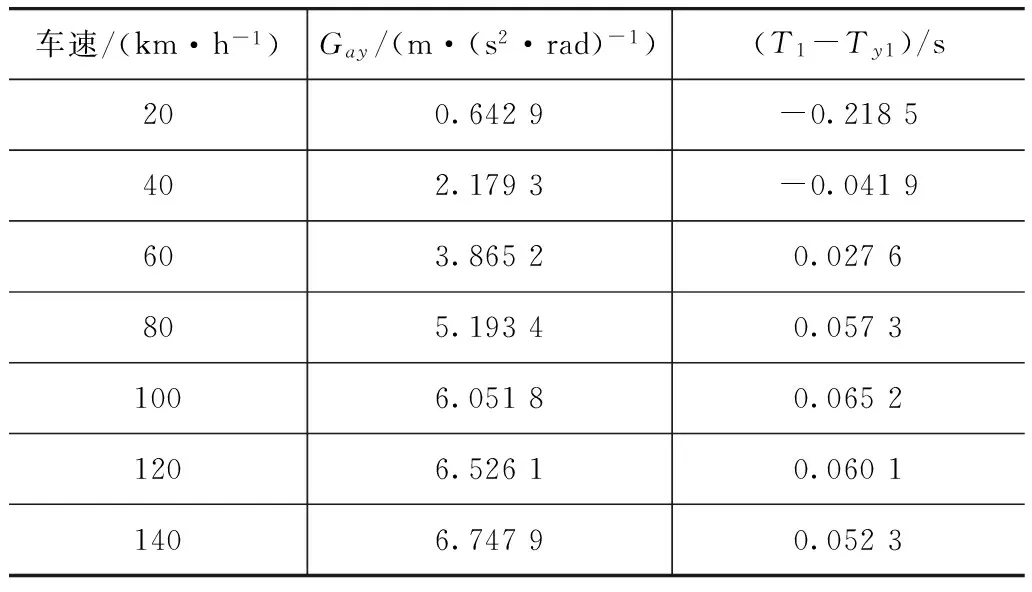
表1 Gay和T1-Ty1在各车速下的试验值

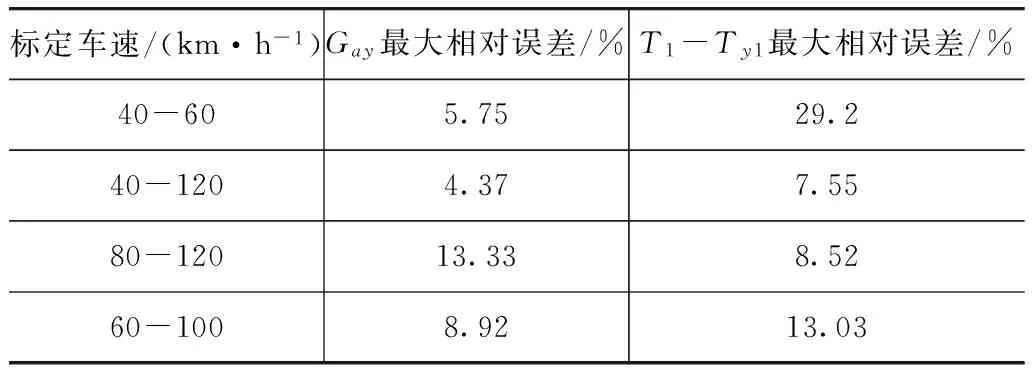
标定车速/(km·h-1)Gay最大相对误差/%T1-Ty1最大相对误差/%40-605.7529.240-1204.377.5580-12013.338.5260-1008.9213.03

由图2可知，Gay和T1-Ty1值与速度整体具有很强的非线性关系，但是当速度低于80km/h时Gay呈现较强的线性而T1-Ty1呈现很强的非线性，当速度超过80km/h时Gay呈现较强的非线性而T1-Ty1呈现很强的线性。在标定车速附近计算值与试验值间的误差较小，当标定车速选择40与60km/h时车速超过80km/h误差较大，而当标定速度选80与120km/h时，车速在20～40km/h时误差较大。由表2可知，当标定车速选为40与120km/h时误差最小，最大相对误差分别为4.37%与7.55%。

因此，选取不同车速作为标定车速求得的结果精度不同，当两个标定车速一个在低速区、一个在高速区且跨度较大时计算结果更准确。

3.2 双移线工况仿真

以C级样车为对象，在100km/h车速下进行双移线工况闭环仿真，首先采用等效2自由度车辆模型法计算Gay和T1-Ty1值。等效2自由度法计算时需要的车辆模型参数值见表3，驾驶员模型参数见表4。将表3和表4中的参数代入式(9)得Gay值为16.314 8m/(s2·rad)，T1-Ty1值为0.031 6s，代入式(5)和式(6)得C0值0.061 3，TC值为0.331 6s。用得到的C0和TC代入PO预瞄驾驶员模型中的微分校正环节进行闭环仿真得其仿真结果见图3。由图可知，等效2自由度法确定参数的行驶轨迹对预期轨迹的跟踪误差较大。当采用传统的等效2自由度方法求微分校正环节的参数时，进行100km/h双移线工况闭环仿真，最大跟随误差为1.989m，最大转向盘转角为18.287°，最大侧向加速度为0.105 9g。

表3 等效2自由度车辆模型参数

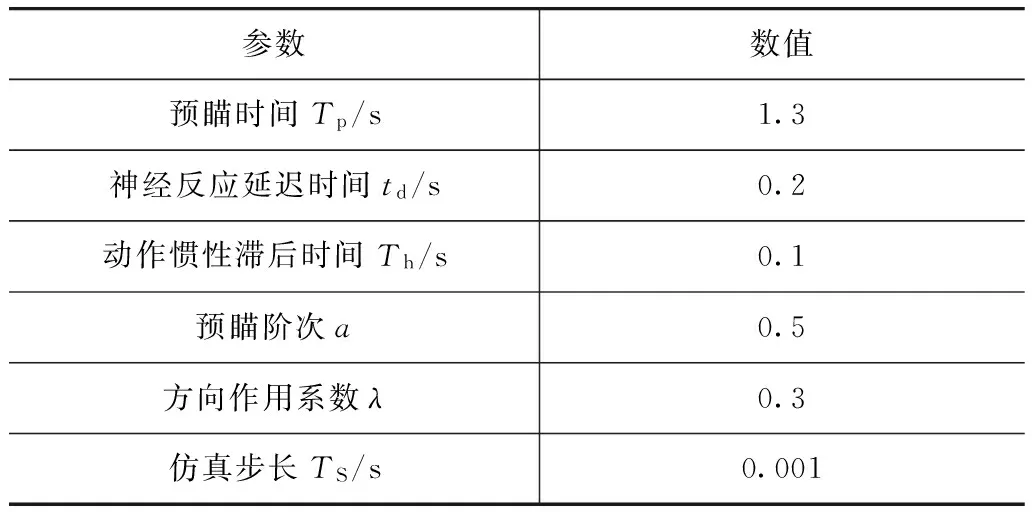
表4 驾驶员模型参数

同样以C级样车为对象，采用试验法获得微分校正环节的参数，进行双移线工况闭环仿真。由图2可得，在100km/h车速下的Gay为5.881m/(s2·rad)，(T1-Ty1)为0.059s，求得C0值为0.168 7，TC值为0.359 5s，进行双移线工况闭环仿真，结果见图4。由图可知，采用试验法求得的微分校正环节参数，最大跟随误差为0.338 41m，最大转向盘转角为12.808 5°，最大侧向加速度为0.089 4g。

同样，对速度60～120km/h间每隔10km/h分别采用等效2自由度法和试验法获得参数后进行双移线工况仿真。限于篇幅的原因，在此取两种方法进行双移线工况仿真的最大跟随误差值，见图5。

由图5可知，两种方法进行双移线工况仿真，采用试验法跟随误差较小，均在0.5m以下，而采用等效2自由度误差则较大。采用试验法求得微分校正环节参数进行仿真，其跟随性能有很大的改善，主要原因是采用等效2自由度法计算时，前轴和后轴的侧偏刚度与载荷及载荷转移等有关，但不是一个定值，导致求得的Gay和T1-Ty1与真实值相差较大。而采用试验法可以准确计算出这两个参数的值，进而准确求得微分校正环节的参数。

3.3 蛇行工况仿真

以C级样车为仿真对象，在60km/h车速下进行蛇行工况闭环仿真。

采用等效2自由度法求得在60km/h时Gay为3.734m/(s2·rad)，(T1-Ty1)为0.025 04s。进一步求得C0值为0.165 2，TC值为0.261 6s，仿真结果见图6。驾驶员其他参数见表4。在采用试验法下求得的Gay为3.734m/(s2·rad)，(T1-Ty1)为0.025 04s，得到C0值为0.258 7，TC值为0.327 6s。仿真结果如图7所示。

对速度60～120km/h间每隔10km/h分别采用等效2自由度法和试验法获得参数后进行蛇行工况仿真，取两种方法进行双移线工况仿真的最大跟随误差值如图8所示。

由图6可知，当采用传统的等效2自由度的方法求微分校正环节的参数时，进行60km/h蛇行工况闭环仿真，最大跟随误差为0.808 6m，最大转向盘转角为36.411 9°，最大侧向加速度为0.255 9g,系统对路径的跟随具有很大的跟随误差。由图7可知，采用试验法求得参数进行蛇行工况仿真，最大跟随误差为0.106 18m，转向盘转角最大值为52.356 4°，最大侧向加速度为0.365 62g。由图8可知，不同车速下采用试验法确定校正环节参数进行蛇行工况仿真，其跟随误差都要小于采用等效2自由度法，采用试验法进行蛇行工况仿真其跟随误差均在0.5m以下。人-车闭环仿真系统对蛇行工况的跟随性有显著的提高，能很好地完成蛇行工况。

4 结论

针对预瞄驾驶员模型中校正环节参数与速度具有很强的非线性难以直接求解的难点，当被控对象为多自由度车辆模型或真实车辆时很难直接给出其具体表达式等特点，提出一种基于试验数据求预瞄驾驶员模型校正环节参数的方法。在两个标定车速下进行转向盘角阶跃试验求得在这两个标定车速下的相关参数，快速外推所需参数与速度的关系，计算出各参数在不同车速下的准确值，通过试验分析可得到如下结论。

(1) 只需要进行两个特定速度下的角阶跃试验便可快速求出任意车速下Gay，T1，Ty1的值，进而求出预瞄跟随驾驶员模型中的校正环节的表达式，无需获得其他车辆参数。当被控对象为复杂的多自由度车辆模型时仍能具有很高的精确度。

(2) 选取多组车速作为标定车速进行计算，结果表明，当两个标定车速一个在低速区、一个在高速区且跨度较大时求得的表达式更准确，计算结果更接近真实试验值。

(3)采用试验法得到的校正环节参数的预瞄跟随驾驶员模型的人车闭环仿真结果表明，采用试验法求得的校正环节的驾驶员对路径具有很好的跟随特性，可以很大程度上改善跟随误差，更为准确地用于人-车闭环仿真和智能车辆控制。

[1] GUO Konghui, GUAN Hsin. Modelling of driver vehicle directional control system[J]. Vehicle System Dynamics,1993,22(3):141-184.

[2] GUZZELLA Lino, SCIARRETTA Antonio. Vehicle propulsion system[M]. Springer Berlin Heidelberg,2007.

[3] CAO J, LU H, GUO K, et al. A driver modeling based on the preview-follower theory and the jerky dynamics[J]. Mathematical Problems in Engineering,2013(4):321-324.

[4] 白艳.汽车易驾驶性评价的随机驾驶员模型[D].长春:吉林大学,2012.

[5] HUANG X C. Driver modeling and simulation based on improved preview follower algorithm[J]. Applied Mechanics & Materials,2013,321-324:847-851.

[6] 管欣,张立增,贾鑫.误差分析法求解PO预瞄驾驶员模型参数[J].汽车工程,2014,36(2).

[7] 管欣.驾驶员方向控制模型及闭环驾驶员安全性预测方法的研究[D].长春:吉林工业大学,1992.

[8] 郭孔辉.汽车操纵动力学原理[M].南京:江苏科学技术出版社,2011.

[9] BAI Yan, CROLLA D A, GUAN Hsin, et al. Linear vehicle model identification under different speed based on ARMA model[C]. SAE Paper 2012-01-0249.

[10] 唐林军.驾驶员方向控制模型的控制校正环节的研究[D].长春:吉林大学,2008.

[11] MANNING W. Vehicle handling dynamics[M]. Butterworth-Heinemann/Elsevier,2009.

The Determination Method of Parameters in CorrectionLink of Preview-Follower Driver Model

Guan Xin, Chen Yongshang, Jia Xin, Zhang Lizeng & Zhan Jun

JilinUniversity,StateKeyLaboratoryofAutomotiveSimulationandControl,Changchun130022

The accuracies of parameters in correction link of preview-follower driver model directly affect the accuracy of position control, but these parameters are hard to determine directly due to their strong nonlinear relationship with vehicle speed. Besides, for multi-DOF complex vehicle model, the simplified equivalent 2-DOF method will inevitably bring about the position following error. In this paper, a solving method of the parameters in correction link for arbitrary speed is proposed. Firstly, the related parameters for two specific speeds are calculated. Then, the relationship expression between correction parameters and speed is derived. Finally double lane change and slalom simulation tests are conducted on CarSim C class car in MATLAB/Simulink environment. The results show that the driver model with the correction parameters solved by the method proposed has better path following performance and a higher accuracy when used in human-vehicle closed-loop simulation.

vehicle; driver model; correction link; parameter determination

原稿收到日期为2015年5月14日，修改稿收到日期为2015年8月5日。