静水中大雷诺数球形颗粒变加速沉降的理论分析与试验

尹则高,王振鲁,张 黎,尹胜强

(1.中国海洋大学山东省海洋工程重点实验室,山东青岛 266100; 2.中国海洋大学工程学院,山东青岛 266100)



静水中大雷诺数球形颗粒变加速沉降的理论分析与试验

尹则高1,2,王振鲁2,张 黎2,尹胜强2

(1.中国海洋大学山东省海洋工程重点实验室,山东青岛 266100; 2.中国海洋大学工程学院,山东青岛 266100)

摘要:基于单颗粒泥沙沉降的力学机理,对静水中大雷诺数球形颗粒沉降过程中的受力状况进行分析,推导出变加速沉降运动过程的瞬时速度、沉降历时及沉降位移公式。试验数据与所推导公式的计算结果对比分析表明:计算位移与实测值相对误差都小于5%,大部分小于4%;瞬时沉速计算值与试验值相对误差都在7%以内,大部分小于5%,计算值与实测值吻合良好。

关键词:球形颗粒;变加速沉降;沉降位移;瞬时沉速;沉降历时;雷诺数

19世纪中期以来,在水力学、流体化工等领域,人们对液体中球形颗粒的沉降行为进行了大量研究。单颗粒泥沙沉降方面,Stokes[1]研究了层流中单颗粒球体的沉降现象,提出了阻力系数计算公式,该公式可用于沙粒雷诺数小于1的静水中球体的沉速规律研究。Kaplun等[2-3]采用微扰动理论得到了沉降阻力系数的公式,然而该公式同样只适用于雷诺数小于1的静水沉沙。张瑞瑾等[4]考虑颗粒黏性阻力和紊动阻力,提出了计算最终沉速的半经验公式,该公式适用于颗粒雷诺数为0. 5～1 000之间时静水中的运动。李大鸣等[5-6]研究了单颗粒球体绕流行为,提出了颗粒雷诺数小于4×104时静水中沉沙的阻力系数计算公式。Ahrens[7]引入阿基米德浮力指数,建立了估算泥沙沉速的计算公式。Smith 等[8]则采用夏威夷瓦湖岛的钙质沙粒来研究泥沙沉速,结果表明颗粒形状对最终沉速影响较大。

一般说来,群体泥沙颗粒最终沉速与单颗粒最终沉速是不同的。Han等[9]利用锥形沉降筒进行了非均匀颗粒的沉降试验,得到了相应的最终沉速公式。Winterwerp[10]研究了黏性泥沙的胶凝过程,给出了最终沉速的计算公式。Ni等[11]采用拉格朗日方法模拟了固液二相流中群体颗粒的垂直运动,结果表明颗粒间作用力和重力是影响垂向运动状态的主要因素。金文等[12]及Luo等[13]分别在长江口和太湖进行了群体泥沙最终沉速的观测。前者采用PIV(Partical Image Velocimetry)来测量平均的泥沙沉速,并分析了悬沙浓度和絮凝等因素对泥沙沉降的影响;后者的研究表明细颗粒悬浮物的最终沉速变化范围为0. 01～0. 05 cm/ s,下沉的悬浮物是以絮凝形式存在的。王筱[14]提出基于图像灰度的细颗粒泥沙群体沉速试验方法,开发了一套细颗粒泥沙沉降试验系统,通过沉降试验得到沉速随时间和颗粒浓度的变化规律,并拟合了细沙群体沉速的计算式。陈曦[15]则采用长江口的细颗粒泥沙与原状海水,利用新式沉降筒等设备,研究了悬沙静水沉速与水温、盐度、含沙量的相关关系,并给出了泥沙静水沉降的经验公式。Fathi-Moghadam等[16]模拟了湖泊以及大型水库中黏性泥沙的沉降行为,建立了絮凝率最大时最终沉速的经验方程。

目前,单颗粒球体匀速沉降的理论和公式已经被广泛地接受和应用,然而对初速度不等于最终沉速的颗粒沉降行为特性研究仍较少。初速度为零的情况下,颗粒作变加速沉降,随着瞬时沉速的增大,颗粒的有效重力和绕流阻力的合力逐渐减小,瞬时沉速继续增加,直到达到最终沉速,开始匀速沉降阶段。吴华林等[17]研究了小雷诺数静水中球形颗粒的沉降运动,建立了相应的沉速公式。本文基于泥沙沉降的力学机制的理论分析,对静水中大雷诺数的单颗粒球体的变加速沉降过程的受力情况进行了研究,给出了变加速沉降运动过程的瞬时速度、沉降历时和沉降位移公式,并通过物理模型试验,对公式计算结果与试验数据进行验证。

1 单颗粒球体静水变加速沉降的力学分析

1. 1 单颗粒球体静水变加速沉降运动方程

对一个质量为M的球形颗粒,其静水沉降的一般运动方程(坐标轴方向与重力方向一致)[17]为

式中:M、ωs、t分别为颗粒的质量、瞬时沉速和沉降时间;F为颗粒沉降所受的合力。F可以由下式[17]表示:

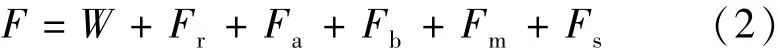
式中W、Fr、Fa、Fb、Fm、Fs分别为有效重力、阻力、附加质量力、Basset力、Magnus力以及Saffman力。式(2)最后两项统称为升力、是物体在介质中发生运动所引起的阻力,由于升力数值远小于有效重力和绕流阻力,故忽略其对颗粒沉降的影响[17];而Basset力在加速运动初期为重力的10%,在其他阶段Basset力更小,所以将该力忽略,不会给分析结果带来过大的影响[17]。因此式(2)可简化为

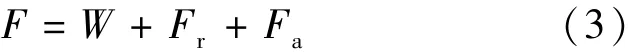
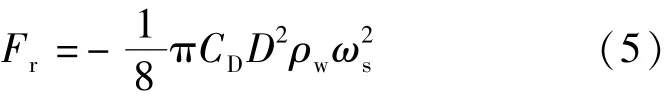
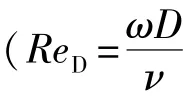
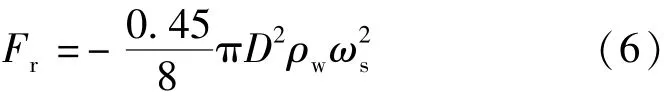
附加质量力表达的是理想流体阻碍物体非定常运动所产生的阻力,其影响表现在物体表观质量的增加量;若球形颗粒在水中做加速沉降时,增量为颗粒所排挤出的流体质量的一半。所以附加质量力可以由下式[17]表达:

式中m为与球形颗粒体积相等的水体质量。

将式(1)(4)(6)和(7)代入式(3),得到单颗粒球体在静水中的变加速沉降运动方程为

1. 2 运动方程的求解

静水中大雷诺数球形颗粒的最终沉速采用下式[18]计算:

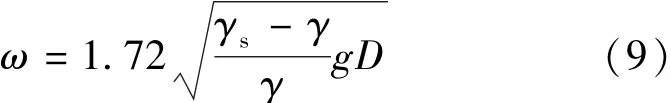
取ρw=1000 kg/ m3,令

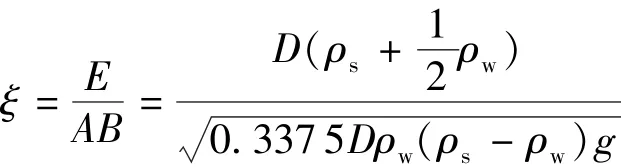
对(10)式积分得

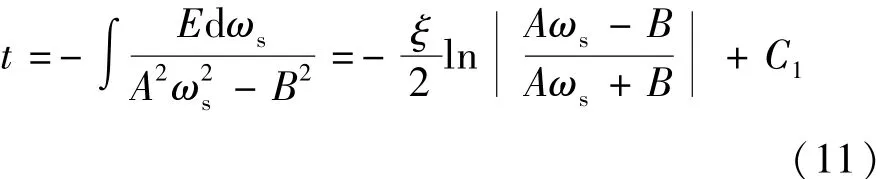
式中C1为积分常数。

式(11)可变换为

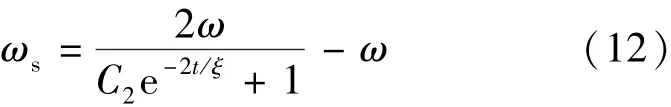
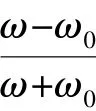
将式(13)进行变换,得到:

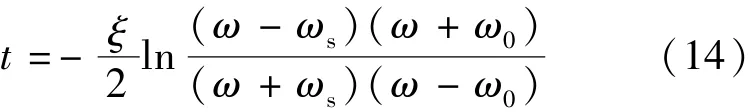
设H为变加速沉降的距离,T为时间,将dH =ωsdt对时间进行积分可得

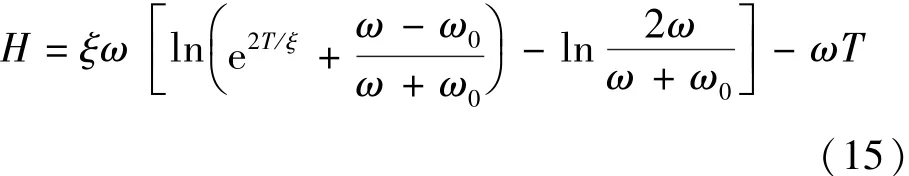
1. 3 讨论

式(13)表明,当ω0＜ω时,ωs随着时间增加而增大;当时间趋于无穷时,ωs趋于ω。当ω0＞ω时, ωs随着时间增加而减小;当时间趋于无穷时,ωs趋于ω。这反映了球形颗粒在不同的入水条件下(即初速度不同)的运动状态,其运动规律在定性上是符合实际情况的。如果将ω0=0代入式(13)(14) (15),可得

假设当ωs= 0. 9ω时,认为变加速沉降阶段结束,进入匀速沉降阶段,则变加速沉降阶段历时T和位移H为

需要注意的是,目前没有公认的判别标准来判断变加速沉降阶段的结束。如果以ωs=0. 95ω或者0. 99ω作为判别标准,会得到不同的结果。例如以ωs=0. 95ω作为结束变加速沉降阶段的判别标准,则有:

2 物理模型试验

2. 1 试验器材

长方体玻璃水槽,边长为0.3 m×0.3 m,高2 m;两种密度不同的塑料和一种玻璃球形颗粒,粒径为11.4～20.4 mm,密度分别为1 165.5 kg/ m3、1 265.2 kg/ m3和2584. 6 kg/ m3;温度计,精度为0. 1℃;摄像机、游标卡尺、刻度纸和分析天平等。

2. 2 试验步骤

第1步:测量水温和颗粒粒径、质量,计算球形颗粒的密度。按照小球密度的不同,分为3组,每组取粒径不同的4个小球,组合成12种工况,见表1。

表1 试验工况

第2步:为方便读取位移数据,在玻璃水槽外侧贴上毫米刻度纸。将球形颗粒于水面无初速度放下,自由下沉(图1),用摄像机记录球体下沉过程。由于摄像头不同的俯仰角度导致图像中颗粒在刻度纸上的位置与实际位置存在不同的偏差,试验中将摄像机分别放在不同位置(水面处、水下2 cm、4 cm、6 cm、8cm、10cm、12cm、14cm、16cm处)进行多次重复试验和观测录像,每次只读取摄像头水平位置上下2 cm范围的参数,可大致保证位置数据的准确性。从开始运动的第1帧开始,逐帧读取影像数据,找到各帧所对应的位移和时刻,计算前后两帧图像对应状态的瞬时速度。

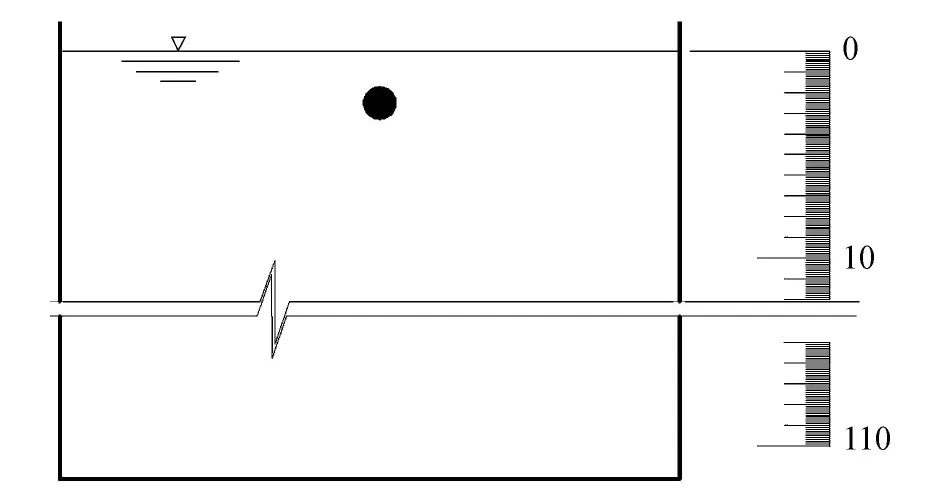
图1 沉降试验示意图(单位:cm)

第3步:在水槽外侧静水位下30cm处和110 cm处分别画上刻度线,当球形颗粒经过刻度线时,利用秒表记录对应时刻,计算匀速沉降时间,求得最终沉速。

3 数据分析与公式验证

3. 1 沉降位移

表2为变加速沉降位移的试验数据与式(20)计算结果的对比。从表1和表2可以看出,密度相等且初速度都为零的情况下,粒径越大的球形颗粒紊流区变加速沉降运动历时越长、位移越大;计算位移与实测值相比,相对误差都小于5%,一般小于4%,两者吻合较好,计算结果比较可靠。

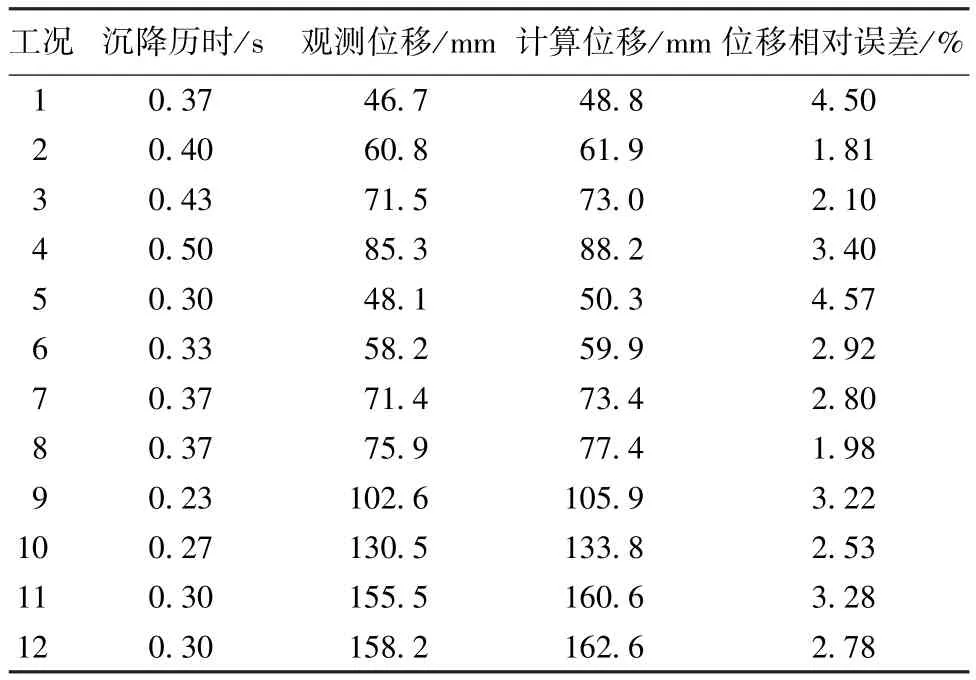
表2 实测沉降历时、位移与公式计算结果对比

3. 2 瞬时沉速

变加速运动瞬时沉速计算值和观测值的比对如图2所示(图中每两帧图像之间的时间间隔为1/30 s)。从图2可以看出,随着沉降时间增加,瞬时沉速也随之增大;随沉降时间的增加,颗粒所受合力逐渐减小,瞬时沉速增大的幅度越来越小;当瞬时沉速接近一个常数时,球形颗粒完成加速沉降并达到匀速沉降状态。图2中,瞬时沉速计算值与试验观测值相对误差都在7%以内,一般都在5%以内,相差较小,吻合较好,说明球形颗粒变加速运动瞬时沉速的计算公式比较可靠。

图2 瞬时沉速计算值与实测值对比

4 结 语

基于单颗粒泥沙沉降的力学机理,在分析静水中大雷诺数单球形颗粒受力状况的基础上,推导出变加速沉降运动过程中的瞬时沉速、沉降历时及沉降位移公式。物理模型试验结果表明,所推导公式的计算值与实测值吻合较好,推导的公式可靠,研究成果可以为球体变加速沉降运动分析提供一定的参考。

为进一步提高公式的计算精度,在后续的研究中需要适当考虑Basset力、Magnus力和Saffman力的影响。

参考文献:

[ 1 ] STOKES G G. On the effect of the internal friction of fluids in the motion of pendulums [ J]. Transactions of the Cambridge Philosophical Society,1851,9(2): 8-106.

[ 2 ] KAPLUN S,LAGERSTROM P A. Asymptotic expansions of Navier-Stokes solutions for small Reynolds numbers [J]. Journal of Mathematics and Mechanics,1957,6(3): 585-593.

[ 3 ] PROUDMAN I,PEARSON J R A. Expansions at small Reynolds numbers for the flow past a sphere and a circular cylinder[ J]. Journal of Fluid Mechanics,1957,2 (2): 237-262.

[ 4 ]张瑞瑾.河流泥沙动力学[M].第2版.北京:中国水利水电出版社,1998.

[ 5 ]李大鸣,吕小海,焦润红.泥沙静水沉降阻力系数[J].水利学报,2004,35(1): 1-5. (LI Daming,LU Xiaohai, JIAO Runhong. Resistance coefficient of sediment deposition in still water [ J ]. Journal of Hydraulic Engineering,2004,35(1): 1-5. (in Chinese))

[ 6 ] LI Daming, ZHANG Hongping, GAO Yongxiang. Series perturbations approximate solutions to N-S equations and modification to asymptotic expansion matched method[J]. Applied Mathematics and Mechanics,2002,23(8): 963-972.

[ 7 ] AHRENS J P. Simple equations to calculate fall velocity and sediment scale parameter[J]. Journal of Waterway, Port,Coastal and Ocean Engineering,2003,129(3): 146-150.

[ 8 ] SMITH D A, CHEUNG K F. Settling characteristics of calcareous sand [ J]. Journal of Hydraulic Engineering, 2003,129(6): 479-483.

[ 9 ] HAN Wenliang,GAO Guoming,WANG Guangqian,et al. Experimental study on fall velocity of non-uniform sediment in flowing water [ J]. International Journal of Sediment Research,2000,15(3): 299-306.

[10] WINTERWERP J C. On the flocculation and settling velocity of estuarine mud[J]. Continental Shelf Research, 2002,22(9): 1339-1360.

[11] NI Jinren,MENG Xiaogang. Forces on particles and their effects on vertical sediment sorting in solid-liquid twophase flows[J]. International Journal of Sediment Research,2001,16(2): 128-138.

[12]金文,王道增. PIV直接测量泥沙沉速试验研究[J].水动力学研究与进展(A辑),2005,20(1):19-23. (JIN Wen,WANG Daozeng. Direct settling velocity detection of sediment using PIV [ J ]. Chinese Journal of Hydrodynamics,2005,20(1): 19-23. (in Chinese))

[13] LUO Liancong,QIN Boqiang,GAO Guang,et al. Sediment properties and dynamics in the Taihu Lake,China[J]. International Journal of Sediment Research,2006,21(4): 312-320.

[14]王筱.非均匀细沙的沉速及水流挟沙力试验研究[D].重庆:重庆交通大学,2012.

[15]陈曦.长江口细颗粒泥沙静水沉降试验研究[D].青岛:中国海洋大学,2013.

[16] FATHI-MOGHADAM M,ARMAN A,EMAMGHOLIZADEH S,et al. Settling properties of cohesive sediments in lakes and reservoirs[J]. Journal of Waterway,Port,Coastal and Ocean Engineering,2011,137(4): 204-209.

[17]吴华林,沈焕庭,李中伟.泥沙颗粒沉降变加速运动研究[J].海洋工程,2000,18(1): 44-49. (WU Hualin, SHEN Huanting, LI Zhongwei. Acceleration motion of sediment particles in settlement process [ J ]. Ocean Engineering,2000,18(1): 44-49. (in Chinese))

[18]王昌杰.河流动力学[M].北京:人民交通出版社, 2001.

Theoretical analysis and experimental study of accelerating settlement of a spherical particle in still water with high Reynolds number

/ / YIN Zegao1,2, WANG Zhenlu2, ZHANG Li2, YIN Shengqiang2(1. Shandong Proυince Key Laboratory of Ocean Engineering, Ocean Uniυersity of China, Qingdao 266100, China; 2. College of Engineering, Ocean Uniυersity of China, Qingdao 266100, China)

Abstract:The forces on a spherical particle settling in still water with a high Reynolds number were investigated based on the settlement mechanisms of single particles of sediment. The formulas of instantaneous settlement velocity, settlement duration, and settlement displacement during accelerating settlement were deduced. The computational results from the formulas were compared with the experimental results. It was found that the relative errors were all less than 5% between the computational displacement and experimental data, and most of them were less than 4%; and the relative errors were all less than 7% between the computational instantaneous settlement velocity and experimental data, and most of them were less than 5%, indicating that the computational values agreed with the experimental data.

Key words:spherical particle; accelerating settlement; settlement displacement; instantaneous settlement velocity; duration of settlement; Reynolds number

(收稿日期:2015- 01 26 编辑:郑孝宇)

DOI:10. 3880/ j. issn. 1006 7647. 2016. 02. 002

作者简介:尹则高(1977—),男,副教授,博士,主要从事水沙动力学研究。E-mail:yinzegao@ ouc. edu. cn

基金项目:国家自然科学基金(51579229,51009123);山东省科技发展计划(2014GHY115026)

中图分类号:TV142+. 1

文献标志码:A

文章编号:1006 7647(2016)02 0006 04