流线闭口箱梁涡振气动力的雷诺数效应研究
胡传新, 赵 林, 陈海兴, 周志勇, 葛耀君
(1. 同济大学 土木工程防灾国家重点实验室,上海 200092;2. 浙江省交通规划设计研究院,杭州 310006)
涡激振动是大跨度桥梁在低风速易发的具有强迫和自激双重性质的自限幅风致振动现象。日本东京湾通道桥(Trans-Tokyo Bay Bridge)、巴西里约尼泰罗伊大桥(Rio-Niteroi Bridge)和丹麦的大带桥(Great East Belt Bridge)、美国Old Tacoma桥和中国西堠门大桥都曾观测到明显竖弯涡振[1-5]。最新研究表明,涡振发生发展过程中,气动力具有明显的演化特性[6]。雷诺数表征流体惯性力与黏性力之间的比例关系,决定了边界层的成长和流动的分离,是衡量边界层和层流向湍流转变的尺寸,对旋涡的形成具有重要影响。由于常规桥梁风洞试验无法做到雷诺数与实际结构一致,导致风洞试验预测的结构风致振动响应及静动力参数与实际结构之间存在不可忽视的差异,即为雷诺数效应。
1998年开始通车运营的丹麦大海带东桥引桥施工时,在主梁架设过程中发生涡振,实测涡振频率、涡振振幅与低速风洞试验结果不一致,由此引起各国学者对桥梁涡激共振性能受雷诺数影响问题的关注。Larsen等[7]在压力风洞中证实Strouhal数的雷诺数效应是导致风洞试验与现场实测的涡激振动起振风速不一致的原因,Schewe等[8]认为该桥梁模型的雷诺数效应是由于其尾流的拓扑结构的改变而导致的。鉴于他们的研究都是针对该特定的工程实例,研究成果具有一定的局限性,不具有普遍性,很多学者针对具体桥梁断面的涡振雷诺数效应进行了广泛研究。Larose等[9]对香港昂船洲大桥分离箱梁主梁断面进行了1∶80和1∶20高低雷诺数的试验对比研究,结果表明,0°攻角时,导流板在低雷诺数试验中会扩大涡振振幅,而在高雷诺数试验中却能大幅减小涡振振幅。张伟等[10]也针对西堠门大桥进行了高低雷诺数下分离箱梁主梁断面的涡振性能研究,发现在0°攻角下,高低雷诺数时导流板都能够大幅减小涡振振幅;攻角存在时,导流板会在低雷诺数时增加涡振振幅,在高雷诺数时减小涡振振幅,但在不同的攻角时减小幅度不同。Li等[11]也针对西堠门大桥分离箱梁主梁断面进行了涡振雷诺数效应研究,发现雷诺数越大,涡振起振风速越低,涡振最大振幅越小,涡振锁定区间越大。李加武等[12]针对流线型主梁断面进行了高低雷诺数涡振研究,发现高低雷诺数涡振锁定区间有所不同,且高雷诺数时涡振振幅大于低雷诺数时。崔欣等[13]针对某流线型闭口箱梁主梁断面进行了1∶25和1∶50高低雷诺数的试验对比研究,发现高雷诺数时涡振锁定区间及涡振振幅均远小于低雷诺数时。熊龙等[14]和杨咏漪等[15]还分别研究了挑臂式箱梁和钢桁梁主梁断面的涡振雷诺数效应。还有学者研究了雷诺数效应对桥梁断面三分力系数、表面压力系数和Strouhal数等气动参数的影响[16-19]。
综上所述,桥梁断面雷诺数效应非常复杂,不同桥梁断面对雷诺数效应的敏感程度不同[20]。风洞试验节段模型测振和测压方法是研究桥梁断面雷诺数效应的主要手段。对于分离箱梁断面,低雷诺数比高雷诺数时涡振振幅大,更为不利。而对于流线型箱梁断面,各学者得出的结论不尽一致,甚至截然相反。因而,对于流线型箱梁断面涡振雷诺数效应需要进行更为广泛而深入的研究。桥梁断面雷诺数效应的本质是不同雷诺数条件下,气流分离、再附以及尾流的拓扑结构不同。现有的研究绝大部分是针对特定的桥梁断面,不具有普遍性,较多关注宏观意义上的涡振响应,雷诺数效应对流线型闭口箱梁涡振气动力时频特性的影响研究鲜有涉及。Schewe等基于大海带东桥钢箱梁主梁断面研究发现:钢箱梁断面斯特罗哈数有明显的雷诺数效应。第一阶段,当以梁高作为特征尺寸的雷诺数Re<8×104时,斯特罗哈数为0.18;第二阶段,雷诺数Re在8×104~4×105范围内时,斯特罗哈数随雷诺数的增大而增大;第三阶段,雷诺数Re>4×105时,斯特罗哈数达到0.22,基本稳定。基于典型流线型箱梁断面,分别设计几何缩尺比为1∶70和1∶20主梁节段模型,风洞试验对应以梁高为特征尺寸雷诺数范围分别为6.08×103~2.28×104、1.06×104~1.40×105,分别对应于文献[8]主梁断面的第一阶段和第二阶段,采用风洞试验同步测振测压法,首先通过节段模型测振试验研究了雷诺数效应对主梁涡振响应影响。在此基础上,在竖向涡振区筛选典型风速点,对两种雷诺数下箱梁表面气动力时频特性进行对比研究,研究内容:分布气动力空间分布特性,包括平均风压系数和脉动风压系数;分布气动力与涡激力关系,包括分布气动力与涡激力相关性、对涡激力的贡献以及与涡激力相位差等时频特性规律。从微观层面上揭示雷诺数效应与涡振响应之间的内在联系。
1 试验概况
1.1 主梁外形
研究对象为主跨780 m斜拉桥,跨径布置为325 m+780 m+325 m。主梁断面为流线型闭口箱梁,梁宽B为38.0 m,中心处梁高D为3.1 m,主梁断面及附属设施细部,如图1所示。
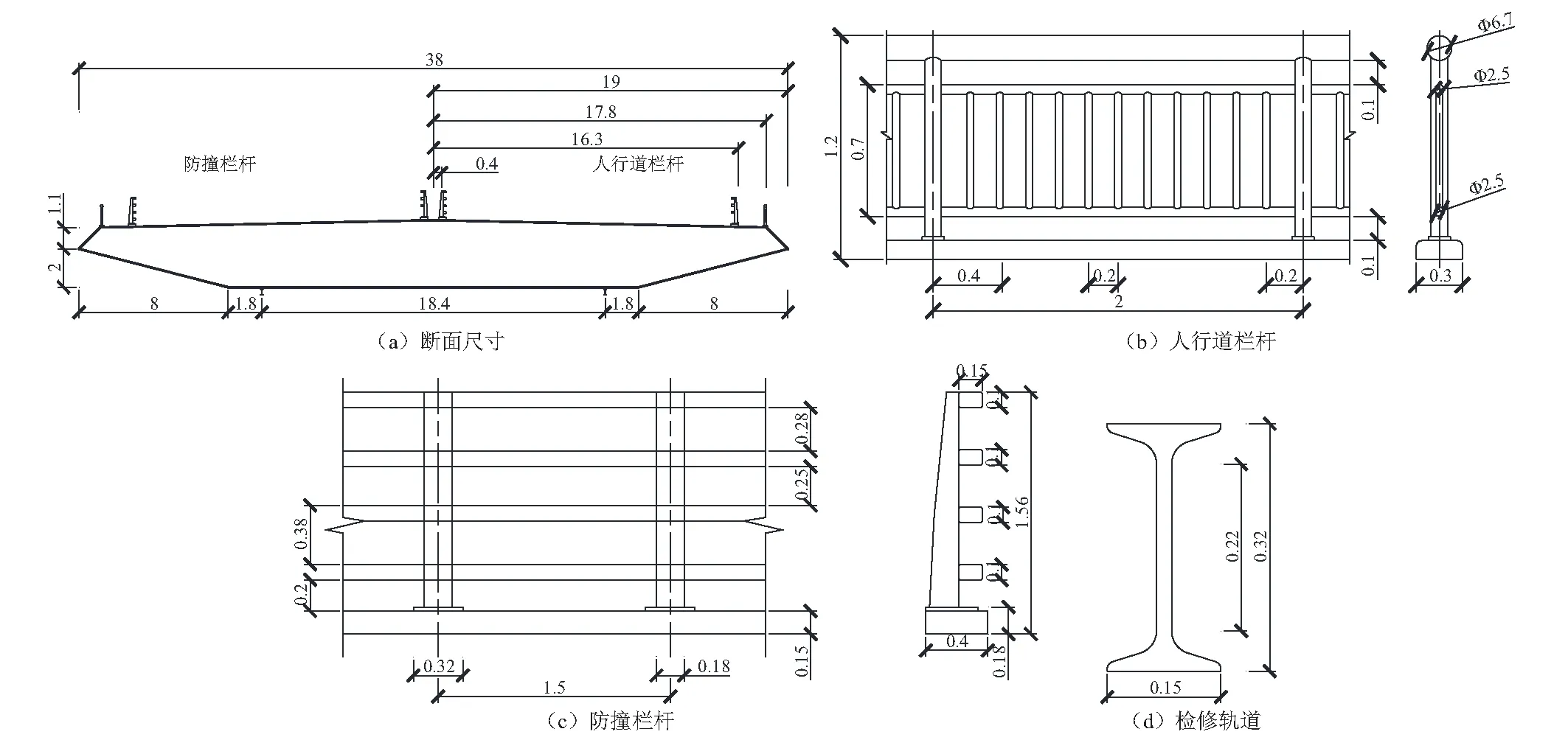
图1 主梁断面尺寸(m)
1.2 模型设计与测控设备
1∶20大比尺试验模型由钢框架提供整体刚度,防撞栏和检修轨道采用ABS板雕刻,人行道栏杆采用精加工钢管焊接,外衣采用薄钢板铺装。模型中部断面布置测压孔,共158个测点,测点间距为20~30 mm,测压管内径为0.8 mm,压力导管长度均为1 200 mm。1∶70小比尺试验模型由两根长1 700 mm,壁厚为1 mm,截面尺寸为50 mm×50 mm的薄壁空心铝方管纵梁和6个薄壁空心铝横梁构成的框架提供模型整体刚度。人行道栏杆和防撞栏均采用ABS板激光雕刻而成。模型外衣采用轻质航空木板制成,并模型中部断面布置分布式测压孔,共81个测点,测压点之间的距离在10~20 mm之间,测压管内径为0.8 mm,长度均为1 200 mm。
大比尺和小比尺节段模型分别安装于风洞内支架系统上,保证模型两端与支架系统内壁间隙足够小且在试验中不会发生接触,以避免三维绕流效应。模型与两根吊臂相连;吊臂两端再分别通过上下四根弹簧与支座系统相连,形成弹性悬挂系统,同时在吊臂处布置激光位移传感器,风洞试验如图2所示。
试验采用日本Matsushita公司MLS LM10-130 ANR1215型激光位移传感器,测量范围130±50 mm,分辨率20 μm,线性度误差在±0.2%以内。表面压力测试使用美国SCANIVALVE扫描阀公司生产的量程为±254 mm和±508 mm水柱的DSM3000电子式压力扫描阀系统、PC机和自编的信号采集软件。

图2 风洞试验
试验在同济大学TJ-3边界层风洞中进行。该风洞是一个竖向布置的闭口回流式边界层风洞,试验段长14 m,矩形断面(宽15 m,高2 m)。空风洞可控风速范围为1~17.6 m/s,连续可调,紊流度小于1%。试验过程模型及支架系统最大阻塞比小于5%,故不需对试验测量结果进行相关修正。为了减小测压信号畸变的影响,采用测压管路频响函数对测压信号进行修正。主梁节段模型的主要参数如表1所示,试验中大比尺和小比尺模型在零风速下的竖向和扭转阻尼比相同。

表1 主梁节段模型主要参数
2 试验结果与分析
对大比尺和小比尺节段模型分别进行了0°、-3°、+3°攻角下的涡激共振试验,小比尺模型试验风速为2.0~7.5 m/s,对应基于主梁特征高度的雷诺数范围为6.08×103~2.28×104。大比尺模型试验风速为1.0~13.0 m/s,对应基于主梁特征高度的雷诺数范围为1.06×104~1.40×105。0°和-3°初始攻角下,并未发现明显涡振现象。+3°初始攻角下,在不同雷诺数下涡振响应对比如图3所示。图中,横坐标表示折算风速U*=U/fhB, 其中U为来流风速,fh为竖弯频率; 纵坐标表示归一化振幅A/D, 其中A为竖向振幅。 折减风速小于2.06范围内,低雷诺数时存在2阶竖弯涡振区,不存在扭转涡振现象,高雷诺数时存在3阶竖向涡振锁定区和1阶扭转涡振区。高雷诺数时的第2阶与低雷诺数时的第1阶竖向涡振锁定区间较为接近,高雷诺数时涡振起振风速明显提前,振幅明显大于低雷诺数时;高雷诺数时的第3阶与低雷诺数时的第2阶涡振锁定区间较为接近,高雷诺数时涡振起振风速略微滞后,振幅明显大于低雷诺数时,但最大振幅发生风速基本一致。总之,与低雷诺数时相比,高雷诺数时竖向涡振发生风速低,振幅大,且出现了低雷诺数时未观测到的扭转涡振现象,故高雷诺数时较低雷诺数时更为不利,与文献[12]结论一致,与文献[13]结论相悖,进一步表明了涡振及其雷诺数效应对气动外形的敏感性。
分别取竖向涡振最大幅值对应风速点作为典型风速:大比尺模型折减风速1.99,斯托罗哈数为0.042,对应雷诺数为1.33×105,对应文献[7]中的第二阶段(斯托罗哈数随雷诺数增加而增加),以下称为高雷诺数;小比尺模型折减风速2.05,斯托罗哈数为0.041,对应雷诺数为1.89×104,对应文献[8]中的第一阶段(斯托罗哈数较小,为恒定值)以下称为低雷诺数。可知,大比尺和小比尺模型斯托罗哈数相近,与文献[21]结论相近。对上述典型风速下箱梁表面气动力进行分析,探究雷诺数效应对箱梁表面气动力时频特性影响,并揭示雷诺数效应与涡振响应之间内在联系。以下如无特别说明,均以高、低雷诺数分别指代上述风速点。

图3 不同雷诺数下涡振响应对比
3 气动力时频特性
箱梁表面压力包含了丰富的信息,可反映断面气体绕流情况,通过积分还可获得总体气动力及涡激力。根据节段模型表面压力信号,对比分析不同雷诺数时原始断面箱梁表面气动力时频特性。
3.1 分布力特性
由箱梁表面平均风压系数的分布特征可初步判断气流在结构表面的分离与再附情况。测点风压系数定义为
(1)
式中:pi(t)为i测点风压时程;U0为相应工况下来流平均风速;Cpi(t)为i测点风压系数时程。
图4给出了高低雷诺数时表面平均风压系数空间分布对比。以下为了表述方便,分别将主梁断面两风嘴尖角以上和以下区域分别称为上部区域和下部区域。图中,X/B表示无量纲坐标,B为主梁特征宽度,X为测点坐标,主梁中心处取为零。除迎风侧风嘴为正压外,其余部分处于负压区。在上表面区域,越接近迎风侧,测点区域平均风压系数越大,在下表面区域,两个检修轨道附近区域的测点平均风压系数明显高于其余部分,可能是由于检修轨道引起结构外形突变,导致气流在此区域分离,从而产生较大负压。不同雷诺数条件下,表面平均风压空间分布特性基本相似。有所不同的是,低雷诺数时上表面下游、下游上斜腹板及下斜腹板区域负压值明显大于高雷诺数。
涡振过程中,动荷载是由压力脉动部分提供,表面压力系数根方差σ反映了断面上压力脉动的强弱。图5给出了高低雷诺数时表面压力系数根方差σ空间分布对比。箱梁上表面下游、下表面下游与风嘴转角区域压力系数根方差明显较大。不同雷诺数条件下,下部区域脉动压力空间分布特性相似。有所不同的是,低雷诺数时上表面上游区域压力脉动值大于高雷诺数,上表面中游区域压力脉动值明显小于高雷诺数,而在上表面下游区域压力脉动值大于高雷诺数。特别是高雷诺数时下表面下游与风嘴转角区域压力脉动明显大于低雷诺数时。

图4 平均压力系数

图5 压力系数根方差
模型表面压力的频谱能够反映压力脉动的频率特征,卓越频率反映了压力变化主导频率,幅值谱则反映了不同频率处压力幅值。涡振时,表面压力普遍存在与涡振振动频率一致的卓越频率,表明涡振激发后,结构表面涡脱被结构振动所控制,表面气动力变化主要由卓越频率主导。定义无量纲气动力系数
(2)
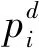
对比图5与图6可知,表面压力脉动值与卓越频率处压力幅值分布一致,表明涡振断面结构表面的压力主要以卓越频率周期性变化。与低雷诺数时不同,高雷诺数时下游检修轨道附近区域卓越频率处压力系数幅值与压力系数根方差差异较大,表明该区域压力脉动不仅有自激力成分,还含有明显的强迫力成分。
总之,不同雷诺数条件下,表面平均风压系数、压力系数根方差空间分布及压力脉动成分均有所不同,表现出显著的雷诺数效应。
3.2 分布气动力与涡激力关系
对于测压试验得到的各测点风压时程,采用压力积分的方法获取总气动力,转换到风轴坐标系后,减去均值即得涡激力时程。
箱梁表面压力与涡激力的相关性可综合反映两者的频率特征和相位特征。箱梁表面各测点所受的气动力与涡激气动力的相关系数ρi综合反映了两者的频率特征和相位特征。其定义如下
(3)
式中:ρi为i测点压力与涡激力相关系数;Faero(t)为涡激力时程;pi(t)为i测点压力时程。
图7给出了不同雷诺数时箱梁表面测点压力与涡激力相关性空间分布对比。上表面下游区域在高低雷诺数时均表现为正相关,相关系数较接近且数值在0.6以上。上表面中上游区域在高雷诺数时明显负相关,低雷诺数时相关性几乎为零。上表面中下游区域在高雷诺数时相关性为零,低雷诺数时为正相关。下表面区域在高雷诺数时表现为负相关,相关系数绝对值大于0.6,且明显大于低雷诺数时。总之,不同雷诺数时相关系数空间分布明显不同。
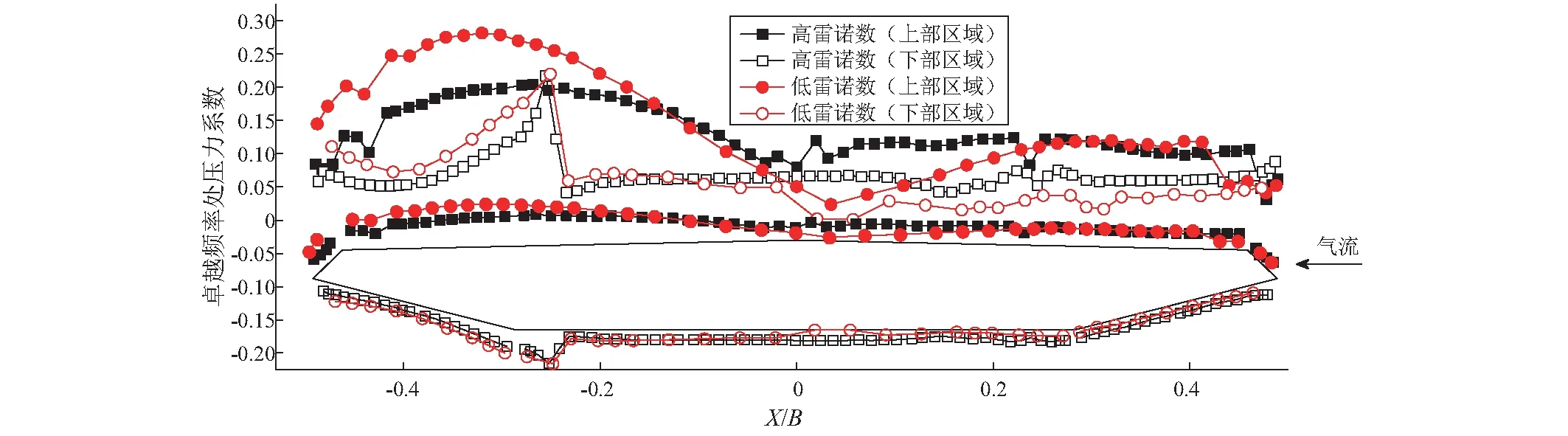
图6 表面压力卓越频率处压力系数幅值
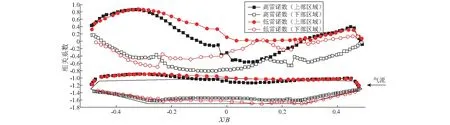
图7 表面压力与涡激力相关性
箱梁表面各测点区域分布气动力对涡振的贡献同时取决于测点压力脉动大小及其与涡激力的相关性。箱梁表面各测点区域分布气动力对涡激力贡献,可表达为
Caero-i=Cσiρi
(4)
式中:Cσi为i测点压力系数根方差;ρi为i测点压力与涡激力相关系数;Caero-i为箱梁表面各测点压力对涡激力贡献值。当Caero-i为正时,表示i测点区域分布气动力对涡激力起增强作用; 当Caero-i为负时, 表示i测点区域分布气动力对涡激力起抑制作用。
图8给出了高低雷诺数时测点区域分布气动力对涡激力贡献值空间分布对比。高雷诺数时,上表面下游、中上游和下表面区域气动力对涡激力贡献较大,其中上表面下游区域气动力对涡激力起增强作用,其它区域气动力对涡激力起抑制作用;低雷诺数与高雷诺数有所不同,上表面中上游区域气动力对涡激力几乎无贡献,上表面下游区域气动力对涡激力的贡献与高雷诺数时相近,下表面区域和迎风面斜腹板区域气动力对涡激力抑制作用远小于高雷诺数时。而下表面下游与风嘴附近区域气动力对涡激力抑制作用远大于高雷诺数时,结合第2节涡振响应对比,可推测这正是低雷诺数时涡振幅值远小于高雷诺数时的主要原因。总之,雷诺数效应引起不同区域气动力对涡激力贡献的变化,其中下表面下游与风嘴附近区域气动力对涡激力贡献作用的变化导致涡振响应的雷诺数效应。
互功率谱密度函数的相位部分即相位谱,反映了两个信号在不同频率分量上的相位差。图9给出了不同雷诺数时分布气动力与涡激力在卓越频率处相位差分布对比。上表面区域气动力与涡激力的相位差线性连续变化,在高、低雷诺数时分别在X/B=0和0.14处时产生突变。在下表面区域,高低雷诺数时相位差变化规律及数值明显不同。

图8 表面压力对涡激力的贡献
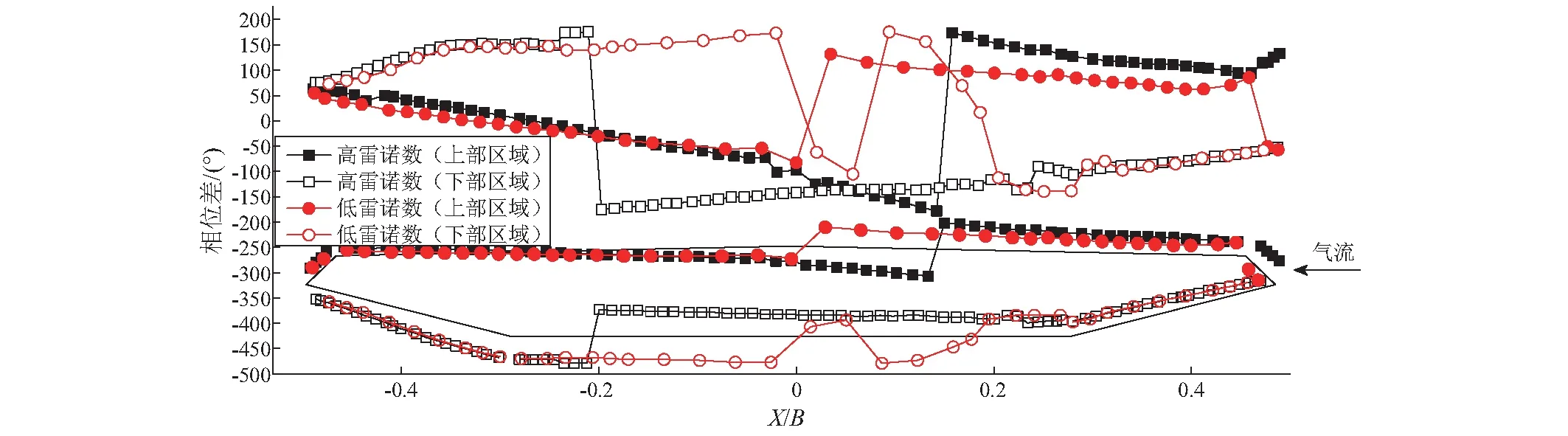
图9 分布气动力卓越频率处与涡激力相位差
总之,不同雷诺数时相位差空间分布明显不同,表现出显著雷诺数效应,该效应必然导致相关系数的雷诺数效应,由式(4)可知,进一步引起分布气动力对涡激力贡献值的雷诺数效应。低雷诺数时下表面下游与风嘴附近区域气动力对涡激力抑制作用远大于高雷诺数时,这是低雷诺数时涡振幅值远小于高雷诺数时的主要原因。故雷诺数效应引起不同区域气动力对涡激力贡献的变化,其中下表面下游与风嘴附近区域气动力对涡激力贡献作用的变化最终导致涡振响应的雷诺数效应。
4 结 论
针对典型流线闭口箱梁主梁断面,分别进行了小尺度和大尺度节段模型同步测振、测压风洞试验。涡振响应结果表明:流线型闭口箱梁断面的涡振响应具有明显的雷诺数效应,表现为高低雷诺数时涡振振幅和锁定区间均明显不同。其中,高雷诺数时较低雷诺数时更为不利,表现为涡振响应明显大于低雷诺数时,且涡振起振风速低于低雷诺数时。此外,原始断面在高雷诺数时出现了低雷诺数时并未出现的扭转涡振现象。在此基础上,在竖向涡振区筛选典型风速点,对两种雷诺数下箱梁表面气动力时频特性进行对比研究。研究结论如下:
(1) 不同雷诺数条件下,表面平均风压系数、压力系数根方差、分布气动力与整体涡激力相位差空间分布及压力脉动成分均有所不同,表现出显著的雷诺数效应。低雷诺数时上表面下游、下游上斜腹板及下斜腹板区域负压值明显大于高雷诺数。高雷诺数时下游检修轨道附近区域压力脉动明显大于低雷诺数时,且卓越频率处压力系数幅值与压力系数根方差差异较大,表明该区域压力脉动不仅有自激力成分,还含有明显的强迫力成分。上表面中上游区域在高雷诺数时明显负相关,低雷诺数时相关性几乎为零。上表面中下游区域在高雷诺数时相关性为零,低雷诺数时为正相关。下表面区域在高雷诺数时表现为负相关,相关系数绝对值大于0.6,且明显大于低雷诺数时。
(2) 高雷诺数时,上表面下游、中上游和下表面区域气动力对涡激力贡献较大,其中上表面下游区域气动力对涡激力起增强作用,其它区域气动力对涡激力起抑制作用;低雷诺数与高雷诺数有所不同,上表面中上游区域气动力对涡激力几乎无贡献,上表面下游区域气动力对涡激力的贡献与高雷诺数时相近,下表面区域和迎风面斜腹板区域气动力对涡激力抑制作用远小于高雷诺数时。而下表面下游与风嘴附近区域气动力对涡激力抑制作用远大于高雷诺数时,这正是低雷诺数时涡振幅值远小于高雷诺数时的主要原因。总之,雷诺数效应引起不同雷诺数条件下区域分布气动力对涡激力贡献的差异,其中下表面下游与风嘴附近区域气动力对涡激力贡献作用的差异是导致涡振响应雷诺数效应的主要原因。

