岩体分形离散裂隙网络系统中流体流动模拟研究进展
丁志文,董平川,李世银,谢 恩,江 杰
(1.中国石油塔里木油田分公司勘探开发研究院,新疆库尔勒 841000; 2.中国石油大学(北京)石油工程教育部重点实验室,北京 102249)
岩体分形离散裂隙网络系统中流体流动模拟研究进展
丁志文1,董平川2,李世银1,谢 恩1,江 杰1
(1.中国石油塔里木油田分公司勘探开发研究院,新疆库尔勒 841000; 2.中国石油大学(北京)石油工程教育部重点实验室,北京 102249)
摘要:回顾了岩体裂隙系统的位置、轨迹长度、方位和开度等几何拓扑结构参数的分形特征表征方法,分析了CT扫描技术对分析裂隙分形特征的重要作用,系统介绍了逾渗理论在裂隙网络系统连通性研究方面的成果,并对基于Monte-Carlo随机模拟的岩体裂隙网络系统生成方法和岩体分形离散裂隙网络系统中流体流动模拟等研究成果进行了综述。基于岩体裂隙系统的分形特征和逾渗特征建立的离散裂隙网络系统模型能够真实反映岩体裂隙的结构特征,并揭示岩体分形离散裂隙网络系统中流体流动机理,但目前尚无大型的逾渗数值模拟商业软件,分形离散裂隙网络逾渗模型算法的实现将成为研究的热点。
关键词:岩体裂隙;渗流模拟;逾渗理论;分形;CT扫描;数值模拟
裂隙多孔介质作为最为普遍的地质体,含有复杂多变的断层、裂隙、节理和层理等不连续面。在水动力学中,流体在裂隙多孔介质岩体中流动理论在油气资源的开发、地下水污染的治理、温室气体埋存和环境保护等方面得到了广泛的应用。裂隙岩体由于自身岩性特征,再加上构造、压实和岩溶等地质作用以及人类生产活动影响等,产生各种错综复杂的微裂缝和裂隙,成为地下油、气和水的重要渗流通道。目前研究裂隙多孔介质渗流的模型主要有等效连续介质模型(ECM)、离散裂缝网络模型(DFN)和混合模型(HM)。
等效连续介质模型认为裂隙岩体是一种连续介质,运用成熟的连续介质渗流理论,忽略裂隙微观水平上的裂隙结构的离散特征,用等效的渗透张量这一宏观参数来表征裂隙的渗流能力,比较经典的模型有沃伦-茹特、凯泽米和德斯旺等双重介质模型。等效连续介质模型在理论和求解上相对成熟,但该模型由流量等效确定出的等效渗透张量并不能保证流速和渗透压力的等效性,有时会掩盖裂隙的局部渗流行为[1],另外对于具体的裂隙结构,是否存在表征单元体(REV)或者表征单元体尺度是否满足远小于研究区域的尺度,这是裂隙介质是否可简化为连续多孔介质的判断标准。离散裂缝网络模型在分析裂隙的产状、开度、方位、密度、长度和连通率等微观参数的基础上,构建仿真裂缝网络,以单裂隙水流的线性立方定律或者广义达西定律为基础建立流量平衡方程,组建并求解各裂隙交叉点的流量方程组,详细刻画了每条裂隙中流体运动特征,充分考虑了裂隙非均质性、各向异性、非连续性等特点,模拟精度高;但存在裂隙特征参数的获取困难、模拟计算工作量大和适用尺度小等缺点。混合模型是基于离散裂缝网络的近似连续介质模型,其推广受限于离散裂缝网络模型的发展。
离散裂缝网络流体渗流问题一直是近年研究的热点和难点,分形理论和逾渗理论为这一复杂问题的研究提供了全新的思路,本文以离散裂缝网络模型为出发点,系统介绍裂隙结构几何拓扑空间的分形特征和裂隙网络的逾渗特征、以分形理论为依据构建裂隙网络系统模型的方法以及流体复杂的流动特征模拟方法,指出了逾渗理论对研究裂隙网络系统连通性的重要作用。
1 岩体裂隙网络系统分形特征
分形几何作为数学的一个分支,被广泛用于研究具有无标度性(scale independent)和自相似性(self-similar)特征的物体,是描述粗糙性、突变性、间断不连续的有力工具,为多孔介质孔隙结构及渗流机理提供了新思路,弥补了传统概念下的理想模型的失真性,近年来在石油工业及水利工程领域越来越受到重视。Avnir等[2]首先借助分子吸附法提出了储层岩石孔隙具有分形特征,Katz等[3-4]利用电镜扫描岩石断面,观察发现各种砂岩、页岩及碳酸盐岩在3~4个数量级(10-2~102μm)的范围内是自相似的,在2~50 μm(扫描电镜分辨率)范围内分形性质表现良好,其分形维数在2. 55~2. 87之间。有学者提出分形油藏概念,其多孔介质具有统计意义上的分形特性,此类油藏基本特征是岩石骨架、孔隙空间、孔隙表面和孔隙网络都是分形的,分形油藏模型更能客观描述具有分形结构的裂缝性低渗油藏的渗流规律[5]。岩石裂隙结构为统计意义上的分形,裂隙岩体非均质性强,特别是孔隙空间结构特征和裂隙分布是影响流体输运的主要因素之一,准确定量地描述其分布特征,建立裂隙分形维数模型,是研究裂隙岩体流体运移机理的基础。
1. 1 岩体裂隙网络系统分形维数计算方法
裂缝系统的几何特征具有分形的特征,如何确定裂缝几何参数的分形维数是建立岩体裂隙网络的关键。目前在石油工业中,计算分形维数的主要方法包括压汞法[6]、理论计算方法[7]和基于CT扫描的盒维数法[8];贺承祖等[6]根据分形理论推导了基于压汞法计算分形维数的公式,在回归的过程中,可能会出现多段直线,这是由于大孔隙和小孔隙的孔隙结构差异造成了分形维数不同;马新仿等[9]提出用分段回归方法计算孔隙结构的分形维数;赖锦等[10]分析了含水饱和度法计算分形维数会产生偏差并指出汞饱和度法的优势;Yu等[7]提出了一种计算分形维数的理论公式,并基于Sierpinski地毯严格自相似分形模型建立了分形维数的解析模型。
自20世纪80年代中后期以来,CT被用来探测岩石内部结构,Raynaud等[11]通过医用CT机对均质石膏、花岗岩、砂岩、白云岩等几种岩样断面进行扫描,得出了岩石内部裂隙;杨更社等[12-13]在国内首次应用CT检测技术对煤岩体损伤特性进行了识别,获得了对煤岩体损伤特性定性和定量的规律性认识,形成了初步的实时CT观测思路。随着计算机技术的发展,CT扫描技术发展迅速,通过岩体CT图像计算分形维数成为CT技术在岩土工程和石油工程领域的一种重要应用,CT扫描的优势在于能揭示岩石内部的孔隙拓扑结构。计盒维数(CBD)是一种在工程领域普遍应用的分形维数,计算较为简单,物理意义直观,通过计算盒子数来计算分形维数,而盒子数是统计得到的某一分形级的某一分形盒子中特定研究对象出现的次数,计盒维数就是该研究对象的分形维数。目前一般做法是将灰度CT图像转化成黑白图(二值化),然后再分析计算分形维数,但对于复杂结构的岩体,由于借助阈值分割、边缘检测等方法转化得到的黑白位图会忽略孔隙结构细节,导致后续计算的孔隙结构的分形维数偏差较大。彭瑞东等[8]直接基于灰度CT图像计算岩石孔隙分形维数,可以避免二值化过程中的干扰和误差。对于裂缝分形维数同样可以应用这一方法,彭瑞东等[14]开发了数字图像盒维数计算软件,并用于混凝土的裂纹分析,研究了裂纹分形维数与混凝土断裂韧性的关系;徐鹏等[15]借助盒维数法,对爆炸压裂模拟实验后试样产生的裂缝的分形维数进行了求解,并运用分形维数定量描述了裂缝发育情况。目前制约CT技术应用的技术瓶颈主要有两方面:一是CT图像的分辨率和成像速度;二是重构算法以及CT图像去伪影和去噪的后处理技术。
1. 2 岩体裂隙网络系统分形表征
岩体裂缝系统几何特征极其复杂,在离散裂缝网络模拟中,常常认为裂缝系统的位置、轨迹长度、方位和开度等几何参数服从统计分布规律[16],这些几何参数往往被认为是不相关的,虽然有研究[17-19]指出了裂缝的几何参数对连通性、渗透率张量和流动模式的影响,但内在的关联性并没有揭示出来。Dreuzy等[20]对裂隙空间的关联性做了深入研究,认为裂隙在所有尺度上是关联的,裂隙分布具有随机性和相关性双重特征,并且可以用分形维数来描述这种关联模式,并指出裂隙系统的连通率和渗透率会随着裂隙的相关性的增加而降低;同时还指出裂隙中心的分布显示出分形特征,通过现场观测得出对于二维模型该分形维数在1. 5~2. 0之间变化。裂隙长度是指岩体中裂隙的延伸范围,通常指沿裂隙走向或者倾向的延伸长度,通过现场测量难以得到其准确信息,由岩心或露头分析,得到的是裂缝面与界面的交线,其信息有限。但分形几何可以提供较好的模拟方法,因为裂缝长度具有分形特征,Min 等[21]通过对Sellafield区块进行野外勘查,统计分析得出裂缝长度服从幂律分布,计算得到分形维数为2. 2,并给出了裂缝长度计算公式:

式中:lmax、lmin分别为裂缝长度的最大值和最小值; D为分形维数; F为随机数,均匀分布于区间[0,1]内。
借助树脂充填、伍德合金注射、激光移位等实验技术,Johns等[22]研究得出裂缝开度服从对数正态分布,Cacas等[23-24]通过水力测试实验验证了这一分布规律。裂缝开度h的分布函数可以写成:

式中-hlog、b分别为对数正态分布函数的一阶矩和二阶矩。在裂缝开度对数正态分布图上,较大的裂缝开度值会表现出“长尾巴”形式,常常需要对数据进行截断处理,Baghbanan等[25]采取了如下的截断处理:
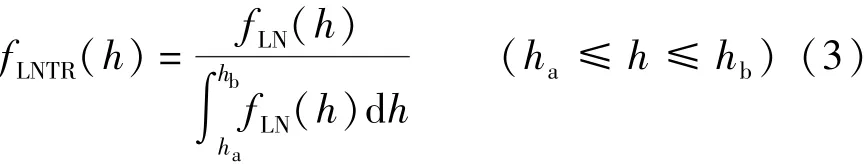
式中ha、hb分别为裂缝开度的下限值和上限值,那么大于hb或者小于ha的数据的截断分布函数值为零,有效去掉了数据噪声。裂缝开度与裂缝长度密切相关,裂缝的平均开度随着裂缝开度的增大而增大,这一关系可用h = alβ表示(a和β为回归的常数),对于简单裂缝系统β=1,即符合线性关系,但对于复杂的裂缝系统β大约为0. 5,在裂缝网络的模拟时可以充分利用这一关系。
裂缝的产状描述了裂缝的空间展布状态,通常由倾角和倾向表示。描述裂缝产状的分布函数包括Fisher分布、Bingham分布、双变量正态分布和均匀分布等,但Fisher分布具有较好的拟合效果[25],其方位的分布函数为
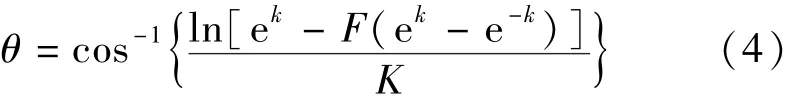
式中:K为Fisher常数;k为分布模型中的参数。因为角度数值与一般的数值不同,所以在进行裂缝产状统计时必须考虑到这种差别,利用循环统计方法可以有效避免线性统计造成的误差。
在模拟过程中,裂缝通常等效成多边形或圆形,其位置即对应的多边形或圆形的重心位置,其模拟过程通常采用泊松过程,对于二维问题,Priest[16]提出了递归随机生成方法:

式中:Ri为介于0~1之间的随机数,初始值R0可由乘积同元算法得到;int为取整函数。
裂缝的裂隙面可分为原生裂隙面和次生裂隙面,其结构和分布极为复杂,但分布规律性强,具有分形特征。光滑平直的裂隙面分形维数为2维,极端粗糙的裂隙面接近3维,实际粗糙的裂隙面维数介于这两者之间,可用分形维数来表示裂隙面的粗糙程度,裂隙面越粗糙其分形维数越大(介于2~3之间),裂隙面的形状可用随机布朗函数描述:

式中:Ck为相互独立的服从标准正态分布的随机变量;Ak、Bk为相互独立的服从均匀分布的随机变量,介于0~2之间;λ为常数,1. 0<λ<1. 5;Df为裂隙面的分形维数。
1. 3 岩体离散裂隙网络系统生成方法
岩体离散裂隙网络模型的研究始于20世纪60年代,最初的岩体离散裂隙网络模型是由3个正交方向上的等距平面组成的确定性模型。20世纪70年代Baecher等[26]开发和发展了裂缝几何地质统计模型,认识到裂缝体系几何形状与泊松过程的属性参数之间的关系,从而随机参数模型得到了初步应用;Priest等[27-28]基于无边界裂缝的假设,建立了简化泊松平面裂缝模型,该模型中裂缝任意分布,每条裂缝经过泊松过程所决定的空间点,裂缝方位由适当的概率分布确定。随后Baecher提出的圆盘模型和Veneziano提出的多边形模型是基于裂缝是有限边界的,克服了假设裂缝无边界所带来的模拟偏差,这两个模型为以后很多学者进行裂缝岩体渗流研究奠定了基础。圆盘模型假定裂缝形状为圆形或者正方形薄盘,忽略其粗糙度和起伏度,裂缝任意尺度分布,位于泊松点中心,方位任意展布,圆盘直径、产状、开度等相互独立,不能表征裂缝的簇集性质。多边形模型根据泊松过程来定义裂隙的形状和大小,泊松线将泊松面分割成多边形区域,每个区域被指定有一定的裂缝概率,裂缝轨迹长度服从指数分布,与圆盘模型的对数正态分布不同。
岩体离散裂隙网络模型的建立首先需要测量和收集裂缝特征空间分布资料,可通过地震和露头观察的方法获取大尺度的裂缝岩体资料,之后通过岩心分析获取裂隙面几何参数的概率统计模型,进而应用Monte-Carlo等随机方法生成岩体离散裂缝网络系统。分形理论对岩体离散裂隙网络骨架的构建具有重要作用,然而判断裂隙与裂隙的连通性问题则需要新的方法,逾渗理论为这一问题的解决提供了新思路。
2 岩体裂隙网络系统逾渗特征
逾渗(percolation)理论由Broadbent等[29]首次提出,最早用来研究无序多孔介质中流体的随机流动等物理行为,是处理强无序随机几何结构的重要方法之一,属于概率论的分支。分形几何方法为裂隙多孔介质的空间几何拓扑结构特征的量化表征提供了有效方法,然而对于裂隙之间的交叉和连通性分析则需要新的方法。岩体内部的多孔介质是由许多狭窄且长的孔喉和不规则的裂缝连接而成的相互连通的集团,随着外部条件而逐步演化成为贯通整个多孔介质的连通团,逾渗理论最初提出主要是为了模拟孔隙介质的随机流动,之后人们将裂隙引入到介质的逾渗研究当中,丰富了这一经典理论。可以应用裂隙网络分形几何特征,并结合Monte-Carlo等随机方法表征裂隙网络的空间架构,但是对于裂隙的连通性和渗透性的定量表征则需进一步分析,逾渗理论为这一问题的解决提供了新思路。
朱大勇等[30]应用二维座逾渗模型把岩体分成许多单元网格,建立了多单元网格渗透概率递推矩阵,并应用重整化群方法计算了基元的临界渗透概率。冯增朝等[31]基于孔隙和裂隙双重介质二维逾渗模型,分析了孔隙率、裂隙分形维数和裂隙数量分布初值等三参数与逾渗概率的关系,并提出了逾渗转变时的逾渗阀值计算表达式,揭示了孔隙和裂隙双重介质逾渗规律;吕兆兴等[32]将该模型推广到三维,编制了孔隙裂隙双重介质三维逾渗模拟软件,并发现在不同孔隙率和裂隙数量分布初值的条件下,随着裂隙分形维数的增大,必然发生逾渗转变这一现象。周波等[33]通过对尺度放大时逾渗模型中油气运移路径变化规律的模拟发现运移路径的宽度与模拟网格尺寸大小关系不大,但网格大小却与侵入相饱和度的关系密切,这个规律的发现为逾渗理论从微观尺度放大到宏观尺度提供了重要依据。
以上研究很大程度上应用的是格子逾渗(the lattice percolation)理论,国外许多学者试图应用连续逾渗(the continuum percolation)理论代替格子逾渗理论来更好地描述裂缝网络的渗透性,这就要求寻求一个合适的密度参数来等效代替格子逾渗理论中的格子占据概率,这样应用排他面积(excluded volume)概念[34]可以实现, Adler等[35]确定了无因次临界裂缝密度ρ′c(相当于逾渗阀值)为3. 6,Jafari 等[36]基于连续逾渗理论和分形几何方法,探讨了裂缝网络的分形-逾渗性质与等价裂缝渗透率之间的关系,随着ρ′-ρ′c的增大,裂缝等效渗透率增大。这一非线性增大关系在较低的逾渗阀值(ρ′c)时表现得较为明显,且裂缝密度越大渗透率越大,这一关系可表示为
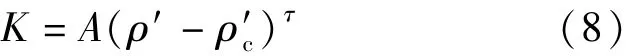
式中:K为裂缝网络等效渗透率;A为正比常数;τ为渗透率指数。Khamforoush等[37]研究了三维各向异性裂缝网络的渗透率与逾渗阀值的关系,随着各向异性的增强,x和y方向的逾渗阀值减小而z方向的逾渗阀值增大。Koudina等[38]由多边形构建了三维裂缝网络的渗透率与逾渗阀值的关系式K≈(ρ′-ρ′c)t。Sadeghnejad等[39]基于连续逾渗理论对油藏的连通性和渗透性进行了研究,将油藏分为渗透单元(比如砂岩/裂缝)和非渗透单元(比如页岩/基质),储层砂体被模拟成由多个方形网格组成,并用多个连接的砂体簇来模拟油藏的连通性,基于重整化理论用尺度放大方法模拟了油藏的有效渗透率,将逾渗理论的应用由孔隙级和岩心级扩展到了油田级。同样,万菊英等[40]应用连续逾渗理论将裂隙网络进行了简化,利用尺度放大思想将裂隙级小尺度升级到深层复杂岩体的渗透性的大尺度范围,对不同尺度下低渗储层的渗透性与无量纲裂隙密度的关系进行了研究,并用Fraca软件计算结果进行了验证,为逾渗理论应用的尺度范围提供了理论依据。
郑委等[41]基于双重逾渗模型提出了裂隙和孔隙相互构成的连通集团出现逾渗集团时的逾渗阈值函数,并研究了逾渗阀值与分形性质之间的关联性,分析了裂隙多孔介质连通性特征。自逾渗理论应用于研究裂隙网络以来,许多学者一直试图运用量化参数来判断裂隙的连通性,如Robinson[42]提出用变量^Nc=λμ2(λ为裂隙网络模型的线密度,μ为裂隙的平均长度)来判断裂隙网络的连通性;Kevin等[43]提出用变量ζ=λAμ2H(Θ)(λA为区域中裂隙的数量密度,μ为裂隙的平均长度,H(Θ)为裂隙方向分布修正系数,H(Θ)∈[0,1])来表示裂隙的连通性。
3 岩体裂隙网络系统渗流模拟
离散裂隙网络是由不同大小的裂隙个体在不同空间方向随机分布排列、相互交叉而形成的。模拟流体在裂隙中的流动,必须揭示裂隙及其交叉点上的水动力关系,体现流体在离散裂隙网络流动的非均质性和各向异性,图1给出了等效圆盘裂隙网络的渗流示意图。等效连续介质模型虽然可以直接利用经典的多孔连续介质渗流理论,但对于复杂的裂隙岩体,很难确定典型单元体的大小和等效的渗透率张量,而且也不能从本质上刻画裂隙的渗流规律。

图1 裂隙介质管状网络模型概化
目前对于离散裂隙网络渗流的模拟一般做法是:①建立裂隙网络系统的裂隙开度、间距、位置和长度的分形分布模型;②利用Monte-Carlo随机模拟方法建立裂隙网络;③根据质量守恒定律(即每个节点处的流体流出量和流入量相等),建立每个节点处的质量守恒方程,组合成裂隙网络的方程组;④应用高斯-赛德尔迭代等方法求解方程组,模拟分形裂隙系统中流体的流动过程。于青春等[44]在建立非连续裂隙网络管状渗流模型时,首先生成圆盘形三维裂隙网络,然后将该网络退化为三维空间上的管状网络(图1),假设每组裂隙内管元直径服从对数正态分布,通过优化方法确定管元直径,并结合渗流试验拟合,最终建立起稳定性强的裂隙网络管状模型。黄勇等[45]基于裂隙的走向、迹长、间距和张开度的统计特征,应用Monte-Carlo方法随机生成裂隙网络系统,依据裂隙网络交叉点处的质量守恒原理,推导了裂隙岩体网络渗流数学模型,并提出了模型的求解方法。何杨等[46]利用Monte-Carlo方法模拟岩体中裂隙网络分布情况,基于裂隙岩体网络非稳定渗流数学模型探讨了裂隙岩体中渗透水流随时间、边界条件的变化规律。冯学敏等[47]提出了反映复杂裂隙岩体渗流特性的复合单元法,这种方法也是利用Monte-Carlo方法生成裂隙网络,然后运用交切和拓扑运算将各裂隙段置于常规有限单元内部,形成由多个裂隙段划分而成的子单元的复合单元,根据推导的公式计算渗流场进而分析岩体的渗透特性;该方法考虑到了每条裂隙的位置、产状、开度、长度和渗透性质,且考虑了岩石的渗透性及其与裂隙间的流量交换,可与传统的有限元法融合且复合单元前处理简单。朱红光等[48-50]在对采动岩体流体流动研究中,探讨了裂隙的并行、串行联结等形式对裂隙网络流体流动的影响机制,并应用数值模拟方法分析了裂隙交叉流动时导致的偏流问题,基于立方定律推导了交叉联结方式的流量计算方法,研究了裂隙间交叉联结时流体的运动规律,并分析了裂隙交叉联结对岩体流体流动特性的影响机制和规律,为采动岩体真实裂隙网络系统的流体流动性质分析提供了有效手段。
Liu等[51]应用Monte-Carlo方法生成裂隙网络,并分别用分形维数DT和Df来表征流体流动的迂曲度和裂隙的几何分形特征,定量描述了岩石的渗流能力与流体迂曲度、裂缝分布和裂隙分形维的定量关系,并确定了水流沿裂缝的优势流动通道,而这些优势通道通常存在于与水流方向平行的长裂缝中,随着分形维数Df的增大,更多的较短的裂缝也能达到较大的流量并且裂缝网络中流量分布更加均匀,这一结论与Dreuzy等[17,52-53]研究的结论一致。之后Dreuzy等[54]综合分析了裂隙的分形几何拓扑结构特征,并借鉴逾渗理论表征裂缝网络等效渗透率,综合运用混合有限元方法开发了一套完整的软件(MP-FRAC)用来建立三维随机裂隙离散网络模型并模拟多种边界条件下的流体稳态流动机制,且计划尝试该模型的Monte-Carlo方法实现,在更大的三维裂缝网络对大量裂缝和边界系统进行模拟,将会大大提高流体在复杂裂隙网络系统渗流模拟的精度和效率。
4 结 语
裂隙的分形模型与传统的连续介质模型相比,更能揭示裂隙岩体流体复杂的流动和传输规律;岩体裂隙网络的分形几何拓扑结构是控制流体流动的本质因素,建立岩体裂隙网络的分形模型是研究流体流动机制的重要基础;CT扫描是揭示岩石内部孔隙拓扑结构的有效技术,将广泛而深入地应用于裂隙多孔介质微观分形拓扑结构的研究中,增大CT图像的分辨率和加快成像速度并简化重构算法是CT扫描技术以后发展的主要方向,CT扫描技术的发展可为进一步建立考虑非均质、各向异性的裂隙网络分形模型提供有力帮助。目前三维岩体离散裂隙网络模型的重构尚不够成熟,分形几何的深入应用无疑将会带来新的思路。
逾渗理论为描述复杂岩体离散裂隙网络系统微观渗流物理机制提供了新思路,能够较高效、精确地表征裂缝网络的连通性和渗透性,但是目前逾渗理论主要应用于微观尺度,其尺度的适应性需进一步研究,而且尚无大型的逾渗数值模拟软件,裂隙多重介质逾渗模型算法的实现将成为研究的热点。
参考文献:
[ 1 ]于贺,李守巨,满林涛,等.岩体分形裂隙网络系统中水流动研究进展[J].哈尔滨工业大学学报,2011(增刊1):94-99. (YU He,LI Shouju,MAN Lintao,et al. Some progress of water flow in fractal fractured rock mass[J]. Journal of Harbin Institute of Technology,2011(Sup1): 94-99. (in Chinese))
[ 2 ] AVNIR D,FARIN D,PFEIFER P. Chemistry in noninteger dimensions between two and three:Ⅱ. fractal surfaces of adsorbents[ J]. Journal of Chemical Physics, 1983, 79 (7):3566-3571.
[ 3 ] KATZ A J,THOMPSON A H. Fractal sandstone pores: implications for conductivity and pore formation [ J]. Physical Review Letters,1985,54(12):1325-1328.
[ 4 ] KROHN, CHRISTINE E. Fractal measurements of sandstones, shales, and carbonates [ J ]. Journal of Geophysical Research Atmospheres,1988,93(4):3297-3305.
[ 5 ]官庆,李允.具有分形特性的油藏渗流理论进展概述[J].西南石油大学学报,2007,29(2):106-109. (GUAN Qing, LI Yun. The application of flow through porous media of reservoir with fractal characteristic on numerical simulation[J]. Journal of Southwest Petroleum Institute, 2007,29(2):106-109. (in Chinese))
[ 6 ]贺承祖,华明琪.储层孔隙结构的分形几何描述[J].石油与天然气地质,1998,19(1):15-23. (HE Chengzu, HUA Mingqi. Fractal geometry description of reservoir pore structure[J]. Oil & Gas Geology,1998,19(1):15-23. (in Chinese))
[ 7 ] YU B,LI J. Some fractal characters of porous media[J]. Fractals,2001,9(3):365-372.
[ 8 ]彭瑞东,杨彦从,鞠杨,等.基于灰度CT图像的岩石孔隙分形维数计算[J].科学通报,2011,56(26):2256-2266. (PENG Ruidong,YANG Yangcong,JU Yang,et al. Computation of fractal dimension of rock pores based on gray CT images[J]. Chinese Science Bulletin,2011,56 (26):2256-2266. (in Chinese))
[ 9 ]马新仿,张士诚,郎兆新.用分段回归方法计算孔隙结构的分形维数[J].石油大学学报(自然科学版), 2005,28(6): 54-56. (MA Xinfang,ZHANG Shicheng, LANG Zhaoxin. Calculation of fractal dimension of pore structure by using subsection regression method [ J]. Journal of China University of Petroleum ( Edition of Natural Science),2005,28(6): 54-56. (in Chinese))
[10]赖锦,王贵文,郑懿琼,等.低渗透碎屑岩储层孔隙结构分形维数计算方法:以川中地区须家河组储层41块岩样为例[J].东北石油大学学报,2013,37(1):1-7. (LAI Jin,WANG Guiwen,ZHENG Yiqiong,et al. Method for calculation the fractal dimension of the pore structure of low permeability reservoirs:a case study on the Xujiahe formation reservoir in central Sichuan basin[J]. Journal of Northeast Petroleum University,2013,37 (1):1-7. ( in Chinese))
[11] RAYNAUD S,FABRE D,MAZEROLLE F,et al. Analysis of the internal structure of rocks and characterization of mechanical deformation by a non-destructive method:X-ray tomodensitometry[J]. Tectonophysics,1989,159(1): 149-159.
[12]杨更社,谢定义,张长庆,等.煤岩体损伤特性的CT检测[ J].力学与实践, 1996, 18 (2): 19-20. ( YANG Gengshe, XIE Dingyi, ZHANG Changqing, et al. CT detection of coal and rock damage characteristics [ J]. Mechanics and Practice, 1996, 18 ( 2 ): 19-20. ( in Chinese))
[13]杨更社,谢定义,张长庆,等.岩石损伤特性的CT识别[J].岩石力学与工程学报,1996,18(1):48-54. (YANG Gengshe, XIE Dingyi, ZHANG Changqing, et al. CT identification of rock damage properties [ J]. Chinese Journal of Rock Mechanics and Engineering, 1996, 18 (1):48-54. (in Chinese))
[14]彭瑞东,谢和平,鞠杨.二维数字图像分形维数的计算方法[J].中国矿业大学学报,2004,33 (1):19-24. (PENG Ruidong,YANG Yancong,JU Yang. Computation method of fraetal dimension for 2D digital images [ J] Journa of China University of Mining & Technology,2004, 33(1):19-24. (in Chinese))
[15]徐鹏,程远方,刘新云,等.低渗透油气藏爆炸压裂模拟试验及裂缝分形特征[J].石油勘探与开发,2013,40 (5 ): 636-640. ( XU Peng, CHENG Yuanfang, LIU Xinyun,et al. Explosive fracturing simulation experiment for low permeability reservoirs and fractal characteristics of cracks produced by explosive fracturing [ J]. Petroleum Exploration and Development,2013,40(5):636-640. (in Chinese))
[16] PRIEST S D. Discontinuity analysis for rock engineering [M]. London:Chapman & Hall,1993:473-480
[17] DREUZY,J R,DAVY P,BOUR O. Hydraulic properties of two-dimensional random fracture networks following power law distributions of length and aperture [ J ]. WaterResources Research,2002,38(12):1-9.
[18] DARCEL C, BOUR O, DAVY P, et al. Connectivity properties of two-dimensional fracture networks with stochastic fractal correlation [ J ]. Water Resources Research,2003,39(10):4307-4309.
[19] BOUR O,DAVY P. Connectivity of random fault networks following a power law fault length distribution[J]. Water Resources Research,1997,33(7):1567-1583.
[20] DREUZY J R,DARCEL C,DAVY P,et al. Influence of spatial correlation of fracture centers on the permeability of two-dimensional fracture networks following a power law length distribution[J]. Water Resources Research,2004, 40(1):62-74.
[21] MIN K B, JING L, Stephansson O. Determining the equivalent permeability tensor for fractured rock masses using a stochastic REV approach:method and application to the field data from Sellafield,UK [J]. Hydrogeology Journal,2004,12(5): 497-510.
[22] JOHNS R A, STEUDE J S, CASTANIER L M, et al. Nondestructive measurements of fracture aperture in crystalline rock cores using X ray computed tomography [J]. Journal of Geophysical Research:Solid Earth,1993, 98(2):1889-1900.
[23] CACAS M C,LEDOUX E,MARSILY G,et al. Modeling fracture flow with a stochastic discrete fracture network: calibration and validation:1. the flow model[J]. Water Resources Research,1990,26(3):479-489.
[24] BJÖRN D,JOHAN A. Application of the discrete fracture network concept with field data: possibilities of model calibration and validation[J]. Water Resources Research, 1989,25(3):540-550.
[25] BAGHBANAN A, JING L. Hydraulic properties of fractured rock masses with correlated fracture length and aperture[J]. International Journal of Rock Mechanics and Mining Sciences,2007,44(5):704-719.
[26] BAECHER G B,LANNEY N A,Einstein H H. Statistical description of rock properties and sampling [ C] / / The 18th US Symposium on Rock Mechanics ( USRMS). Golden,Colorado:American Rock Mechanics Association, 1977:1-8.
[27] PRIEST S D,HUDSON J A. Discontinuity spacings in rock [J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts,1976,13(5):135-148.
[28] HUDSON J A,PRIEST S D. Discontinuities and rock mass geometry[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1979, 16 (6):339-362.
[29] BROADBENT S R, HAMMERSLEY J M. Percolation processes[J]. Mathematical Proceedings of the Cambridge Philosophical Society,1957,53:629-641.
[30]朱大勇,范鹏贤,郭志昆,等.裂隙岩体逾渗模型中渗透概率递推矩阵[J].岩石力学与工程学报,2007,26 (2 ): 262-267. ( ZHU Dayong, FAN Pengxian, GUO Zhikun,et al. Recurrence matrix of permeable probability in percolation model for fractured rock mass[J]. Journal of Rock Mechanics and Engineering,2007,26(2):262-267. (in Chinese))
[31]冯增朝,赵阳升,吕兆兴.二维孔隙裂隙双重介质逾渗规律研究[J].物理学报,2007,56 (5):2796-2801. (FENG Zengchao,ZHAO Yangsheng,LÜ Zhaoxing. Study on percolation law of 2D porous and fractured doublemedium[J]. Acta Physica Sinica,2007,56 (5):2796-2801. (in Chinese))
[32]吕兆兴,冯增朝,赵阳升,等.孔隙裂隙双重介质的三维逾渗数值模拟研究[J].岩土力学,2007,28(增刊1): 291-294. ( LU Zhaoxing, FENG Zengchao, ZHAO Yangsheng,et al. Numerical simulation of percolation law of 3D porous and fractured double-medium[J]. Rock and Soil Mechanics,2007,28(Sup1):291-294. (in Chinese))
[33]周波,金之钧,罗晓容,等.尺度放大时逾渗模型中的油气运移路径变化规律探讨[J].石油与天然气地质, 2007,28(2): 175-180. ( ZHOU Bo, JIN Zhijun, LUO Xiaorong, et al. Changing patterns of hydrocarbon migration pathway in a up-scaling percolation model[J]. Oil & Gas Geology,2007,28(2):175-180. (in Chinese))
[34] BALBERG I,ANDERSON C H,ALEXANDER S,et al. Excluded volume and its relation to the onset of percolation[J]. Physical Review B:Condensed Matter and Materials Physics,1984,30(7):3933-3943.
[35] ADLER P M, THOVERT J F. Fracture and fracture networks[M]. Dordrecht:Springer,1999.
[36] JAFARI A, BABADAGLI T. Relationship between percolation-fractal properties and permeability of 2-D fracture networks [ J ]. International Journal of Rock Mechanics & Mining Sciences,2013,60(6):353-362.
[37] KHAMFOROUSH M,SHAMS K,THOVERT J F,et al. Permeability and percolation of anisotropic threedimensional fracture networks [ J]. Physical Review E: Statistical Physics Plasmas Fluids & Related Interdisciplinary Topics,2008,77(5):463-470.
[38] KOUDINA N, GARCIA R G, THOVERT J F, et al. Permeability of three-dimensional fracture networks[J]. Physical Review E:Statistical Physics Plasmas Fluids & Related Interdisciplinary Topics, 1998, 57 ( 4 ): 4466-4479.
[39] SADEGHNEJAD S, MASIHI M, PISHVAIE M, et al. Utilization of percolation approach to evaluate reservoir connectivity and effective permeability: a case study on North Pars gas field[J]. Scientia Iranica,2011,18(6): 1391-1396.
[40]万菊英,许鹤华,刘唐伟,等.基于逾渗方法的裂隙储层渗透性模拟[J].地球物理学进展,2014,29(3):1306-1311. (WANG Juying,XU Hehua,LIU Tangwei,et al.Simulation of fracture reservoirs permeability based on percolation method[J]. Progress in Geophysics,2014,29 (3):1306-1311. (in Chinese))
[41]郑委,鲁晓兵,刘庆杰,等.基于双重逾渗模型的裂隙多孔介质连通性研究[J].岩石力学与工程学报,2011,30 (6 ): 1289-1296. ( ZHENG Wei, LU Xiaobing, LIU Qingjie, et al. Study of connectivity of fractured porous media based on dual-percolation model [ J]. Journal of Rock Mechanics and Engineering,2011,30 (6):1289-1296. (in Chinese))
[42] ROBINSON P C. Connectivity of fracture systems-a percolation theory approach [ J]. Journal of Physics A: Mathematical & General,1983,16(3):605-614.
[43] KEVIN H,LONG J C S. Analytical expressions for the permeability of random two-dimensional Poisson fracture networks based on regular lattice percolation and equivalent media theories [ J]. Journal of Geophysical Research Solid Earth,1990,95(13):21565-21581.
[44]于青春,武雄,大西有三.非连续裂隙网络管状渗流模型及其校正[J].岩石力学与工程学报,2006,25(7): 1469-1474. ( YU Qingchun, WU Xiong, Ohnishi Yuzo. Channel model for fluid flow in discrete fracture network and its modification[J]. Journal of Rock Mechanics and Engineering,2006,25(7):1469-1474. (in Chinese))
[45]黄勇,周志芳.岩体渗流模拟的二维随机裂隙网络模型[J].河海大学学报(自然科学版),2004,32(1):91-94. (HUANG Yong, ZHOU Zhifang. 2-D stochastic fracture network model for simulation of seepage through fissured rocks[J]. Journal of Hohai University(Natural Sciences), 2004,32(1):91-94. (in Chinese))
[46]何杨,李康宏,柴军瑞.由统计规律模拟生成的岩体裂隙网络的非稳定渗流数值分析[J].应用基础与工程科学学报,2005,13(1):81-86. (HE Yang,LI Kanghong, CHAI Junrui. Numerical analysis of unsteady seepage through fracture network in rock mass simulated by the Monte-Carlo method [ J]. Journal of Basic Science and Engineering,2005,13(1):81-86. (in Chinese))
[47]冯学敏,陈胜宏.含复杂裂隙网络岩体渗流特性研究的复合单元法[J].岩石力学与工程学报,2006,25(5): 918-924. (FENG Xuemin,CHEN Shenghong. Composite element method for seepage characteristics study on rock masses with complicated fracture network[J]. Journal of Rock Mechanics and Engineering,2006,25(5):918-924. (in Chinese))
[48]朱红光,谢和平,易成,等.破断岩体裂隙的流体流动特性分析[J].岩石力学与工程学报,2013,32(4):657-663. (ZHUN Hongguang,XIE Heping,YI Cheng,et,al. Analysis of properties of fluid flow in rock fractures[J]. Journal of Rock Mechanics and Engineering, 2013, 32 (4):657-663. (in Chinese))
[49]朱红光.破断岩体裂隙的流体流动特性研究[D].北京:中国矿业大学(北京),2012:1-9.
[50]朱红光,易成,姜耀东,等.裂隙交叉联接对采动岩体中流体流动特性的影响研究[J].中国矿业大学学报, 2015,44 (1): 24-28. ( ZHUN Hongguang, YI Cheng, JIANG Yaodong,et al. Effect of fractures cross connection on fluid flow characteristics of mining-included rock[J]. Journal of China University of Mining & Technology, 2015,44(1):24-28. (in Chinese))
[51] LIU R, JIANG Y, LI B, et al. A fractal model for characterizing fluid flow in fractured rock masses based on randomly distributed rock fracture networks [ J ]. Computers & Geotechnics,2015,65:45-55.
[52] RAYNALD D, PHILIPPE D, OLIVIER B. Hydraulic properties of two-dimensional random fracture networks following a power law length distribution: 1. effective connectivity [ J]. Water Resources Research, 2001, 37 (8):2065-2078.
[53] DREUZY J R,DAVY P,BOUR O. Hydraulic properties of two-dimensional random fracture networks following a power law length distribution:2. permeability of networks based on lognormal distribution of apertures [ J]. Water Resources Research,2001,37(8),2079-2095.
[54] DREUZY J R,PICHOT G,POIRRIEZ B,et al. Synthetic benchmark for modeling flow in 3D fractured media[J]. Computers & Geosciences,2013,50(1):59-71.
Review of fluid seepage simulation in rock fractal discrete fracture network system
/ / DING Zhiwen1, DONG Pingchuan2, LI Shiyin1, XIE En1, JIANG Jie1(1. Research Institute of Petroleum Exploration and Deυelopment, Tarim Oilfield Company, PetroChina, Korla 841000, China; 2. MOE Key Laboratory of Petroleum Engineering, China Uniυersity of Petroleum, Beijing 102249, China)
Abstract:Methods for description of fractal characteristics of geometric topological parameters of a rock fracture network system, including the length, aperture, orientation, and location, are reviewed. Percolation characteristics in the rock fracture network system and the important role of CT scanning technology in analyzing the fractal characteristic of fractures are pointed out. Achievements in research on the connectivity of the fracture network system using the percolation theory, methods for generation of the rock fracture network system based on the Monte-Carlo method, and simulation of fluid seepage in a fractal discrete fracture network system are systematically introduced. It is concluded that a model of the rock fractal discrete fracture network system constructed based on fractal characteristics and percolation characteristics can reflect the real rock fracture structure and seepage mechanism in the fracture network system. However, there is no large-scale commercial software for numerical simulation of percolation at present. Construction of a numerical model for the fractal discrete fracture network system based on the percolation theory will become the major research focus.
Key words:rock fracture; seepage modelling; percolation theory; fractal; CT scanning; numerical simulation
(收稿日期:2015- 04 14 编辑:熊水斌)
作者简介:丁志文(1988—),男,助理工程师,硕士,主要从事油藏数值模拟研究。E-mai:ding_zhiwen@126. com
基金项目:国家自然科学基金(50574059,50004002)
DOI:10. 3880/ j. issn. 1006- 7647. 2016. 02. 016
中图分类号:P641. 135
文献标志码:A
文章编号:1006- 7647(2016)02- 0087- 08

