一种改进的调合辛烷值模型预测汽油研究法辛烷值

张玉瑞，陈微微，周晓龙，肖云鹏

(1.华东理工大学石油加工研究所，上海 200237；2.中国石化安庆分公司)

一种改进的调合辛烷值模型预测汽油研究法辛烷值

张玉瑞1，陈微微1，周晓龙1，肖云鹏2

(1.华东理工大学石油加工研究所，上海 200237；2.中国石化安庆分公司)

对中国石化安庆分公司(安庆石化)汽油调合组分油进行调合实验，建立了修正的调合辛烷值模型预测汽油的研究法辛烷值，利用基于LM改进的信赖域方法进行了模型非线型回归。选取安庆石化实际生产数据验证模型准确性，比较了线性模型、调合辛烷值模型、改进调合辛烷值模型的预测效果。通过对比3种模型的预测结果，发现3种模型中改进调合辛烷值模型具有较好的预测效果，平均绝对误差0.49，平均相对误差0.5%，残差均方和是0.74，模型的R2是1.08。

汽油调合 研究法辛烷值 预测模型 信赖域方法

汽油调合是车用汽油生产的关键步骤。传统的罐装调合工艺油罐较多，占地面积大，并且调合多依赖经验，辛烷值过剩较大，容易造成经济损失。近年来，炼油厂纷纷改进工艺，引进先进的汽油在线调合工艺，因此准确的石油品质预测模型成了改进技术的重点[1-2]。

辛烷值是汽油最主要的品质指标。辛烷值与汽油组分密切相关[3]，调合组分之间存在相互作用，因此辛烷值预测模型表现为非线性。Rusin等[4]提出转换模型，认为非线性主要是由灵敏度、汽油组分(芳烃、烯烃、烷烃)之间的相互作用以及提高汽油辛烷值的添加剂引起的。Healy[5]提出了Ethyl模型，分析了调合汽油组分的辛烷值水平、烯烃和芳烃含量对调合辛烷值的影响，并且引入调合组分的敏感性，得出调合汽油的辛烷值。Twu等[6]为确保模型能描述整个组成范围内相同或不同组分的调合行为，并且可用于多组分调合物的预测，提出二次非线性调合模型。Pasadakis等[7]利用神经网络模型预测调合汽油辛烷值，以调合组分的体积比率和辛烷值作为神经网络输入，调合汽油的辛烷值作为神经网络输出。Ghosh[8]基于汽油中具体组分建立模型，认为辛烷值的贡献是由组分调合辛烷值以及组分之间相互作用两部分共同作用的结果。Foong等[9]提出一种含有乙醇抗爆剂的调合成品油的预测模型，通过乙醇和未添加乙醇的调合油的摩尔加和的方式预测最终油品的辛烷值，偏差较体积加和小。由于辛烷值与分子结构密切相关，Andreas[10]利用近红外光谱结合多元线性回归的方式预测油品的辛烷值，精度较高；Meusinger等[11]利用13C NMR和神经网络结合的方式预测分子的辛烷值；Smolenskii等[12]通过建立分子拓扑结构，进而通过回归方法建立模型预测分子的辛烷值。陈新志[13]提出的虚拟纯组分模型，将各种汽油组分视为虚拟的纯组分，采用基于局部组成概念建立辛烷值模型。薛美盛等[14]提出汽油调合指数模型，该模型是将调合组分油的实际辛烷值进行指数变换，得到计算辛烷值后进行线性加和得到成品油的计算辛烷值，具有易线性化的特点。

本研究通过对中国石化安庆分公司(安庆石化)调合油品进行辛烷值调合特性的实验研究，建立改进的调合辛烷值模型；比较线性模型，调合辛烷值模型以及改进的调合辛烷值模型之间的差异。采用信赖域方法(改进的LM法)对模型进行非线性回归，并使用安庆石化实测生产数据验证模型的准确性。

1 模型建立

一般认为辛烷值的非线性主要由两方面引起：一是组分的灵敏度(不同测试条件下引起的辛烷值的差异)；二是组分之间的相互作用。

1.1 灵敏度影响

同种燃料在不同的测试条件(压缩比、转速、进气温度等)下表现出不同的抗爆性，例如用辛烷值为90的某组分油来调合93号或97号成品油时，由于测试两种成品油辛烷值时压缩比不同，此组分油在两种成品油中表现出的调合辛烷值不同。Ghosh等[8]通过实验发现不同分子的调合辛烷值和调合用油品的辛烷值成线性相关，具体如下：

ON=∑xi×BiON

(1)

BiON=a0+a1×ON

(2)

当只有一种物质时，BiON=ON=ONi，因此公式(2)化简为

ONi=a0i+a1i×ONi

(3)

所以

a0i=(1-a1i)×ONi

(4)

假设1-a1i=bi；公式(4)变为

a0i=bi×ONi

(5)

带入(2)和(1)式，最终得到

ON=(∑xi×bi×ONi)(∑xi×bi)

(6)

式中：ON为油品辛烷值;BiON为纯物质的调合辛烷值；ONi为纯物质的辛烷值；a0，a1，a0i，a1i，bi为参数；xi为组分体积分率。

上述模型需要知道汽油中所有的分子或者某些相似分子组成的集总，而汽油是一个复杂的大量分子组成的超级混合物，因此比较繁琐。在此，把汽油的调合组分作为一个纯组分参与调合，大大减少了集总的数目。即存在几个调合组分就存在几种集总，而集总的参数bi代表集总内物质相互作用的结果。

1.2 组分的相互作用影响

不同的物质之间的相互作用是不同的，主要有下述规律[3]：①同族物质调合时辛烷值和组成表现为线性相关，例如主要由饱和烃构成的组分油A和B，A和B调合的油品辛烷值大致等于体积线性加和值；②烯烃和饱和烃之间表现正偏差；③芳烃和不同浓度的烯烃表现轻微的负偏差，芳烃和饱和烃之间表现正偏差。利用式(7)表示二元调合中组分之间相互作用引起的偏差：

Deviation=CφAφB(1+KφA)

(7)

式中：φA和φB分别代表二元调合组分的体积分数；B为易产生爆震的物质；A为不易产生爆震的物质或者一定程度上阻止物质B爆震的物质；C和K为模型参数。Rusin等[4]利用族组成集总的方式按照此种方法(式7)表示汽油中物质之间相互作用引起的非线性，得到较好的预测结果。采用类似的方法，将汽油进行集总，分为芳烃、烯烃和饱和烃，通过式(7)表示物质之间的相互作用对辛烷值的贡献。

1.3 模型的整合

通过上述分析和假设，得到汽油辛烷值非线性的两方面影响模型(6)和(7)，通过整合得到：

RON=(∑xi×bi×ONi)(∑xi×bi)+Dev

(8)

Dev=C1VAVP(1+K1VA)+C2VOVP(1+K2VO)+

C3VAVO(1+K3VA)

(9)

式中：VA，VP，VO分别为成品汽油中芳烃、饱和烃、烯烃的体积分数；bi，C1～C3，K1～K3为模型参数。

辛烷值模型一般满足下列事实：①两个相同的组分油调合或者单独的组分油和自身调合时，辛烷值等于组分油的辛烷值；②调合汽油的辛烷值不应受到调合顺序的影响。

模型(8)显然不符合第一点事实，其主要原因是式(8)中前半部分ONi包含了其本身内部组分之间的相互作用，然而在后面的部分Dev中又一次出现，造成了与事实(1)不同的结论。对式(8)引进修正因子ri进行修正，修正如下：

RON=[∑xi×bi×(ONi-ri)](∑xi×bi)+Dev

(10)

Dev=C1VAVP(1+K1VA)+C2VOVP(1+K2VO)+

C3VAVO(1+K3VA)

(11)

ri=C1V′AV′P(1+K1VA)

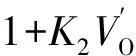
(12)式中：V′A，V′P，V′O分别为调合组分油的芳烃、饱和烃、烯烃体积分数；bi，C1～C3，K1～K3为模型参数。

针对不同的调合组分油，ri可以作相应的简化，例如对于重整油，油品主要是芳烃和饱和烃组成，所以芳烃和烯烃，烯烃和饱和烃的相互作用项就可以忽略。而对于主要含有饱和烃的拔头油或者抽余油可以将ri忽略。

2 实 验

2.1 实验方案

(1) 实验所用原料均来自安庆石化，首先对组分油进行实验分析，主要测量研究法辛烷值、族组成(芳烃、烯烃、饱和烃的体积分数)。

(2) 进行组分油配比实验，测量调合后油品的研究法辛烷值、族组成。用于模型回归的配比实验共进行38组。

(3) 通过实验数据进行模型参数回归求解。

(4) 实际生产数据验证模型的准确性。

2.2 实验数据

分别对30组不同时间生产的组分油进行实验分析，发现组分性质变化不大。其中，拔头油和抽余油轻组分较多，辛烷值测试不准确，采用经验数据,部分数据见表1。由于组分性质变化不大，采用平均值作为最终组分油的各性质数据，见表2。

表1 组分油性质数据

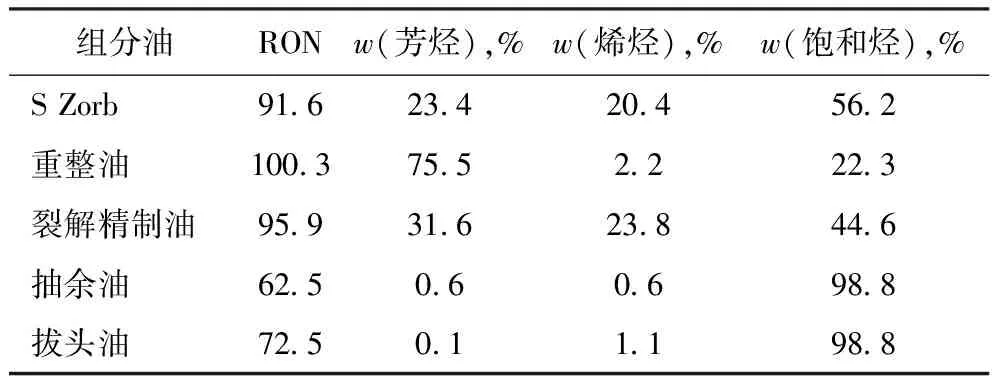
表2 各组分油数据

表3是进行配比实验的部分数据。另外随机选取31组安庆石化2015年1—7月的生产数据进行模型验证。

表3 汽油配方以及配方的辛烷值

3 模型计算

利用实验数据拟合模型参数。线性模型进行线性回归，调合辛烷值和改进的调合辛烷值由于是非线性模型，采用信赖域法进行非线性回归，以上所有的回归程序是在Matlab环境实现的。

3.1 线性模型

RON=∑xi×ONi

(13)

利用安庆石化实际生产数据验证模型准确性，预测结果分析如下：最大绝对误差3.43，平均绝对误差1.33，平均相对误差1.4%，残差均方和为1.7，模型的R2为3.23，偏差较大。

3.2 调合辛烷值模型

RON=(∑xi×bi×ONi)(∑xi×bi)

(14)

利用信赖域方法进行非线性拟合求得模型参数，结果见表4。

表4 调合辛烷值模型参数

利用安庆石化实际生产数据验证模型准确性，对预测数据进行残差分析，结果见图1。基线表示实际生产数据，红色圆圈表示预测数值，圆圈与基线的垂直距离表示残差，垂直的黑实线代表残差的信任区间，置信水平0.05。从图1可以看出，大部分数据偏差在±1之间，并且多数在信任区间中，残差信任区间均通过0处位置，最大绝对偏差出现在第三组，最大偏差是1.99，平均绝对误差0.57，平均相对误差0.6%，残差均方和为0.88，模型的R2为0.909，可见模型的拟合效果较好。

图1 预测数据的残差分析○—预测值； —实际生产数据; ┃—置信水平为0.05的残差置信区间。 图2同

3.3 改进的调合辛烷值模型

改进辛烷值模型具体形式见式(9)～式(11)。对于抽余油和拔头油忽略ri的影响，对于重整油只考虑ri中芳烃和饱和烃的影响，对于热裂解和S Zorb油采用ri形式。

利用信赖域方法进行非线性拟合求得模型参数，结果见表5。

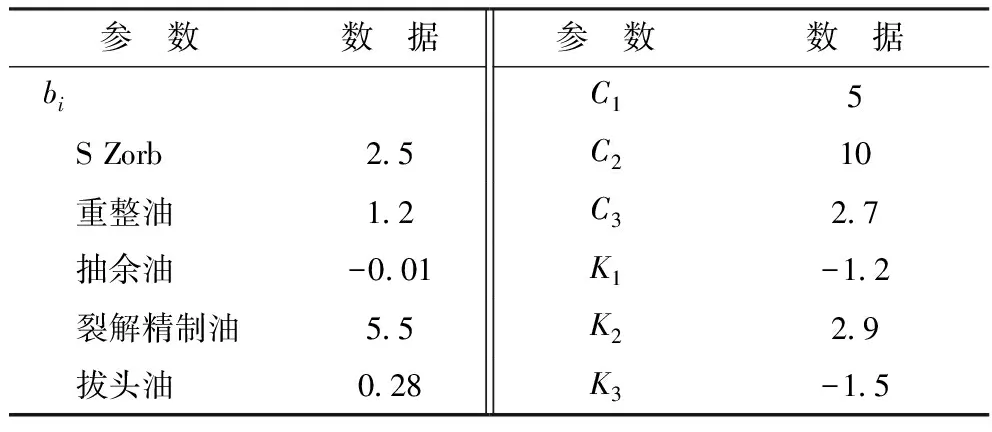
表5 改进调合辛烷值模型参数

利用安庆石化实际生产数据验证模型准确性，对预测数据进行残差分析，结果见图2。从图2可知，多数数据在残差的信任区间内，信任区间均通过0处位置，最大绝对偏差出现在第三组，最大偏差是1.94，平均绝对误差0.49，平均相对误差0.5%，残差均方和为0.74，模型的R2为1.08，模型优于调合辛烷值方法。

图2 预测数据的残差分析

图3表示线性模型、调合辛烷值模型、改进调合辛烷值模型的预测数据和实际生产数据的关系。从图3可以看出：线性模型偏差较大，调合辛烷值基本和实测数值相近，改进的调合辛烷值虽然也存在一定偏差，但预测效果优于调合辛烷值方法；最大偏差大概出现在同一位置，通过对比配方，发现偏差较大的点配方和相似配方的辛烷值相差较大，因此推断此处偏差应该是由测量误差引起。

图3 实测辛烷值和模型预测辛烷值对比■—实测数据； ●—线性模型预测数据； ▲—调合辛烷值模型预测数据；—改进调合辛烷值模型预测数据

4 结 论

(1) 通过拟合计算，线性模型的偏差较大，最大绝对误差3.43，平均绝对误差1.33，平均相对误差1.4%，残差均方和为1.7，模型的R2为3.23；调合辛烷值模型最大偏差为1.99，平均绝对误差0.57，平均相对误差0.6%，残差均方和为0.88，模型的R2为0.909；改进的调合辛烷值模型最大偏差是1.94，平均绝对误差0.49，平均相对误差0.5%，残差均方和为0.74，模型的R2为1.08。对比发现，改进辛烷值模型方法具有可行性。

(2) 通过对比线性模型和调合辛烷值模型发现，测试条件的改变是辛烷值预测非线性的一方面原因；对比调合辛烷值模型和改进调合辛烷值模型，可以认为组分相互作用是非线性产生的另一方面原因，证实了模型建立的正确性。

[1] 王伟.基于油品性质的汽油调合辛烷值模型的选取[J].石油学报(石油加工)，2006，22(6)：39-44

[2] 黄凤林.调合汽油辛烷值模型[J].西安石油学院学报，1999，14(5)：54-57

[3] 彭朴，陆婉珍.汽油辛烷值和组成的关系[J].石油炼制与化工，1981，12(6)：27-38

[4] Rusin M H，Chung H S，Marshall J F.A “Transformation” method for calculating the research and motor octane number of gasoline blends[J].Industrial and Engineering Chemistry Fundamentals，1981，20(3)：195-204

[5] Healy.Predicting motor and distribution octane numbers of multi-component blends[J].Journal of The Japan Petroleum Institute，1975，18(3)：193-195

[6] Twu C H，Coon J E.Predict octane numbers using a generalized interaction method[J].Hydrocarbon Processing，1996，75(2)：51-56

[7] Pasadakis N，Gaganis V，Foteinopoulos C.Octane number prediction for gasoline blends[J].Fuel Processing Technology，2006，87(6)：505-509

[8] Ghosh P，Hickey K J，Jaffe S B.Development of a detailed gasoline composition-based octane model[J].Ind Eng Chem Res，2006，45(1)：337-345

[9] Foong T M，Kai J M，Brear M J，et al.The octane numbers of ethanol blended with gasoline and its surrogates[J].Fuel，2014，115(1)：727-739

[10]Andreas A.Autoregressive modeling of near-IR spectra and MLR to predict RON values of gasoline[J].Fuel，2010，89(1)：158-161

[11]Meusinger R，Moros R.Determination of octane numbers of gasoline compounds from their chemical structure by13C NMR spectroscopy and neural networks[J].Fuel，2001，80(5)：613-621

[12]Smolenskii E A，Ryzhov A N，Bavykin V M，et al.Octane numbers(ONs)of hydrocarbons：A QSPR study using optimal topological indices for the topological equivalents of the ONs[J].Russ Chem Bull Int Ed，2007，56(9)：1681-1693

[13]陈新志.调合汽油研究法辛烷值模型的建立[J].石油炼制与化工，1997，28(1)：52-55

[14]薛美盛，李祖奎，吴刚，等.成品油调合调度优化模型及其应用[J].石油炼制与化工，2005，36(3)：65-68

RON PREDICTION BY IMPROVED MODEL FOR BLENDED GASOLINE

ZhangYurui1， Chen Weiwei1， Zhou Xiaolong1， Xiao Yunpeng2

(1.ResearchInstituteofPetroleumProcessing，EastChinaUniversityofScienceandTechnology，Shanghai200237；2.SINOPECAnqingCompany)

Based on the blending experiments of gasoline blending components(from Anqing branch)and the model parameters calculated by non-linear regression LM trust region method， an improved RON prediction model was established. The accuracies for RON prediction was tested and compared for linear model， blending model and improved blending model using real data of the production. The results of the improved model are： mean absolute error of 0.49， average relative error of 0.5%， MSE of 0.74， andR2of 1.08， indicating the better prediction effect of the improved blending model than the other two models.

gasoline blending； RON； predicting model； trust region method

2015-10-13； 修改稿收到日期： 2016-01-04。

张玉瑞，硕士研究生，主要研究方向为汽油调合模型的建立。

周晓龙，E-mail：xiaolong@ecust.edu.cn。

参加工作的还有华东理工大学石油加工研究所的宋月芹和中国石化安庆分公司的产圣。