基于区间中智集的ELECTRE方法及其在多属性决策中的应用

刘培德，李洪刚，王 鹏，刘俊麟

（1.山东财经大学管理科学与工程学院，山东济南 250014；2.中国民航大学经济与管理学院，天津 300300）



基于区间中智集的ELECTRE方法及其在多属性决策中的应用

刘培德1，2，李洪刚1，王 鹏1，刘俊麟1

（1.山东财经大学管理科学与工程学院，山东济南 250014；2.中国民航大学经济与管理学院，天津 300300）

摘 要：针对多属性决策中信息的不确定性，不完全性和不一致性，考虑到不同数据类型的可能度问题，文章提出了基于区间中智数的ELECTRE方法。首先介绍了区间中智集和可能度，然后针对传统的以实数表示评价信息的ELECTRE方法的不足，将ELECTRE方法与区间中智数相结合提出一个扩展的ELECTRE方法，在方案属性值用区间中智数表示的基础上，计算每个方案相对于其他方案的相对优先度和相对劣势度，并根据净优势度对方案进行排序。最后用一个实例验证该方法的可行性和有效性。

关键词：区间中智数；ELECTRE方法；多属性决策

0 引 言

多属性决策问题被广泛应用于政治、经济、文化等领域［1 -3］，成为当今研究的重点。通常情况下，在多属性决策中决策信息是不确定、不完全和不一致的。传统的模糊集［4］只考虑了隶属度而忽视了非隶属度的重要性，虽然之后提出的直觉模糊集［5］和区间直觉模糊集［6 -7］将非隶属度补充到了模糊集中，但他们还是只能处理不完全的信息，不能处理不确定、不一致的信息。为了更加全面地处理各种信息，Smarandache［8］提出了中智数理论。中智数考虑了直觉模糊数所忽视的犹豫度，所以，中智数较之直觉模糊数更加适合处理不确定信息。但是，单值的中智集［9］用实数去表示隶属度、非隶属度和犹豫度，还不能更好地表示信息的模糊性，因此，Wang等［10］提出了区间中智集，用区间数表示隶属度、非隶属度和犹豫度，这使得评价结果更为可靠。

到目前为止，已经有了很多的多属性决策方法，TOPISIS、VIKOR、PROMETHEE、灰色关联度、灰色投影等［11 -15］。ELECTRE方法，首先由Benavoun，Roy与Sussman于20世纪60年代提出，随后很多人将其进一步发展，相继提出ELECTRER I法、ELECTRE II法和ELECTRE III法［16］。这些方法大多针对的决策数据是明确数据，为了更好地应用于实际问题，刘培德［17］提出了基于语言变量改进的ELECTRE方法，吴彩虹等［18］进一步提出了针对区间数的改进的ELECTRE方法，Wan等［19］则将ELECTRE方法所需要的可能度扩展到区间直觉模糊数，也就是用模糊数去描述决策信息，使得更模糊更复杂的数据有了更好更简单的处理方法。无论是实数还是模糊数在描述模糊决策信息方面都不如区间中智数，区间中智数可以通过隶属度、犹豫度和非隶属度来表示专家对评价方案的肯定度、不确定度和否定度，用区间数表示隶属度、犹豫度和非隶属度能使评价结果更准确。基于区间中智数的优点，本文将其扩展到ELECTRE方法中，该方法能够克服以往决策问题中所遇到的复杂模糊不确定信息难处理的问题，具有简单实用的特点，使之能够被应用到更多的领域。

1 区间中智集及其可能度

1.1 区间中智集

定义一［8］：设X是一个对象集，x是对象集X中的元素，X的一个中智集A可以表示为

其中，TA（x），IA（x）和FA（x）是隶属于］0-，1+［的标准和非标准的子集，分别表示隶属度、犹豫度、非隶属度，所以，0-≤TA（x）+ IA（x）+ FA（x）≤3+。

定义二［9］：设X是一个对象集，x是对象集X中的元素，X的一个区间中智集A可以表示为

其中，TA（x），IA（x）和FA（x）分别表示隶属度、犹豫度、非隶属度，是隶属于［0，1］的子集，并且0≤sup［TA（x）］+ sup［IA（x）］+ sup［FA（x）］≤3。

我们可以用x =（［TL，TU］，［IL，IU］，［FL，FU］）去表示区间中智集中的元素，也就是区间中智数。

定义三［9］：设x =（［TL1，TU1］，［IL1，IU1］，［FL1，FU1］），y =（［TL2，TU2］，［IL2，IU2］，［FL2，FU2］）是两个区间中智数，则它们之间的Hamming距离可以定义为：

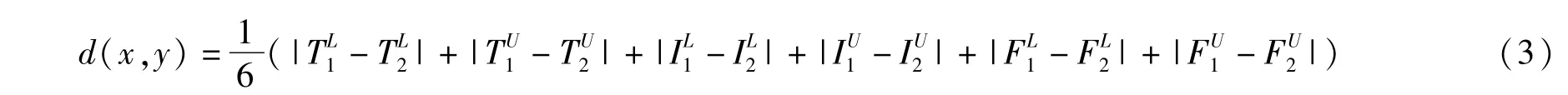
定理一［10］：设x =（［TL1，TU1］，［IL1，IU1］，［FL1，FU1］），y =（［TL2，TU2］，［IL2，IU2］，［FL2，FU2］和z =（［TL3，TU3］，［IL3，IU3］，［FL3，FU3］）是三个区间中智数，由定义三定义的距离公式满足以下4个性质：

（1）0≤d（x，y）≤1

（2）d（x，x）=0

（3）d（x，y）= d（y，x）

（4）假设x≺y≺z，则d（x，z）≥d（x，y）且d（x，z）≥d（y，z）

定义四［20］：设x =（［TL1，TU1］，［IL1，IU1］，［FL1，FU1］）和y =（［TL2，TU2］，［IL2，IU2］，［FL2，FU2］）是两个区间中智数，其运算规则如下：

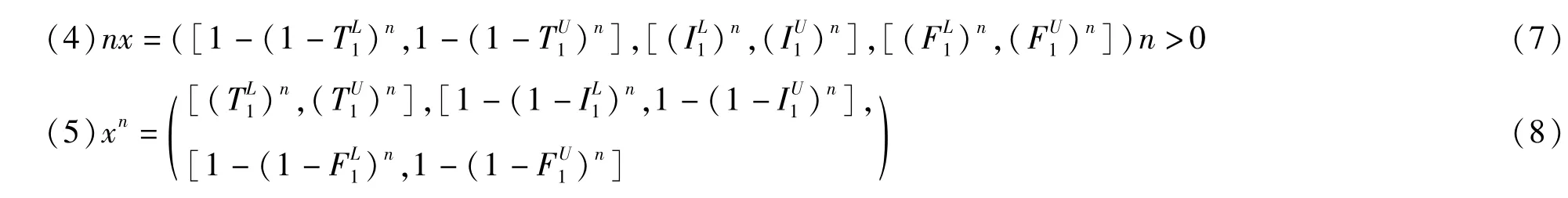
定理二［20］：设x =（［TL1，TU1］，［IL1，IU1］，［FL1，FU1］）和y =（［TL2，TU2］，［IL2，IU2］，［FL2，FU2］）是两个区间中智数，其运算规则满足如下的运算关系：

1.2 区间中智数的可能度

定义五［21］：假设x =［a，b］和y =［c，d］为两个区间数，那么两者之间的可能度公式为

区间数的可能度具有以下性质：

公理1：0≤P（x≥y）≤1

公理2：若a＞d，则P（x≥y）=1；若b＜c，则P（x≥y）=0

公理3：P（x≥y）+ P（x≤y）=1

公理4：若a = c，b = d，则P（x≥y）= P（x≤y）=0.5

公理5：若P（x≥y）≥0.5，P（y≥z）≥0.5，则P（x≥z）≥0.5。当且仅当P（x≥y）= P（y≥z）=0.5，则P（x ≥z）=0.5

公理6：若P（x≥y）=1，则P（x≥z）≥P（y≥z）

定义六［19］：假设G1=（［a1，b1］，［c1，d1］）和G2=（［a2，b2］，［c2，d2］）是两个区间直觉模糊数，那么两者之间的可能度公式为

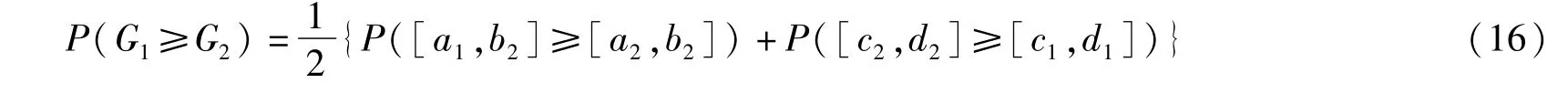
区间直觉模糊数的可能度具有以下性质：

公理7：0≤P（G1≥G2）≤1

公理8：P（G1≥G1）=0.5

公理9：P（G1≥G2）+ P（G2≥G1）=1

基于中智数的犹豫度与非隶属度的性质，本文在区间直觉模糊数的基础上定义了区间中智数的可能度。

定义七：假设N1=（［a1，b1］，［c1，d1］，［e1，f1］）和N2=（［a2，b2］，［c2，d2］，［e2，f2］）是两个区间中智数，那么两者之间的可能度公式为

很显然，区间中智数同样具有如下简单性质：

公理10：0≤P（N1≥N2）≤1

公理11：P（N1≥N1）=0.5

公理12：P（N1≥N2）+ P（N2≥N1）=1

2 基于区间中智集的改进ELECTRE方法

步骤一：对于在同一个指标Ck（k =1，2，…，n）下的m个方案进行两两比较，建立区间中智数的可能度矩阵：

Pkm×m矩阵是一个互补判断矩阵，它包含了m个方案相互比较的可能度信息，其元素是所有方案两两比较的可能度值。

步骤二：根据排序公式［22］，对互补判断矩阵Pkm×m进行分析，计算决策矩阵：

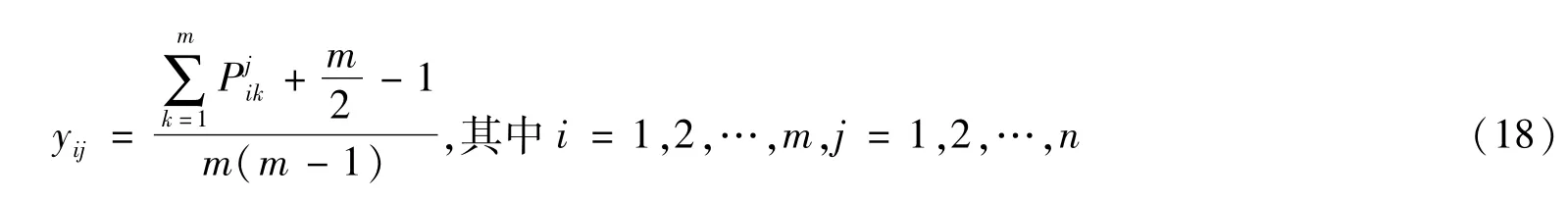
yij的次序关系能够反映m个方案的次序关系，所以用它替代原有的评估值不会影响m个方案的次序关系。经映射后形成的决策矩阵为：

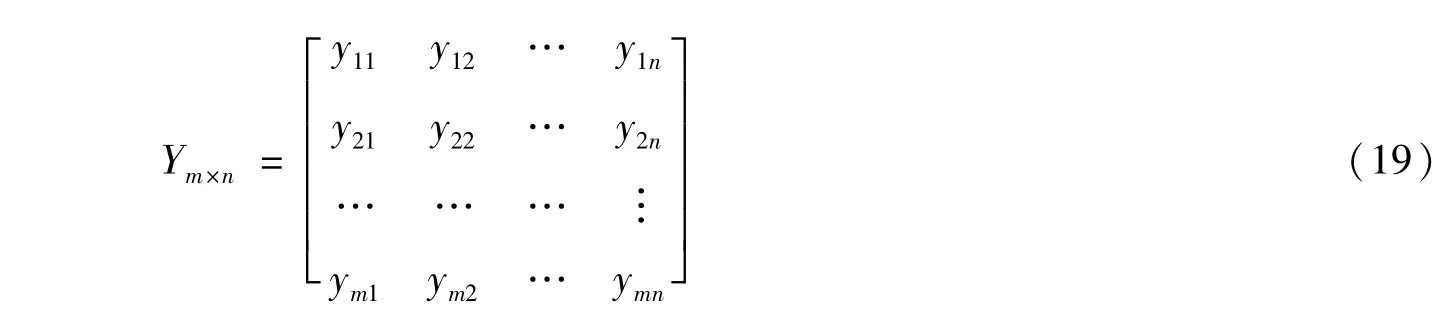
其中，元素yij表示第i个方案第j个指标经映射后的决策数值。

步骤三：把Y矩阵进行规范化得到规范化矩阵R：

步骤四：构造优先关系并计算优先度矩阵：

对于任意一个指标Cj，第k个和第i个方案之间的次序关系可由Rm×n矩阵中元素rkj和rij的大小来表示。若方案Ak等价于方案Ai，则rkj= rij；若方案Ak优于方案Ai，则rkj＞rij；若方案Ak劣于方案Ai，则rkj＜rij；若方案Ak优于或等价于方案Ai，则rkj≥rij；若方案Ak劣于或等价于方案Ai，则rkj≤rij。

J（k，i）=｛j｜1≤j≤n，∀Cj：rkj≥rij｝表示方案Ak优于或等价于方案Ai（rkj≥rij）的指标集合；J-（k，9）=｛j｜1≤j≤n∀Cj：rkj＜rij｝表示方案Ak劣于方案（rkj＜rij）的指标集合。

计算相对优先度矩阵CM：

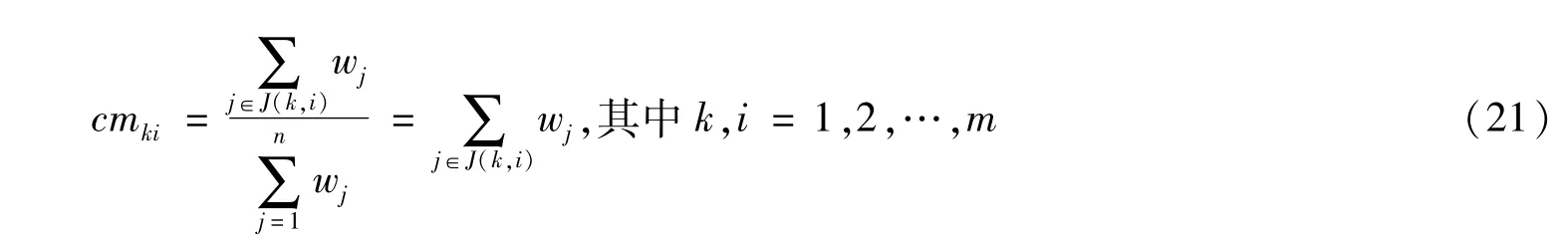
其中的元素cmki表示方案Ak优于方案Ai的程度。

步骤五：计算相对劣势矩阵DM：

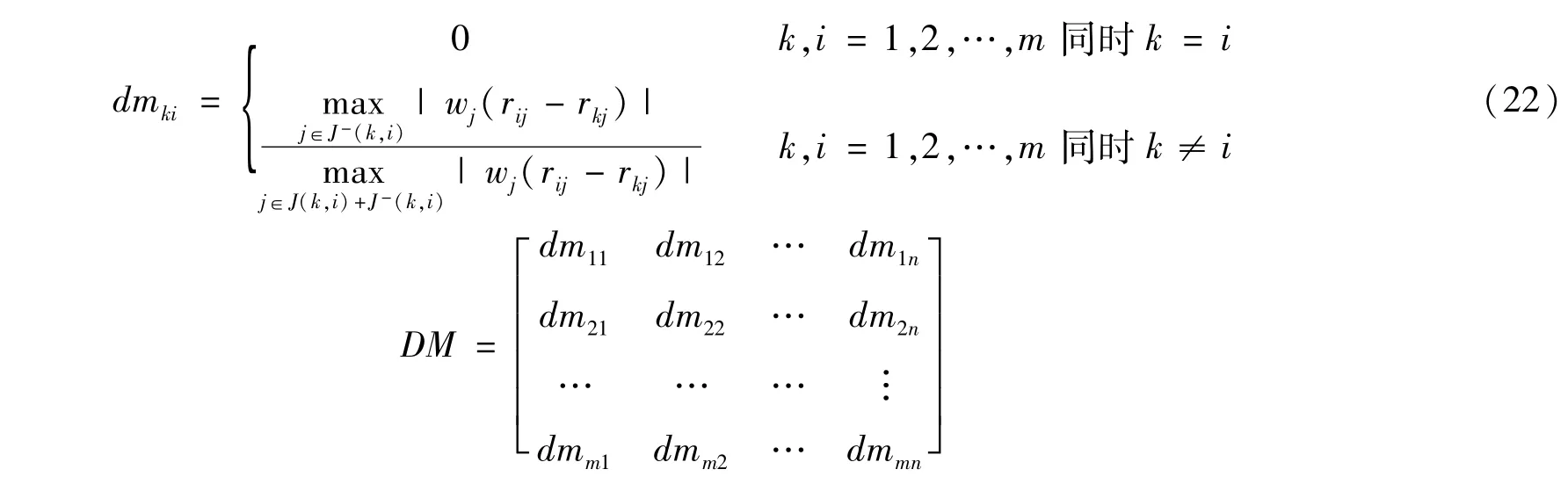
其中，元素dmki表示方案Ak比方案Ai的劣势指数。

比较发现，cmki只含有指标权重信息，而dmki不仅含有权重信息，还包含指标值信息，所以相对优先度和相对劣势度并没有互补性。dmkj反映了方案Ak较方案Ai的相对劣势程度，dmki的值越小越表示方案Ak劣于方案Ai的可能性就越小。

步骤六：计算修正综合加权矩阵E：

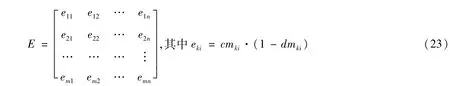
步骤七：计算净优势值δk：

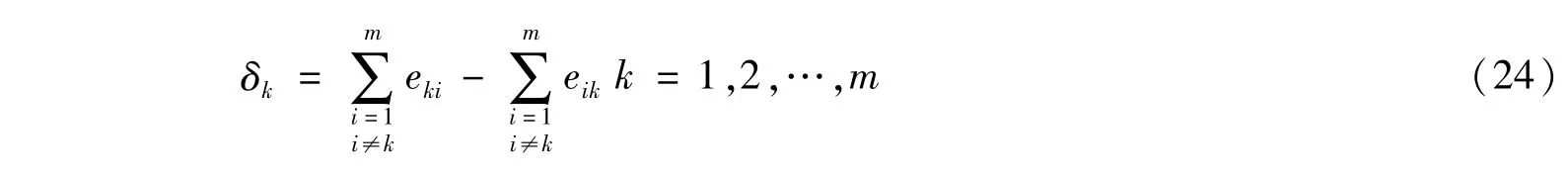
步骤八：排序：

δk的值越大方案Ak就越好，按照步骤七得到的δk的大小进行排序，就可以得到最终方案的优劣排序。

3 实例分析

为了验证这个方法的有效性，采用一个例子［23］进行计算、比较和分析。有一个投资公司想要选择一个最好的投资项目进行投资。有四个公司的项目可以选择：A1是一个汽车公司；A2是一个食品公司；A3是一个电脑公司；A4是一个军火公司。投资公司进行选择时要考虑3个指标：C1是风险控制水平；C2是潜在发展水平；C3是创新能力。3个指标的权重为w =（0.35，0.25，0.4）T，对各个方案的评价指标以区间中智数给出，其评价结果如矩阵R所示。

步骤一：利用公式（15）、（16）、（17）计算每一个指标Cj下的可能度矩阵：

步骤二：利用公式（18），得出最终的优势度矩阵Y：

步骤三：通过公式（20），得出规范化决策矩阵R：

步骤四：通过公式（21），计算相对优势度矩阵CM：

步骤五：通过公式（22），计算相对劣势矩阵DM：

步骤六：通过公式（23），计算修正综合加权矩阵E：

步骤七：通过公式（24），计算净优势值：

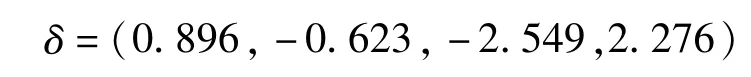
步骤八：排序结果为A4＞A1＞A2＞A3。

所以，四个投资方案中，军火公司的项目为最好的投资项目。

4 结束语

区间中智数能很好地处理决策信息的不确定性、不完全性和不一致性，本文针对评价值为区间中智数的多属性决策问题，介绍了一种改进了的ELECTRE方法，不仅可以解决决策值为不明确的数据的方案之间的排序问题，同时还能够弥补参数过多、排序过程复杂所遇到的问题。由于区间中智数在描述评价结果方面的优势和ELECTRE方法应用性强的优点，本文为决策信息模糊性较大并且需要考虑级别优先关系的决策问题提供了一个切实可行的方法。在以后的研究中，还要进一步扩大这种新方法的应用范围，不断地完善这种方法也是必不可少的。

参考文献：

［1］赵勇，徐轲，张光准.基于不确定性多目标决策的政府采购评标方法研究［J］.山东财经大学学报，2015，27（3）：61 -67.

［2］姚兴华，李秀荣，高爱霞.山东省中小物流企业竞争力评价研究——基于层次分析法与模糊综合评判［J］.山东财经大学学报，2015，27（2）：96 -104.

［3］朱磊，于伟洋.董事会治理，CEO过度自信与我国企业并购决策［J］.山东财经大学学报，2015，27（1）：107 -115.

［4］ZADEH L A.Fuzzy Sets［J］.Information and Control，1965，8（3）：338 -353.

［5］ATANASSOV K T.Intuitionistic Fuzzy Sets［J］.Fuzzy Sets and Systems，1986，20（1）：87 -96.

［6］ATANASSOV K T，GARGOV G.Interval Valued Intuitionistic Fuzzy Sets［J］.Fuzzy Sets and Systems，1989，31（3）：343 -349.

［7］ATANASSOV K T.Operators over Interval Valued Intuitionistic Fuzzy Sets［J］.Fuzzy Sets and Systems，1994，64（2）：159 -174.

［8］SMARANDACHE F A.Unifying Field in Logics：Neutrosophic Logic［J］.Philosophy，1999，87（4）：120 -141.

［9］WANG H，SMARANDACHE F，ZHANG Y，et al.Single Valued Neutrosophic Sets［J］.Review of the Air Force Academy，2010，1（16）：10 -14.

［10］WANG H，SMARANDACHE F，SUNDERRAMAN R，et al.Interval Neutrosophic Sets and Logic：Theory and Applications in Computing：Theory and Applications in Computing［M］.Infinite Study，2005.

［11］LIU W，LIU P.Hybrid Multiple Attribute Decision Making Method Based on Relative Approach Degree of Grey Relation Projection ［J］.African Journal of Business Management，2010，4（17）：3716 -3724.

［12］WEI G W，YU W.Model of Grey Relational Analysis for Interval Multiple Attribute Decision Making with Preference Information on Alternatives［J］.Chinese Journal of Management Science，2008（1）：23.

［13］LIU P.Multi - attribute Decision - making Method Research Based on Interval Vague Set and TOPSIS Method［J］.Technological and Economic Development of Economy，2009（3）：453 -463.

［14］YUE Z.An Extended TOPSIS for Determining Weights of Decision Makers with Interval Numbers［J］.Knowledge - Based Systems，2011，24（1）：146 -153.

［15］OPRICOVIC S，TZENG G H.Compromise Solution by MCDM Methods：A Comparative Analysis of VIKOR and TOPSIS［J］.European Journal of Operational Research，2004，156（2）：445 -455.

［16］LIU P，ZHANG X.Research on the Supplier Selection of a Supply Chain Based on Entropy Weight and Improved ELECTRE - III method［J］.International Journal of Production Research，2011，49（3）：637 -646.

［17］刘培德，关忠良.一种基于语言变量的多属性决策ELECTRE方法［J］.数学的实践与认识，2011，41（16）：65 -71.

［18］吴彩虹，陈常青.区间数多属性决策的一种ELECTRE方法［J］.长沙大学学报，2006，19（5）：14 -17.

［19］WAN S，DONG J.A Possibility Degree Method for Interval - valued Intuitionistic Fuzzy Multi - attribute Group Decision Making ［J］.Journal of Computer and System Sciences，2014，80（1）：237 -256.

［20］YE J.Similarity Measures Between Interval Neutrosophic Sets and Their Applications in Multicriteria Decision - making［J］.Journal of Intelligent and fuzzy Systems，2014，26（1）：165 -172.

［21］徐泽水，达庆利.区间数排序的可能度法及其应用［J］.系统工程学报，2003，18（1）：67 -70.

［22］徐泽水.模糊互补判断矩阵排序的一种算法［J］.系统工程学报，2001，16（4）：311 -314.

（责任编辑 王玉燕）

［23］YE J.Similarity Measures Between Interval Neutrosophic Sets and their Applications in Multicriteria Decision - making［J］.Journal of Intelligent and fuzzy Systems，2014，26（1）：165 -172.

ELECTRE Method and Its Application in Multiple Attribute Decision Making Based on INS

LIU Peide1，2，LI Honggang1，WANG Peng1，LIU Junlin1
（1.School of Management Science and Engineering，Shandong University of Finance and Economics，Jinan 250014，China；2.School of Economics and Management，Civil Aviation University of China，Tianjin 300300，China）

Abstract：Aimed at solving information uncertainty，incompleteness and inconsistency in multiple attribute decision making，an ELECTRE method based on interval neutrosophic numbers is proposed with the possibility degrees of different data types taken into consideration.This paper firstly introduces interval neutrosophic set（INS）and possibility degree，and then in view of the deficiency of traditional ELECTRE method which adopts the real number to represent evaluation information，proposes an extended ELECTRE method by combining ELECTRE method and interval neutrosophic numbers.Based on scheme attribute values shown by interval neutrosophic numbers，the priority and disadvantage of each scheme group are calculated compared with all the other schemes before the schemes are ranked according to their net advantage degree.The feasibility and effectiveness of this proposed method are verified with an example.

Keywords：interval neutrosophic number；ELECTRE method；multiple attribute decision making

作者简介：刘培德，男，山东潍坊人，博士，山东财经大学管理科学与工程学院教授，博士生导师，中国民航大学经济与管理学院教授，研究方向：决策理论与方法、信息管理与决策支持，Email：liupd966@126.com；李洪刚，男，山东德州人，山东财经大学管理科学与工程学院硕士研究生，研究方向：模糊多属性决策；王鹏，男，山东临沂人，山东财经大学管理科学与工程学院硕士研究生，研究方向：模糊多属性决策；刘俊麟，女，山东淄博人，山东财经大学管理科学与工程学院硕士研究生，研究方向：模糊多属性决策。

基金项目：国家自然科学基金面上项目“基于中智集的模糊多属性决策理论、方法与应用研究”（7147117）；国家自然科学基金面上项目“基于二维不确定语言信息的模糊多属性群决策理论、方法及应用研究”（71271124）；国家软科学计划项目“基于模糊与优化理论的黄河三角洲高效生态经济区生态系统健康评价与生态政策研究”（2014GXQ4D192）；泰山学者工程专项经费资助。

中图分类号：C934

文献标识码：A

文章编号：2095 -929X（2016）02 -0080 -08

修回日期：2015 -11 -09