GIS优化SRM储流函数模型变量与参数方法研究

俞　荭，程　钢，李任之

(1.河南理工大学 矿山空间信息技术国家测绘地理信息局重点实验室，河南 焦作 454000; 2.河南理工大学 测绘与国土信息工程学院，河南 焦作 454000)



GIS优化SRM储流函数模型变量与参数方法研究

俞荭1,2，程钢1,2，李任之1,2

(1.河南理工大学 矿山空间信息技术国家测绘地理信息局重点实验室，河南 焦作 454000; 2.河南理工大学 测绘与国土信息工程学院，河南 焦作 454000)

摘要：水文模型的结构确定后，模型参数的选择对水文模型整体性能和水文预报结果的好坏有着至关重要的影响。为使得模型的输出值能够尽可能地接近实际值,文中结合数字高程模型(DEM)和流域地质资料，使用GIS方法分别从优化数据源和加入地质因素影响分析优化模型参数两方面入手，对SRM储流函数模型进行优化，并以北海道沙流川流域为例对上述方法进行检验，结果说明了方法的可行性。

关键词：水文模型；GIS；SRM模型；地质因素

概念性水文模型是3种主要水文模型之一，它是以水文现象的物理概念和一些经验公式为基础构造的，能有效反映流域的水文物理过程[1]。典型的水箱汇流模型、等流时线模型、滞后演算法等，都是用不同的概念性元素模拟洪水波的运移过程[2-3]。洪水波的运移现象与流域特性和河网结构等信息密切相关，而传统的概念性模型却只考虑了气候因素的影响，忽略了地貌因素的作用[4]。于是，随着地形信息技术的发展，便出现了很多将地形信息用于概念性模型、以及寻求概念性模型与地形信息之间相关关系的研究[5-6]。中津川诚教授，奥全宗一郎等人在Dr. Kiyoshi Hoshi等前人的基础上尝试将SRM概念性模型与下垫面地质环境相结合，实现了利用模型参数来综合反映下垫面地质、地貌等因素对径流形成各环节的影响[7]。谢平等则将 Horton 的地貌律理论应用到概念性汇流模型中，建立了不同的概念性流域地貌汇流模型[8]。这些研究利用地形、地质等数据对概念性模型进一步延伸和发展。

本文拟结合数字高程模型(DEM)和流域地质资料，运用GIS技术分别从提高数据源准确度和加入地质因素优化模型参数两方面入手，对SRM储流函数模型展开研究，并以北海道沙流川流域为例，探讨地形、地质因素对于该模型的优化能力以及存在的不足。

1SRM模型原理

SRM(Storage Routing Model)储流函数模型是一种流域流量解算模型，是水箱模型的一种具体应用，属于概念型水文模型的一种。该模型使用两种类型的函数解算方法：①一段综合型储流函数法，其示意图如图1(a)所示；②二段双级联存型储流函数法，示意图如图1(b)所示。一段综合型储流函数法和二段双级联存型储流函数法的数学模型如表1所示，此类模型可以根据流域降雨量的大小，计算监测流域流量变化，预测洪水流量，其参数可以通过降雨量和实际的流量数据进行改善和优化。

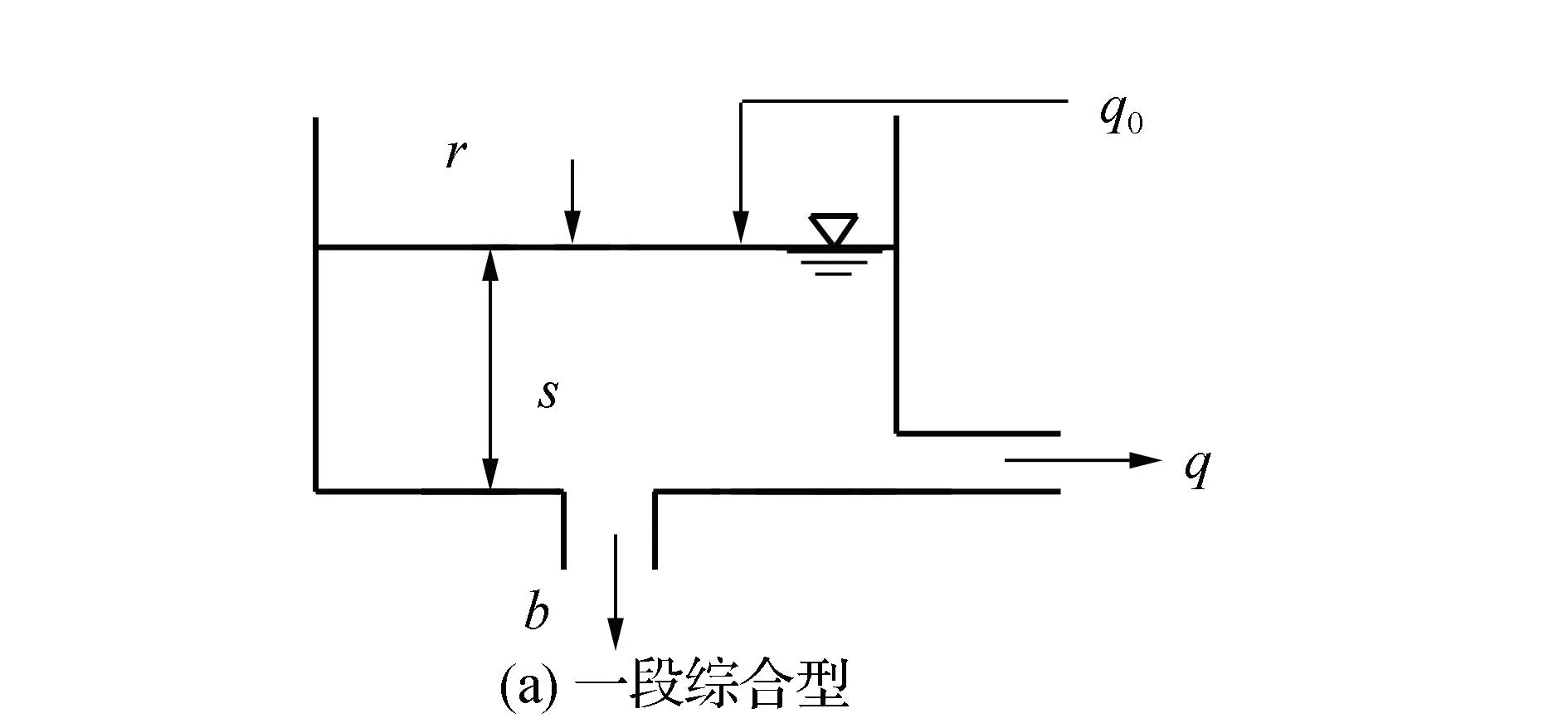
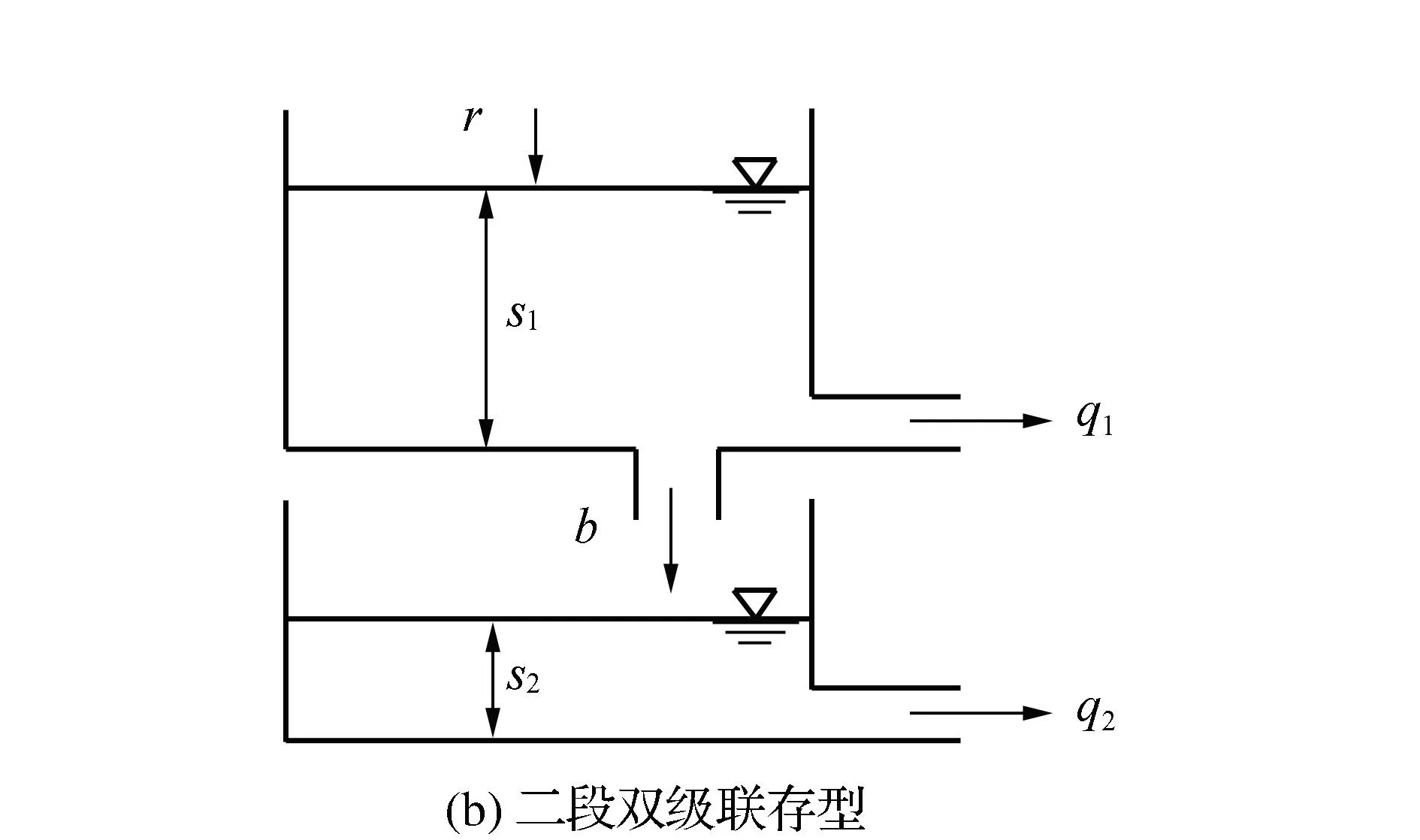
图1　储流函数法模型示意图

本文主要对一段法中的参数c11，c12，c13和二段法中的参数c21，c22，c23，Tc值进行优化。

2GIS方法优化模型参数实验

选取日本北海道沙流川Nibutani大坝上游区域作为实验研究区域，选择2002-08-08—2002-08-11发生在该区域的小洪水为研究事件。采用10 mDEM基础地形信息数据和日本国土交通省数值资料(G05-54M)作为基本地质数据。

表1　储流函数法数学模型

2.1优化降雨量数据

降雨数据是SRM模型的输入数据源，它的精确与否直接影响着模型预测的精度[9]。所以，本文从优化降雨数据入手，首先对数据源进行优化。

主要的降雨量求取方法有算术平均法和加权平均法[10]。前者适用于地形起伏不大，降水分布均匀，测站布设合理的情况下，如式(1)，其中pi表示各观测点的降雨量(下同)；后者选择有代表性的地点作为降水观测点，把每个测点控制的面积ai和总面积A的比值作为各测点降水量的权重，按式(2)计算流域平均降水量。

(1)

(2)

前一种方法不足之处在于，无法准确反应流域地形变化，后一种方法比前一种方法更加准确，其关键在于如何确定每个观测区域的控制范围以及这些控制范围能否覆盖到流域的全部面积。为解决以上问题，利用Arcgis软件，对DEM数据进行流向、汇流、河网分析等一些列处理，采用Thiessen多边形知识，根据流域边界以及各观测站坐标进行Thiessen多边形区域划分以Thiessen多边形的面积作为每个观测点所代表的区域面积，进而采用式(3)计算全流域的平均降雨量，得到研究区域的观测点范围划分情况，如图2所示。

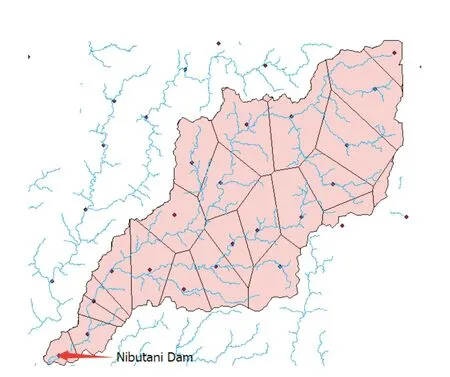
图2　流域Thiessen多边形法分割

(3)

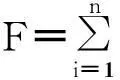
Thiessen多边形划分方法本质上是加权平均法的延伸，此方法的优点在于，可以更加合理地划分各观测站影响区域，更加全面地覆盖整个流域面积。将流域作为一个整体进行计算，从而得到更加准确的平均降雨量数据。

2.2利用地质数据优化模型参数

本文将地质数据导入Arcgis中，运用Arcgis空间分析功能，根据所在像元的属性数值进行地质区分，得到的研究区域地质分类图如图3(图中不同颜色的网格代表不同的地质成分)所示。沙流川流域以及北海道众河川的地质成分见表2。

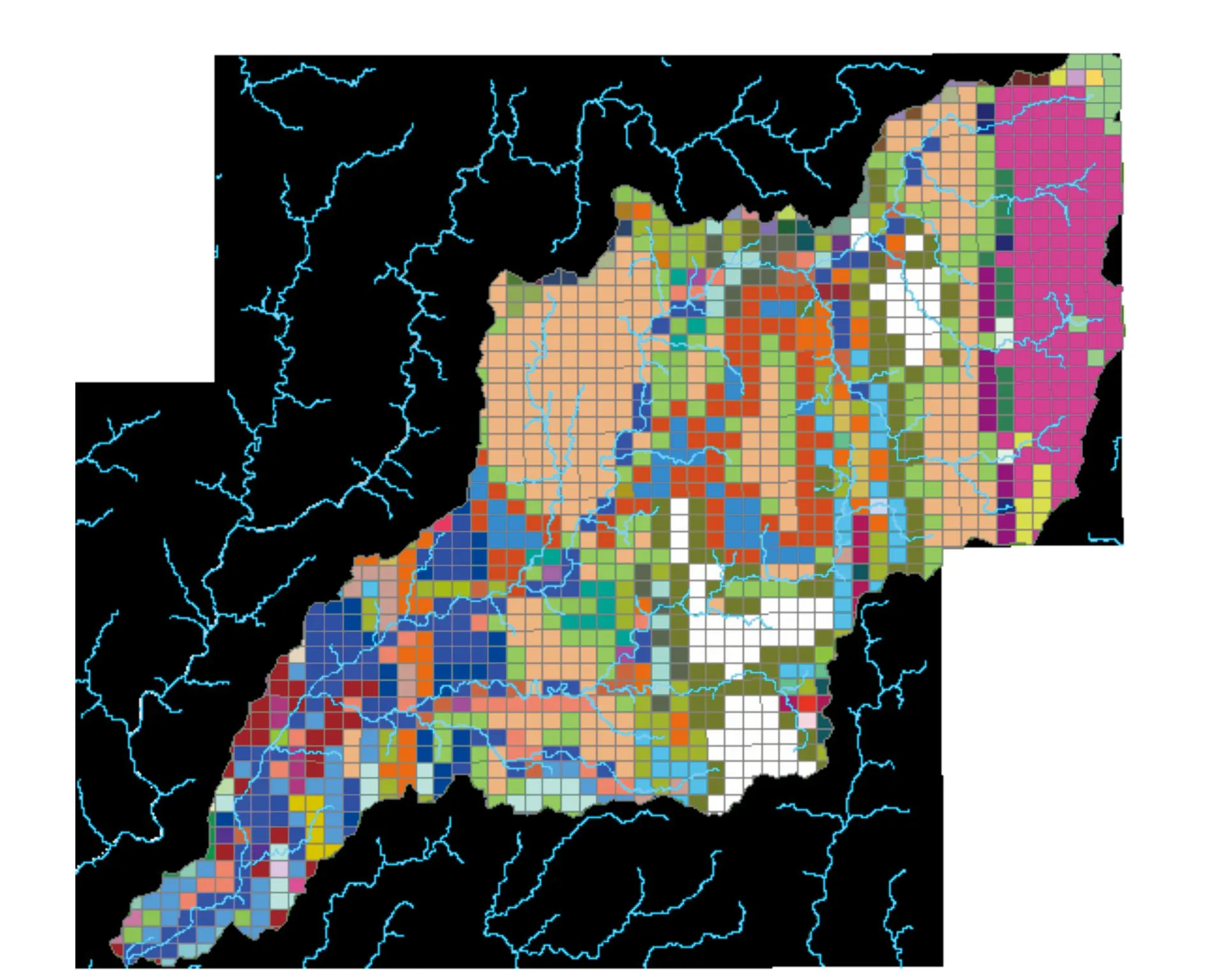
图3　研究区域地质分类图

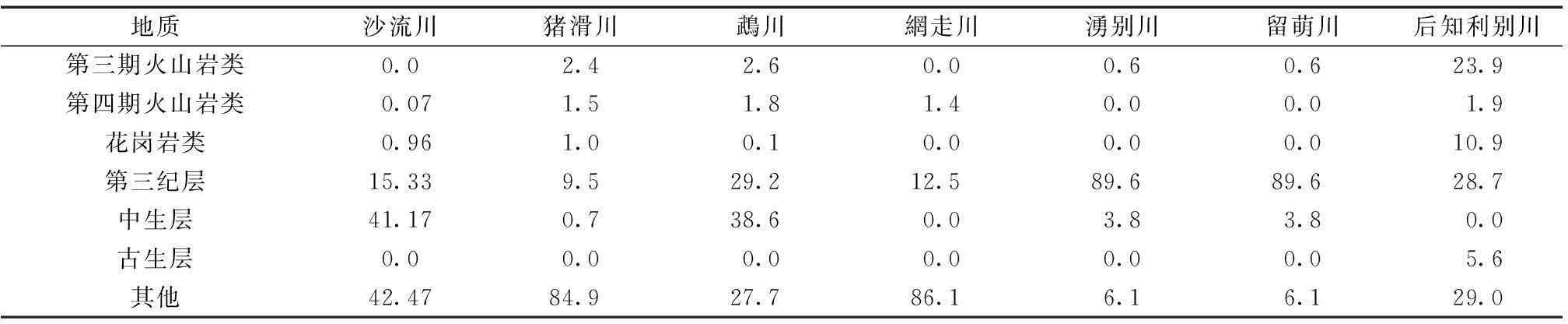
表2　北海道各河川地质面积率　%

根据上田申也提出的回归方程分析方法，采用北海道各流域的地质面积率资料，建立模型参数与地质面积率的函数方程式(4)～(10)，旨在探寻地质面积率变化对模型参数的影响大小。

c11=9.874+2.432g1+5.231g2+7.309g3-

(4)

c12=0.091-0.004g1+0.071g2-0.018g3-

(5)

c13=1.555-0.823g1+0.404g2+0.716g3+

(6)

c21=7.968+0.959g1+1.812g2+4.197g3-

(7)

c22=0.141+0.017g1+0.446g2+0.314g3-

(8)

c23=1.976-0.921g1+0.966g2+2.613g3+

(9)

Tc=80.212-29.404g1-2.276g2-47.004g3-9.334g4-44.983g5+34.591g6.

(10)

其中:c11,c12,c13和c21,c22,c23，Tc值为一段储留函数法和二段储留函数法中的参数，g1，g2，g3，g4，g5，g6，分别代表第三季火山岩类、第四纪火山岩类、花岗岩、第三纪层、中生层、古生层的面积率。

3实验结果分析

通过实验得到优化后的数据源和参数后，借助IRIC软件进行SRM模型的运算，分别得到一段法和二段法计算的洪水流量数据，绘制成流量曲线图(见图4)。通过图4可知，与使用经验参数计算所得曲线相比，使用优化后的降雨量和加入地质数据优化得到的参数解算所得数据能够更好地反映洪水流量的变化趋势，且对于洪峰到来时间的预测更加准确。但无论是一段储流函数法还是二段函数法，对于模型优化后曲线峰值和洪峰到达时间预测还有些许差异。

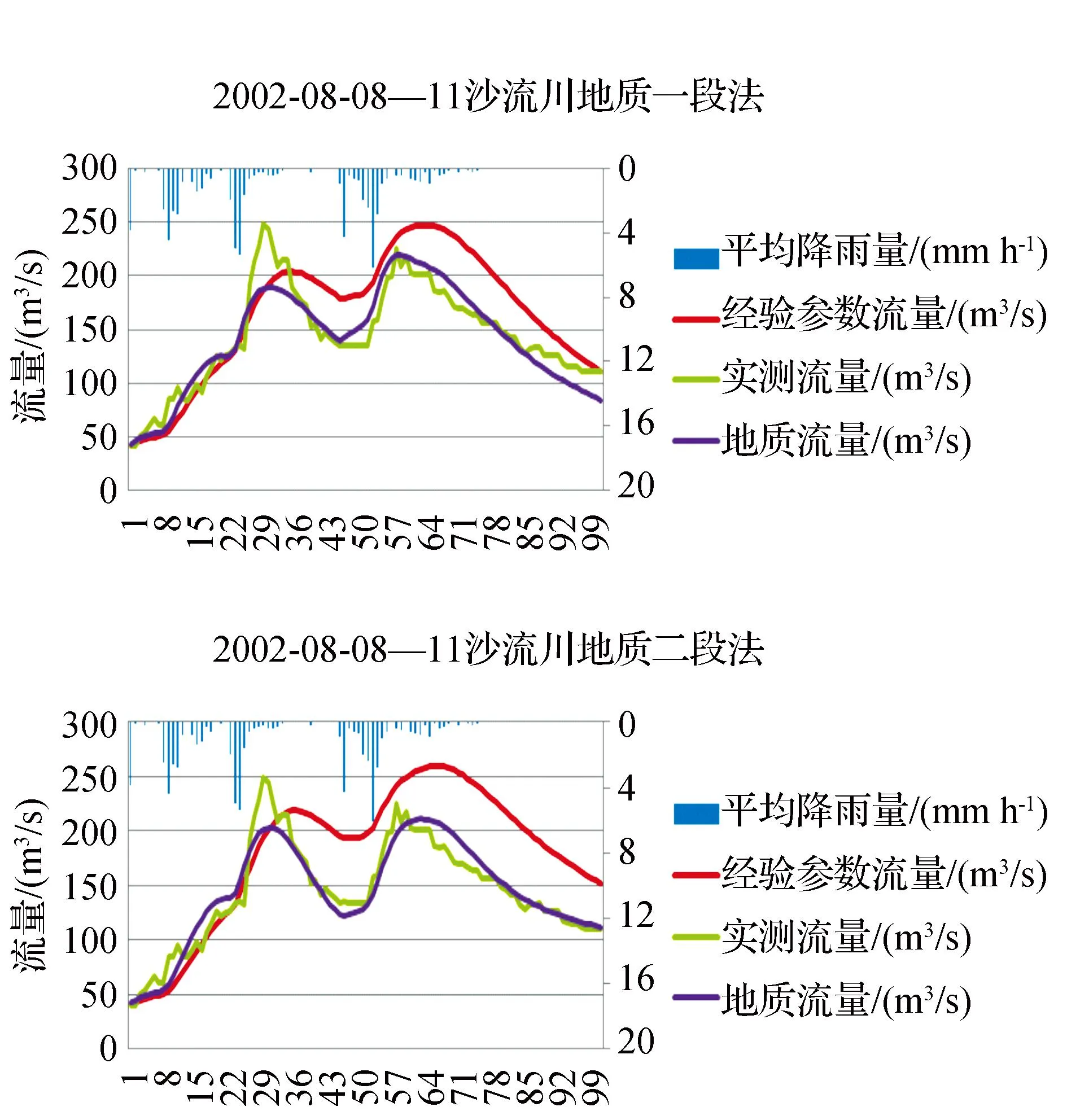
图4　沙流川洪水流量计算结果比较

为了更准确地比较优化后的结果同实际观测结果之间的偏差，本文选用Nash-Sutcliffe系数式(11)和均方根误差(RESM)，定量评价实测流量与计算流量的误差。

(11)

式中：N为计算时间数,q0(i)为i时的实测流量,qc(i)为i时的计算流量，qav为实测流量的平均值。计算结果如表3所示。

表3　参数优化前后预测结果对比

从表3的比较结果看，模型输入量和参数优化后，NASH系数有所提高，说明模型比优化前更加贴近真实值，而RESM值的减少也同样说明了模型优化后的预测精度有所提高。这一点在NASH系数上也有很好的表现。

4结束语

运用GIS优化洪水预测模型的方法已经成为一种提高模型准确度的十分有效的手段。与传统方法相比，本文运用GIS知识，通过优化模型降雨数据源，加入地质因素影响等方法，实现了优化SRM储留函数模型参数的目的。所提出的优化数据源和加入地质因素优化SRM储留函数模型参数的方法，可以更好地反映流域地质空间分布的不均一性，使得模拟的结果更加接近实际情况。参数优化后，可以更加准确地预测洪水流量大小、反映洪峰变化趋势。但该方法也存在一些不足，使用GIS优化SRM模型的方法尚不能对于洪水峰值以及洪峰到达时间做出准确预测。今后将尝试根据流域的实际情况将汛期化分为前汛期、主汛期、后汛期几个阶段,在各个阶段确定不同的模型参数推算出流过程，以提高预测的准确度。

参考文献：

[1]王中根,刘昌明,吴险峰.基于DEM的分布式水文模型研究综述[J].自然资源学报,2003,18(2):168-173.

[2]郭俊,周建中.新安江模型参数多目标优化研究[J].水文,2013,33(1):3-7.

[3]杨传国,余钟波.大尺度分布式水文模型数字流域提取方法研究[J].地理科学进展,2007,26(1):68-74.

[4]周小军,王光霞,薛志伟,等.基于DEM化简的等高线综合研究[J]. 测绘工程,2014,23(2):10-14.

[5]胡效宁，路全福.半干旱地区水库洪水预报中对水箱模型改进的研究和应用[J].海河水利,1999(1):3-6.

[6]夏岑岭,刘之俭,张效武,等.缺乏水文资料流域汇流模型的地貌学识别[J].合肥工业大学学报(自然科学版),1995，18(S1)：94-97．

[7]ZHANG S Y, CORDERY I, SHARMA A. A volume law for specification of linear channel storage for estimation of large floods. Water Resource. Res. 2000，36(6)：1535-1543.

[8]谢平,孙志.分散型流域地貌汇流模型的总体构想[J]．水电能源科学，2001，19(2)：28-31.

[9]DUAN Q, GUPTA V K, SOROOSHIAN S. Effective and efficient global optimization for conceptual run-off models[J].Water Resources Research,1992,28(4):1015-1031.

[10] GIANNONI F,ROTH G,RUDARI R.A Semi-Distributed Rainfall-Runoff Model Based on a Geomorphologic Approach[J]. Phys. Chem. Earth (B), 2000,25(7-8): 665-671.

[责任编辑：刘文霞]

A study of optimization of input data and parameters for SRM hydrological model using GISYU Hong1,2，CHENG Gang1,2，LI Renzhi1,2

(1.Key Laboratory of Mine Spatial Information Technologies, National Administration of Surveying, Mapping and Geoinformation, Henan Polytechnic University, Jiaozuo 454000, China; 2.School of Surveying and Land Information Engineering, Henan Polytechnic University, Jiaozuo 454000， China)

Abstract：Due to the fact that the hydrological model structure is determined, the selection of model parameters has a vital influence on the overall performance of hydrological model and the forecast results. To make sure the output value of the model can be as much as possible close to the actual value, this paper, based on the digital elevation model (DEM) and the geological data, uses GIS method to make the improvement of rainfall data sources and focus the geological factors for analysis. Taking Saru river in Hokkaido,Japan as the experimental field,it proves the possibility to realize the parameter optimization of SRM model.

Key words：hydrological model; GIS; geological factors; SRM model

中图分类号：P208

文献标识码：A

文章编号：1006-7949(2016)06-0024-04

通讯作者：程钢(1981-)，男，副教授，博士，硕士生导师.

作者简介：俞荭(1989-)，女，硕士研究生.

基金项目：国家自然科学基金资助项目(41001226);河南省高等学校骨干教师资助计划(2012GGJS-055); 河南省高校科技创新团队支持计划(14IRTSTHN026);矿山空间信息技术国家测绘地理信息局重点实验室开放基金(KLM201408);河南省教育厅人文社会科学研究项目(2014-qn-068); 河南理工大学博士基金(B2010-9)

收稿日期：2014-12-27