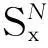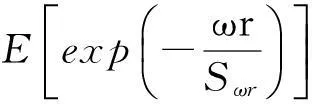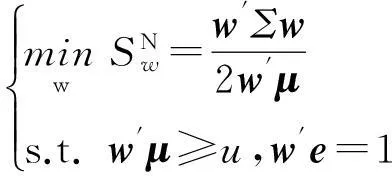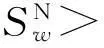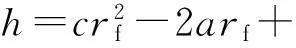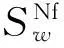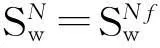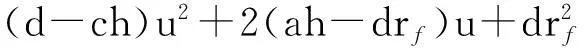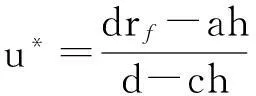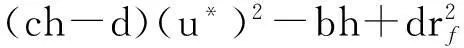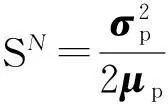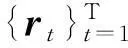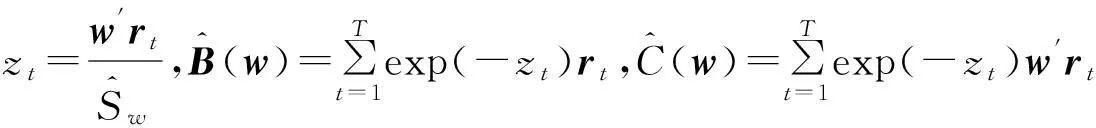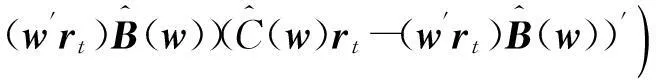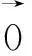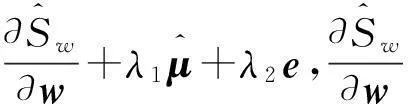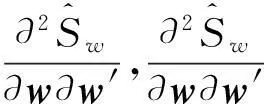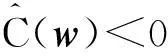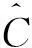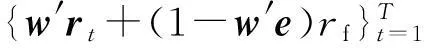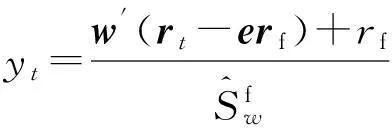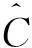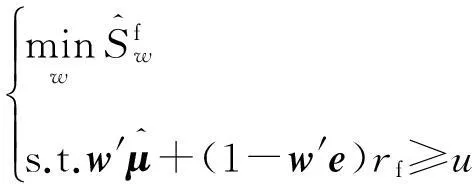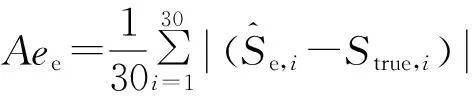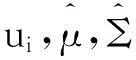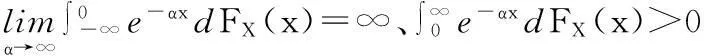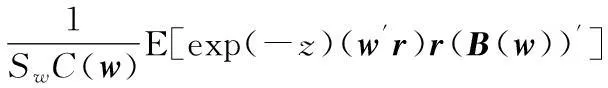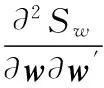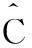基于均值-AS模型的资产配置①

曾　燕， 黄金波

(1. 中山大学岭南(大学)学院， 广州 510275； 2. 广东财经大学金融学院， 广州 510320)



基于均值-AS模型的资产配置①

曾燕1， 黄金波2

(1. 中山大学岭南(大学)学院， 广州 510275； 2. 广东财经大学金融学院， 广州 510320)

摘要：AS指标是诺贝尔经济学奖得主Aumann与其合作者Serrano近期基于不确定条件下的选择理论提出的新的风险度量指标，具有诸多优点，被学者们广泛关注.本文基于均值-AS模型研究了正态分布和一般分布下的资产配置问题.在正态分布下，得到了组合边界的解析式，深入探讨了组合边界的特征.在一般分布下，将AS指标的矩估计式嵌入均值-AS模型，实现了风险估计与投资组合优化同步进行.在较弱的条件下，证明了均值-AS模型是凸优化问题，可基于迭代思想设计算法得到模型的数值解.蒙特卡洛模拟结果表明该模型和算法准确有效.最后，基于中国A股市场数据给出了实例分析.

关键词：均值-AS模型； AS指标； 组合边界； 矩估计

0引言

日常生活中人们常常需要在不确定环境下进行决策，从而形成了不确定条件下的选择理论.Diamond和Stiglitz[1]指出：人们在决定是否参与一项具有不确定性的游戏时，会考虑两个关键因素：一是该游戏的风险有多大，二是个人的风险偏好或风险承受能力如何.Arrow[2-3]和Pratt[4]定义了风险规避的概念，解决了第二个因素的度量问题.这是个主观的概念，依赖于个人的效用函数，然而他们未能解决第一个问题.该问题在金融风险管理领域得到了广泛研究，Marktowitz[5]的开拓性工作之一就是采用方差来度量风险.随后学者们提出了一些新的风险度量指标，如下半方差、下偏矩、在险价值(VaR)、条件在险价值(CVaR)等，并对收益-风险框架下的资产配置问题进行了深入研究.但是，金融风险领域的这些风险度量指标有以下两方面不足.第一，这些均为技术性指标，都是运用概率统计方法定义出来的，没有考虑人的经济行为.这些风险度量指标与人的风险偏好之间不能形成对偶关系.换句话说，倘若一方面利用这些指标得出资产的风险值，同时另一方面也可以通过一些方法得到人们的风险规避系数，但它们之间的关系无法确定.第二，这些风险度量指标大多数不满足随机占优单调性*随机占优单调性是指：如果一种资产收益率的分布一阶(或二阶)随机占优另一种资产的收益率分布，那么前一种资产的风险要小于后一种资产.[6].在不确定条件下的选择理论中，随机占优单调性是被广泛接受的能够客观刻画风险的理论[7-9].

为了弥补上述风险度量指标的不足，诺贝尔经济学奖得主Aumann与其合作者Serrano基于不确定条件下的选择理论，提出了新的风险度量指标，简称AS指标[6].该指标满足两个基本公理：对偶性和正齐次性，并具有一阶与二阶随机占优单调性.此外，他们还证明了任何满足对偶性和正齐次性的风险度量指标都是AS指标的正数倍.Homm和Pigorsch[10]在更为一般的假设下，证明了AS指标的存在性.Schulze[11]拓展了AS指标的应用范围，严格证明了相应条件下AS指标的存在性，并推导出收益率服从指数分布、泊松分布、Gamma分布、方差-Gamma分布等几种特殊分布下AS指标的解析式.为了解决AS指标只测度绝对风险的不足，Schreiber[12]建立了测度相对风险的风险度量指标的理论框架.Foster和Hart[13]在AS指标的启发下，提出了可替代AS指标且可操作的仅关心财富水平的风险指标.而Bali等[14]提出了更为一般的风险指标，拓展了Aumann和Serrano[6]及Foster和Hart[13]的研究，并推导出多种S&P500指数期权隐含的风险度量指标.在AS指标的应用方面，Homm 和Pigorsch[15]利用AS指标定义了投资表现指标，该指标拓展了夏普比率，包含了峰度、偏度等高阶矩的信息.如果投资者对这些信息比较关注，AS指标是更好的风险度量指标.此外，Chen等[16]基于AS指标得到了现货与期货的套期保值策略，给出了正态分布下最优套保比率的解析式，以及一般分布下最优套保比率的估计式.他们发现基于AS指标的套保比率统计上显著不同于基于方差的套保比率，基于AS指标的套保比率相对较低，并且该指标有更好的经济解释和理论性质，实证研究也支持上述理论发现.

对AS指标的相关研究还在持续深入，据笔者了解目前还没有学者探讨AS指标下的资产配置问题.本文尝试基于均值-AS模型对正态分布和一般分布下的资产配置问题进行探讨.在正态分布假设下，得到了不含无风险资产和含无风险资产时组合边界的解析式，并与均值-方差模型对比，深入探讨了组合边界的特征.在一般分布假设下，将AS指标的矩估计式嵌入投资组合决策模型，实现了风险估计与投资组合优化同步进行.在非常弱的条件下，证明均值-AS模型是凸优化问题，并可用数值算法得到其数值解.蒙特卡洛模拟结果表明基于AS矩估计量的模型和算法是有效且准确的.最后给出了一个基于我国股票市场数据的实证算例.

1AS指标的定义和性质

Aumann和Serrano[6]在具有不确定性赌局(gamble)决策的框架下提出了AS指标.假设随机变量x为某次赌局的净收益，ω为决策者的初始财富，假定决策者的效用函数为常绝对风险规避(CARA)效用函数

U(ω)=-γ-1exp(-γω)风险规避系数γ>0，决策者参与该项赌局将得到期望效用E[U(ω+x)].如果存在γ*使得

成立，则通过定义Sx∶=1/γ*>0，上式可写为

(1)

Aumann和Serrano[6]建议使用Sx作为该赌局的风险指标.他们直接由式(1)定义该风险指标，不需依赖效用函数的具体形式.只是在CARA效用函数下，该指标的定义式(1)正好可以由参与赌局的期望效用与不参与赌局的效用相等得到.基于此，Chen等[16]把CARA效用函数作为推导式(1)的纽带.从式(1)来看，该指标是个客观的数值，仅依赖于净收益的分布，不依赖于个人的任何特征，特别是不依赖个人的效用函数.

定理1随机变量x满足条件P(x<0)>0且E[x]>0时，方程(1)存在唯一正数解，其中P(·)表示概率，E[·]为期望算子.

P(x<0)>0表明该赌局存在损失的可能性.E[x]>0表明本文考虑的是风险规避者的决策问题，因为E[x]≤0时，风险规避者一定不会参与该赌局，此时风险可以定义为无穷大.现实中大部分投资者都是风险规避者，这样风险-收益权衡研究才有意义.可见条件P(x<0)>0和E[x]>0与现实很相符.若无特殊说明，下文假设这两个条件成立.

从AS指标的定义式(1)可看出，该指标相对于传统的金融风险度量指标有不少优点.例如，方差指标只关心离散程度而并不关心方向如何，它把向上和向下偏离都看作风险，而AS指标通过给予收益方更少的权重而给损失方更大的权重，弥补了方差这一缺点.夏普比率也经常被用作风险指标[15]，它隐含了个假设，即资产收益率的均值和标准差完全刻画了资产的收益与风险，然而金融市场上的实际数据常常表现出尖峰厚尾、非对称等特征，AS指标是资产收益率的矩生成函数，除均值和方差外，还考虑了高阶矩包含的信息.虽然VaR和CVaR是近年来被金融领域广泛采用的两大风险度量指标，已被写入了巴塞尔协议III及各国金融监管当局的官方文件，但是作为风险度量，这两个指标都有共同不足：只关心资产的损失方，而不考虑其收益方，即使在损失方，VaR也只关心某一设定概率下的最大损失门槛值，CVaR只关心超过这个门槛值的损失的期望.AS指标不仅考虑了损失还考虑了收益.此外，Aumann和Serrano[6]给出了AS指标的几个重要性质并对它们进行了详细证明.

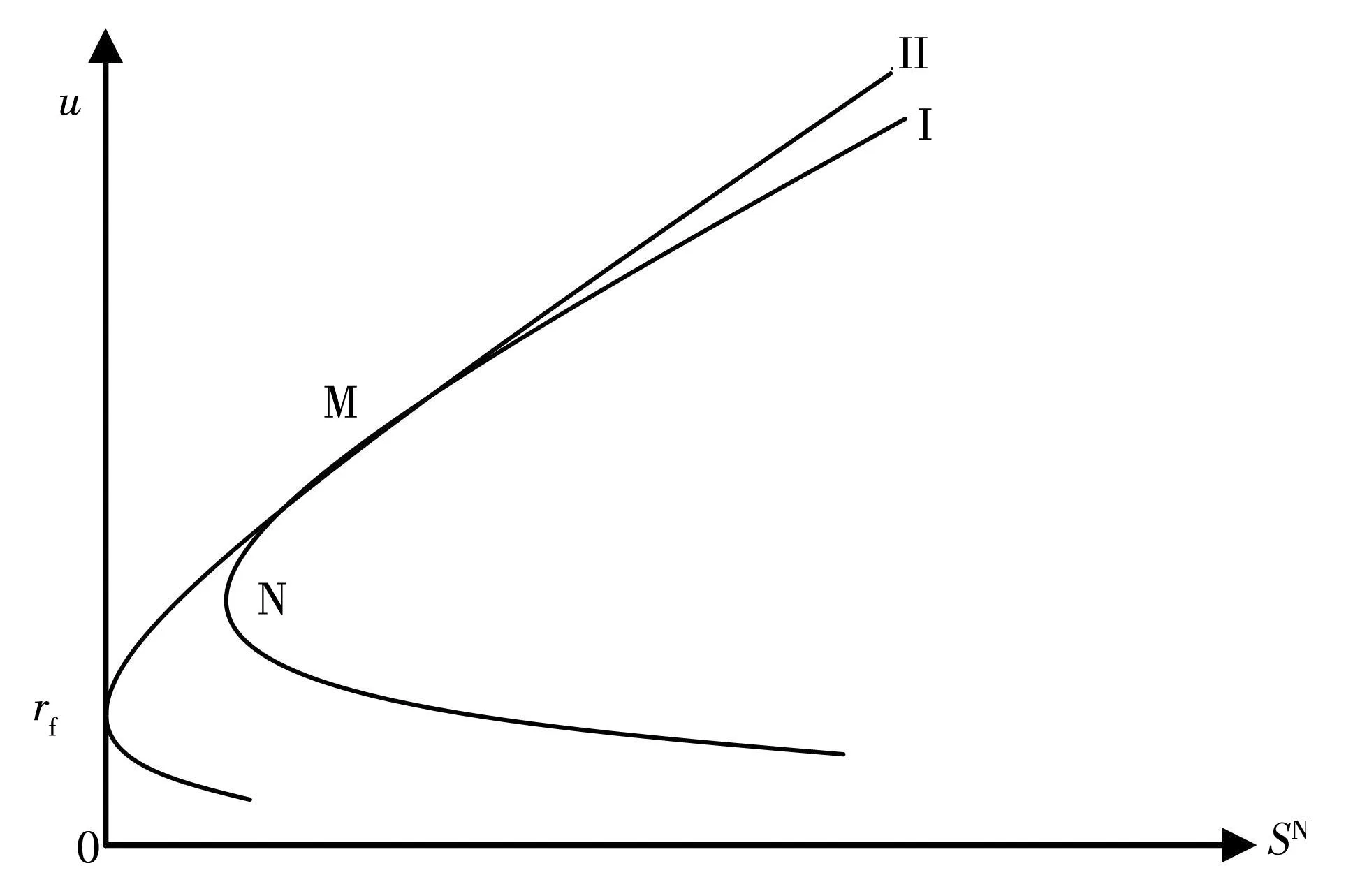
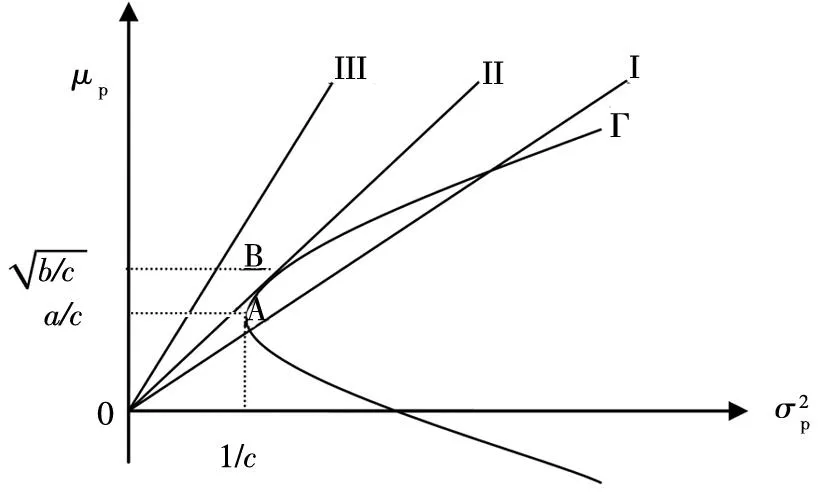
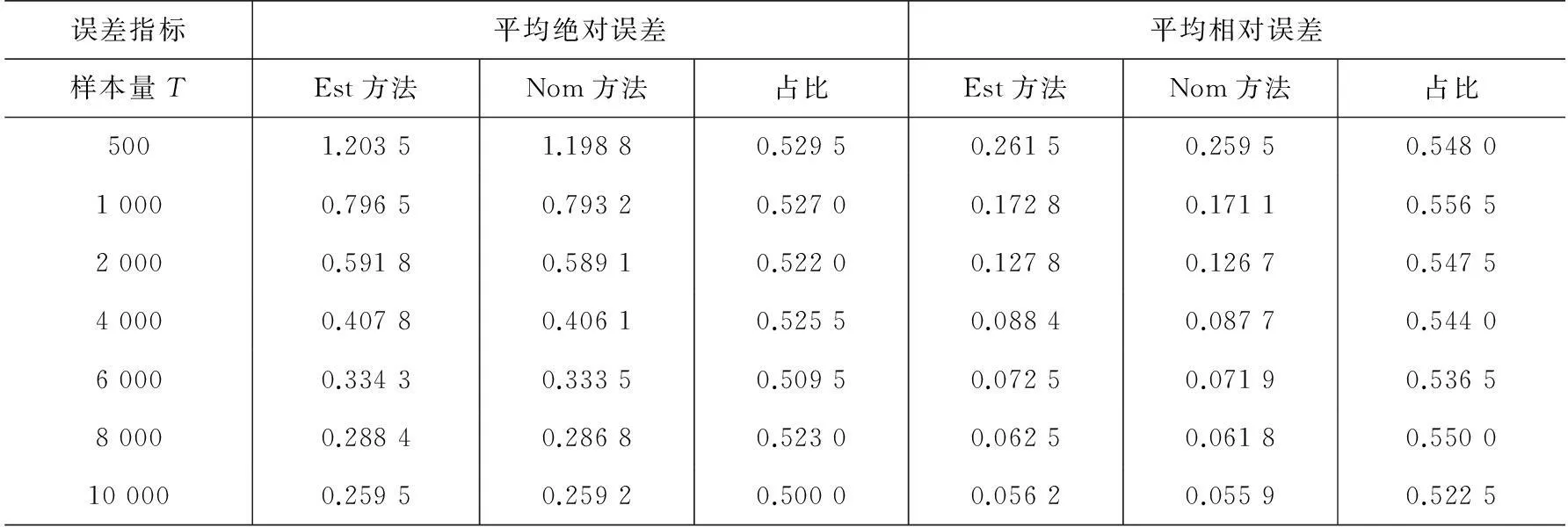
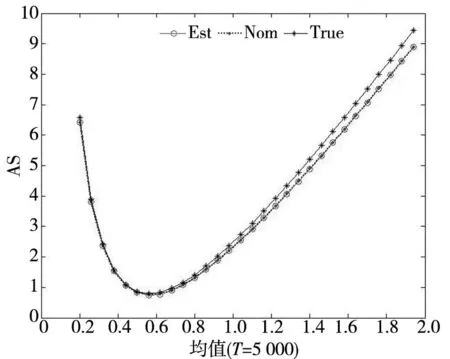
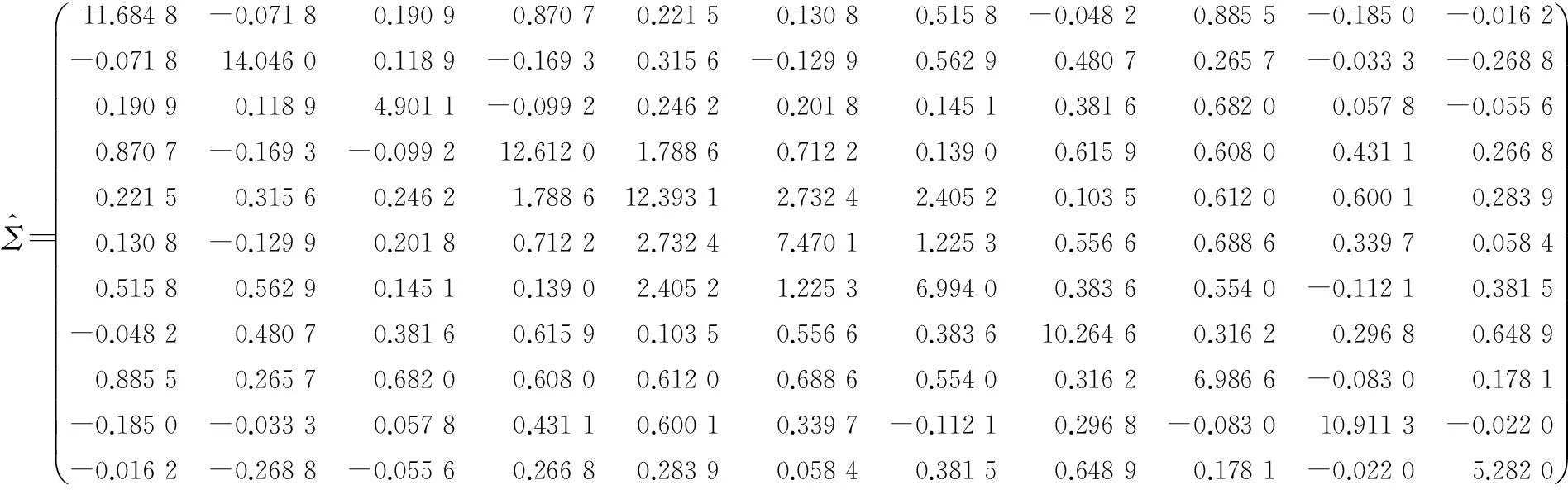
性质1AS指标具有随机占优单调性，即x1一阶(或二阶)随机占优x2，则Sx1

性质2AS指标具有正奇次性，即对任意t>0和满足正则条件的变量x，有Stx=tSx.

性质3若两个赌局的净收益变量x1,x2相互独立，则两个赌局加和的净收益变量x1+x2的风险在x1和x2的风险之间，即min{Sx1,Sx2}≤Sx1+x2≤max{Sx1,Sx2}.

推论如果两个赌局各自的净收益变量x1, x2独立同分布，则它们具有相同的风险值，即Sx1=Sx2，并且二者加和的风险值Sx1+x2=Sx1=Sx2=S.

性质4AS指标具有次可加性，即对任意两个赌局的净收益变量x1和x2，有Sx1+x2≤Sx1+Sx2.

2资产和资产组合的AS指标

金融市场上的投资组合选择是典型的不确定条件下的决策过程，其产生的收益为一随机变量.因此，AS指标可用来度量风险资产与资产组合的风险.Homm和Pigorsch[15]及Chen等[16]采用AS指标度量金融资产的风险，研究了基金表现测度和风险对冲等问题.假设投资者的投资总额为ω、效用函数为CARA，某金融资产的收益率为r，存在某γ*，使式子

成立.令Sωr=1/γ*，上式可化为

根据正齐次性可得Sωr=ωSr.可见，资产收益率的风险与投资者所拥有的财富无关，由其收益率的分布唯一决定，投资者面临的总风险与其投资额呈线性关系.所以下面将投资者的财富标准化为1.

假设市场上存在n(n≥2)种风险资产，第i种资产的收益率为ri，则r=(r1,r2,…,rn)′为n种资产的收益率向量*如无特殊说明所有向量都定义为列向量，符号“′”表示转置..设w=(w1,w2,…,wn)′为投资者在n种资产上的头寸，w′r为投资组合的收益率.根据式(1)，该组合的风险Sw可通过下式求出*按照前文定义组合的AS指标应记为Sw′r，但为了简洁在不引起混淆的情况下，简写为Sw.

(2)

令z∶=w′r/Sw，B(w)∶=E[exp(-z)r]，C(w)∶=E[exp(-z)w′r].

定理2如果C(w)<0，则Sw是组合头寸w的凸函数.

证明见附录.

3正态分布下的Mean-AS模型

其中u为给定的收益率.可以证明不等式约束在最优解处是紧的.

容易看出，在正态分布假设下优化问题(P1)的最优策略与均值-方差模型的最优策略是相同的.令a=e′Σ-1μ,b=μ′Σ-1μ,c=e′Σ-1e,d=bc-a2，利用拉格朗日方法，容易得到上述问题的最优解为

w*=d-1[(cu-a)Σ-1μ+(b-au)Σ-1e]

把w*代回目标函数，可得n种风险资产投资组合的组合边界为

(3)

若市场引入一无风险资产，其收益率为rf，其它条件不变，则组合的收益率为w′r+(1-w′e)rf，服从正态分布N(w′μ+(1-w′e)rf,w′Σw)，相应的均值-AS模型为

类似分析，可得问题的解析解为

(4)

图1　均值-AS模型下的组合边界

命题1在正态分布假设和均值-AS模型框架下，模型(P1)和(P2)所得的曲线只有1个交点，该点的坐标记为(S*,u*)，则(i)当a<0或a>0且rf∈(a/c,b/a)时，u*<0；(ii)当a>0且rf∈(0,a/c)∪(b/a,∞)时，u*>0.

此式可化简为

显然，方程的判别式为

故两曲线只有1个交点.又因为

而

当a<0时，arf-b<0且crf-a>0，所以drf-ah>0，从而得u*<0；当a>0时，由bc-a2>0，可得a/c

如果00；如果a/ca且arf0，进而u*<0；如果rf>b/a，则crf>a且arf>b，此时drf-ah<0，进而u*>0.

命题2在正态分布假设和均值-AS模型框架下，当a>0且rf∈(0,a/c)时，含无风险资产的有效边界与不含无风险资产的有效边界相切.当a>0且rf∈(b/a,∞)时，含无风险资产的组合边界与不含无风险资产的组合边界相切，但有效边界相离.当a<0或a>0且rf∈(a/c,b/a)时，含无风险资产的组合边界与不含无风险资产的组合边界相离.

证明由命题1知，模型(P1)和(P2)所得曲线存在唯一交点(S*,u*).又因为

在交点(S*,u*)处曲线斜率相同，所以模型(P1)和(P2)所得曲线在交点处相切.

由命题1可知，当a>0 且rf∈(0,a/c)时，u*>0.又因为

所以此时u*>uminS，即切点在有效边界上.

可见此时含无风险资产的有效边界与不含无风险资产的有效边界相切(即图1曲线I与曲线II相切).

同理可证，当a>0且rf∈(b/a,∞)时，u*>0，且u*0且rf∈(a/c,b/a)时，根据命题1，u*<0，所以由模型(P1)和(P2)所得曲线的唯一交点(S*,u*)位于第三象限，第一象限内的组合边界没有交点，所以，含无风险资产的组合边界与不含无风险资产的组合边界相离.

命题3在正态分布假设下，均值-AS模型的有效边界是均值-方差模型有效边界的子集.

由模型(P1)和(P2)可知，在正态分布假设下均值-AS模型与均值-方差模型的最优组合相同，它们得到的组合边界也相同.只是在不同坐标系(即不同的风险度量)下曲线形状不同而已.如何在均值-方差坐标系下找到最小AS的组合呢？众所周知，经典的均值-方差模型下的曲线表达式为[17]

(5)

图2　均值方差平面下的组合边界与等AS线

4一般分布下的Mean-AS模型

在正态分布下，AS指标可表示成均值与方差的函数，只要知道n种资产收益率的均值向量和协方差阵，就可以得到组合边界的解析表达式.但在一般分布下，由于事先并不知道分布特征，无法得到AS指标的解析式*Schulze[11]给出了指数分布、泊松分布、Gamma分布、方差-Gamma分布等情形下AS指标的解析表达式..此外，即使在正态分布下，往往并不知道n种资产收益率真实的均值向量和协方差阵，实践中，通常需要利用样本数据对其进行参数估计.本节中，考虑在一般分布下，没有AS指标的解析式时如何利用样本数据得到均值-AS模型的组合边界估计.为此，下文探讨在不做任何分布假设前提下利用样本数据对AS指标进行估计，得到AS指标的矩估计式，然后将AS指标的矩估计式嵌入均值-AS模型，实现风险估计与风险优化同步进行.

(6)

(7)

对式(7)两边关于w求导，可得

(8)

建立拉格朗日函数

可得到相应的一阶条件为

相应的Hessian矩阵为

(9)

将式(9)两边对w求导，并令

可得

(10)

将式(10)两边关于w求导，并令

可得

(11)

该模型的求解方法和步骤与模型(P3)相同.

5蒙特卡洛模拟

前两节在理论上讨论了正态分布和一般分布下均值-AS模型组合边界的估计方法.为验证前两节估计方法的准确性，本节基于蒙特卡洛模拟方法给出一些数值算例.蒙特卡洛模拟的思想是：事先设定一个真实的分布，基于该分布生成随机变量的样本，然后假设不知道真实分布的情况下，利用前文提出的估计方法和生成的样本数据来估计均值-AS模型的组合边界，并与真实的组合边界进行比较，来验证前文所提估计方法的准确性.到目前为止，只能得到资产收益率向量服从多维正态分布时的真实组合边界，所以为了比较的方便，以下模拟假设真实分布为多维正态分布.样本生成过程采取Cholesky分解法.Cholesky分解法的思路是：假设n(n≥2)种资产收益率向量r服从n维正态分布N(μ,Σ)，协方差阵Σ正定，则由Cholesky分解得Σ=Q′Q，Q为上三角矩阵.令r=μ+ Q′ε，ε为n维标准正态分布，通过简单推导可知r～N(μ,Σ)，这样通过ε就可以生成多维正态分布N(μ,Σ)的随机数.假设市场上存在4种风险资产*4种以上资产情况类似讨论，后文的实例分析将资产数量拓展至更多维.，它们真实的均值向量和协方差阵为*需要说明的是，这里的数据是虚拟数据，数据的量纲(或单位)可以是任意的，如果是金融资产的收益率数据，量纲可以取%(月收益率)或者‰(日收益率).μ=(0.5 0.8 1.0 1.2)′和

将真实的均值向量μ和方差阵Σ代入式(3)就可得到真实的均值-AS曲线.以下将假设真实分布未知，利用本文的估计方法对均值-AS曲线进行估计.

模拟1不含无风险资产时，均值-AS模型下的组合边界估计.

(12)

第3步重复前两步骤3 000次，即进行3 000次蒙特卡洛模拟.然后将3 000次得到的误差指标Ae和Re进行平均，得到平均绝对误差和平均相对误差.为了比较，定义了如下占比指标：在3 000次的重复模拟中，Est方法误差大于Nom方法误差的次数除以3 000.

第4步分别取样本容量T=1 000，2 000，4 000，6 000，8 000，10 000，重复前3个步骤.最后得到两种估计方法的误差表(见表1)

Table 1 Estimation error of Est method and Nom method

误差指标平均绝对误差平均相对误差样本量TEst方法Nom方法占比Est方法Nom方法占比5001.20351.19880.52950.26150.25950.548010000.79650.79320.52700.17280.17110.556520000.59180.58910.52200.12780.12670.547540000.40780.40610.52550.08840.08770.544060000.33430.33350.50950.07250.07190.536580000.28840.28680.52300.06250.06180.5500100000.25950.25920.50000.05620.05590.5225

从表1可以看出：1)随着样本量的增加，矩估计方法得到的组合边界，其平均相对误差和平均绝对误差都在下降，这是矩估计的大样本性质.2)随着样本容量的增加，正态分布假设下得到的组合边界的平均相对误差和平均绝对误差也在下降，这是因为生成数据的原始分布就是正态分布，本文这里做了正确的分布假设，在正态分布假设下，AS指标由均值和协方差阵唯一决定.随着样本量增加，样本均值和样本协方差收敛于真实的均值和方差阵，从而优化模型的组合边界收敛于真实边界.3)虽然矩估计方法和正态分布假设下得到的组合边界都趋向于真实组合边界，但是矩估计方法不做任何的分布假设，而后一种方法做了正态分布假设，而这个假设在本例中正好是对的.如果这个假设是错误的(实际上金融市场上的数据通常都呈非正态特征)，将会产生模型设定风险，这时不做任何分布假设的矩估计方法更加有效.4)占比一栏的数据说明，在3 000次的重复模拟中，矩估计方法的误差大于正态假设下误差的占比在50%左右(略高于50%)，这说明两种方法误差大小不分伯仲.从平均绝对误差值和平均相对误差值来看，两种估计方法的误差值大多数都在小数点后的第3位才开始有所差异.所以虽然矩估计方法不做任何分布假设，却能够得到如同做了正确分布假设几乎一样的效果.

图3直观地显示，随着样本容量的增加，两种方法得到的组合边界都趋向于真实的组合边界.另外颇为意外的特征是：无论样本容量为多少，两种估计方法得到的组合边界几乎重叠，出现这种现象的原因是两种估计方法都是利用同样的样本数据进行估计，两种估计方法共同受到样本质量好坏的直接影响.另外，这也进一步说明了不做分布假设的矩估计方法能够得到如同做了正确分布假设几乎一样的效果.

模拟2含无风险资产时，均值-AS模型下的组合边界估计.

从表2，可得到所有表1上得到的结论，说明引入无风险资产之后，基于矩估计方法的模型和算法同样适用.图4显示了随样本容量增加时，矩估计方法和正态分布假设方法得到的组合边界都趋于真实的组合边界.虽然图4显示含无风险资产的组合边界接近于直线，但从正态分布假设下真实均值-AS曲线的表达式(4)来看，这的确不是一条直线，而是曲线.

误差指标平均绝对误差平均相对误差样本量TEst方法Nom方法占比Est方法Nom方法占比5000.22770.21600.57350.14560.13750.576510000.15760.15050.55400.10110.09620.555530000.09000.08620.55450.05800.05530.555050000.06930.06660.55900.04470.04280.564580000.05460.05240.54450.03530.03370.5455100000.05040.04760.56550.03250.03060.5680

6实例分析

本节选取我国A股市场股票的日对数收益率数据进行实例分析，在理论分析中，假设风险资产收益率的均值为正，这样才能保证它们各自的AS指标有解.为保证优化过程能够顺利进行，选取了日收益率的样本均值大于零的股票来进行实证分析.本文选择的股票是：深物业A、深深宝A、云南白药、铜陵有色、中金岭南、合肥百货、格力电器、罗牛山、承德露露、新希望和青岛啤酒共11只股票，数据期间为2007-01-01～2012-12-31.由于在某些交易日，有些股票因各种原因会停盘，所以必须选出那些每只股票都有交易的交易日收盘价数据，经过删减和匹配处理后，每只股票的可用日对数收益率数据为1 278个.由于日对数收益率数据都很小，为了方便，把所有的日对数收益率数据都乘以100，容易算得11只股票日对数收益率数据的样本均值和样本协方差阵分别为

图5我国均值-AS曲线估计(左图：Est方法，右图：Nom方法)

Fig. 5 Mean-AS curve estimation of Chinese share market (left: Est method, right: Nom method)

7结束语

本文基于诺贝尔经济学奖得主Aumann与其合作者Serrano提出的新风险度量指标AS，构建了均值-AS模型.本文得到了正态分布假设下均值-AS模型组合边界的解析式，并深入探讨了正态分布下该模型组合边界和有效边界特征.在不做任何分布假设下，利用矩估计方法对AS指标进行估计，得到AS指标的矩估计式，然后将矩估计式嵌入均值-AS模型，并基于迭代算法对该模型进行求解，得到一般分布下均值-AS曲线的估计.模拟结果表明本文的矩估计算法虽不做任何的分布假设，但能得到与做了正确分布假设一样的精度.

AS是最近提出来具有众多优点的新风险度量指标，对它的研究和认识还有待进一步深入，下一步的研究可考虑，在正态分布假设下基于均值-AS模型的资产定价问题，以及一般分布下基于AS的风险对冲和风险管理问题以及动态投资组合优化问题等.

参 考 文 献：

[1]Diamond P A, Stiglitz J E. Increases in risk and in risk aversion[J]. Journal of Economic Theory, 1974, 8(3): 337-360.

[2]Arrow K J. Aspects of the Theory of Risk-Bearing[M]. Helsinki: Yrjö Jahnssonin Säätiö, 1965.

[3]Arrow K J. Essays in the Theory of Risk-Bearing[M]. Amsterdam, London: North-Holland Publishing Company, 1971.

[4]Pratt J W. Risk aversion in the small and in the large[J]. Econometrica: Journal of the Econometric Society, 1964, 32(1/2): 122-136.

[5]Markowitz H. Portfolio selection[J]. The Journal of Finance, 1952, 7(1): 77-91.

[6]Aumann R J, Serrano R. An economic index of riskiness[J]. Journal of Political Economy, 2008, 116(5): 810-836.

[7]Hadar J, Russell W R. Rules for ordering uncertain prospects[J]. American Economic Review, 1969, 59(1): 25-34.

[8]Hanoch G, Levy H. The efficiency analysis of choices involving risk[J]. The Review of Economic Studies, 1969, 36(3): 335-346.

[9]Rothschild M, Stiglitz J E. Increasing risk: I. A definition[J]. Journal of Economic Theory, 1970, 2(3): 225-243.

[10]Homm U, Pigorsch C. An operational interpretation and existence of the Aumann-Serrano index of riskiness[J]. Economics Letters, 2012a, 114(3): 265-267.

[11]Schulze K. Existence and computation of the Aumann-Serrano index of riskiness and its extension[J]. Journal of Mathematical Economics, 2014, 50(1): 219-224.

[12]Schreiber A. An Economic Index of Relative Riskiness[R]. Jerusalem: Hebrew University, 2012.

[13]Foster D P, Hart S. An operational measure of riskiness[J]. Journal of Political Economy, 2009, 117(5): 785-814.

[14]Bali T G, Cakici N, Chabi-Yo F. A generalized measure of riskiness[J]. Management Science, 2011, 57(8): 1406-1423.

[15]Homm U, Pigorsch C. Beyond the sharpe ratio: An application of the Aumann-Serrano index to performance measurement[J]. Journal of Banking & Finance, 2012b, 36(8): 2274-2284.

[16]Chen Y T, Ho K Y, Tzeng L Y. Riskiness-minimizing spot-futures hedge ratio[J]. Journal of Banking & Finance, 2014, 40(3): 154-164.

[17]Levy H. Stochastic dominance and expected utility: Survey and analysis[J]. Management Science, 1992, 38(4): 555-593.

[18]姚京, 李仲飞. 基于VaR的金融资产配置模型[J]. 中国管理科学, 2004, 12(1): 8-14.

Yao Jing, Li Zhongfei. The asset allocation model based on VaR[J]. Chinese Journal of Management Science, 2004, 12(1): 8-14. (in Chinese)

附录：

定理1的证明

图A-1　f(α)的函数图像

定理2的证明

式(2)两边分别对w求导可得

再对上式关于w′求导有

又因为

令D(w)=C(w)r-B(w)(w′r)，经化简可得

进而可得

定理3的证明

Asset allocation based on mean-AS model

ZENGYan1,HUANGJin-bo2

1. Lingnan (University) College, Sun Yat-Sen Universtiy, Guangzhou 510275, China;2. School of Finance, Guangdong University of Finance & Economics, Guangzhou 510320, China

Abstract:The AS index is a new risk measure put forward recently by Aumann and Serrano who are inspiredby the theory of choice under uncertainty.It has many advantages over other risk measures andattracts many scholars. In this paper, we consider an asset allocation problem with the Mean-AS model under normal distribution and general distribution assumption, respectively. In the former case, we obtain an analytical expression of portfolio frontier and thoroughly discuss the characteristics of portfolio frontier. In the latter case, we embody the AS moment estimator into the Mean-AS portfolio optimization model and implement risk estimation and portfolio optimization simultaneously. Under very mild conditions, we prove that the Mean-AS model is a convex optimization problem and an iterative algorithm can be designed to obtain its numerical solution. Monte Carlo simulation results show that the Mean-AS model and our algorithm are accurate and effective. Finally, an empirical case of stock portfolio in Chinese A-stock market is illustrated.

Key words:mean-AS model; AS index; portfolio frontier; moment estimator

中图分类号:F830.9； F224.7； O224

文献标识码:A

文章编号:1007-9807(2016)02-0095-14

作者简介:曾燕 (1984—)， 男， 江西吉安人， 博士， 副教授. Email: zengy36@mail.sysu.edu.cn

基金项目：国家自然科学基金重点资助项目(71231008)； 国家自然科学基金资助项目(71201173； 71571195)； 广东省自然科学杰出青年基金资助项目(2015A030306040)； 广东省自然科学基金资助项目(S2013010011959)； 广州市哲学社会科学“十二五”规划资助项目(15Q20)； 中国博士后科学基金资助项目(2014M562246).

收稿日期：① 2014-04-11；

修订日期：2014-11-20.