多响应稳健参数设计的贝叶斯建模与优化①

汪建均， 马义中， 欧阳林寒， 孙金生， 刘　健

(1. 南京理工大学经济管理学院， 南京 210094； 2. 南京理工大学自动化学院， 南京 210094)



多响应稳健参数设计的贝叶斯建模与优化①

汪建均1, 2， 马义中1， 欧阳林寒1， 孙金生2， 刘健1

(1. 南京理工大学经济管理学院， 南京 210094； 2. 南京理工大学自动化学院， 南京 210094)

摘要：针对多响应稳健参数设计问题，在贝叶斯统计建模的框架下，结合质量损失函数和后验概率方法构建了一种新的优化模型.该方法不仅运用后验概率方法评估了各响应落在规格限内的期望概率(即优化结果的可靠性)，而且运用质量损失函数度量了多变量过程的稳健性.此外，进一步地结合实例讨论了期望概率对优化结果的影响、联合概率与边缘概率之间的关系以及如何获得质量损失与后验概率之间的最佳平衡点.研究结果表明：所提方法能够在优化过程中较好地兼顾多元过程的稳健性和优化结果的可靠性，从而为实现多响应稳健参数设计提供了各方面(如多元过程的稳健性、优化结果的可靠性)均较满意的优化结果.

关键词：贝叶斯分析； 多响应； 后验概率； 质量损失函数； 稳健参数设计

0引言

稳健参数设计在产品或过程的质量改进活动中得到了广泛应用，有效地提高了产品或过程的质量，产生了巨大的经济效益.随着顾客需求层次的多样化以及产品复杂程度的日益提高，在产品或过程的质量设计中往往需要考虑多个质量特性(即多响应)，因此多响应稳健参数设计在持续性质量改进活动中显示出越来越重要的地位与作用[1].在多响应稳健参数设计的研究中，通常会涉及到一系列的研究问题,大体上可以归纳为如下3个方面的研究内容[2, 3]：第1，指标构建.如何构建有效的指标以合理地度量多响应系统的稳健性以及多响应之间的相关性；第2，模型构建.如何在过程模型的构建中考虑模型的预测性能以及多目标优化时的冲突；第3，参数优化.如何选择合适的优化算法以获得模型参数的全局优化解和稳健解，同时还需要进一步地评估优化结果的可靠性，即考虑响应观测值落在产品规格限内的概率.

针对多响应稳健参数设计所存在的问题，近年来国内外学者提出了各种各样的研究方法，归纳起来主要包括以下几种常见的方法[3]：满意度函数法、马氏距离法、多元质量损失函数、贝叶斯后验概率法等.在上述方法之中，满意度函数法以其简洁实用、易于操作，在工程实践中得到了广泛应用.然而，一些研究者[4]指出，满意度函数法忽视了响应之间相关性，因而在多响应之间存在高度的相关性或具有不同的方差结构时可能难以获得合理的参数设计值.此外，传统的满意度函数未考虑响应的预测性能及其优化结果的可靠性，因此在某些情况下根据满意度函数所获得的研究结果将很不可靠[5, 6].马氏距离法虽然考虑了响应之间的方差-协方差结构，但是当各个响应之间存在明显的冲突时，该方法的效果将会受到很大影响.此外，马氏距离法也忽视了响应的预测性能及其优化结果的可靠性等问题[7].Ko等[8]结合Pignatiello[9]和Vining[10]所提出的多元质量损失函数，既考虑了过程的稳健性、多响应之间的相关性，同时还考虑了响应的预测性能，提出了新的多元质量损失函数方法.该方法要求对每轮试验进行完全重复，以便运用似不相关回归(seemingly unrelated regressions, SUR)方法估计响应的方差-协方差矩阵.当响应之间存在高度的相关性时，SUR方法能够给出更为精确的模型估计，提高模型的拟合效果与预测性能，但SUR对样本量具有较高的要求[11].此外，该方法未考察预测响应值落在规格限内的概率，从而无法对稳健优化的结果进行有效的可靠性评估.Peterson[12]曾指出运用满意度函数或质量损失函数等指标进行多响应稳健参数设计时，其响应预测值落在规格限的概率可能相当低，甚至无法令人接受.

近年来，如何评估多响应稳健参数设计优化结果的可靠性引起一些学者的关注和重视.Chiao和Hamada[13]在多响应优化设计中提出一种评估优化结果可靠性的新方法.该方法通过估计多变量正态响应满足顾客设定条件的概率来评估优化结果的优劣，其主要优势在于该方法能够有效地考虑响应数据之间的方差-协方差结构，并且适用于异方差以及含有噪声变量的回归模型.然而，该方法也存在一些不足之处，最主要的问题是该方法在优化过程中忽视了模型参数的不确定性.为此，Peterson[12]提出了贝叶斯的后验概率方法.该方法在贝叶斯建模与优化过程中考虑了试验数据之间的相关结构、过程分布的变化以及模型参数的不确定性[14]，然后利用蒙特卡洛(Monte Carlo)模拟方法从多响应的后验预测分布中进行抽样，从而计算出多响应的抽样值落在规格限内的概率.Miro-Quesada等[15]扩展Peterson[12]的研究工作，在多响应过程模型构建之中考虑了噪声因子的影响.此外，Peterson等[16]考察了多响应之间存在不同协方差的问题，进而结合多变量的似不相关回归模型改进了以往的研究工作.Robinson等[17]首先对广义线性混合模型(generalized linear mixed models, GLMM)进行贝叶斯分析，然后结合贝叶斯后验概率方法对裂区试验设计进行了参数优化.该方法不仅适用于正态响应，也适用于非正态响应的参数优化设计问题.然而，上述方法过分关注响应预测值或抽样值落在规格限内的概率，却忽视了多元过程的稳健性.事实上，在很多情况下仅考虑优化结果的可靠性所获得的参数设计值，其可靠性结果往往令人满意，但其质量损失却相当大.因此，如何在统一的框架下全面地考虑多响应稳健参数设计所涉及的一系列问题(如多响应之间的相关性、多目标优化的冲突性、多元过程的稳健性以及研究结果的可靠性等问题)，尤其是同时考虑稳健性与优化结果的可靠性，目前还缺乏行之有效的研究方法.

针对多响应稳健参数设计问题，本文拟在贝叶斯多元回归模型的统一框架下，首先根据贝叶斯后验样本计算出响应预测值的均值向量与方差-协方差矩阵，在此基础上构建基于改进的多元质量损失函数，从而获得相应的优化目标函数；然后通过贝叶斯后验概率方法获得响应抽样值落在规格限内的概率，并以该概率不低于某个期望的目标值为约束条件；最后运用混合遗传算法对具有非线性约束的目标函数进行参数优化，从而获得理想的参数设计值.

1多元质量损失函数

日本著名的质量工程专家Taguchi认为“质量特性一旦偏离其设计目标值，就会造成质量损失，偏离越远，损失越大”.为了近似地描述产品质量特性y偏离目标值T所造成的质量损失，Taguchi定义了单个质量特性的二次损失函数

L(y)=k(y-T)2

(1)

其中k为与y无关的常数，通常由功能界限和丧失功能的损失来确定.为了进一步量化质量损失，Taguchi提出了期望损失函数的概念，即用L(y)的数学期望L(y) E(L(y))表示期望质量损失，其表达式为

E(L(y))=kE(y-T)2

=kE(y-Ey+Ey-T)2

=k[σ2+(Ey-T)2]

(2)

从式(2)可知，为了最大限度地减少产品或过程的质量损失，应该在保持过程输出均值Ey接近设计目标值的情况下，尽可能地减少过程输出的波动，即响应y的方差σ2.Pignatiello[9]扩展了Taguchi二次损失函数，提出了多元质量损失函数

L(y(x),θ)=(y(x)-θ)TC(y(x)-θ)

(3)

其中y(x)为p个响应y所构成的p×1向量，θ为目标值所构成的p×1向量，C为反映过程经济的成本矩阵.针对式(3)取数学期望得到期望质量损失，其表达式为

E[L(y(x),θ)]=(E[y(x)]-θ)T×

C(E[y(x)]-θ)+

trace[CΣy(x)]

(4)

其中Σy(x)是p×p的方差-协方差矩阵.上述式(4)的右边包含了两个部分，第1部分为偏差成分，第2部分为方差成分.而方差成分反映了过程的稳健性，随着方差成分减少，过程的稳健性将会提高.

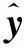
(5)

根据上述质量损失函数的定义，其期望损失函数定义如下

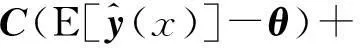
(6)

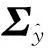
(7)

(8)

其中εnew(x)为随机误差项.针对式(7)和式(8)，得到期望质量损失函数如下

(9)

式(9)右边包含了3部分，分别反映了过程预测值偏离目标值的偏差(Lbias)、过程的预测性能(Lpred)以及过程的稳健性(Lrobust).关于式(9)的详细推导过程可参考文献[8].

2结合多元质量损失与贝叶斯后验概率的多响应稳健参数设计

2.1多元回归模型的贝叶斯分析

在多响应稳健参数设计中，若存在p个质量特性和q个因子效应，则多响应曲面回归模型可假设为

y=Bz(x)+e

(10)

其中B为p×q的回归系数矩阵；z(x)为关于因子效应x的q×1向量；向量e服从均值向量为0、方差-协方差矩阵为Σ的正态分布.

为了说明和解释模型参数B和Σ的不确定性，本文拟在多响应曲面回归模型的框架下结合贝叶斯方法进行建模与优化分析，从而系统地解决多响应稳健参数设计所面临一些关键问题.在参数θ无任何先验信息时，无信息先验p(θ)可以用Fisher信息阵的行列式求平方根来表示[18]，即

(11)

针对多元回归模型的参数θ=(β，Σ)，结合上述公式利用Fisher信息阵可以分别推导出参数B和Σ的Jeffreys先验分布[19]

(12)

若假设参数B和Σ是相互独立的，则参数B和Σ的联合先验分布满足

(13)

在给定试验数据(data)和试验因子x的条件下，响应y的贝叶斯后验概率密度函数为

(14)

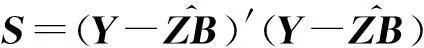
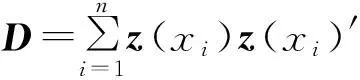
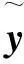
(15)

根据式(15)可以运用蒙特卡洛模拟方法计算出响应抽样值落在规格限A内的概率，即结合贝叶斯后验概率方法考察优化结果的可靠性

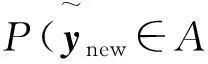
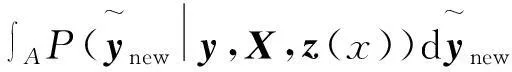
(16)

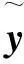
(17)

根据式(17)的结果，运用式(9)可以计算出多响应系统的期望质量损失，从而有效地刻画多元过程的稳健性.

2.2基于贝叶斯后验样本的多响应稳健参数优化

1)首先模拟服从均值为0，方差-协方差均值为H-1的多变量正态分布的随机变量W，即W～N(0, H1)；

3)最后根据多变量t分布的构成，获得响应的最终抽样结果，即

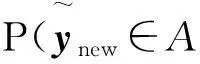
(18)

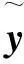
在贝叶斯多元回归模型的统一框架下，结合多元质量损失函数和贝叶斯后验概率方法构建多响应稳健参数设计的优化模型如下

(19)

其中p0为试验者或顾客所期望满足的概率.若在实际应用中缺乏期望概率p0的先验信息，则可以根据式(18)最大化响应值落在规格限内的概率以获得有效的预估值.

考虑到式(19)为高度复杂的非线性优化问题，传统的优化方法往往只能够获得局部的优化解甚至难以找到合适的可行解[20].Jourdan等[21]的研究表明：在解决高度复杂的优化问题时，混合优化算法通常比单一优化算法更有优势.针对多响应的参数优化问题，何桢等[22]曾提出了结合遗传算法与模式搜索的混合优化方法，有效地克服了传统优化算法在处理多约束、多峰以及高度非线性优化问题时的局限性.此后，一些相关研究[23]也表明：充分利用遗传算法的全局搜索能力与模式搜索局部优化的优势，构建二者的混合遗传算法可以弥补上述单一算法的不足，从而能够有效地解决高度复杂的多响应参数优化问题.为此，本文拟采用上述的混合遗传算法对所构建的模型进行参数优化.

在运用混合遗传算法对式(19)进行参数优化时，还需要特别关注如何提高设计程序的运行速度.在利用蒙特卡洛模拟方法对式(19)进行随机抽样时，针对所给定的规格限内某个点，通常需要进行多次反复(如模拟10 000次)模拟抽样以计算贝叶斯多元质量损失函数和贝叶斯后验概率.在这种情形下，若运用迭代循环方法实现上述过程将需要消耗相当长的运行时间.为此，本文采用矩阵化的结构形式(将多次模拟结果通过某个矩阵整体表示)，将极大地提高整个算法程序的运行速度.鉴于篇幅有限，本文未给出相关的Matlab程序，若需要可通过电子邮件与本文第一作者联系.在上述贝叶斯建模的框架下，本文所提方法的整个优化过程可以归纳如下：

步骤1根据所给定的试验数据运用蒙特卡洛模拟方法进行随机抽样，并获得各响应的后验抽样值.

步骤2根据各响应的后验抽样值，计算响应抽样值的均值向量与方差-协方差矩阵.

步骤3根据步骤2的结果构建贝叶斯多元质量损失函数，在具体的优化过程中将其视为最小化的目标函数.

步骤4根据步骤1的结果单独优化贝叶斯后验概率，从而获得其期望概率的预估值.在具体的优化过程中，将贝叶斯后验概率大于或等于其期望概率p0视为所提方法必须满足的约束条件.

步骤5根据上述步骤构建非线性约束的优化模型，应用混合遗传算法对其进行优化，获得最优的参数设计值.

3实例分析

该实例来源于文献[24]，主要研究某聚合物试验的参数设计问题.该聚合物试验具有两个相关的响应，即某聚合物的转化率y1和热活动y2，其中转化率为望大质量特性，而热活动为望目质量特性.影响上述响应的可控因子主要包括：反应时间x1(reaction time)、反应温度x2(reaction temperature)、催化剂的用量x3(amount of catalyst).在该试验中工程师期望获得可控因子的最佳参数组合，从而最大化某聚合物的转化率y1，同时希望维持热活动y2的目标值在57.5的水平上.为此，试验者选择中心复合设计(central composite design, CCD)开展了相关的试验，其试验计划与试验结果如表1所示.

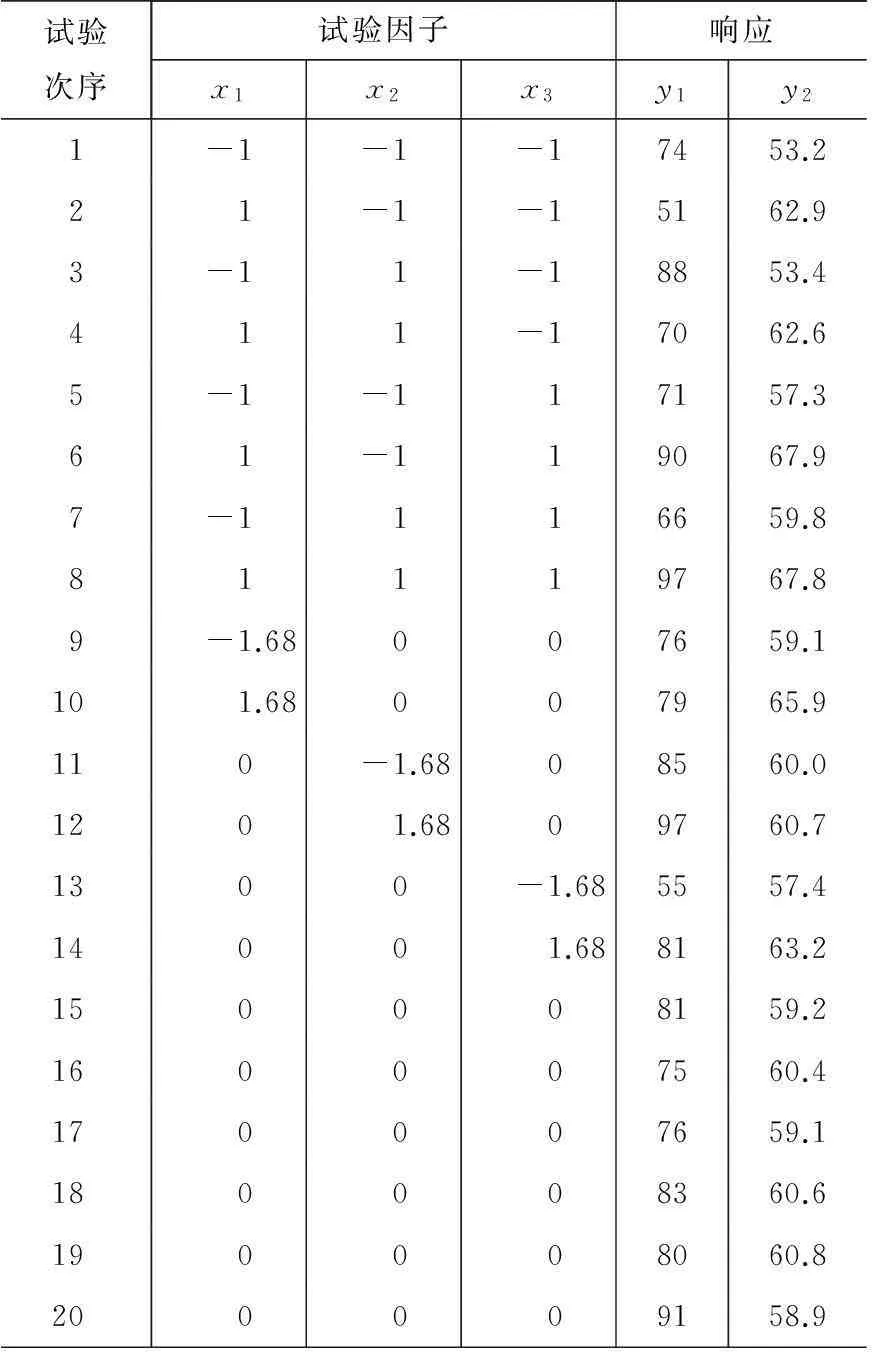
表1　某聚合物试验的试验计划与试验结果

在上述聚合物试验中，转化率的可接受范围为80～100，其目标值θ1假定为100；热活动的可接受范围为55～60，其目标值θ2假定为57.5.在整个试验的分析过程中，假设回归模型式(10)中因子效应所构成的向量为

参考Ko等[8]所给出成本矩阵C的规定，假设成本矩阵C为

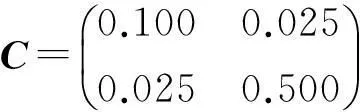
为了获得更为稳健的优化结果，在Matlab优化工具箱中选择遗传算法进行求解，修改种群大小(populationsize)为200，在混合函数(hybridfunction)中选择模式搜索，其他参数选择默认形式，其贝叶斯后验概率的优化结果为0.647 8.为此，根据上述优化结果假设试验者或顾客所期望满足的p0预估值为0.6.在上述约束的条件下，运用混合遗传算法对所构建的优化模型即式(19)进行参数优化，其研究结果如表2所示.根据表2可知，其期望质量损失为14.663 6，同时其响应抽样值落在规格限内的概率，即贝叶斯后验概率为0.602 8.此外，若不考虑贝叶斯后验概率的约束，运用混合遗传算法对运用贝叶斯方法所构建的期望质量损失函数进行优化，其质量损失结果为11.561 3.为了与Ko等所提出的多元质量损失函数进行比较，将其参数值代入到本文所构建的期望质量损失函数和贝叶斯后验概率函数中分别实施模拟运算，其期望质量损失函数结果为11.666 2，贝叶斯后验概率的结果为0.480 6，优化结果如表2所示.

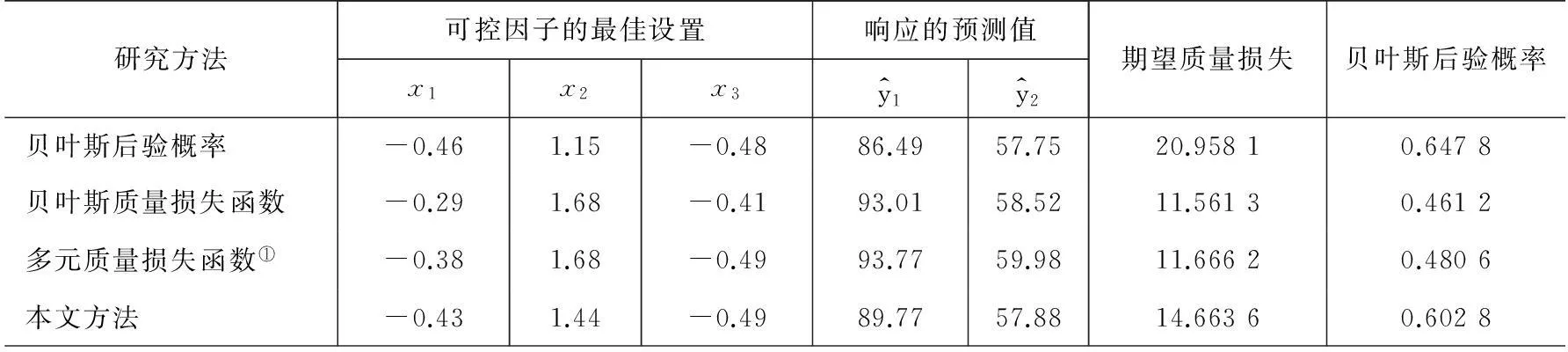
表2　不同研究方法的优化结果

注：①文献[8]的方法.

比较分析表2中不同研究方法的优化结果可知，在上述多响应优化设计的实例中，若仅利用贝叶斯后验概率方法进行参数优化，则其贝叶斯后验概率相对较高，但由于该方法忽视了多元过程的稳健性，因此其期望质量损失(20.958 1)相对较大.若仅利用贝叶斯质量损失函数进行参数优化，则其期望质量损失相对较小，但该方法忽视了对优化结果的可靠性评估，因此其参数所对应的贝叶斯后验概率(0.461 2)相对较低.另外，利用贝叶斯质量损失函数所获得的优化结果与运用多元质量损失函数所获得的优化结果相差不大，从而验证了在贝叶斯多元回归模型的框架下运用蒙特卡洛模拟方法实现多响应稳健参数优化的有效性.与贝叶斯后验概率方法比较而言，运用本文所提方法所获得的期望质量损失将大幅度地减小，而其后验概率却相差不大.与贝叶斯质量损失函数或多元质量损失函数比较而言，运用本文所提方法所获得的后验概率将大幅度地提高，但其期望质量损失的增幅相对较小.因此，运用本文所提方法进行多响应稳健参数设计时能够同时兼顾稳健性与可靠性，从而能够获得各方面(如稳健性、可靠性等)均较满意的优化结果.

4讨论

4.1关于期望概率的分析

在上述试验的优化过程中，如何给出试验者或顾客所期望满足概率p0(产品或过程的响应值落在规格限内的概率)是非常关键的.为此，本文将进一步探讨在不同期望概率下所提方法优化结果的变化与趋势.结合上述的案例结果分析可知：在没有任何约束条件下，若单独以最大化贝叶斯后验概率或者最小化期望质量损失函数为优化目标，则能够获得有关期望概率的上限(0.647 8)和下限(0.461 2).在给定期望概率的区间[0.45, 0.60]内，按照等间隔(0.05)给出4种不同期望概率预估值下的优化结果，如表3所示.

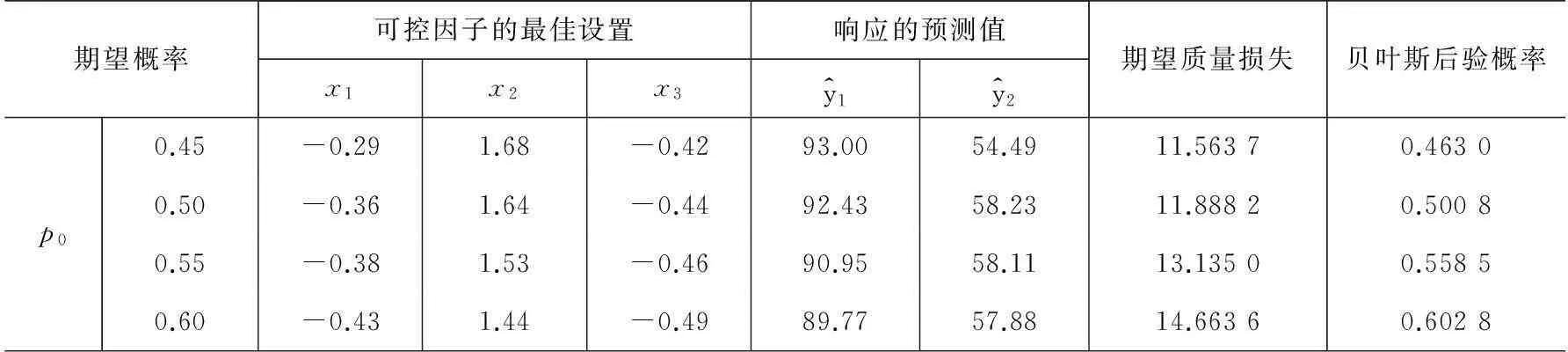
表3　不同期望概率下的优化结果

当假设期望概率p0为0.45时，运用本文所提方法获得的优化结果与最小化期望质量损失函数所获得的优化结果完全一致，这说明当期望概率低于期望下限时，其约束优化问题将退化为无约束的优化问题.若假设期望概率p0为0.65时，运用本文所提方法进行优化分析时其算法程序会提示无可行解.此外，分析表3中不同期望概率的变化情况可知：随着期望概率的逐步变大，其贝叶斯后验概率会随之逐步提高，同时其相应的期望质量损失也会随之逐步增大.因此，如何选择合适的期望概率p0需要结合试验者或顾客的实际需要以及相关的先验知识，同时还需要兼顾到多响应稳健参数设计所需要考虑的一系列问题(如多元过程的稳健性、优化结果的可靠性等)，从而为实现多响应的稳健参数设计提供各方面均较满意的研究方案.

4.2关于联合概率与边缘概率的讨论

4.3关于平衡质量损失与后验概率的讨论

针对质量损失与后验概率如何获得最佳的平衡点, 通常需要结合具体的问题具体分析.以本文的聚合物试验为例，若运用Ko等的多元质量损失函数法，其后验概率的结果(0.461 2)相对较低，在实际生产中将会导致相当高的产品无法满足事先给定的规格要求.在这种情况下，与降低质量损失而言，如何提高其后验概率显得更为重要一些.因此，在实际问题中若后验概率相对较低时，通常会优先考虑如何提高其后验概率.在这种情形下，通常会单独优化贝叶斯后验概率，从而获得后验概率的预估值p0.在保持后验概率不低于其期望概率p0的前提条件下，尽可能地降低质量损失，从而实现降低质量损失和提高后验概率的统一.与贝叶斯后验概率方法比较，本文所提方法大幅度降低了质量损失，但其后验概率则保持与之相近的水平.因此，在贝叶斯后验概率较低时，除了通过改进模型拟合的精度来提高其后验概率之外，运用本文所提方法将能够较好地平衡降低质量损失与提高后验概率两者的矛盾，实现多元过程的稳健性与优化结果的可靠性二者的统一.

另一方面，为了说明在贝叶斯后验概率较高时，如何平衡后验概率与质量损失二者的关系，本文选择了另外一个典型的案例进行分析.该案例最初来源于文献[25]，Peterson[12]曾运用后验概率的方法对该案例进行了深入的研究.该案例主要研究某药品的表面活性剂与乳化剂的混合配比问题，详细的案例情况见Peterson的论文[12].在此，运用本文所提方法对此案例重新进行了分析，并与其他几种方法的研究结果进行了比较，如表4所示.从表4可知：当单独运用贝叶斯质量损失函数进行参数优化时，其参数所对应的贝叶斯后验概率(0.921 9)也较高.若单独运用贝叶斯后验概率进行参数优化时，其后验概率非常接近1.然而，与贝叶斯质量损失函数的优化结果比较而言，其参数所对应的质量损失(6.208 4)则相当高.在这种情况下，通常希望将后验概率维持在较高的水平上，然后尽可能地降低其质量损失.为此，本文选择期望概率p0为0.95，然后运用本文所提方法对该案例进行了优化，从而获得了较小的期望质量损失(0.696 8)和较高的后验概率(0.952 5).

表4　不同研究方法的优化结果

5结束语

在多响应稳健参数设计中，往往会同时考虑多元过程的稳健性、多响应之间的相关性、多目标优化的冲突以及优化结果的可靠性等一系列的问题.本文在贝叶斯回归模型的统一框架下结合了多元质量损失函数与贝叶斯后验概率方法的优势，提出了一种多响应稳健参数设计的新方法.该方法在贝叶斯多元回归模型构建中系统地考虑了多响应之间的相关性、模型参数的不确定性，并结合多元质量损失函数和贝叶斯后验概率方法分别考虑了多元过程的稳健性和优化结果的可靠性.另外，在模型优化过程中，该方法运用矩阵化的结构形式代替了多次模拟循环的过程，从而能够利用蒙特卡洛模拟方法和混合遗传算法快速地计算出最优参数设计点的期望质量损失和贝叶斯后验概率.

需要特别指出的是，本文的研究是建立在回归模型结构不变的基础之上，即在整个分析过程中均假设式(10)中z(x)所包含的因子效应是不变的.如何在贝叶斯多元回归模型的框架下结合贝叶斯模型平均(Bayesian model averaging，BMA)方法[26],以考虑模型不确定性对多响应稳健优化结果的影响，将是未来需要进一步研究的课题之一.另外，本文的研究仅考虑了多响应y的后验密度函数为封闭形式的情况，即在假定参数的先验信息和试验数据的样本信息后能够推导出响应y后验密度函数的具体表达式.然而，在相当多的情况下研究者无法直接获得响应y后验密度函数的具体表达式[17].如何结合马尔科夫链蒙特卡洛(Markov chain Monte Carlo，MCMC)方法动态模拟响应y的后验分布函数[27, 28]，并在此基础上有效地扩展本文所提方法进行多响应的稳健参数设计，也是未来需要进一步地深入探索和研究的课题之一.

参 考 文 献：

[1]汪建均, 马义中, 翟云焕. 相关多质量特性的优化设计[J]. 管理工程学报, 2011, 25(2): 66-73.

Wang Jianjun, Ma Yizhong, Zhai Yunhuan. Optimization design of correlated multiple quality characteristics[J]. Journal of Industrial Engineering and Engineering Management, 2011, 25(2): 66-73. (in Chinese)

[2]Ardakani M K, Wulff S S. An overview of optimization formulations for multiresponse surface problems[J]. Quality and Reliability Engineering International, 2013, 29(1): 3-16.

[3]Murphy T E, Tsui K L, Allen J K. A review of robust design methods for multiple responses[J]. Research in Engineering Design, 2005, 15(4): 201-215.

[4]何桢, 宗志宇, 孔祥芬. 改进的满意度函数法在多响应优化中的应用[J]. 天津大学学报, 2006, 39(9): 1136-1140.

He Zhen, Zong Zhiyu, Kong Xiangfen. Application of improved desirability function method to the multi-reponse optimization[J]. Journal of Tianjin University, 2006, 39(9): 1136-1140. (in Chinese)

[5]He Z, Wang J, Oh J, et al. Robust optimization for multiple responses using response surface methodology[J]. Applied Stochastic Models in Business and Industry, 2010, 26(2): 157-171.

[6]He Z, Zhu P F, Park S H. A robust desirability function method for multi-response surface optimization considering model uncertainty[J]. European Journal of Operational Research, 2012, 221(1): 241-247.

[7]宗志宇, 何桢, 孔祥芬. 多响应优化方法的比较和应用研究[J]. 数理统计与管理, 2006, 26(6): 697-704.

Zong Zhiyu, He Zhen, Kong Xiangfen. Comparison of methods for multiresponse optimization[J]. Application of Statistics and Management, 2006, 26(6): 697-704. (in Chinese)

[8]Ko Y H, Kim K J, Jun C H. A new loss function-based method for multiresponse optimization[J]. Journal of Quality Technology, 2005, 37(1): 50-59.

[9]Pignatiello J J. Strategies for robust multiresponse quality engineering[J]. IIE Transactions, 1993, 25(3): 5-15.

[10]Vining G G. A compromise approach to multiresponse optimization[J]. Journal of Quality Technology, 1998, 30(4): 309-313.

[11]Shah H K, Montgomery D C, Carlyle W M. Response surface modeling and optimization in multi-response experiments using seemingly unrelated regressions[J]. Quality Engineering, 2004, 16(3): 387-397.

[12]Peterson J J. A posterior predictive approach to multiple response surface optimization[J]. Journal of Quality Technology, 2004, 36(2): 139-153.

[13]Chiao C H, Hamada M. Analyzing experiments with correlated multiple responses[J]. Journal of Quality Technology, 2001, 33(4): 451-465.

[14]汪建均, 马义中. 基于GLM 的贝叶斯变量与模型选择[J]. 管理科学学报, 2012, 15(8): 24-33.

Wang Jianjun, Ma Yizhong. Bayesian variable and model selection based on generalized linear models[J]. Journal of Management Sciences in China, 2012, 15(8): 24-33. ( in Chinese )

[15]Miro-Quesada G, Del Castillo E, Peterson J J. A Bayesian approach for multiple response surface optimization in the presence of noise variables[J]. Journal of Applied Statistics, 2004, 31(3): 251-270.

[16]Peterson J, Miro-Quesada G, Del Castillo E. A Bayesian reliability approach to multiple response optimization with seemingly unrelated regression models[J]. Journal of Quality Technology and Quantitative Management, 2009, 6(4): 353-369.

[17]Robinson T J, Pintar A L, Anderson-Cook C M, et al. A Bayesian approach to the analysis of split-plot combined and product arrays and optimization in robust parameter design[J]. Journal of Quality Technology, 2012, 44(4): 304-320.

[18]茆诗松, 王静龙, 濮晓龙. 高等数理统计[M]. 北京: 高等教育出版社, 2006.

Mao Shisong， Wang Jinglong， Pu Xiaolong. Advanced Mathematical Statistics[M]. Beijing: Higher Education Press, 2006. (in Chinese)

[19]Del Castillo E. Process Optimization: A Statistical Approach[M]. New York: Springer, 2007.

[20]Ortiz F, Simpson J R, Pignatiello J J, et al. A genetic algorithm approach to multiple-response optimization[J]. Journal of Quality Technology, 2004, 36(4): 432-450.

[21]Jourdan L, Basseur M, Talbi E-G. Hybridizing exact methods and metaheuristics: A taxonomy[J]. European Journal of Operational Research, 2009, 199(3): 620-629.

[22]何桢, 朱鹏飞. 基于模式搜索的渴求函数法在多响应优化中的应用[J]. 数学的实践与认识, 2009, 39(18): 114-121.

He Zhen, Zhu Pengfei. Application of pattern search algorithm to multiresponse optimization based on desirability functions[J]. Mathematics in Practice and Theory, 2009, 39(18): 114-121. (in Chinese)

[23]汪建均, 马义中. 基于GLM的双响应曲面法及其稳健设计[J]. 系统工程与电子技术, 2012, 34(11): 2306-2311.

Wang Jianjun, Ma Yizhong. Dual reponse surface methodology based on generalized linear models and its application on robust design[J]. Systems Engineering and Electronics, 2012, 34(11): 2306-2311. (in Chinese)

[24]Myers R H, Montgomery D C, Anderson-Cook C M. Response Surface Methodology: Process and Product Optimization Using Designed Experiments[M]. New York: John Wiley & Sons Inc, 2009.

[25]Frisbee S E, McGinity J W. Influence of nonionic surfactants on the physical and chemical properties of a biodegradable psuedolatex[J]. European Journal of Pharmaceutics and Biopharmaceutics, 1994, 40(6): 355-363.

[26]Ng S H. A Bayesian model-averaging approach for multiple-response optimization[J]. Journal of Quality Technology, 2010, 42(1): 52-68.

[27]汪建均, 马义中. 结合GLM与因子效应原则的贝叶斯变量选择方法[J]. 系统工程理论与实践, 2013, 33(8): 1975-1983.

Wang Jianjun, MaYizhong. Bayesian variable selection method combining generalized linear models with fractorial effect principles[J]. Systems Engineering-Theory & Practice, 2013, 33(8): 1975-1983. (in Chinese)

[28]Wang J J, Ma Y Z. Bayesian analysis of two-level fractional factorial experiments with non-normal responses[J]. Communications in Statistics-Simulation and Computation, 2013, 42(9): 1970-1988.

Bayesian modeling and optimization of multi-response robust parameter design

WANGJian-jun1, 2,MAYi-zhong1,OUYANGLin-han1,SUNJin-sheng2,LIUJian1

1.SchoolofEconomicsandManagement,NanjingUniversityofScienceandTechnology，Nanjing210094,China;2. School of Automation, Nanjing University of Science and Technology, Nanjing 210094, China

Abstract：A new optimization model, integrating quality loss function and posterior probability approach in the framework of Bayesian statistical modeling, is proposed to solve the problem of multi-response robust parameter design. The proposed method not only assesses the expected probability of each response which falls within its respective specification limit (i.e., the reliability of optimization results) using posterior probability approach, but also measures the robustness of multivariate process with quality loss function. In addition, this paper discusses,by illustrative examples,the relationship between joint posterior probability and marginal posterior probability,the influence of different expected probability on the optimization results of the proposed approach, and how to obtain the optimum balance between quality loss and posterior probability. The results show that the proposed method can simultaneously take into consideration the robustness of multivariate process and the reliability of optimization results, and provide a relatively satisfactory optimization result from several respects (e.g., robustness of multivariate process, the reliability of optimization results) to achieve robust parameter design with multiple responses.

Key words:Bayesian analysis; multiple responses; posterior probability; quality loss function; robust parameter design

中图分类号:F273.2

文献标识码:A

文章编号:1007-9807(2016)02-0085-10

作者简介:汪建均(1977—)， 男， 湖南慈利人， 博士， 副教授， 硕士生导师. Email: jjwang@njust.edu.cn

基金项目：国家自然科学基金资助项目(71371099； 71301075； 71471088)； 中国博士后科学基金第七批特别资助项目(2014T70527)； 中国博士后基金资助项目(2013M531366)； 教育部高等学校博士学科点专项科研基金资助项目(20123219120032)； 中央高校基本科研业务专项资金资助项目(3091511102).

收稿日期：① 2013-08-05；

修订日期：2014-08-19.