面向多重不确定性的发电商碳减排投资研究①

王素凤， 杨善林， 彭张林

(1. 安徽建筑大学管理学院， 合肥 230601； 2. 合肥工业大学管理学院， 合肥 230009)



面向多重不确定性的发电商碳减排投资研究①

王素凤1， 杨善林2， 彭张林2

(1. 安徽建筑大学管理学院， 合肥 230601； 2. 合肥工业大学管理学院， 合肥 230009)

摘要：基于技术进步、电力价格、燃料价格、碳价、补贴政策和投资项目的碳减排率等多重不确定因素，构建了发电商减排投资的实物期权模型，求解得到了投资阈值、投资时点和投资补贴条件.参数敏感性分析和仿真结果表明：碳价波动风险抑制了减排投资；技术进步和投资补贴能够激励发电商投资，但当前的碳价和技术水平无法支撑CCS项目的大规模应用；合作减排有利于发现碳减排率较高的项目，进而刺激发电商的投资行为.

关键词：多重不确定性； 碳减排； 投资； 实物期权； 发电商

0引言

全球气候的日益变暖和极端灾害事件的频繁发生，使得以二氧化碳(carbon dioxide，CO2)为主的温室气体(green house gas，GHG)减排形势日益严峻.作为发展中国家，中国目前并不承担国际强制的碳减排义务，但考虑到庞大的碳排放总量和未来排放增长需求、经济社会可持续发展以及国际社会施加的政治压力，中国政府承诺至2020年，单位国内生产总值碳排放在2005年基础上削减40%-45%.据统计，2010年发电导致的碳排放接近于全国碳排放总量的41%[1].因此，要实现上述减排目标，电力行业首当其冲.电厂碳减排主要有两条途径：一是从外部市场购买排放权，二是自主减排.由于当前国内碳市场尚处在试点阶段、碳交易稀疏，依靠外部买入的减排方式缺乏保障，只有通过自主减排降低碳排放更具现实意义和可持续性.自主减排又可以进一步分为4类：优化能源结构(即选择更为低碳的能源作为燃料，例如提高天然气在发电能耗中所占的比例)、提高能源效率、实施碳捕集与封存(carbon capture and storage，CCS)以及可再生能源发电(renewable energy generation，REG)(包括但不限于水电、风电、光伏发电、生物质发电、核电).

考虑到中国以煤为主的能源资源构成在短期内不会改变，通过调整能耗结构减排的潜力不大.同时，在当前的技术水平下提高能效产生的减排量亦很有限.而可再生能源项目(renewable energy project，REP)的减排成本又很高昂[2-3]，因此，就减排潜力和经济性而言，CCS的优势最为显著，可为实现全球碳减排目标贡献20%以上[4].但CCS投资受电价、碳价、燃料价格、补贴政策等外部因素和技术进步、减排率等内部因素的影响，存在高度的不确定性；同时，较高的投资成本和投资风险也常迫使发电商延迟甚至放弃投资，不利于排放企业以成本有效的方式完成减排目标，也不利于环境、经济和社会的可持续发展.目前，针对CCS减排投资的研究已经涌现了许多成果[5].其中比较传统的评估方法是贴现现金流(discount cash flow，DCF)法，但DCF法不能充分量化分析项目投资的风险和不确定性，从而不利于碳减排投资决策的实施与优化.研究不确定环境下最优投资的有效工具是实物期权(real options，RO)理论[6-7].Myers和Turnbull[8]、Ross[9]最早提出了实物期权定价方法；McDonald和Siegel[10]首次构建了RO评估模型，并利用期权定价法求解；Brennan和Schwartz[11]则将RO法引入到自然资源投资决策中.此后，RO方法开始在能源和技术投资评估中得到广泛应用[12-17].

Fleten和Näsäkkälä[18]考虑电价和天然气价格的不确定性，利用RO法分析天然气发电项目放弃期权的价值.在此基础上，Zhou等[19]将碳价不确定性纳入RO模型，分析中国电力行业的CCS投资策略.Oda和Akimoto[20]运用RO法研究了“等待”和“立即投资”之间的分界值，指出在不确定条件下，CCS技术扩散需要较高的碳价(约为US$70/tCO2)支撑；而当前主流的碳排放权免费分配方式使得CCS投资很难实施.Cheng等[21]提出了改进的二项顺序复合期权模型，可扩展用于求解一般的决策问题.Lin和Huang[22]成功地将传统托宾Q与RO的评估准则相结合，针对那些尚未安装节能设施的企业，探寻实施或退出节能投资项目的最佳时机.但他们的模型只考虑了成本与收益的不确定性，未虑及其它不确定因素.Zhu和Fan[23]发现，当前的CCS投资风险过高，气候政策对CCS发展有极大影响，决策者需要在减少GHG排放和保护电力企业利益之间进行权衡.Heydari等[24]基于电力、CO2、煤炭价格的不确定性，建立了RO模型，对煤电厂实施全局CCS和局部CCS两类减排技术予以评估，认为最优停止边界条件对CO2价格波动高度敏感.Zhu和Fan[25]依据RO理论，构建了离散序列投资决策评估模型，分析现有超临界煤粉(supercritical pulverized coal，SCPC)CCS技术改造的投资决策，指出营运与维护(O&M)成本是影响CCS改造投资的最重要因素；当前的CCS技术水平和政策框架无法支撑电力厂商对SCPC的CCS改造.Cristóbal等[26]在总量控制与交易框架下，提出了两阶段随机混合整数线性规划(mixed-integer linear programming，MILP)方法，研究碳许可价格不确定条件下CCS项目的最佳投资时机和运营策略.

上述研究主要考虑的是电价、碳价和能源价格等外生不确定因素对减排投资决策的影响，针对技术进步等内生不确定性的分析不够深入.此外，由于成本过高，减排投资常被延迟甚至放弃[27-28]，因此有必要分析项目减排率对投资决策的影响，但这方面的研究十分匮乏.进一步地，为了增加投资机会、降低投资风险，还可以考虑一个减排项目由多家企业合作或一个企业参与多个项目的情形，这类似于《京都议定书》所提出的清洁发展机制(clean development mechanism，CDM)和联合履约(joint implementation，JI).Vithayasrichareon和MacGill[29]提出了不确定环境下的发电组合决策支持工具，以一个煤电厂、联合循环燃气轮机(combined cycle gas turbine，CCGT)和开式循环燃气轮机(open cycle gas turbine，OCGT)为例，研究了电价、碳价和燃料价格不确定性对发电决策的影响.该工具可支持复杂的投资组合风险评估，但模型主要针对新建电厂的投资进行分析，未考虑对现有电厂的改造；同时，模型重点讨论煤电和气电技术投资，关于其它非化石能源发电技术的投资决策有待于进一步展开研究；并且模型研究的是发电投资，而非碳减排项目的投资问题.

与以往研究相比，本文综合考虑了技术进步、项目(技术)减排率、电价、碳价和补贴政策等内、外部不确定因素的变化，构建了碳减排投资RO模型，求解得到投资阈值、投资时点(期望首达时间)以及减排投资补贴的解析条件；在此基础上，对相关参数展开敏感性分析，并借助蒙特卡罗(Monte Carlo)方法模拟减排投资的期权价值分布规律，考察不确定因素对投资阈值和投资时点的影响，以期为政府制订碳排放政策和企业减排投资决策提供参考依据.

1碳减排投资模型

某发电商拟通过减排投资降低碳排放，需要确定是否投资、何时投资以及投资于何项目等问题.此时，发电商面临市场电价、燃料价格和碳价等外部不确定性.Dixit和Pindyck[30]分析了电价和燃料价格的变化规律，指出可用几何布朗运动(geometric Brownian motion，GBM)对其加以描述.此外，有关国际上最成熟的碳市场——欧盟碳交易市场——的实证研究[31-32]也表明，碳价波动服从类似的过程.国内碳市场尚未形成，仅深圳等少数地区于2013年启动了碳交易试点，由于其发展历程较短，目前不具备中长期碳价变化实证分析的条件，故此处假设国内发电商CCS投资所面临的碳价也遵循几何布朗运动.于是有

(1)

式中Pt、Ft、Ct分别表示电价、燃料价格(表征发电成本)和碳价(表征排放成本)；μi、σi、dWi(i=P,F,C)为相应项的漂移率、波动率和标准维纳过程；t=1,2,…代表时间.设价格变量之间的相关系数为零.做出这种假设的合理性在于，在3种外生性的价格因素中，本文着重讨论碳价波动对减排投资决策的影响，而一般地，碳价作为碳排放成本的衡量指标，其与电力价格和燃料价格之间没有明显的相关关系，或者说忽略这种相关性不会对研究结论产生显著影响.另外，为了更清晰地展现投资决策对碳价变化的敏感性，在不改变最终结论的前提下，可先假定短期内电价、燃料价格不发生显著变化，故这二者之间的相关性也可不予考虑.

此外，技术创新将引发技术变迁，这种不确定的技术进步会影响CCS的成本，包括投资成本It(投资可能是一次性的，也可能分阶段进行，本文考虑前一种情况)和日常运行维护成本Mt(主要指碳捕获/运输/封存、设备故障、维修成本等，以下简称运行成本).随着技术的进步，这两类成本均会下降.参照Fuss和Szolgayová[33]，假定单位减排投资成本It及运行成本Mt满足

(2)

式中随机变量H(t)>0服从参数为λ的泊松分布；0≤ξi≤1(i=1,2)反映技术进步对投资成本或运行成本的影响，为简化分析，不妨设ξ1=ξ2=ξ.λt表示技术进步的次数，因此，It的期望为I0e-λt(1-ξ).类似地，Mt的期望为M0e-λt(1-ξ).当λ(1-ξ)为常量时，技术进步的期望路径保持不变.

对该发电商而言，单位发电量碳减排投资的价值函数V为

(3)

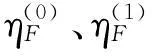
(4)

上式的贝尔曼方程(Bellman equation)为

rVdt=E(dV)

(5)

式中E(·)表示期望.投资价值V的变动dV由4部分构成：1)电价Pt波动引起的价值变化；2)发电成本Ft的波动引起的价值变化；3)碳排放成本Ct的波动引起的价值变化；4)H(t)的波动引起运行成本Mt和投资成本It的变化，进而导致价值变化.前3种变化均为连续性的，第4种则为跳跃性的泊松过程.

如前所述，为重点考察技术进步和碳价等变量对减排投资决策的影响，这里先将Pt和Ft视为常量.由伊藤引理(Ito’s lemma)对式(5)右端进行展开可得

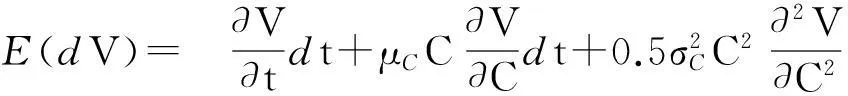
λ[V(C,ξI)-V(C,I)]dt

(6)

将式(6)代入式(5)，整理得

(r+λ)V(C,I)+λV(C,ξI)=0

(7)

式(7)是个不规范的偏微分方程，其解的一般形式为

(8)

式中A为待定系数；Z为积分常数；β为式(7)所对应的特征方程的根,β>1.

根据价值匹配(value matching)与光滑粘贴(smooth pasting)条件，有

(9)

由式(8)和式(9)，不难得到

(10)

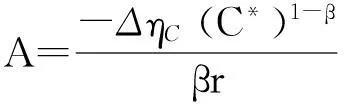
C*即为减排投资的阈值，仅当碳价C≥C*时，发电商的最优选择才是“投资”；否则，发电商将选择“延迟”或“放弃”.

对于现有火电厂的减排投资改造，一般有ΔηF>0(反映了热效率的下降)，但同时有ΔηC<0(反映了碳排放率的减小或减排率的增大)，体现了减排投资的价值.由式(10)易知，投资阈值C*随ΔηF、|ΔηC|分别呈递增和递减的关系.另外，C*随补贴比例θ的增大而减小，表明补贴越多，投资门槛就越低，对减排投资的激励作用越显著.

再由Murto[34]，有

(11)

在临界值C*处，企业的减排投资行为相当于一次技术升级.经过简单变换，易得减排技术投资的期望投资时点(以首达时间表示)为

(12)

在期望投资时点，结合式(10)、式(12)，可进一步求得最佳投资补贴比例

(13)

2数值分析

根据式(10)和式(12)，若视ΔηF为常量，则参数β,r,θ,I,ΔηC,M均会对C*、ET*产生影响.再结合式(2)和式(11)可知，投资阈值C*和期望首达时间由参数μC,σC,r,θ,ξ,λ，ΔηC共同决定.现以某火力发电厂为例，该电厂装机容量600 MW(这是目前国内电网中的主流机组)，负荷因子80%.根据有关文献[2,28,35-37]，经数据整理和合理假设，获得投资模型的已知参数(见表1).

表1中关键参数设置的依据如下：

表1　模型参数设置

2)当前碳价C0的取值参考了深圳碳市场的价格水平.自深圳启动碳交易以来，市场平均成交价已超过70元/tCO2，且预计未来仍有较大的上涨空间，此处假设碳价为80元/tCO2；

3)发电厂的燃料成本F以电厂消耗的煤炭价格表征，结合国内实际，设该值为500元/tce，“tce”表示吨标煤(tonne coal equivalent)；

4)Q为年发电量，是装机容量与年利用小时(设为6 500 h)的乘积，即年发电量Q为600 MW×6 500 h=3.9×106MWh；

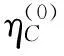
7)CCS初始投资成本与燃煤电厂规模、预计年碳捕集量等因素有密切关系，借鉴文献[28]和[37]，假设CCS投资需新增成本10.5亿元，则I0为1 050/3.9≈269，不妨取整为270(元/MWh)；

8)关于初始运行成本M0的估算，参考文献[2]，设CCS设施的碳减排成本为450 元/tCO2；同时结合第6)条，取CCS改造后的碳排放率为0.15(tCO2/MWh)，则M0为450×0.15=67.5(元/MWh).

为考察上述不确定因素对碳减排投资决策的影响，2.1节至2.3节将利用Matlab 2010b仿真软件，绘制相关参数的敏感性分析图，分别探讨投资阈值和期望投资时点随各项参数变化的情形，并讨论在不同的技术进步率下政府的最佳补贴政策.

2.1碳价波动与减排投资决策

2.1.1碳价波动对投资阈值的影响

基于表1的参数条件，图1给出了不同碳价波动率和投资成本下的投资阈值.

图1　投资阈值C*随参数σC,I的变化曲线

图1显示：第1，投资阈值C*与碳价波动率σC呈同方向变化.以投资成本I=270元/MWh为例，当σC从0.01增至0.05时，投资阈值也由369元/tCO2提高到了378元/tCO2，表明随着碳价波动风险不断加大，需要更高的碳价才能触发减排投资，这一结论与文献[27]一致.第2，投资阈值C*随投资成本I的下降而减小.例如当σC=0.05时，随着投资成本从370元/MWh降至270元/MWh，投资阈值也由390元/tCO2减至378元/tCO2.这意味着投资成本的降低有诱导发电商进行减排投资的效果.降低投资成本主要有两条途径：一是通过技术进步提高投资回报率，从而减少投资成本；二是对投资活动提供税收抵免或补贴.后文将对此展开具体分析.

2.1.2碳价波动对投资时点的影响

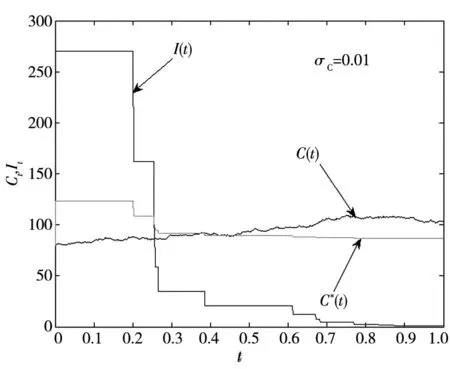
的运行轨迹

由于投资时点的不确定性，本文以期望首达时间ET*作为考察对象，研究相关参数对投资时点的影响.注意到，碳价的波动风险不仅影响投资价值的大小，也影响投资时点的早晚.在不同的碳价波动率σC下，得到期望首达时间ET*的变化曲线如图3所示(除σC以外，其它参数与图2一致)；再运用蒙特卡罗模拟方法，对投资价值V进行50 000次仿真，得到图3中的投资价值直方图(纵坐标N代表仿真次数).

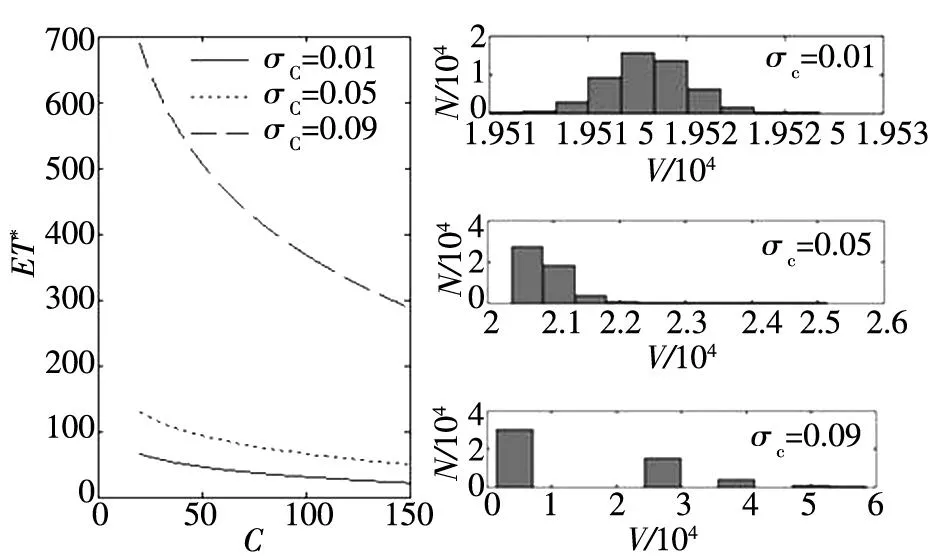
图3　参数σC对ET*和投资价值V的影响

由图3可知：第1，当碳排放价格的不确定性较小(σC=0.01)时，投资价值虽然较低但分布较为稳定(基本位于19.52×103附近)；并且，相对而言，碳价波动风险越小，投资时点到来的也越早，不过在当前的碳价水平(C0=80)下，投资时机至少需要二十几年的时间才能出现，因此当前发电商的最优选择是“延迟投资”.第2，随着参数σC的增大，期望首达时间ET*和投资价值V都将上升，但投资价值的稳定性明显下降.第3，当σC→0.1时，投资价值的波动最大、风险最高，多数情况下的投资价值接近或等于零，此时发电商将选择“放弃”投资.由此可得如下结论：碳价不确定性使减排投资延迟、投资风险增大，极端情况下发电商将放弃投资.需要说明的是，由于参数设置不同，图3中的模拟结果与文献[27]略有差异，但所得结论基本一致.

2.2技术进步、补贴比例与减排投资决策

一方面，技术创新通过作用于CCS投资成本和运行成本，改变着投资阈值与投资时机；另一方面，补贴比例也会影响投资决策，而技术进步则进一步强化了投资补贴的政策效应，对减排投资决策产生重要影响.

2.2.1技术进步对投资阈值的影响

为深入考察不同技术进步率下投资阈值的变化，分别令λ=0.5和ξ=0.6，图4(a)、(b)分别给出了投资阈值C*随参数ξ,λ变化的曲线关系.

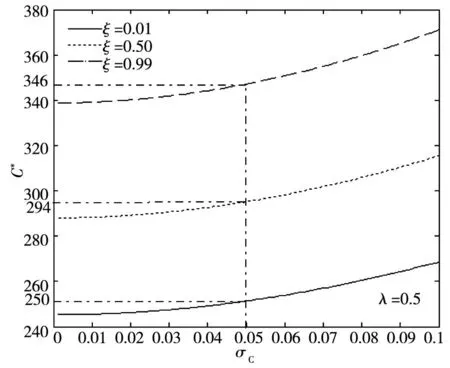
(a) 投资阈值C*随参数ξ的变化曲线

(b) 投资阈值C*随参数λ的变化曲线

由图4可以直观地发现：首先，在图(a)中，投资阈值C*随ξ的增大而增大(如在σC=0.05处，C*由250增至294、346).ξ越大，技术进步对投资成本和运行成本的影响就越小，当ξ→1时，技术进步对投资阈值基本没有影响；而当ξ→0时，技术进步对投资阈值的影响达到最大.其次，在图(b)中，投资阈值C*随λ的增大而减小(如C*由340降至303、274)，表明随着技术进步的概率增大，投资成本和运行成本不断下降，只需相对较低的碳价便可诱发投资.

类似地，随着技术的不断进步，投资的门槛降低，期望首达时间也将提前来临.反之则相反.具体分析不再赘述.

2.2.2补贴比例对投资阈值的影响

令ξ=0.6、λ=0.01，图5刻画了补贴比例θ的不确定性对投资策略的影响(其余参数见表1).

根据式(10)，再分析图5可知，提高投资补贴比例，可降低投资成本，进而使投资阈值下降(如在σC=0.05处，θ的增大使C*由374依次降至347、320).换言之，投资补贴具有刺激减排投资的效应.这一结论与文献[28]一致.事实上，除了直接补贴外，投资税收抵免、对技术创新提供碳排放权奖励等措施，均具有类似的激励作用.

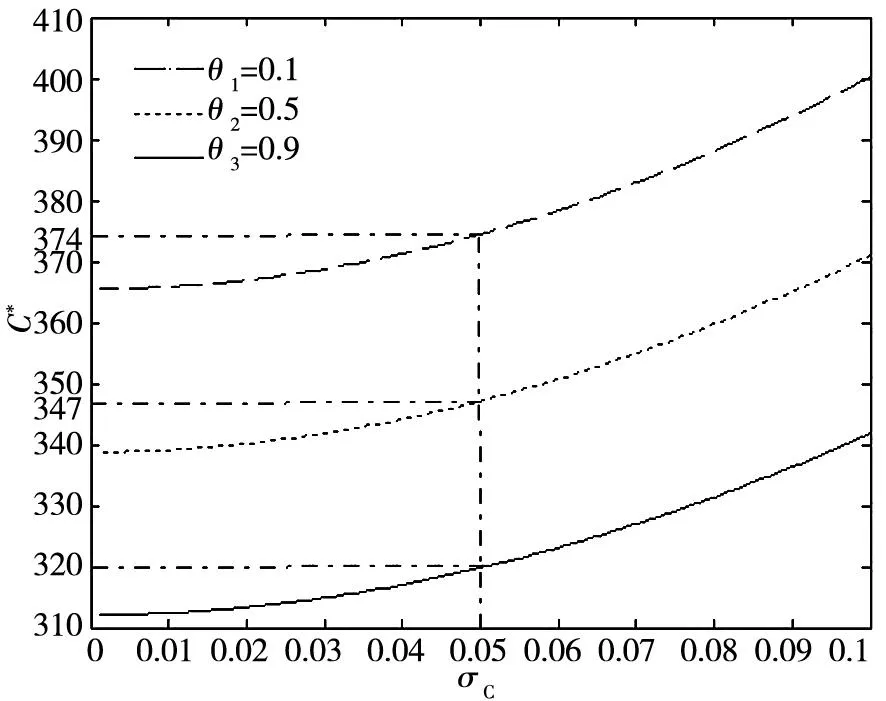
图5　投资阈值C*随参数θ的变化曲线

2.2.3不同技术进步率下补贴政策的效果

此处主要以参数λ表征技术进步的不确定性.根据式(12)、(13)，假定σC=0.01，ξ=0.6，并分λ=0.1、λ=0.5和λ=0.9三种情形，利用图6描述不同补贴水平下投资时点的变化情况(为便于比较和阅读，将三组结果分别列示于40～90、90～180、180～271三个不同的碳价区间).

从图6中可以得出两点结论：首先，在当前的碳价水平(C0=80)下，无论补贴比例有多高，在3组技术进步率下，投资时点的来临平均都需要25年以上；若λ=0.1，则无论补贴比例如何变化，首达时间都将长达32年至37年.换句话说，较低的碳价阻碍了“碳排放权”这一环境资源稀缺性的凸显，现阶段仅靠投资补贴对CCS投资所能产生的激励作用十分微弱.其次，随着碳价逐渐上升，技术进步率越大，补贴政策对减排投资的促进效果就越明显.当碳价高达271元/t时，在λ=0.9的技术进步水平下，若给予10%的投资补贴，则期望首达时间可缩短至4年；若补贴比例增加至90%，发电商将选择立即投资CCS技术.同样地，由于研究期间及研究对象的不同，此处的分析结果与文献[28]在数值上存在一定差异，但基本结论仍是相符的，即都认为CCS的大规模商业化运作尚需较长时日.

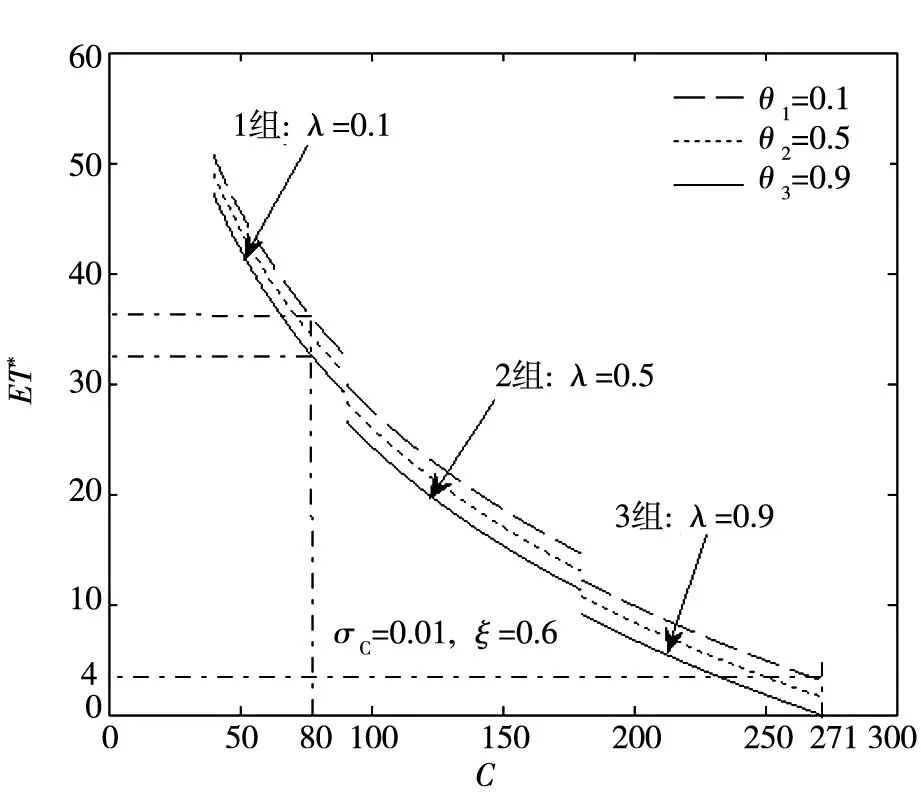
图6　不同技术进步率下补贴政策的效应

可见，最佳补贴比例θ的确定与技术进步率λ和碳价水平C0密切相关.特别地，当碳价较高(≥271元/tCO2)时，补贴政策的效果将主要取决于技术进步率的高低.

2.3碳排放率变化与减排投资决策

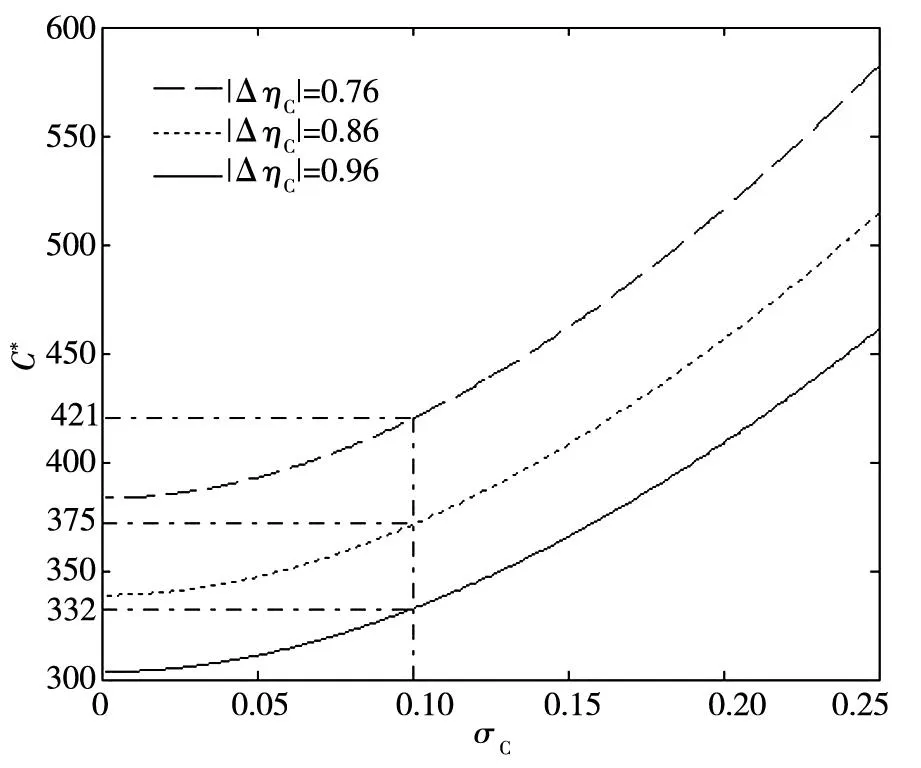
图7　投资阈值C*随参数|ΔηC|的变化曲线

需要注意的是，上述分析中假定电力价格和燃料成本短期内不发生明显变化.一旦放开这一假设，还要考虑电力价格、燃料成本等因素的变化对CCS减排投资决策造成的影响.此时，投资决策条件(式(10)和式(12))以及补贴比例条件(式(13))都将发生改变，但具体的分析方法是类似的，限于篇幅，不再展开.

3结束语

本文假定电价、燃料价格和碳价服从几何布朗运动，技术进步遵循泊松跳跃过程，建立了发电商减排投资(包括但不限于CCS)实物期权模型，求解得到了投资阈值条件、投资时点(期望首达时间)和最佳投资补贴规则.借助参数敏感性分析，考察减排投资决策随碳价波动、技术进步、补贴比例、项目(技术)减排率等不确定因素变化而变化的规律；并运用蒙特卡罗方法模拟了投资价值分布直方图，分析碳价风险与投资时机、投资价值的关系，结果表明：

第1，随着碳价波动幅度增大，投资风险增加，导致投资阈值上升、投资时点延迟，当风险达到一定水平，发电商将放弃投资.典型的例子如欧盟排放贸易体系(EU ETS)，2005年—2008年间该市场的碳价震荡剧烈，最高时超过30欧元，最低时不足1欧元，巨大的市场风险使得企业的减排投资动力几近丧失.为避免出现类似现象，我国政府需要加快出台相关政策，促进碳市场发展、明晰政策信号、抑制碳价过快过大波动，帮助发电商形成稳定的市场预期.在当前的碳交易试点阶段，可允许碳配额跨期存储与借贷以平滑各期碳价波动；另外，对企业自主减排所创造的减排量进行认定，如予以相应奖励，或在未来的强制减排阶段按照一定比例折算成碳信用以抵销企业的减排义务，这样既可实现碳价由自愿减排期向强制减排期的平稳过渡，又赋予了企业获取减排投资收益和碳信用抵免的双重好处，可有效发挥碳市场在引导企业自主减排投资上的作用；

第2，技术进步和投资补贴均可降低投资成本，具有刺激发电商投资于减排技术的作用，但这种效果还需要高碳价的配合，当碳价达到或超过一定水平(本文研究为271元/tCO2)时，技术进步率与投资补贴对减排投资的激励效应最为显著.目前的碳价和技术水平尚无法支撑CCS投资的大规模应用.针对这种情况，建议相关部门加大CCS等减排技术的研发投入和奖励力度，鼓励清洁能源发电技术的创新与推广，降低发电商碳减排的投资成本.同时，配合投资税负优惠或抵免、清洁能源发电投资补贴等举措，提高发电商减排投资的积极性.此外，随着国际气候减排形势日益严峻和国内节能减排工作的快速推进，碳配额作为环境资源，其价值性和稀缺性将逐步显现，碳价趋于升高，政府也应适时引导电力企业做好能源结构转型、发电及减排技术升级的准备，把握CCS等减排技术的投资契机，积极参与碳交易；

第3，项目(技术)减排率的大小对投资阈值和投资时点有重要影响.以现有电厂减排改造为例，预期改造后的减排率越高，越能诱导发电商的投资行为.在一定的碳捕集技术水平下，减排投资的回报率主要受方案甄选成本和减排量交易成本的影响.因此，一方面，政府可通过官方网站或权威机构发布减排项目信息，提高发电商减排项目(技术)选择的灵活性，降低投资方案的遴选成本；另一方面，还要推动并规范碳市场建设，增大价格透明性，减小交易成本，从而提高减排项目的投资回报率.进一步地，考虑到当前CCS投资的高昂成本和不确定性风险，可由政府出面整合小型火电厂，提高发电商的投资能力和风险抵御能力；也可借鉴国际碳市场上CDM或JI的减排合作模式，由几家发电厂共同出资实施CCS项目，利用联合投资来降低发电商的资金压力并分散投资风险，各电厂根据投资比例分享项目所创造的减排收益.

相较于同类研究，本文构建的模型系统分析了存在内、外部多重不确定因素的条件下，发电商碳减排投资决策的变化；模型不仅适用于发电商的减排投资分析，也可用于对不同的减排项目(技术)优选排序；若将模型中的电力价格视为一般商品的市场售价、将燃料价格看作企业生产的要素投入成本，则模型还可拓展用于非电力企业的减排投资研究，这体现了模型的一般性.

鉴于现实中发电商碳减排投资决策所面临的不确定因素可能更为复杂且相互交织，未来研究有必要将电力市场的竞争结构和减排创造的碳信用纳入模型，并考虑电力市场与碳市场的交叉作用.进一步地，许多减排投资并非一次完成而是分阶段进行的，在初始投资之前或在项目设计时就考虑后续投资的期权价值将更具有现实意义.

参 考 文 献:

[1]IEA. CO2Emissions from Fuel Combustion 2012 Edition[R]. Paris: OECD/IEA, 2012.

[2]徐钢， 田龙虎， 刘彤， 等. 中国电力工业CO2减排战略分析[J]. 中国电机工程学报， 2011， 31(17)： 1-8.

Xu Gang, Tian Longhu, Liu Tong, et al. Strategic analysis of CO2mitigation in Chinese power industy[J]. Proceedings of the CSEE, 2011, 31(17): 1-8. (in Chinese)

[3]Zhu L. A simulation based real options approach for the investment evaluation of nuclear power[J]. Computer & Industrial Engineering, 2012, 63(3): 585-593.

[4]IEA. World Energy Outlook 2011[R]. Paris: OECD/IEA, 2011.

[5]梁大鹏， 徐春林， 马东海. 基于系统动力学的CCS产业化模型及稳态研究[J]. 管理科学学报， 2012， 15(7)： 36-49.

Liang Dapeng, Xu Chunlin, Ma Donghai. The research on the model and stability of CCS based on the system dynamics[J]. Journal of Management Sciences in China, 2012, 15(7): 36-49. (in Chinese)

[6]Yang M, Blyth W. Modeling Investment Risks and Uncertainties with Real Options Approach[R]. Paris: LTO/2007/WP 01, IEA , 2007.

[7]何沐文， 刘金兰， 高奇特. 不确定环境下自然资源开发项目投资评价模型[J]. 管理科学学报， 2013， 16(6)： 46-55.

He Muwen, Liu Jinlan, Gao Qite. An investment evaluation model for natural resource development project under multiple uncertainties[J]. Journal of Management Sciences in China, 2013, 16(6): 46-55. (in Chinese)

[8]Myers S C, Turnbull S M. Capital budgeting and the capital asset pricing model: Good news and bad news[J]. The Journal of Finance, 1977, 32(2): 321-333.

[9]Ross S. A simple approach to the valuation of risky streams[J]. The Journal of Business, 1978, 51 (3): 453-475.

[10]McDonald R, Siegel D. Thevalue of waiting to invest[J]. The Quarterly Journal of Economics, 1986, 101(4): 707-728.

[11]Brennan M J, Schwartz E S. Evaluating natural resource investments[J]. The Journal of Business, 1985, 58(2): 135-157.

[12]Paddock J L, Siegel D R, Smith J L. Option valuation of claims on real assets: The case of offshore petroleum leases[J]. The Quarterly Journal of Economics, 1988, 103(3): 479-508.

[13]Smith J E, Nau R F. Valuing risky projects: Option pricing theory and decision analysis[J]. Management Science, 1995, 41(5): 795-816.

[14]安瑛晖， 张维. 期权博弈理论的方法模型分析与发展[J]. 管理科学学报， 2001， 4(1)： 38-44.

An Yinghui, Zhang Wei. Analysis and development of the method and model of option-game theory[J]. Journal of Management Sciences in China, 2001, 4(1): 38-44. (in Chinese)

[15]陈黎明， 邱菀华. 不确定环境下新技术投资策略模型研究[J]. 管理科学学报， 2005， 8(4)： 9-14， 27.

Chen Liming, Qiu Wanhua. Study on investment strategy model of technological innovations under uncertainty[J]. Journal of Management Sciences in China, 2005, 8(4): 9-14, 27. (in Chinese)

[16]Fan Y, Zhou L. A real options based study on overseas oil investment and its application in China’s oversea oil investment[J]. Energy Economics, 2010, 32: 627-637.

[17]张新华， 叶泽， 赖明勇， 等. 考虑价格上限的寡头发电投资阈值与容量选择[J]. 管理科学学报， 2012， 15(9)： 1-9.

Zhang Xinhua, Ye Ze, Lai Mingyong, et al. Investment threshold and capacity choice with price cap in oligopoly electric power market[J]. Journal of Management Sciences in China, 2012, 15(9): 1-9. (in Chinese)

[18]Fleten S E, Näsäkkälä E. Gas-fired power plants: Investment timing, operating flexibility and CO2capture[J]. Energy Economics, 2010, 32(4): 805-816.

[19]Zhou W, Zhu B, Fuss S, et al. Uncertainty modeling of CCS investment strategy in China’s power sector[J]. Applied Energy, 2010, 87: 2392-2400.

[20]Oda J, Akimoto K. Ananalysis of CCS investment under uncertainty[J]. Energy Procedia, 2011, 4: 1997-2004.

[21]Cheng C T, Lo S L, Lin T T. Applying real options analysis to assess cleaner energy development strategies[J]. Energy Policy, 2011, 39(10): 5929-5938.

[22]Lin T T, Huang S L. Application of the modified Tobin’s q to an uncertain energy-saving project with the real options concept[J]. Energy Policy, 2011, 39(1): 408-420.

[23]Zhu L, Fan Y. A real options-based CCS investment evaluation model: Case study of China’s power generation sector[J]. Applied Energy, 2011, 88(12): 4320-4333.

[24]Heydari S, Ovenden N, Siddiqui A. Real options analysis of investment in carbon capture and sequestration technology[J]. Computational Management Science, 2012, 9(1):109 -138.

[25]Zhu L, Fan Y. Modelling the investment in carbon capture retrofits of pulverized coalfired plants[J]. Energy, 2013, 57(C): 66-75.

[26]Cristóbal J, Guillén-Gosálbez G, Kraslawski A, et al. Stochastic MILP model for optimal timing of investments in CO2capture technologies under uncertainty in prices[J]. Energy, 2013, 54: 343-351.

[27]张新华， 叶泽， 李薇. 价格与技术不确定条件下的发电商碳捕获投资模型及分析[J]. 管理工程学报， 2012， 26(3)： 109-113.

Zhang Xinhua, Ye Ze, Li Wei. The power producer’s carbon capture investment model and its analysis under price and technology uncertainties[J]. Journal of Industrial Engineering, 2012, 26(3): 109-113. (in Chinese)

[28]陈涛， 邵云飞， 唐小我. 多重不确定条件下发电与CCS技术的两阶段投资决策分析[J]. 系统工程， 2012， 30(3)： 37-44.

Chen Tao, Shao Yunfei, Tang Xiaowo. Coal-fired power and CCS investment decision-making issue based on a two stage investment model under multiple uncertain conditions[J]. System Engineering, 2012, 30(3): 37-44. (in Chinese)

[29]Vithayasrichareon P, MacGill I F. A Monte Carlo based decision-support tool for assessing generation portfolios in future carbon constrained electricity industries[J]. Energy Policy, 2012, 41: 374-392.

[30]Dixit A K, Pindyck R S. Investment under Uncertainty[M]. NJ: Princeton University Press, 1994.

[31]Luis M A, José M C. European CO2prices and carbon capture investments[J]. Energy Economics, 2008, 30(6): 2992-3015.

[32]凤振华. 碳市场复杂系统价格波动机制与风险管理研究[D]. 合肥： 中国科学技术大学， 2012.

Feng Zhenhua. Price volatility and risk management models for carbon market complex system[D]. Hefei: University of Science and Technology of China, 2012. (in Chinese)

[33]Fuss S, Szolgayová J. Fuel price and technological uncertainty in a real options model for electricity planning[J]. Applied Energy, 2010, 87(9): 2938-2944.

[34]Murto P. Timing of investment under technological and revenue-related uncertainties[J]. Journal of Economics Dynamics & Control, 2007, 31(5): 1473-1497.

[35]Fuss S, Szolgayova J, Obersteiner M, et al. Investment under market and climate policy uncertainty[J]. Applied Energy, 2008, 85(8): 708-721.

[36]李星朗. 基于全寿命周期成本和价值工程的火电厂碳捕集改造研究[D]. 长沙： 长沙理工大学， 2012.

Li Xinglang. Based on the Life Cycle Cost Theory and Value Engineering of Coal-fired Power Plant’s Carbon Capture and Sequestration Technology Reform Investment Research[D]. Changsha: Changsha University of Science & Technology, 2012. (in Chinese)

[37]IEA. Coal in the Energy Supply of China[R]. Paris: OECD/IEA, 2012.

Research on the power producer’s carbon abatement investment in view of multiple uncertainties

WANGSu-feng1,YANGShan-lin2,PENGZhang-lin2

1. School of Management, Anhui Jianzhu University, Hefei 230601, China;2. School of Management, Hefei University of Technology, Hefei 230009, China

Abstract:After taking into account such uncertain factors as technological advance, electricity price, fuel price, carbon price, investment subsidy policies and emission reduction rate, we have constructed a real-option model for power producers’ carbon abatement. Based on this model, conditions of thresholds, timing and subsidy rules for abatement investment are presented. The results indicate that: (1) the risk of carbon price fluctuation inhibits investment in mitigation projects; (2) technological progress and investment subsidies will encourage investment in abatement projects, but current carbon price and technologies cannot support grand-scaled CCS investment; and (3) collaborative abatement projects may improve emission reduction rate, and thus stimulate power producers’ investments.

Key words:multiple uncertainties; carbon abatement; investment; real options; power producer

中图分类号:F830.59

文献标识码:A

文章编号:1007-9807(2016)02-0031-11

作者简介:王素凤(1978—)， 女， 安徽固镇人， 博士， 副教授， 硕士生导师. Email: wangsufeng927@ahjzu.edu.cn

基金项目：国家社会科学基金资助项目(12CJY033)； 教育部人文社科研究规划基金资助项目(15YJA790060)；安徽省软科学研究计划资助项目(1502052030)； 安徽建筑大学博士科研启动基金资助项目(2014-2-7).

收稿日期：① 2013-05-31；

修订日期：2014-03-24.