Banach空间上分数阶积分微分方程的可解性与可控性

高媛

（兰州交通大学数理学院，甘肃　兰州　730070）



Banach空间上分数阶积分微分方程的可解性与可控性

高媛

（兰州交通大学数理学院，甘肃兰州730070）

摘要：研究了Banach空间上一类具有非局部初始条件的分数阶积分微分方程的可解性与可控性。借助合适的不动点定理，本论述建立了适度解的存在性和可控性条件，变换非局部柯西问题（1）为等效的积分方程，并且通过使用阿尔泽拉-阿斯科利定理和Krasnoselskii不动点定理获得积分微分方程（1）的适度解。同时构建合适的控制函数，讨论了满足非局部初始条件的一类抽象积分微分发展方程（2）的可控性，最后举例论证了定理2.1的一个简单应用。

关键词：非局部条件；积分微分方程；适度解；可控性

DOI10.3969/j.issn.1672-6375.2016.02.022

0　引言

早在1993年，Miller和Ross就提出了分数阶的积分和微分[1]。之后，Podlubny又对分数阶微分方程做了详尽介绍[2]。此外，分数阶微分方程的相关发展也包括：文献[3]研究了二阶中立性积分微分方程解的存在性，[4]则研究了脉冲微分方程与积分微分方程解的存在性,在此基础上，[5]研究了脉冲偏微分方程适度解的存在性。但是在实际的问题和数学模型中，受局部条件和非局部条件的限制，文献[6]的主要结论是不能被应用的。本论述第三部分在文献[12]的基础上，讨论了形式如

满足非局部初始条件[8]的一类抽象分数阶积分微分方程的可解性，其中是阶Caputo分数阶导数，x(·)在Banach空间X上取值，A是解析算子族的无穷小生成元，设，f，g是下文合适定义的函数，。

可控性[9]是数学控制理论的基本概念之一，可控性理论在有限和无限维系统中都扮演重要的角色，从[10]中可以发现诸多学者在研究无限维积分微分方程的可控性的同时也指出了随机微分方程的可控性。最近，分数阶微分方程的可控性变得越来越活跃了，[11]在研究分数阶发展方程的完全可控性时所采用的技巧是分数阶积分解算子的性质和不动点原理。受上面文献的启发和激励，为了更进一步，本论述第三部分也研究了形式如

具有非局部初始条件的一类抽象分数阶积分微分发展方程的可控性，满足条件：是阶Caputo导数，x(·)在Banach空间X上取值。由L2（J,U）获得控制函数u(·)，满足U是一个Banach空间。B是一个从U到 X的有界线性算子，A是解析算子族的无穷小生成元。设，f，g是下文合适定义的函数。本论述通过使用适度解一个更普遍的概念，建立了方程（2）的可控性条件。

1　预备知识

本节介绍了贯穿全文的符号、定义、注释、引理，并且给出了方程（1）适度解[7]的定义，最后给出了证明主要结果用到的假设。

设C（J，X）是从J到X的连续函数的Banach空间，满足范数

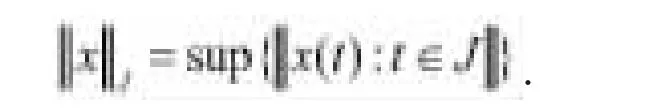
设B（X）表示从X到X的有界线性算子的Banach空间。

一个可测函数x:J→X是Bochner积分[13]，当且仅当是勒贝格可积的。

设L1（J，X）表示连续函数x:J→X（其中x是Bochner可积的）的Banach空间，满足对于所有的x∈L1（J，X），范数

L（X）表示从X到它自身的所有有界线性算子的空间，D（A）表示A的定义域，ρ（A）表示A的预解集。是一致有界线性算子紧解析半群的无穷小生成元，且设0∈ρ（A），R（λ，A）=（λI-A）-1代表A的预解算子。

定义1.1.[2]下限为a的p阶分数阶积分定义为：

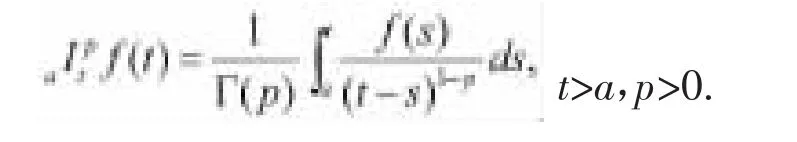
定义1.2.[2]p（p＞0）阶黎曼-刘维尔导数定义为：

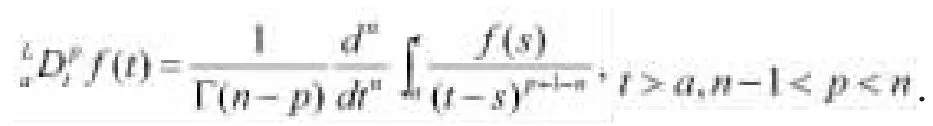
定义1.3.下限为a的p阶Caputo导数定义为：

如果f是X上取值的抽象函数，则定义1.1，1.2中的积分在Bochner意义下是可以取值的。

注释1.1.假设J⊂R和1≤p≤∞，对于可测函数m:J⊂R，定义范数

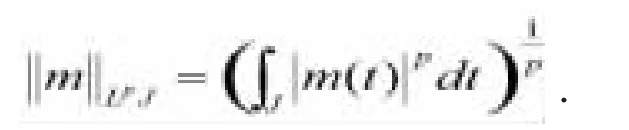
定义1.4.一个算子称为是扇形的，假如存在常数，且M＜0，使得A的预解存在于扇形的外部，满足

注释1.2.研究α（0＜α＜1）阶Caputo导数发展方程的柯西问题，形式如下：

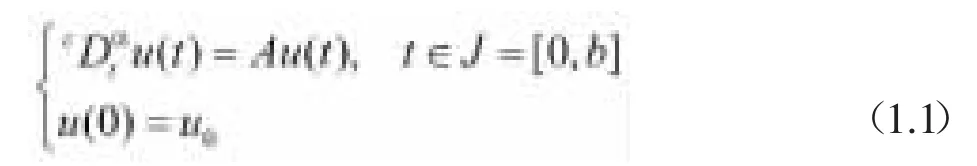
注释1.3.[14]假如是模型（1.1）的一个解算子，则

现在我们讨论模型（1）适度解的定义。

根据定义1.1和1.2，在方程（1.2）积分存在的条件下，变换非局部柯西问题（1）为如下等效的积分方程

引理1.2.假设方程（1.2）成立，且A是一个扇形算子，则有

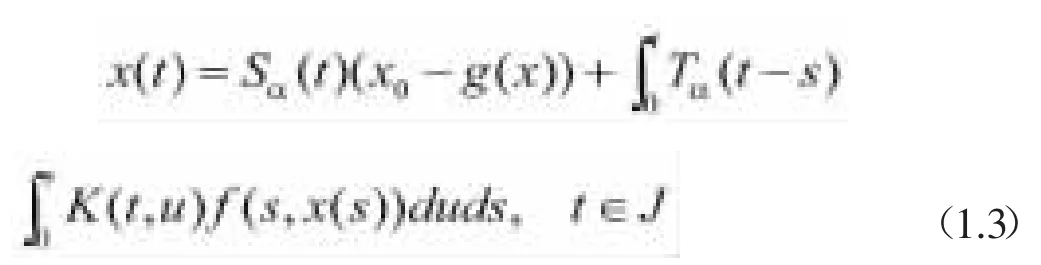
满足

引理1.4.[1]如果以及，则对于任意的t>0，有

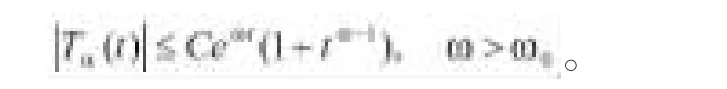
引理1.6.（Krasnoselskii不动点定理）设E是一个Banach空间，令B是E的一个有界闭凸子集。设F1与F2是B到E的压缩，使得对于每一个x，y∈B，有F1x+ F2y∈B，如果F1是压缩的，F2是完全连续的，则方程F1x+F2y＝x在B上有一个解。

定义1.6.函数x:J→X称为是方程（1）的适度解，假设x满足如下方程

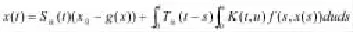
其中

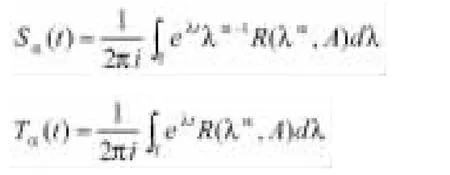
注释1.5.假设在方程（1）中产生一个C0-半群，则得到

定义1.7.方程（1）称为是在J上可控的，假如对于每一个，存在一个控制函数，使得方程（1）的一个适度解x满足x（b）=x1.

本节给出如下的假设：

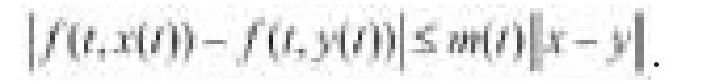
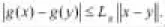
显然，若果(H2)成立，那么下面的假设成立：

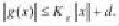
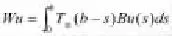
(H6)映射t→Kt从J到是连续的，此处

2　可解性与可控性结果

满足的条件下，方程（1）在J上有一个适度解。

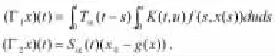
为了使如下过程更清楚，分几步证明。

由压缩γ＜1得到k0＞0,使得对于，有

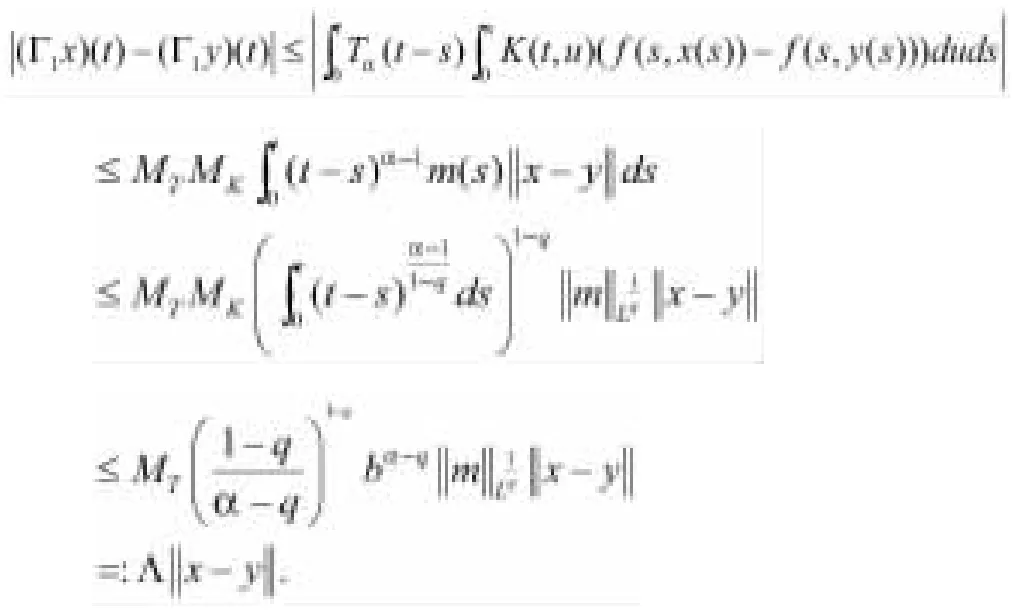
由压缩γ＜1,获得Λ＜1,这暗示Γ是一个压缩映射。

步骤三.Γ2是一个完全连续的算子,也分几步证明

首先,证明Γ2在上是连续的。对于,设.由（H’2），当n→∞,得到g（xn）→g（x）进一步得到

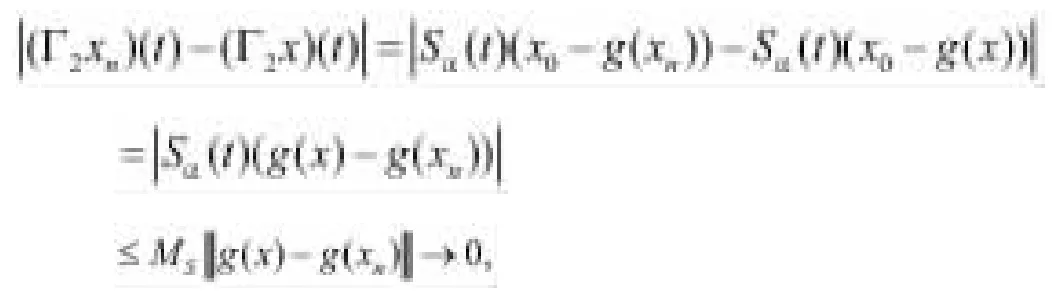
这暗示Γ2是连续的。

定理2.2如果(H1-H2),(H4-H6)是满足的，则在和

满足的条件下，方程（2）在J上是可控的。

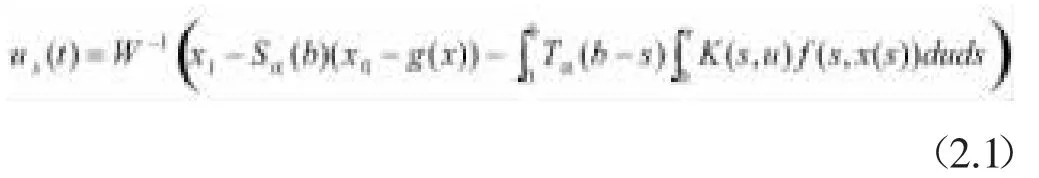
可以得到控制函数ux（t）．通过

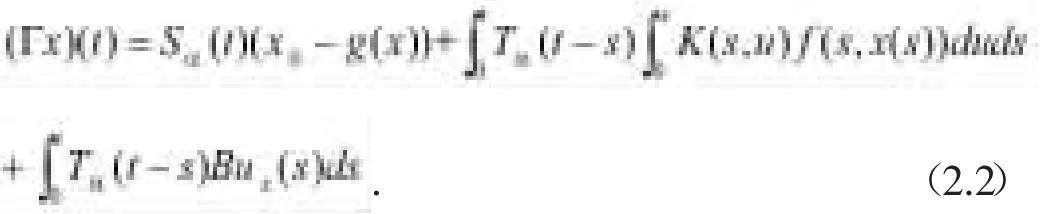
证明使用控制函数ux（t），算子Γ在C（J，X）上有一个不动点x，这个不动点是方程（2）的一个适度解。显然，这意味着ux在有限时滞b上控制着从x0到x1的适度解x，这暗示了方程（2）在J上是可控的。

由方程（1.4），得到

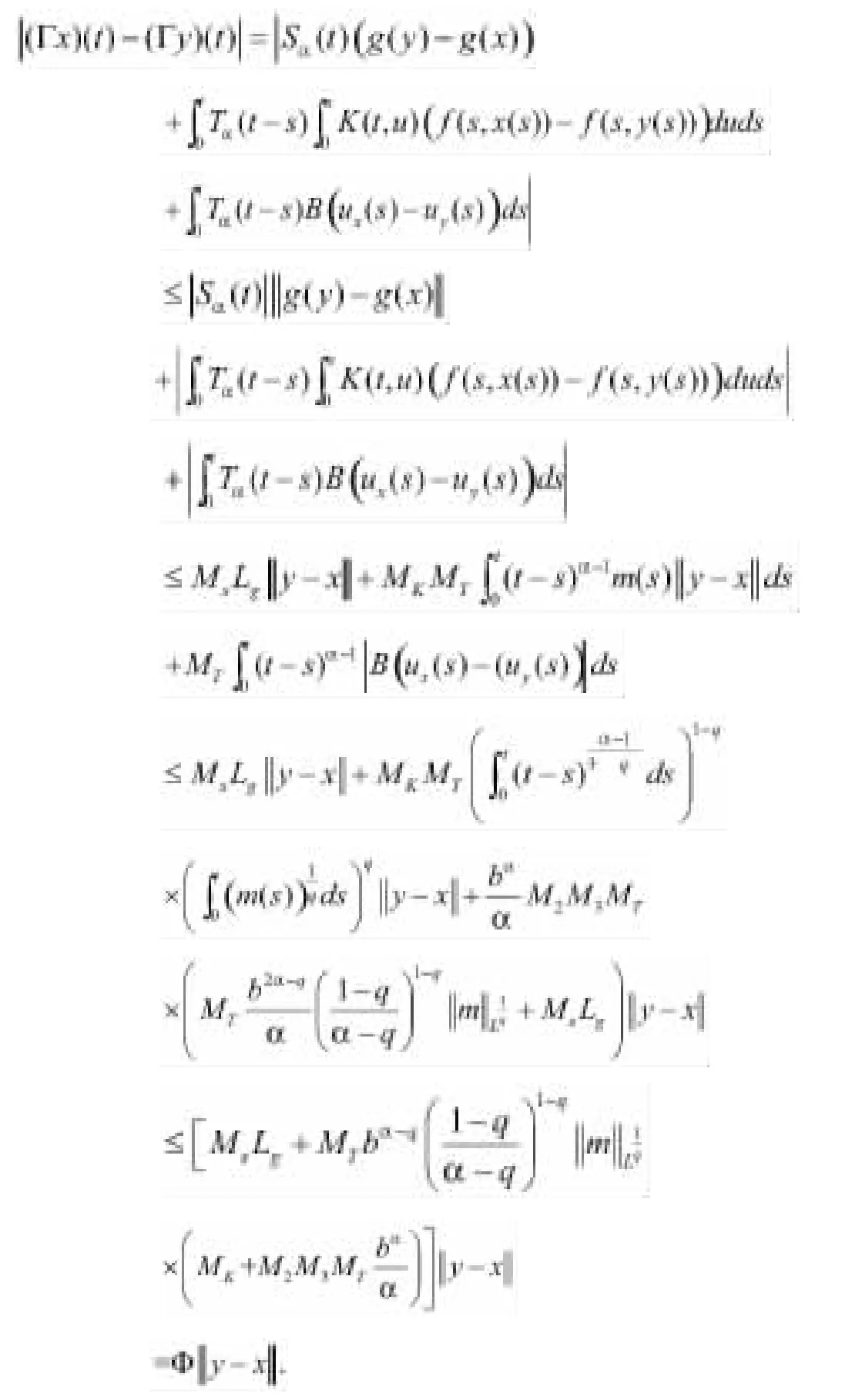
因此，Γ是一个压缩映射，并且有一个不动点x*∈C（J，X），所以此x*是方程（2）的一个适度解，因此方程（2）在J上是可控的．证明完毕。

3　应用举例

此处举例讨论了定理2.1的一个简单应用，研究了形式为

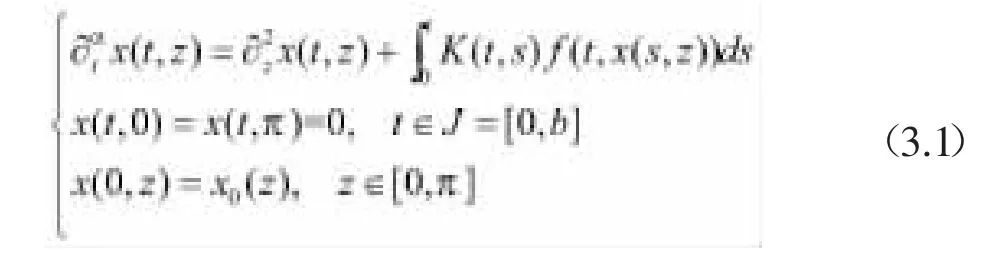
的分数阶偏积分微分方程，满足∂αt是阶Caputo分数阶偏导数，f是已知函数，

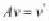
所得到的，所以（H4）是满足的。

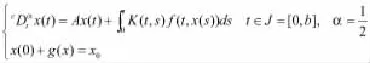
因此由定理2.1，如果（H1-H6）是满足的，则方程（1）在[0，b]上是可解的．证明完毕。

参考文献：

［1］K.S.Miller and B.Ross.An introduction to the fractional calculus and differential equations［M］.John Wiley and Sons, New York,NY,USA，（1993）.

［2］I.Podlubny.Fractional differential equations［J］.Academic Press,San Diego,Calif,USA,198（1999）：1-13.

［3］H.J.Lee,J.Park and J.Y.Park.Existence results for secondorder neutral functional differential and integrodifferential inclusions in Banach spaces［J］.Math.Phys.2000（2002）：1-13.

［4］K.Karthikeyan.Existence results for impulsive differential and integrodifferential equations and inclusions［M］.Bharathiar University,India，（2010）：58-70.

［5］X.B.Shu,Y.Lai and Y.Chen.The existence of mild solutions for impulsive fractional partial differential eqtations［J］. Nonlinear.Anal.74（2011）：2003-2011.

［6］E.Hernándea,D.O'Regan and K.Balachandran.On recent developments in the theory of abstract differential equations with fractional derivatives［J］.Nonlinear.Anal.73（2010）：3462-3471.

［7］Y.Zhou and F.Jiao.Existence of mild solutions for fractional neutral evolution equations［J］.Compute.Math.Appl.59 （2010）：1063-1077.

［8］G.M.Mophou.Existence and uniqueness of mild solutions to impulsive fractional differential equations［J］.Nonlinear.Anal. 72（2010）：1604-1615.

［9］X.B.Shu and Q.Wang.The existence and uniqueness of mild solutions for fractional differential equationswith nonlocal conditions of order［J］.Compute.Math.App.64（2012）：2100-2110.

［10］Y.K.Chang,J.J.Nieto and W.S.Li.Controllability of semilinear differential systems with nonlocal initial conditions in Banach spaces［J］.Optim.Theory.Appl.142（2009）：267-273.

［11］K.Balachandran and J.P.Dauer.Controllability of nonlinear system in Banach spaces:A survey［J］.Optim.Theory.Appl.115（2002）：7-28.

［12］X.Yang and H.B.Gu.Complete controllability for fractional

evolution equations［J］.Abstract and Applied Analysis. （2014）：Article ID 730695,8 pages.

［13］K.Yosida.Functional Analysis［M］.sixth ed.Springer, Berlin,1980.

［14］N.I.Mahmudov and S.Zorlu.On the approximate controllability of fractional evolution equations with compact analytic semigroup［J］.Compute.Appl.Math.259（2014）：194-204.

作者简介：高媛（1988-），女,汉族，甘肃张掖人，在读研究生，主要研究方向：分数阶积分微分方程的可解性。

收稿日期：2015-12-25

中图分类号：O175

文献标识码：A