基于参数规划的电网运行安全经济协调评估方法

赖晓文

(广东电网有限责任公司电力调度控制中心，广东 广州 510600)



基于参数规划的电网运行安全经济协调评估方法

赖晓文

(广东电网有限责任公司电力调度控制中心，广东 广州 510600)

摘要：提出一种基于参数线性规划的安全经济协调曲线生成方法，对电网运行状态进行定量评估。该方法分别将线路负载率和总购电成本作为系统运行的安全指标和经济指标，通过对电网运行优化模型中约束右端的含参量进行灵敏度分析，得到安全经济协调曲线，用以描述在给定条件下的电网最优运行状态，以及定量给出安全性与经济性之间的协调成本，同时还揭示了电网安全经济运行的可优化空间。

关键词：参数线性规划；电网运行评估；安全性；经济性；安全经济协调；理想运行度

电网优化运行最关键的目标之一是使得包括经济和安全在内的社会效益最大化。电网运行的经济性与安全性是一对矛盾统一体，表现在：一方面，提升安全裕度往往会降低电网运行的经济性；另一方面，经济性必须在确保安全性的前提下进行实现。近年来发生的若干停电事故表明，确保系统运行的安全性和可靠性就是对社会经济效益的重大贡献。因此，对电网运行进行安全与经济的协调是极有必要的，其中一个主要挑战在于定量评估分析这两个目标之间的替代效应，从而为电网的优化运行提供重要参考。

目前已有许多针对电网安全约束下经济运行的研究[1-4]，然而这些研究的重点主要集中在系统运行的经济效益上，而没有对安全效益与经济效益的协调和替代效应作进一步的分析。文献[5]对多级电力市场的建立进行了分析，并提出了基于交易排序的安全协调策略，该策略允许通过调整交易合同以保证整个电网的安全性。文献[6]介绍了在区域电力市场层面，市场交易与电网安全调度之间的内在关系与协调模式。文献[7]提出了对安全性与经济性进行平衡的电力系统调度的一般理论框架，但没有给出数学模型。文献[8]建立了一个多目标的线性规划模型以及基于安全性优先或经济性优先的模型解法，以联合分析有功潮流调度的经济特性与安全特性，但文中并没有提出电网运行的安全经济量化协调方法。

为了描述电网运行中安全性与经济性的矛盾，本文提出了基于参数线性规划的安全经济协调曲线评估方法。首先采用直流潮流模型，分别将线路负载率和总购电成本定义为系统运行的安全指标和经济指标；然后建立了考虑安全指标与经济指标的多目标优化模型，并利用ε约束法[9]将其等效地转化为直流最优潮流下的参数线性规划问题，转化后的模型中的主要优化目标为总购电成本最小，安全性不等式约束的右端值设为含参量以考虑不同的安全运行裕度水平；最后，通过求解参数线性规划问题可以得到量化描述安全指标与经济指标之间的协调关系的安全经济协调曲线(security-economy coordination curve，SECC)。基于此，本文提出了可以实现电网运行状态可视化的SECC分析法以及理想运行度的概念。该方法可以广泛用于电网对购电行为的开放性评估、电力系统调度效益评估、阻塞管理成本分析等方面。同时，基于国内某省级电网的实际运行数据进行了算例分析，算例给出了该电网的安全经济协调曲线，并解释了曲线在电网运行状态评估中的意义与应用，结果表明该方法能够有效应用于电网运行状态评估。

1安全经济协调运行模型

为了定量分析电网运行中安全性与经济性的协调和替代效应，需要定义能够反映安全与经济运行水平的指标。

1.1安全指标

将电网运行的安全指标L定义为所有输电线路的最大负载率，即：

(1)

(2)

式中：j为输电线路的编号；Ω为系统中所有输电线路的集合；Rj为输电线路j负载率的标幺值；Fj为j的有功潮流；Fj,max为j的有功潮流上限；λj为考虑了j特定条件(如距离、重要性等)的负载率修正因子。式(2)描述了每条输电线路直流潮流的负载程度以及可用程度。式(1)选取所有输电线路负载率标幺值的最大值作为全系统的安全性指标。经济学中的“木桶原理”为上述定义提供了有力的依据，即：即使其他线路的负载都非常轻，全系统的安全裕度仍然取决于负载最重的输电线路，安全指标L值越小，系统运行的安全水平越高。因此，系统运行的安全目标可表示为最小化输电线路的最大负载率，即

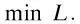
(3)

1.2经济指标

电网运行的经济性通常以总购电成本C来衡量，即

(4)

式中：i为机组的编号；U为系统中所有机组的集合；Pi为机组i的有功出力；fi(Pi)为i的购电成本函数。发电机组的成本函数通常为凸二次函数形式，故可采用分段线性的方法将其线性化，且不失一般性，本文假设每台机组的购电成本均为线性函数。与安全指标类似，经济指标C值越小，系统运行的经济效益越好。系统运行的经济目标可表示为最小化总购电成本，即

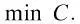
(5)

1.3参数线性规划模型

结合式(3)和式(5)，安全经济多目标优化模型可表示为如下形式：

(6)

式(6)是一个多目标规划模型，其两个目标在通常情况下是相互矛盾的，因此该模型并没有绝对的多目标最优解，只有帕累托最优解。当保持总效益最优时，该模型存在不同的帕累托最优解，这些解中安全效益与经济效益具有替代效应。

安全指标与经济指标具有不同的数量单位，且需要最小化最大线路负载率，因此无法直接对式(6)进行求解，可以采用ε约束法[9]对上述模型进行修改。ε约束法的核心思想是通过选取主要目标并将其他目标设为约束，使多目标规划模型转化为单目标规划模型。对式(6)应用ε约束法，原模型可以修改为如下形式：

(7)

(8)

其中，总购电成本作为主优化目标，而线路负载率标幺值的最大值则由变量ε进行约束。可进一步将式(8)转化为一组安全性不等式约束，如下：

(9)

综上分析，考虑安全经济协调的电网优化运行模型可以等效为如下的参数线性规划模型(parametriclinearprogramming，PLP)：

(10)

(11)

(12)

(14)

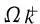
上述模型与常规的直流最优潮流问题相似，但不同之处在于不等式约束的右端加入了参量ε，以考虑不同的安全运行裕度要求。通过求解不同安全裕度要求(改变ε值)下的经济最优运行点，即能定量分析安全指标与经济指标的协调与替代效应。

2安全经济协调曲线的生成

本文所述PLP模型的求解过程主要分为三个步骤：第一，求得参数ε的有效上界；第二，通过灵敏度分析方法定位ε的关键临界值，在关键临界点处求解PLP模型；第三，根据求解得到的关键临界点绘出安全经济协调曲线。

2.1求参数ε的有效上界

在一定的负荷分布状态下，无论如何调度发电机组，输电线路的负载率总是存在一个最小值Lmin，因而参数ε是有下界的。但是计算ε的下界比较复杂，需要进行穷举计算。事实上，ε同时还具有有效上界，它表示在合理的调度方式下输电线路的最大负载率。在合理的方式下，当系统的经济效益最大时，线路负载率将达到有效上界。根据这一点可以通过优化系统运行成本得到ε的有效上界，该上界将在后续的参数规划分析中作为ε的初值。

采用单纯形法求解式(10)、(12)至(14)构成的模型，从而得到参数ε的有效上界。求解结果对应全局最小购电成本Cmin和全局最大负载率Lmax。

2.2求解参数线性规划模型

为了得到参数ε变化时的最优目标值C，需要从ε=Lmax开始不断减小ε值，同时求解式(10)至(14)构成的模型。这个过程将采用带有单个约束右端参数的线性规划灵敏度分析方法，从而计算出最优基和最优解发生变化时ε的关键临界值。带有单个约束右端参数的线性规划灵敏度分析法详见文献[10-11]。图1为求解模型的流程。

图1　参数线性规划模型求解流程

2.3绘制安全经济协调曲线

在灵敏度分析完成后，可以得到一系列临界最优运行点(L，C)。原问题是线性的，同时单纯形法中的最优基在两个相邻的ε临界值之间保持不变，故最优解和目标函数值也是线性变化的。因此，只需在二维坐标系中将临界最优运行点用线段连接起来即可得到连续的SECC，如图2所示。

图2　典型的电网安全经济协调曲线

为了使安全指标与经济指标具有可比性，分别对这两个指标进行以下归一化处理。

(15)

(16)

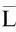
3安全经济协调曲线在电网运行评估中的应用

3.1特征与经济意义

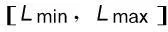
SECC与经济学中代表消费者偏好的无差异曲线十分相似。无差异曲线(如图3所示)上的点表示为消费者提供相同效用的所有可能的两种商品的组合。图3中，XA和XB分别是商品A和B的消费量。在曲线上的不同点，尽管A和B各自提供的效用不同，其总效用始终保持不变。与之类似，SECC上的每个点都是具有不同安全裕度和经济效益水平的帕累托最优解。

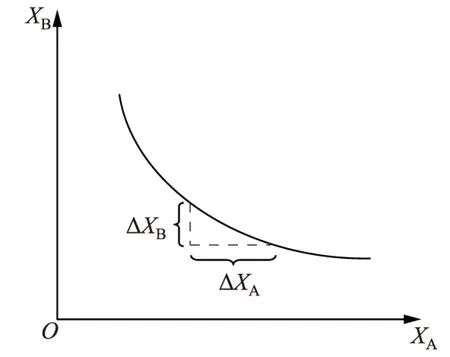
图3　经济学中的典型无差异曲线

经济学中，无差异曲线的梯度定义为边际替代率(marginal rate of substitution，MRS)。A对B的边际替代率rMRS,AB表示维持总的效用值不变时，增加一单位B的消费量需要减少的A的消费量。其计算公式如下：

(17)

与无差异曲线相同，SECC也是凸曲线，因而沿着曲线下移，其梯度的绝对值不断减小(边际替代率递减规律)。这表明，随着安全水平的不断提高，经济成本增加得越来越快；随着经济效益的不断提高，安全性也降低得越来越快。参照MRS，对协调成本(coordination cost，CC)进行定义：

(18)

协调成本定量描述了增加一单位安全效益(归一化后)所需的额外经济成本(归一化后)。

3.2基于安全经济协调曲线的事后评估法

美国东部电网电力市场于2008年提出了“理想调度”的概念，以追求电网运行的最优化。理想调度的主要目的在于辨识电网运行中安全性与经济性的缺陷，并通过分析历史运行状态发现可能的优化空间。SECC是对电网运行状况进行事后分析的一种有效手段。

由于负荷预测或潮流计算的误差，实际的电网运行状况通常与运行计划存在一定的偏差，这就导致电网运行在SECC右上方的非最优运行点。事后将电网实际运行状态与SECC进行比较，可以发现实际运行状态与理想运行状态之间的偏差。图4所示为实际电网运行中安全性与经济性缺陷及可优化空间示意图。

图4　实际电网运行中安全性与经济性缺陷及可优化空间

图4中，Pr是电网的实际运行点；Ps是与Pr具有相同购电成本Cr的安全最优运行点；Pe是与Pr具有相同最大输电线路负载率标幺值Lr的经济最优运行点。实际运行点与理想运行点之间的偏差计算如下：

(19)

(20)

式中：ΔL表示在不增加购电成本的前提下可以提升的系统安全裕度；ΔC表示在不降低系统安全效益的前提下可以节省的购电成本。这两个指标直观定量地表示了电网运行的安全效益与经济效益的可提升空间。

3.3理想运行度

为了比较不同调度员或不同负荷状况下的电网运行状态，这里进一步定义了“理想运行度”指标，它表示电网实际运行点与SECC上最近的安全经济协调最优运行点之间的偏差。实际运行点Pr的理想运行度D计算如下：

(21)

式中：p为SECC上的运行点；Λ为SECC上所有运行点的集合；Lp为SECC上运行点p的L值；Cp为SECC上运行点的C值。需要注意的是，式(20)中的所有值都已经在第3节的求解过程中进行了归一化处理。

图5所示为电网理想度示意图，其中，过Pr作SECC的垂线交于点PD，理想运行度即为Pr与PD之间的距离。在对不同调度员的绩效进行比较，以及对电网运行效益提升成果进行评估时，理想运行度可以作为一个科学有效的参考指标。

图5　电网理想运行度

4算例分析

本文基于国内某省级电网的实际数据对所述方法的有效性进行验证。该电网的主要参数包括：发电机组数111，输电线路数807，节点数532，有功负荷22 956.8 MW。所有输电线路的负载率修正因子λj均设为1.0，所有发电机组的二次购电成本函数均分为5段进行线性化处理。

首先，求解式(10)、(12)至(14)构成的模型，得到参数ε的有效上界，即全网最大负载率Lmax，本算例中，Lmax=0.925 9。第二步，以ε=Lmax为初始值，不断减小临界ε值，求解PLP模型直到不存在可行解。根据求解结果得到该电网的SECC，其中：Lmin=0.830 3，Lmax=0.925 9，Cmin=8 200 198.35，Cmax=8 202 629.43。归一化处理后的实际运行点与安全经济最优运行点的偏差计算结果为：ΔL=0.038 3，ΔC=1 234.92元。

上述结果表明：在不增加总购电成本的前提下，可以将输电线路最大负载率的标幺值减小0.0383；在不加重输电线路负载程度的前提下，可以将总购电成本减小1 234.92元。此外，计算出理想运行度D=0.341 3。指标越小，电网运行效益越好，该指标可以用于不同调度员或者电网历史运行状态的绩效比较。

5结束语

本文基于参数线性规划，提出了可用于对电网运行状态进行安全经济协调评估的方法。该方法包括三个步骤：定义安全指标和经济指标，用灵敏度分析法求解参数线性规划模型，以及绘制安全经济协调曲线。

为了确保该方法的可行性，本文假设购电成本函数是线性或分段线性的，该假设没有改变问题的本质。安全经济协调曲线与经济学中的无差异曲线十分相似，均为凸曲线，且服从边际替代率递减规律。根据这一特点，对协调成本进行了定义。安全经济协调曲线可以辨识电网运行中安全性与经济性的缺陷，发现可能的提升空间，从而为电网运行提供重要参考。基于安全经济协调曲线定义的理想运行度指标可以对不同调度员或不同负荷状况下的电网运行状态进行比较评估。

以国内某省级电网的实际数据为例，对该方法的有效性进行了验证。该方法能够为电网优化运行提高科学、合理和有效的参考，适用于电网运行状态的评估。

参考文献：

[1] ELACQUA A J, COREY S L. Security Constrained Dispatch at the New York Power Pool[J]. IEEE Transactions on Power Apparatus and Systems, 1982, PAS-101(8): 2876-2884.

[2] 夏清，张伯明，康重庆，等.电力系统短期安全经济调度新算法[J]. 电网技术，1997(11)：61-65.

XIA Qing, ZHANG Boming, KANG Chongqing, et al. A Novel Algorithm on Power System Short Term Economic and Security Dispatch[J]. Power System Technology, 1997(11): 61-65.

[3] 张宁，陈慧坤，骆晓明，等.广东电网节能发电调度计划模型与算法[J]. 电网技术，2008(24)：11-15.

ZHANG Ning, CHEN Huikun, LUO Xiaoming, et al. Model and Algorithm of Energy-conservation Based Generation Dispatching for Guangdong Power Grid[J]. Power System Technology, 2008(24): 11-15.

[4] 陈之栩，谢开，张晶，等.电网安全节能发电日前调度优化模型及算法[J]. 电力系统自动化，2009，33(1)：10-13，98.

CHEN Zhixu, XIE Kai, ZHANG Jing, et al. Optimal Model and Algorithm for Day-ahead Generation Scheduling of Transmission Grid Security Constrained Convention Dispatch[J]. Automation of Electric Power Systems, 2009, 33(1): 10-13, 98.

[5] BO R, LI Y, LIU F B. A Novel Coordination Scheme of Transaction Scheduling in Multi-level Power Market[C]//IEEE Power Engineering Society Transmission and Distribution Conf.,Dallas, USA:IEEE,2003.

[6] 夏清，彭涛，江健健.兼顾经济协调发展和电网安全的区域共同市场[J]. 电力系统自动化，2004，28(19)：1-5.

XIA Qing, PENG Tao, JIANG Jianjian. Regional Layered Electricity Market Considering Economical Coordination and Power Grid Security[J]. Automation of Electric Power Systems, 2004, 28(19): 1-5.

[7] 尚金成，周劼英，程满. 兼顾安全与经济的电力系统优化调度协调理论[J]. 电力系统自动化，2007，31(6)：28-33.

SHANG Jincheng, ZHOU Jieying, CHENG Man. Coordination Theory of Electric Power System Optimal Dispatch Considering Security and Economics[J]. Automation of Electric Power Systems, 2007, 31(6): 28-33.

[8] 江长明，朱继忠，徐国禹. 有功调度中经济性与安全性的协调问题[J]. 电力系统自动化，1995，19(11)：43-48.

JIANG Changming, ZHU Jizhong, XU Guoyu. The Coordination of Economic Characteristic and Security in Real Power Dispatching[J]. Automation of Electric Power Systems, 1995, 19(11): 43-48.

[10] GAL T. Linear Parametric Programming-A Brief Survey, in Sensitivity, Stability and Parametric Analysis[M]. Berlin: Springer, 1984.

[11] GAL T. Postoptimal Ananysis, Parametric Programming and Ralated Topics[M]. New York: McGraw-Hill, 1979.

赖晓文(1988)，男，广东惠州人。工学博士，从事电力系统发电调度工作，主要研究方向为电力系统优化调度、电力系统运行评估等。

(编辑查黎)

Evaluation Method for Security-economy Coordination for Power Grid Operation Based on Parameter Planning

LAI Xiaowen

(Electric Power Dispatching Control Center of Guangdong Power Grid Co., Ltd., Guangzhou, Guangdong 510600, China)

Abstract：A kind of generation method for security-economy coordination curve based on parameter linear planning is proposed to carry out quantitative evaluation on power grid state. This method takes line load rate and total electricity purchasing cost as security index and economy index for system operation. By analyzing sensitivity of containing parameters at the constraint right end in the power grid operation optimization model, security-economy coordination curve is obtained to describe optimal operational state of the power grid under given conditions, quantificationally provide coordination cost for security and economy and reveal optimizable space for safe and economic operation of the power grid.

Key words：parameter linear planning; power grid operation evaluation; security; economy; security-economy coordination; ideal operation degree

作者简介：

中图分类号：TM734

文献标志码：A

文章编号：1007-290X(2016)02-0048-06

doi:10.3969/j.issn.1007-290X.2016.02.010

收稿日期：2015-09-06修回日期：2015-11-17