光伏电池的建模与光伏发电系统的仿真

陈杏灿，程汉湘，彭湃，杨健

(广东工业大学 自动化学院，广东 广州 511400)



光伏电池的建模与光伏发电系统的仿真

陈杏灿，程汉湘，彭湃，杨健

(广东工业大学 自动化学院，广东 广州 511400)

摘要：利用光伏电池的数学模型，使用修正参数得到不同环境下的性能参数，在MATLAB/Simulink环境中搭建光伏电池仿真模型，并对不同光照强度和不同环境温度下的光伏电池输出特性进行分析比较。基于电导增量法与升压斩波电路，对任意给定的不同光照强度和不同环境温度下的光伏发电系统进行仿真分析。仿真结果表明，该模型可实现光伏发电系统的最大输出功率跟踪，验证了该模型可满足光伏发电系统的仿真需要。

关键词：光伏电池；光伏发电系统；MATLAB/Simulink；最大功率跟踪

由于化石能源日益枯竭，而太阳能资源丰富，且分布广泛，利用太阳能发电是解决当前能源紧张的重要途径，同时太阳能发电也是目前最清洁的发电技术，许多国家已经开始研究和利用太阳能发电。我国在2007年颁布的《可再生能源中长期发展规划》中指出，将积极促进太阳能发电技术的发展，做好太阳能发电技术的战略储备[1]。太阳能发电已经成为电力行业中新能源发电领域的研究热点，具有较大的发展前景。

光伏电池的输出特性是太阳能发电的最基本研究内容，文献[2]建立的光伏模型是基于大量实验数据拟合的，文献[3]采用分段多项式拟合法建立光伏模型，上述模型能较好地复原光伏电池的内部结构，精度较高，但由于光伏电池内含有PN结(positive and negative junction)，模型中的参数较难确定，不利于工程应用。

本文利用MATLAB/Simulink工具包里的仿真模块和S函数编程，通过引入修正参数得到不同光照强度和环境温度下的性能参数，搭建光伏电池与光伏发电系统的仿真模型，仿真并分析光伏电池的输出特性，同时基于电导增量法与升压斩波电路实现光伏输出的最大功率跟踪，通过给定不同光照强度与环境温度，验证光伏发电系统最大功率跟踪的有效性。

1光伏电池的数学模型与输出特性

图1是光伏电池的等效电路[4]。

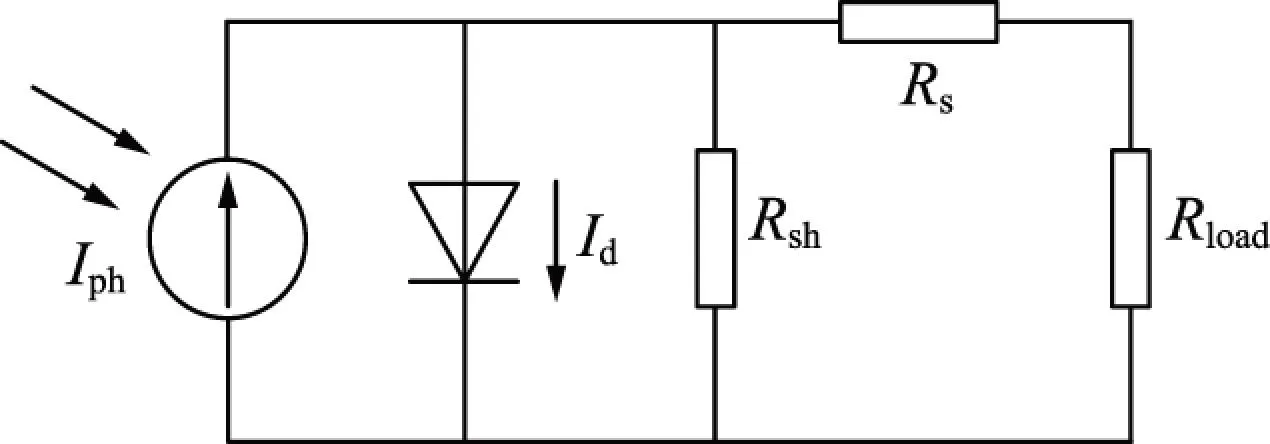
Iph—光生电流；Id—反向饱和电流；Rsh—旁路电阻；Rs—串联电阻；Rload—负载电阻。图1　光伏电池的等效电路

图1中，当光照为恒定时，因光伏电池的光生电流不随工作状态而改变，可将其等效为一个恒流源。该模型可准确反映电池在不同环境下的输出特性，但模型中的光生电流、反向电流，PN结系数等参数[5]与外特性没有一一对应关系，较难通过实际测量获取。而在实际应用中，光伏电池的短路电流Isc、开路电压Uoc、最大功率电压Um和最大功率电流Im这4个参数与输出特性密切对应，电池厂商均会提供标准环境下的这4个参数。且因光伏电池是一种能将半导体材料的电子特性转换成电能的固态器件，根据光伏电池的工作原理可以建立光伏电池的数学模型[6-8]，式(1)—(3)是光伏电池的电压-电流(U-I)输出特性公式[9]：

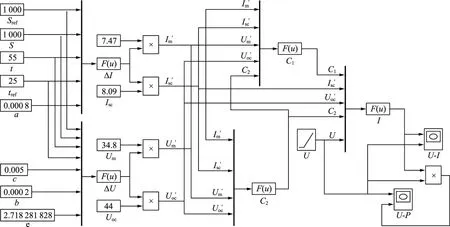
图2　光伏电池基本模型

(1)

(2)

(3)

式(1)—(3)中：U、I为电池输出的电压和电流；C1、C2为修正系数。

由于该模型仍然存在缺陷，可根据实际光伏电池的标准性能参数将不同光照和温度下的参数进行拟合，得到式(4)和式(5)的修正系数[10]，代入式(6)可得到修正标准条件下的4个性能参数，再将修正后的4个性能参数重新代回式(1)—(3)，就可以得到任意条件下的光伏电池输出特性。

(4)

(5)

(6)

式(4)—(6)中：S为光照强度，Sref为标准条件下的光照强度；t为温度，tref为标准条件下的温度；a、c为温度补偿系数，b为光强补偿系数；I′sc、U′oc、I′m、U′m分别为修正标准条件下的短路电流、开路电压、最大功率电流和最大功率电压。

按式(1)—(6)与给定的4个性能参数，在MATLAB/Simulink环境下，搭建光伏电池的模型。其中，补偿系数取a=0.000 8，b=0.000 2，c=0.005；4个性能参数取实际光伏电池的标准性能参数[11]，Isc=8.09 A，Uoc=44 V，Um=34.8 V，Im=7.47 A；设标准条件下的光照强度Sref=1 000 W/m2，标准条件下的温度tref=25 ℃。模型如图2所示。

图2中，F(u)为Simulink自带的函数模块，由图2给定不同光照强度与不同环境温度，得到不同的U-I特性曲线和电压-功率(U-P)特性曲线，如图3所示。

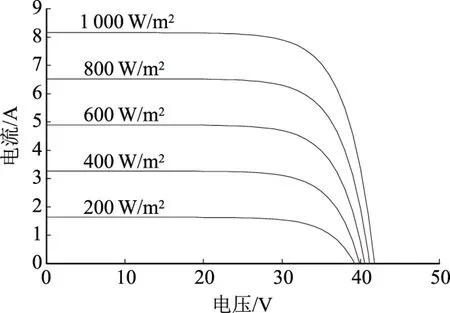
(a)不同光照强度下的U-I曲线

(b)不同光照强度下的U-P曲线

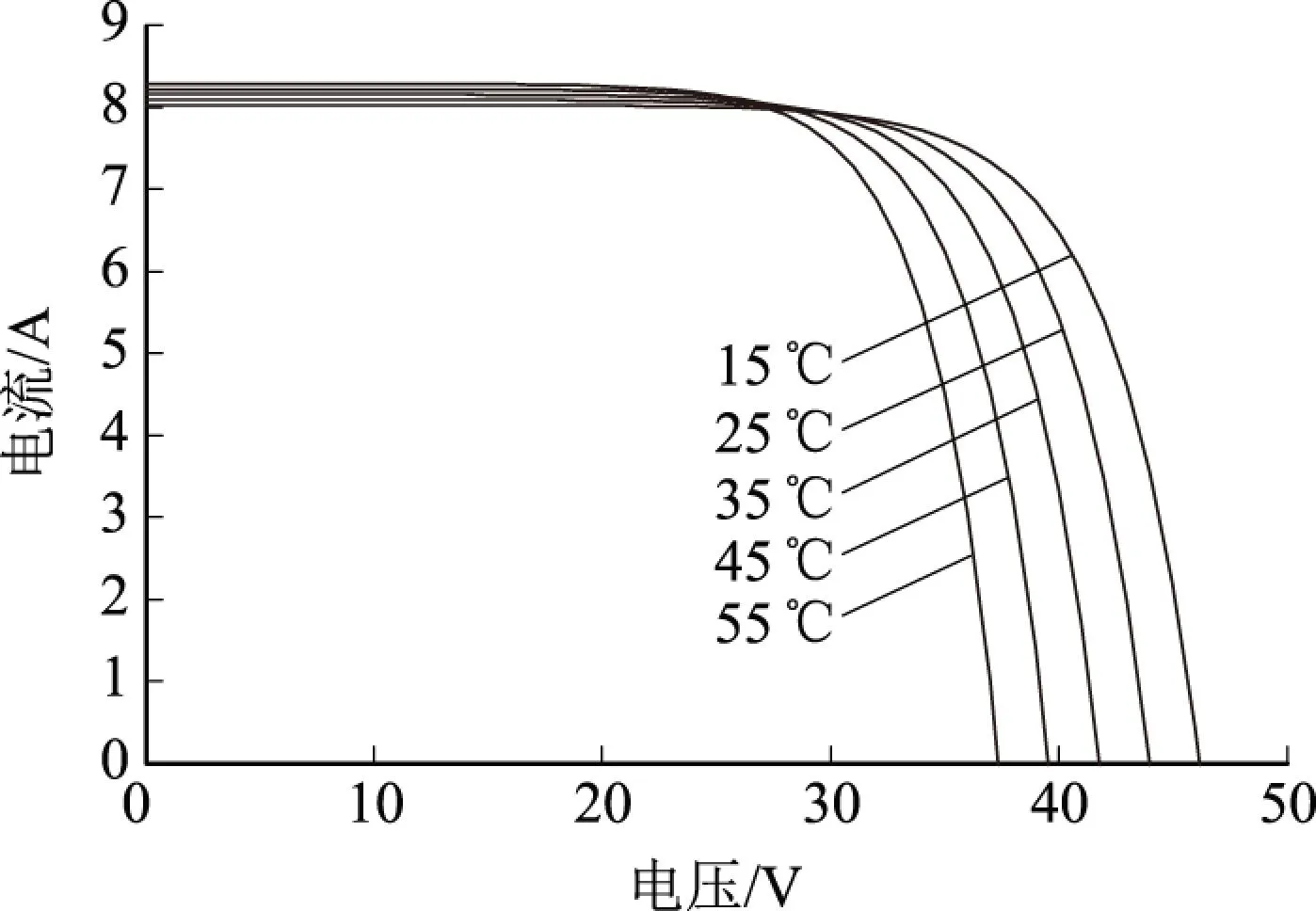
(c)不同温度下的U-I曲线

(d)不同温度下的U-P曲线图3　光伏电池输出特性曲线

图3(a)和图3(b)中，给定温度为35 ℃不变且光照强度分别为200 W/m2、400 W/m2、600 W/m2、800 W/m2和1 000 W/m2时，得到不同的U-I和U-P曲线，由图3(a)可看出，在输出电压相同的情况下，随着光照强度增大，输出电流增大；由图3(b)可看出，在输出电压相同的情况下，随着光照强度增大，功率增大。因此，日照强度的大小与光伏电池的输出电流和输出功率成正比。图3(c)、3(d)中给定光照强度为1 000 W/m2不变，温度分别为15 ℃、25 ℃、35 ℃、45 ℃和55 ℃，得到不同温度下的U-I和U-P曲线。图3(c)中，在输出电流相同的情况下，随着温度增加，输出电流减小；图3(d)中，在输出功率相同的情况下，随着温度增加，输出功率减小。因此，环境温度的大小与光伏电池的输出电流和输出功率成反比。

T—温度；C、C1—电容；L—电感；R—负载电阻；D—二极管；g—IGBT的驱动端；PWM—脉宽调制技术，pulse width modulation的缩写。图5　光伏发电系统图

图3(a)和图3(b)中，给定温度为35 ℃不变且光照强度分别为200 W/m、400 W/m、600 W/m、800 W/m和1 000 W/m时，得到不同的U-I和U-P曲线，由图3(a)可看出，在输出电压相同的情况下，随着光照强度增大，输出电流增大；由图3(b)可看出，在输出电压相同的情况下，随着光照强度增大，功率增大。因此，日照强度的大小与光伏电池的输出电流和输出功率成正比。图3(c)、3(d)中给定光照强度为1 000 W/m不变，温度分别为15 ℃、25 ℃、35 ℃、45 ℃和55 ℃，得到不同温度下的U-I和U-P曲线。图3(c)中，在输出电流相同的情况下，随着温度增加，输出电流减小；图3(d)中，在输出功率相同的情况下，随着温度增加，输出功率减小。因此，环境温度的大小与光伏电池的输出电流和输出功率成反比。

由仿真波形可看出，光伏电池的输出特性是呈非线性的，而为了获得光伏电池的最大效率，需要对光伏电池的输出功率进行跟踪控制，使得在不同光照强度和不同环境温度下，光伏电池的输出功率达到最大。

2最大功率跟踪控制

从图3可以看出，给定的光照强度和环境温度不同时，输出的U-P曲线均不相同，但每个曲线均存在唯一一个最大功率点。为了提高光伏电池输出能量的转化率，希望始终使光伏电池保持工作在最大功率点附近，因此需要使用最大功率跟踪算法来控制光伏发电系统[12]。

本文采用的是电导增量法的最大功率跟踪(maximum power point tracking，MPPT)控制，根据光伏电池的输出特性U-P曲线为一阶连续可导曲线，可通过一阶导数的极值，求得输出电导的变化量和瞬时电导的值，决定参考电压Uref的变化方向，使光伏电池工作在最大功率点附近。使用MATLAB/Simulink工具箱中的S函数编程实现该算法。以光伏电池的电压与电流为输入量、参考电压Uref为输出量，流程图如图4所示。

U(k)、I(k)为k 时刻光伏电池的电压和电流。图4　电导增量法的流程图

在k-1时刻，参考电压Uref的变化方向取决于k时刻的瞬时负电导值和电导变化率的大小关系，而与k-1时刻的工作点无关，因而该算法可在光照强度变化较快的场合实现高精度控制。

3光伏发电系统的仿真分析

为证明上述光伏电池模型可以应用于光伏发电，在MATLAB/Simulink环境下，搭建如图5所示的光伏发电系统。图5中，光伏电池的输入量为光照强度、环境温度、标准条件下的4个性能参数以及端电压，用式(1)—(6)仿真得到的电流作为受控电流源的控制量，经升压斩波电路将电压提升，同时为了提高发电效率，充分利用光伏阵列所产生的能量，且由于光伏电池输出的直流电不是很稳定，输出功率也会受到光照强度和环境温度的影响，不能直接供给负载使用，因此系统要能实现实时追踪光伏阵列的最大功率点，通过斩波电路与MPPT控制，将光伏电池输出的直流电变换为稳定可调的直流电，使之工作在最大功率点处。仿真以电阻负载为例，通过改变光照强度和环境温度的值，来观察负载两端电压波形变化。

根据图5,在MATLAB/Simulink环境中搭建仿真模型，模型中，滤波电容C设值为100 F，用于储存电能用的电感L设值为10 mH，用于保持输出电压的电容C1设值为300 F，负载电阻R取50 Ω。同时，设置输入的光照强度在0时刻为800 W/m2，环境温度为25 ℃；经过0.2 s后，光照强度降低为600 W/m2，环境温度降为15 ℃；再经过0.2 s后，光照强度升高到1 000 W/m2，环境温度升为35 ℃。以此来验证不同光照强度和不同环境温度下，光伏发电系统能否跟踪最大功率点变化，始终保持在最大功率点附近工作。仿真结果如图6所示。

由图6(a)电流波形与图6(b)电压波形可以看出，光伏电池从0时刻开始工作，因光伏电池内部存在电感电容，刚上电时的充电过程造成光伏电池的输出扰动较大，经最大功率跟踪控制，约0.05 s后电流和电压均趋于稳定；同时，由于设置在0.2 s处光照强度跟环境温度突然降低，可以看出输出的电流和电压均发生了改变，虽然经过一小段过渡过程，但最后均再次趋于稳定；同理，在0.4 s时，由于再次改变环境因素，光伏电池同样出现扰动后趋于稳定状态；之后，只要保持光照强度与环境温度不变，输出电压、电流均不再发生变化。由图6(c)可看出，输出功率也随外界环境因素的变化而变化，在0.4 s后，由于光照强度为1 000 W/m2，环境温度为35 ℃，输出功率与电压、电流一样，经过小段波动后趋于稳定，最终保持在最大功率点250 W左右，与图3中光照强度为1 000 W/m2、环境温度为35 ℃的U-P曲线的最大功率点相同。因此，在改变不同环境因素时，输出功率都可保持在最大功率点附近。这些波动是由MPPT控制采用扰动观察法导致的，从参考电压波形可以看出MPPT控制算法始终通过扰动电池输出电压寻找最大功率点。由图6(d)的负载电压波形可以看出，只要光照强度与环境温度为恒定值，光伏电池的输出电压均趋于稳定，能向电阻负载提供稳定的直流。

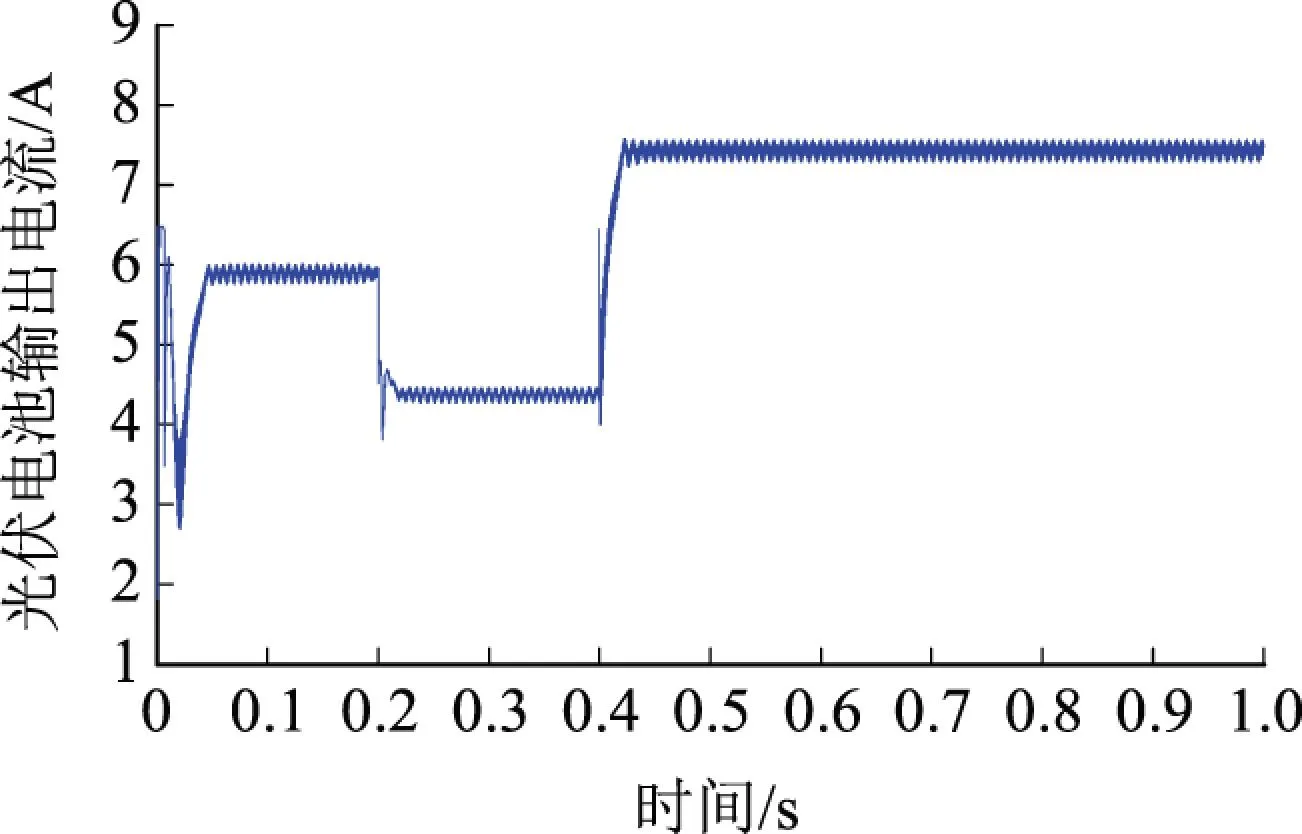
(a)输出电流波形

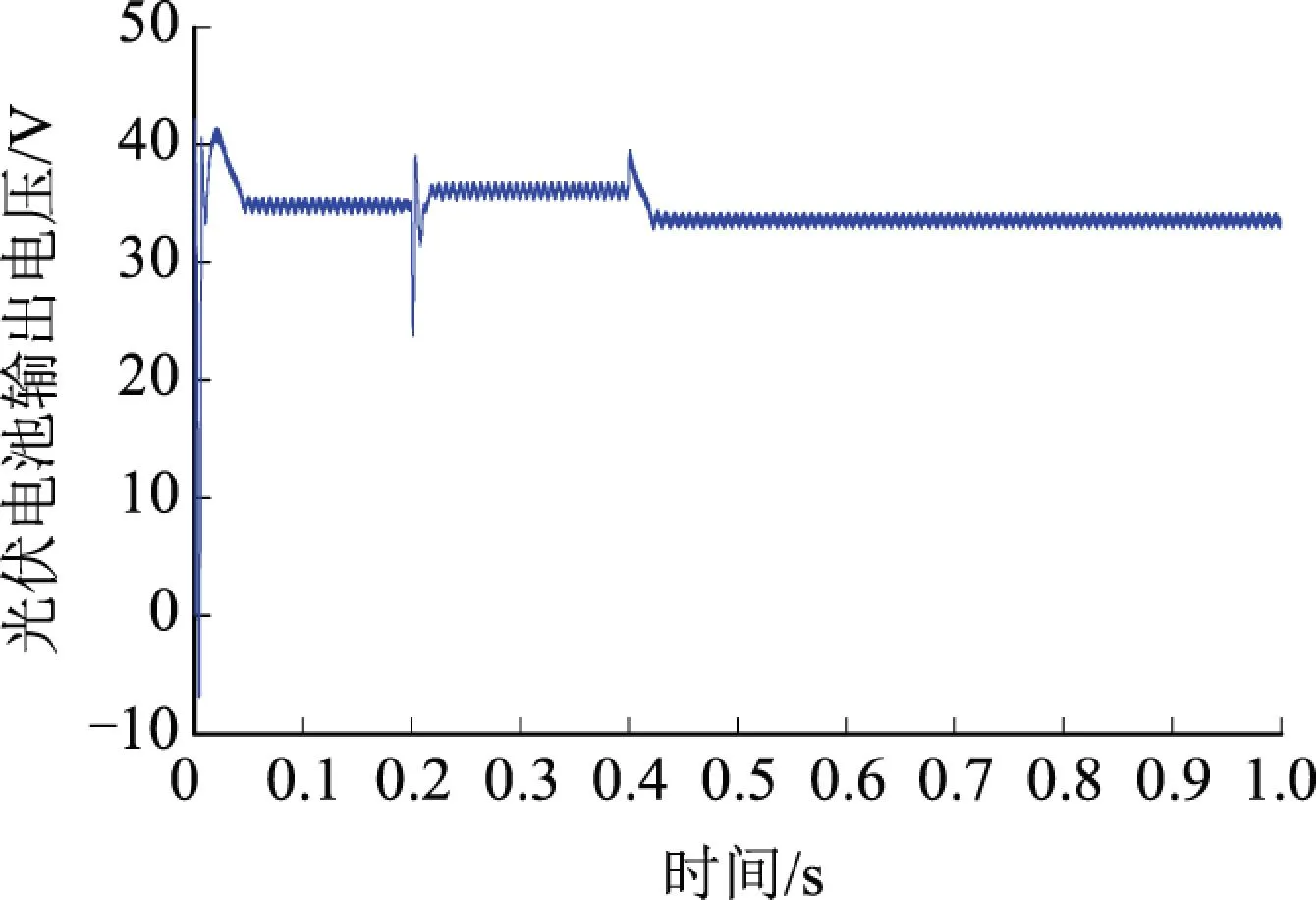
(b)输出电压波形

(c)输出功率波形

(d)负载电压波形图6　光伏发电系统工作波形

光伏并网发电系统的仿真结果，证明了基于性能参数的环境修正电池模型能够较好地模拟实际电池在不同环境下的输出特性，满足光伏发电系统的仿真要求。

4结束语

本文通过分析光伏电池的数学模型，使用环境修正系数得到光伏电池的性能参数，在MATLAB/Simulink环境下，搭建了光伏电池的仿真模型，通过斩波电路与最大功率跟踪控制，实现光伏发电系统的仿真。通过仿真得到的波形，分析光伏电池的输出特性和光伏发电的工作过程。通过试验给定不同的环境因素来验证光伏电池的静态及动态性能，表明该模型可满足光伏发电系统的仿真需要。

参考文献：

[1] 国家发展和改革委员会. 可再生能源中长期发展规划[J]. 可再生能源，2007，25(5)：1-5.

National Development and Reform Commission. Long Term Renewable Energy Development Plan[J]. Renewable Energy Resources，2007，25(5)：1-5.

[2] 江小涛，吴麟章，王远，等. 硅太阳电池数学模型[J]. 武汉科技学院学报，2005，18(8)：5-8.

JIANG Xiaotao，WU Linzhang，WANG Yuan，et al. Mathematical Model of Silicon Solar Cells[J]. Journal of Wuhan University of Science and Engineering，2005，18(8)：5-8.

[3] 徐鹏微，杜珂，刘飞，等. 光伏电池阵列模拟器研究[J]. 通信电源技术，2006，23(5)：5-8.

XU Pengwei，DU Ke，LIU Fei，et al. Research on PV Array Simulator[J]. Telecom Power Technologies，2006，23(5)：5-8.

[4] 杜慧. 太阳能发电控制系统的研究[D]. 北京：华北电力大学，2008.

[5] 何国庆，许晓艳，黄越辉，等.大规模光伏电站控制策略对孤立电网稳定性的影响[J]. 电网技术，2009，33(15)：20-25.

HE Guoqing，XU Xiaoyan，HUANG Yuehui，et al. Impact on Stability of Isolated Grid of Different Control Strategies of Large Photovoltaic Station[J]. Power System Technology，2009，33(15)：20-25.

[6] 肖鑫鑫，刘东.分布式供能系统接入电网模型研究综述[J]. 华东电力，2008，36(2)：76-81.

XIAO Xinxin，LIU Dong. Review of Grid-connection Models of Distributed Energy Supply System[J]. East China Electric Power，36(2)：76-81.

[7] 崔开涌，陈国呈，张翼，等.光伏系统最大功率点直接电流跟踪策略[J]. 电力电子技术，2008，42(9)：27-28.

CUI Kaiyong，CHEN Guocheng，ZHANG Yi，et al. A Maximum Power Point Direct Current Tracking Strategy of Photovoltaic System[J]. Power Electronics，2008，42(9)：27-28.

[8] 王夏楠.独立光伏发电系统及其MPPT的研究[D]. 南京：南京航空航天大学，2008.

[9] 廖志凌，阮新波.任意光强和温度下的硅太阳电池非线性工程简化数学模型[J]. 太阳能学报，2009，30(4)：430-435.

LIAO Zhiling，RUAN Xinbo. Non-linear Engineering Simplification Model of Silicon Solar Cells in Arbitrary Solar Radiation and Temperature[J]. ACTA Energiae Solaris Sinica，2009，30(4)：430-435.

[10] 焦阳，宋强，刘文华. 光伏电池实用仿真模型及光伏发电系统仿真[J]. 电网技术，2010，34(11)：198-202.

JIAO Yang，SONG Qiang，LIU Wenhua. Practical Simulation Model of Photovoltaic Cells in Photovoltaic Generation System and Simulation[J]. Power System Technology，2010，34(11)：198-202.

[11] 尚德太阳能电力有限公司. 260 W多晶硅太阳能组件STP260-24/Vd数据手册[EB/OL]. (2010-08-01)[2016-01-18]. https://www.emarineinc.com/pdf/Suntech/SOS80260. pdf.

[12] 刘邦银，段善旭，刘飞，等.基于改进扰动观察法的光伏阵列最大功率点跟踪[J]. 电工技术学报，2009，24(6)：91-94.

LIU Bangyin，DUAN Shanxu，LIU Fei，et al. Photovoltaic Array Maximum Power Point Tracking Based on Improved Perturbation and Observation Method[J]. Transactions of China Electrotechnical Society，2009，24(6)：91-94.

陈杏灿(1990)，男，广东汕头人。在读硕士研究生，主要研究方向为电力系统综合自动化。

程汉湘(1957)，男，湖北武汉人。教授，工学博士，主要研究方向为电力系统综合自动化。

彭湃(1989)，男，湖北天门人。在读硕士研究生，主要研究方向为电力系统综合自动化。

(编辑彭艳)

Modeling of Photovoltaic Cell and Simulation on Photovoltaic Power Generation System

CHEN Xingcan, CHENG Hanxiang, PENG Pai, YANG Jian

(Faculty of Automation, Guangdong University of Technology, Guangzhou, Guangdong 511400, China)

Abstract：Mathematical model of photovoltaic cell and corrected parameters are used to get performance parameters under different environment, simulation model of photovoltaic cell is established in MATLAB/Simulink environment as well, and output characteristics of photovoltaic cell under different illumination intensities and environmental temperatures are analyzed and compared. This paper carries on simulating analysis on arbitrary photovoltaic power generation systems under different illumination intensities and environmental temperatures based on incremental conductance algorithm and boost circuit. Simulation results indicate that this model is able to realize maximum power point tracking of the photovoltaic power generation system and verifies it could satisfy simulation requirements of the photovoltaic power generation system.

Key words：photovoltaic cell; photovoltaic power generation system; MATLAB/Simulink; maximum power point tracking

作者简介：

中图分类号：TM914.4

文献标志码：A

文章编号：1007-290X(2016)02-0025-05

doi:10.3969/j.issn.1007-290X.2016.02.005

收稿日期：2015-08-05修回日期：2015-10-15