基于直接反馈线性化的永磁直驱风力发电系统

童克诚, 孙赟

(国网上海浦东供电公司， 上海 200122)



基于直接反馈线性化的永磁直驱风力发电系统

童克诚, 孙赟

(国网上海浦东供电公司， 上海 200122)

摘要：针对永磁同步发电机(permanent magnet synchronous generator, PMSG)，以额定风速以下风能最大捕获为目标，采用直接反馈线性化理论设计的风力发电控制系统，在电力系统计算机辅助设计和电磁暂态模拟程序软件(power system computer aided design and electric magnetic transient in DC system, PSCAD/EMTDC)仿真平台上建立PMSG风力发电机组模型并进行仿真分析，仿真结果表明，直接反馈线性化方法能够有效实现风力发电机组的最大风能捕获和整个系统的稳定运行，具有较强的鲁棒性。

关键词：永磁同步发电机；风力发电系统；直接反馈线性化；线性控制

随着能源枯竭、环境问题的日益加剧，世界各国正努力寻求多样化的能源供应形式以应对能源危机[1]，风电作为一种重要的可再生能源，具有清洁环保、资源丰富等优点，发展前景好。

与其他风力发电装机类型相比，永磁直驱风力发电系统省去了风力机与发电机之间的升速齿轮箱，大大提高了风机的整体可靠性和效率[2-3]，且随着近年发电机制造技术和永磁制造技术的发展，越来越受到重视。

永磁直驱风力发电系统多采用传统的比例-积分(proportional integral,PI)控制来实现最大功率跟踪控制或者低电压穿越控制[4-7]，但调节参数多，控制器较复杂。不同于PI控制，基于反馈线性化的控制方法可以通过坐标变换和状态反馈，把非线性系统化为线性系统，文献[8]对异步发电机的反馈线性化控制进行了研究，并取得了良好的控制效果；文献[9]采用反馈线性化结合最优跟踪控制方法设计了永磁同步发电机(permanent magnet synchronous generator, PMSG)风力发电控制系统，实现机组的最大风能捕获。直接反馈线性化是基于系统输入-输出描述的一种反馈线性化方法，它能够有效解决多种非线性控制问题。文献[10]利用直接反馈线性化方法对异步发电机的控制进行了研究，并取得了良好的控制效果；文献[11]利用直接反馈线性化理论实现了永磁同步发电机的速度跟踪控制。

本文应用直接反馈线性化的思想，对永磁直驱风力发电系统机侧和网侧换流器进行了控制器的设计，并通过电力系统计算机辅助设计和电磁暂态模拟程序软件(power system computer aided design and electric magnetic transient in DC system, PSCAD/EMTDC)仿真平台搭建PMSG风力发电系统仿真模型，并仿真验证了控制方法的有效性。

1永磁直驱风力发电机组建模

永磁直驱风力发电机组主要由风力机、传动机构、永磁同步发电机、全功率变流器和电网组成。风力机将捕获的风能转化成机械能，并通过传动结构带动永磁同步发电机的转子转动产生电能，经过全功率变流器将其转换成与电网幅值、相位、频率一致的交流电后再经变压器送至电网。永磁直驱风力发电机系统基本结构如图1所示。

图1　永磁直驱风力发电系统基本结构

1.1风力机模型

根据空气动力学原理可知，风力机输出的机械功率

(1)

式中:ρ为空气密度；r为风轮半径；v为风速；CP(λ, β)为风能利用系数；θ为桨距角；λ为叶尖速比，λ=ωr/v；ω为风轮角速度。

由式(1)可知，当风轮半径r一定时，要使风力发电机在某一风速下获得最大机械功率，必须调节CP至最大值。对于三叶片水平轴风轮机，风能利用系数CP的近似数学表达式为

(2)

其中γ=1/[(1/λ+0.08θ)-0.035/(θ3+1)].

当风速在额定值以下时，桨距角θ一般固定为0°，此时，风能利用系数CP与叶尖速比λ的关系曲线如图2所示。

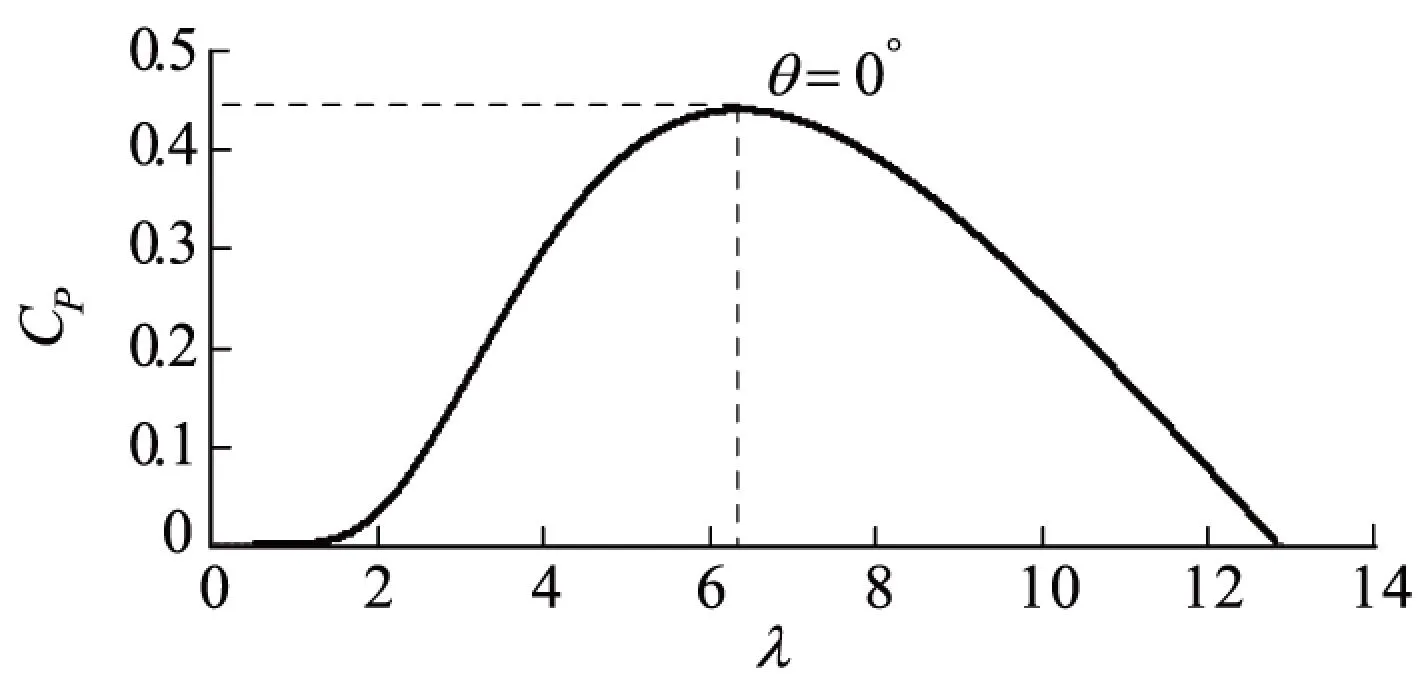
图2　风能利用系数CP的运行曲线

从图2可以看出，当θ一定时，CP只与λ有关，有且只有一个λ使CP取得最大值，称为最佳叶尖速比λopt，对应的风能利用系数为CPmax；因此，要想使风力机获得最大的机械功率，必须使风力机运行于最佳叶尖速比，而由ω=λv/r可知，若要使风力机运行于最佳叶尖速比，则必须根据风速的变化适时调节风力机的转速，以实现风能的最大捕获。

1.2传动系统模型

传动机构模型即轴系模型，有单质块、两质块、三质块和六质块4种[12]。本文忽略内部详细的动态过程，只考虑机械转矩和电磁转矩的相互作用关系，建立单质块模型。在单质块模型中，所有驱动链上的部件被集中为单一的旋转质量，简化后的轴系传动模型可以表示为

(3)

式中:ωg为发电机的转速，由于没有齿轮箱，发电机转速与风力机转速相同，ωg=ω；Tw为风力机的机械转矩；Tex为发电机的电磁转矩；Bm为摩擦系数；Jeq为系统的等效转动惯量。

1.3PMSG模型

在分析永磁同步发电机的基本电磁关系时，假定永磁同步发电机为理想发电机，即满足：

a) 磁饱和效应和涡流损耗可忽略不计；

b) 转子上没有阻尼绕组；

c) 永磁材料的电导率为零；

d) 定子三相对称，感应电动势为正弦。

则同步旋转坐标系下的PMSG的数学模型为：

(4)

式中：ud、uq为发电机定子电压的d、q轴分量；id、iq为定子电流的d、q轴分量；ωr为转子旋转角速度，ωr=pωg，p为发电机极对数；Ld、Lq为d、q轴的定子电感，由于一般不考虑转子磁场的凸极效应且认为发电机气隙均匀，则Ld=Lq=L；Ψf为永磁体的磁链。

永磁同步发电机的电磁转矩

(5)

2PMSG反馈线性化控制

由于永磁直驱发电机是一个复杂强耦合的非线性系统，因此，将其进行线性化解耦会大大提高控制性能。反馈线性化的非线性控制方法可以通过坐标变化和状态反馈，将某些非线性耦合系统线性化并解耦。

根据非线性系统反馈线性化理论，选取状态变量x=[x1,x2]=[id,iq],选取输入变量u=[u1,u2]=[Sd,Sq],输出变量h1[x(t)]=id,h2[x(t)]=iq,则可以将(4)式写成如下形式：

(6)

由式(6)可知，d、q轴电流除受Sd、Sq的控制外，两相电流之间又相互耦合，因此需要找到一种能消除d、q轴之间电流耦合的线性控制方法，现将式(6)表示成：

(7)

为了提高电流控制性能，可采用输入、输出反馈线性化控制思想，引入一组新的输入变量xd、xq来表示，且满足如下的关系式：

(8)

将式(8)代入式(7)，得

(9)

由式(9)可以求得输入变量u=[u1,u2]=[Sd,Sq]的值，即

(10)

由式(10)可知，通过引入新的输入变量xd、xq和电压耦合补偿项ωrid、ωriq，不仅使电流id、iq与新变量xd、xq之间呈线性关系，而且实现了非线性方程的解耦。根据式(10)可以得到永磁同步发电机机侧变流器反馈线性化解耦控制结构如图3所示。

图3　机侧变流器反馈线性化解耦控制系统

同理得到网侧变流器控制结构如图4所示。

图4　网侧变流器反馈线性化解耦控制系统

3仿真分析

为了验证基于直接反馈线性化的PMSG控制策略的有效性，在PSCAD/EMTDC仿真平台上搭建了1.5 MW永磁直驱风力发电系统仿真模型，风力机与永磁同步发电机参数见表1。

表1风力机与永磁同步发电机的参数

风力机永磁同步发电机内容数值内容数值额定功率/MW1.5额定容量/MW1.5叶片半径/m38.5额定电压/kV0.69额定转速/(rad·s-1)2.094额定频率/Hz20额定风速/(m·s-1)10.8定子电阻/Ω0.005空气密度/(kg·m-3)1.225d轴定子电感/mH2转动惯量/(kg·m-2)16000q轴定子电感/mH2最大风能利用系数0.417摩擦系数0.002最佳叶尖速比7.5永磁体磁链/Wb5.476

仿真模型中，直流侧电压设定值udc, ref=1.2 kV；直流侧电容C=50 mF；网侧交流电感Ls=0.5 mH, λ1=10,λ2=20，并考虑以下两种情况：

a) 模拟风速变化(暂时不考虑风速的湍流分量)，即t=2 s时，风速从8 m/s经1 s的时间渐变为10 m/s，之后风速保持不变，仿真结果如图5所示。

图5　风速变化时仿真结果

从图5的仿真结果可以看出，当风速在额定风速以下时，基于直接反馈线性化的PMSG控制器不仅能够有效实现风电机组风能的最大捕获，而且当风速发生渐变时，系统快速响应，实现平稳跟踪，具有较强的鲁棒性。

b) 模拟网侧短路故障，即t=2 s时，网侧发生单相接地短路故障，0.5 s后故障切除，仿真结果如图6所示。

图6　网侧单相接地故障时的仿真结果

从图6的仿真结果可知，当网侧发生单相接地故障时，所设计的控制器使系统能够顺利实现故障穿越，且网侧故障对机侧系统影响很小，提高了整个系统的可靠性。

4结论

本文利用反馈线性化理论设计了永磁直驱风力发电系统机侧和网侧控制器，并利用PSCAD/EMTDC仿真平台进行了仿真，仿真结果表明，永磁直驱风力发电系统采用直接反馈线性化控制时不仅减少了PI参数调节，简化了控制器，且具有良好的动态响应性能。

参考文献：

[1] 雷亚洲，GORDON L.风力发电与电力市场[J]. 电力系统自动化，2005,29(10): 1-5.

LEI Yazhou, GORDON L. Wind Power Generation and Electricity Market[J]. Automation of Electric Power Systems, 2005,29(10): 1-5.

[2] ABBEY C, JOOS G. Effect of Low Voltage Ride Through (LVRT) Characteristic on Voltage Stability[C]// IEEE Power Engineering Society General Meeting. SanFrancisco, USA: IEEE, 2005(2): 1901-1907.

[3] 田迅, 任腊春. 风电机组选型分析[J]. 电网与清洁能源, 2008, 24(4):36-39.

TIAN Xun, REN Lachun. Selection of Wind Turbines[J]. Power System and Clean Energy, 2008, 24(4):36-39.

[4] 严干贵, 魏治成, 穆钢, 等. 直驱永磁同步风电机组的最优功率运行控制[J]. 电机与控制学报, 2009, 13(1): 56-61.

YAN Gangui, WEI Zhicheng, MU Gang, et al. Optimal Power Control of Directly-driven Permanent Magnet Synchronous Wind Turbine [J]. Electric Machines and Control, 2009, 13(1): 56-61.

[5] LI Shuhui, TIMOTHY A, XU Ling. Conventional and Novel Control Designs for Direct Driven PMSG Wind Turbines[J]. Electric Power Systems Research, 2010:80(3) 328-338.

[6] 姚骏, 廖勇, 瞿兴鸿，等. 直驱永磁同步风力发电机的最佳风能跟踪控制[J]. 电网技术, 2008, 32(10):11-15.

YAO Jun, LIAO Yong, QU Xinghong, et al. Optimal Wind-Energy Tracking Control of Direct-driven Permanent Magnet Synchronous Generators for Wind Turbines [J]. Power System Technology, 2008, 32(10):11-15.

[7] 赵兴勇. 直驱永磁同步风力发电机组低电压穿越控制策略[J]. 中国电力, 2011, 44(5):74-77.

ZHAO Xingyong. LVRT Control Strategy of Directly-driven Permanent Magnet Synchronous Wind Turbine [J]. Electric Power, 2011, 44(5):74-77.

[8] 张纯明, 郭庆鼎. 基于反馈线性化的交流直线永磁同步伺服电动机速度跟踪控制[J]. 电工技术学报，2003，18(3):5-9.

ZHANG Chunming, GUO Qingding. Feedback-linearization Based Control of Speed Tracking for AC Linear Permament Magnet Synchronous Servo Motor [J]. Transaction of China Electrotechnical Society，2003，18(3):5-9.

[9] 王伟，陈奇，纪志成. 基于反馈线性化PMSG风力发电系统控制[J]. 系统仿真学报，2010, 22(6):1397-1401.

WANG Wei, CHEN Qi, JI Zhicheng. Feedback Linearization Control of PMSG-based Wind Power Generation System [J]. Journal of System Simulation, 2010,22(6):1397-1401.

[10] 张春朋，林飞.基于直接反馈线性化的异步电动机非线性控制[J]. 中国电机工程学报, 2003,23(2): 99-102.

ZHANG Chunpeng, LIN Fei. Nonlinear Control of Induction Motors Based on Direct Feedback Linearization [J]. Proceedings of the CSEE, 2003, 23(2): 99-102.

[11] 刘栋良,赵光宙. 基于直接反馈线性化的永磁同步机速度跟踪控制[J]. 电气自动化，2006, 28(2):81-84.

LIU Dongliang, ZHAO Guangzhou. Speed Tracking Control of PMSM Based on Direct Feedback Linearization[J]. Electric Automation, 2006, 28(2):81-84.

[12] MUYEEN S M，TAMURA J, MURATA T.风电场并网稳定性技术[M]. 北京：机械工业出版社，2011.

童克诚(1982)，男，上海市人。工程师，工学硕士，从事新能源并网技术工作。

孙赟(1990)，男，上海市人。助理工程师，工学学士，从事新能源并网技术工作。

(编辑王夏慧)

Permanent Magnet Direct-driven Wind Power Generation System Based on Direct Feedback Linearization

TONG Kecheng, SUN Yun

(State Grid Shanghai Pudong Electric Power Supply Company, Shanghai 200122, China)

Abstract：Taking maximum wind energy capture below rated wind speed as a target, this paper uses direct feedback linearization theory to design wind power generation control system based on permanent magnetic synchronous generator (PMSG). On the simulation platform called power system computer aided design and electric magnetic transient in DC system (PSCAD/EMTDC), it establishes PMSG wind power generation unit model and carries out simulation analysis. Results indicate that the method of direct feedback linearization could effectively realize maximum wind energy capture of wind power generation unit and stable operation of the whole system which has stronger robustness.

Key words：permanent magnetic synchronous generator; wind power generation system; direct feedback linearization; linear control

作者简介：

中图分类号：TM614

文献标志码:A

文章编号：1007-290X(2016)02-0021-04

doi:10.3969/j.issn.1007-290X.2016.02.004

收稿日期：2015-11-17