基于可靠度的风电机组机会维修策略

张琛，郭盛，高伟，邱逢涛，杨涛,李友良

(1.华中科技大学 能源与动力工程学院，湖北 武汉430074；2.华能湖北分公司，湖北 武汉430077)



基于可靠度的风电机组机会维修策略

张琛1，郭盛1，高伟1，邱逢涛2，杨涛1,李友良1

(1.华中科技大学 能源与动力工程学院，湖北 武汉430074；2.华能湖北分公司，湖北 武汉430077)

摘要：在传统预防性维修的基础上，提出基于可靠度的风电机组机会维修策略，当某一部件损坏造成系统必须停机维修时，可将其他未发生故障部件的维修时刻提前，从而减少系统停机次数。结合具体风力机实例，通过仿真分析验证了机会维修策略相较于传统预防性维修策略的经济性优势,并结合果蝇算法求出最佳机会维修阈值。

关键词：风力机；可靠度；机会维修；果蝇算法

随着风力机空气动力学、叶片叶形设计、故障诊断等技术的突破，风力发电产业正得到迅猛的发展。全球风能理事协会发布的最新数据显示，2014年全球风电新增装机容量51.477 GW，累计装机容量达369.553 GW[1]。根据丹麦BTM公司的预测，在接下来的5年时间内，全球风能的累计装机容量将以平均每年12%的速度递增。由于风力机大部分运行在风沙、潮湿、腐蚀等恶劣环境下，随着装机容量的递增，风电场的故障概率呈现上升的趋势。有文章指出，陆上风力发电机组每千瓦时的运行检修费用占总生产成本的15%～20%，而海上风电机组的维修费用则更高[2]。所以，针对风电场的实际运行状况，选择科学、合理的维修策略势在必行。

传统的维修策略大致可以分为3类：事后维修、预防维修、状态维修。事后维修主要是针对小型系统，故障的发生对于产品或环境的影响不大时采取该维修方式。预防维修是在故障还没发生之前，按照事先预定的时间间隔所采取的维修措施。状态维修是根据系统的实时状态数据来调整维修计划，是一种更为精确的维修方式，但是系统需要配备复杂、昂贵的状态监测、数据处理、维修决策设备，成本较高。机会维修策略是在预防维修的基础上发展起来的维修方式，它利用了系统部件之间的相关性。对于电力系统，部件的故障维修必然伴随着巨大的停机损失，机会维修策略就是利用系统的停机时刻，对系统其他满足预设条件的部件进行提前维修，从而达到节省维修成本的目的。

机会维修策略是近年来维修领域的研究重点，在国内外已取得不少的研究成果。赵洪山等[2-3]提出了机会更换概率密度的近似分布函数，并在分别考虑随机故障和不考虑随机故障的前提下，通过寻优算法得出风力机各部件的最佳维修阈值；蔡景等[4-5]利用蒙特卡洛仿真方法，给出系统随机故障的产生时刻，通过系统维修成本率和可用度验证了机会维修的实践意义。杨元等[6]提出了从时间相关性、故障相关性、结构相关性和功能相关性4个方面描述多部件系统的维修相关性，并建立多部件系统机会成组优化模型，得到各部件的最佳机会维修阈值集。Fard等[7]针对K类部件预设了维修阈值L和维修冗余u，在对达到L的部件进行维修的同时，对处于(L-u，L)的其他未故障部件同样实施维修，以维修成本率作为决策目标，寻求最佳L和u值。Pham等[8]以k-out-of-n的表决系统为研究对象，建立其机会型预防维修模型。Ding等[9]在考虑不完全维修影响的前提下，给出3种预防维修策略，并以实例说明机会维修策略的可行性。

现有的机会维修策略大多以时间条件作为维修的阈值，而且对最佳维修阈值的讨论较少。由于在实际的风力机运行过程中，设备的状态与运行时间之间并非单纯的线性关系，仅仅以时间作为维修条件会导致维修策略的实施与系统运行状态不同步，无法满足生产实际需求。本文在总结前人工作的基础上，提出以可靠度作为维修决策阈值，针对具体的风力机实例，通过仿真算法验证机会维修的可行性，并结合果蝇寻优算法提出风力发电系统的最优机会维修阈值，为实际的运行维修提供指导。

1风力机组机会维修策略

1.1可靠度理论

可靠度是指部件在特定的时间和环境下完成规定功能的概率。对于一个全新的部件，其可靠度为1；对于完全失效、丧失工作能力的部件，其可靠度为0。所以，随着部件的运行，其可靠度函数是从1到0的递减函数。根据风力机的故障统计数据，两参数的威布尔分布可以近似表达出其可靠度的变化过程。部件i的可靠度函数

式中：αi为部件i的尺度参数，其值影响着威布尔函数曲线尺寸比例的大小；βi为部件i的形状参数，其值影响着曲线的形状；t为时间。

通过风电机组各关键部件的失效函数h(t)及其历史故障数据，利用最大似然估计方法可求取αi和βi。产品的失效率表示产品裂化过程中丧失工作能力的概率。对于满足两部件威布尔分布的部件i而言，其失效率函数

1.2随机故障时间的产生

产生一组(0,1)内的均匀随机数δ1，δ2，…，则部件i的随机故障时刻

1.3模型假设

为较好地说明情况和简化计算，本文的维修模型基于以下假设：

a)风力机各部件服从威布尔分布，且故障率分布相互独立。

b)风力机任一部件的故障会导致系统故障，且必须停机维修，停机维修时间相对于系统的运行时间可忽略不计。

c)只考虑风力机各部件之间的经济相关性影响，不考虑结构相关、故障相关等其他相关性。

d)在风力机维修成本中，考虑系统固定维修费用(即系统停机损失)、故障维修费用、预防维修费用，且故障维修费用远远大于预防维修费用。

1.4机会维修模型

传统的预防性维修不考虑部件之间的相关性，每个部件按照其单独设定的维修计划进行维修，当任一部件发生随机故障，或达到其预防维修阈值时，系统即停机对部件进行更换维修。而机会维修则充分利用部件之间的相关性，当某一部件的损坏造成系统必须停机进行维修，其他尚未故障的部件即获得一个维修机会，这时可以考虑将未发生故障部件的维修时刻提前，利用系统巨大的停机损失来达到节约成本的目的。

基于可靠度的机会维修策略如图1所示，其中Ro为预设机会维修可靠度阈值，Rp为预设预防维修可靠度阈值，to为机会维修时刻，tp为预防维修时刻。

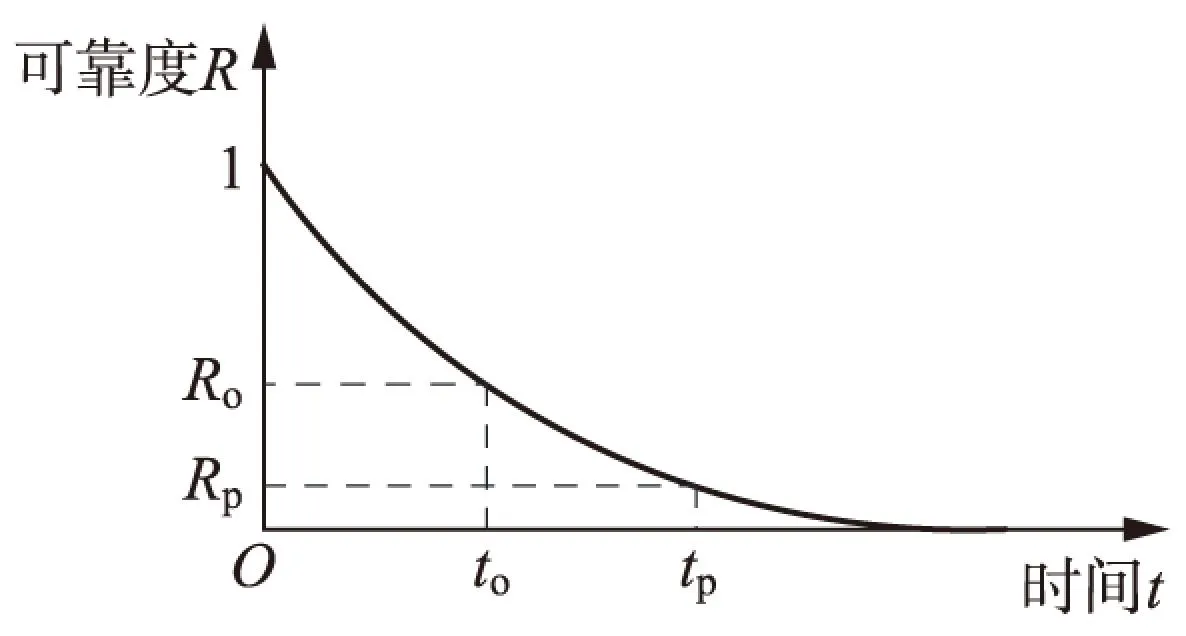
图1　机会维修策略

预先设定各部件的机会维修可靠度阈值和预防性维修可靠度阈值，当部件运行在0～to时间段，发生随机故障时，系统即停机进行更换；当部件运行至to～tp时间段，发生故障即停机更换，或者有其他部件故障导致系统停机时进行机会维修；当部件运行至tp时则进行预防性更换。

2数值计算

风力机系统的预防维修策略、机会维修策略流程分别如图2、图3所示，其中tpj为部件j的预防维修时刻，tfj为部件j的故障维修时刻，toj为部件j的机会维修时刻，pi和fi分别为部件i的预防维修次数和故障维修次数，oj为部件j的机会维修次数，n为预先设定的仿真次数。

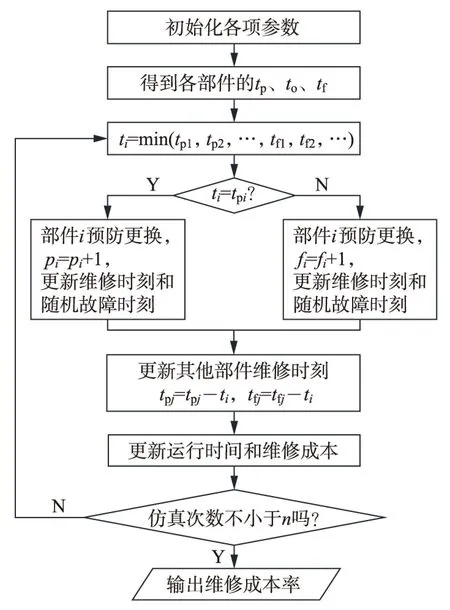
图2　预防维修策略流程

图3　机会维修策略流程

通过记录各部件在预设仿真次数下的维修次数，可得到系统的维修成本率η，其计算式为

式中：C0为系统的固定维修费用，Cfi为部件i的故障维修费用，Cpi为部件i的预防维修费用，Coi为部件i的机会维修费用，T为系统运行总时间。

3算例分析

3.1仿真分析结构比较

本文结合文献[9]算例对所提仿真算法进行验证，将风力发电系统简化为由转子、轴承、齿轮箱和发电机4部件组成的系统，各部件的威布尔分布参数以及维修数据见表1。为了简化计算，本文设置4部件的预防维修可靠度阈值均为0.1，机会维修可靠度均为0.2。

表1风力机各部件威布尔参数

部件威尔布参数αi/dβi维修费用/万元C0CfiCpiCoi转子300033.511.22.82.8轴承375023.56.01.51.5齿轮箱240033.515.23.83.8发电机330023.51.02.52.5

预设总的仿真次数为10 000次，每次仿真系统均产生新的随机数，可认为这10 000次仿真独立同分布，可适用于经典统计分析方法[5]。预防性维修与机会维修仿真结果比较见表2。

表2仿真结果比较

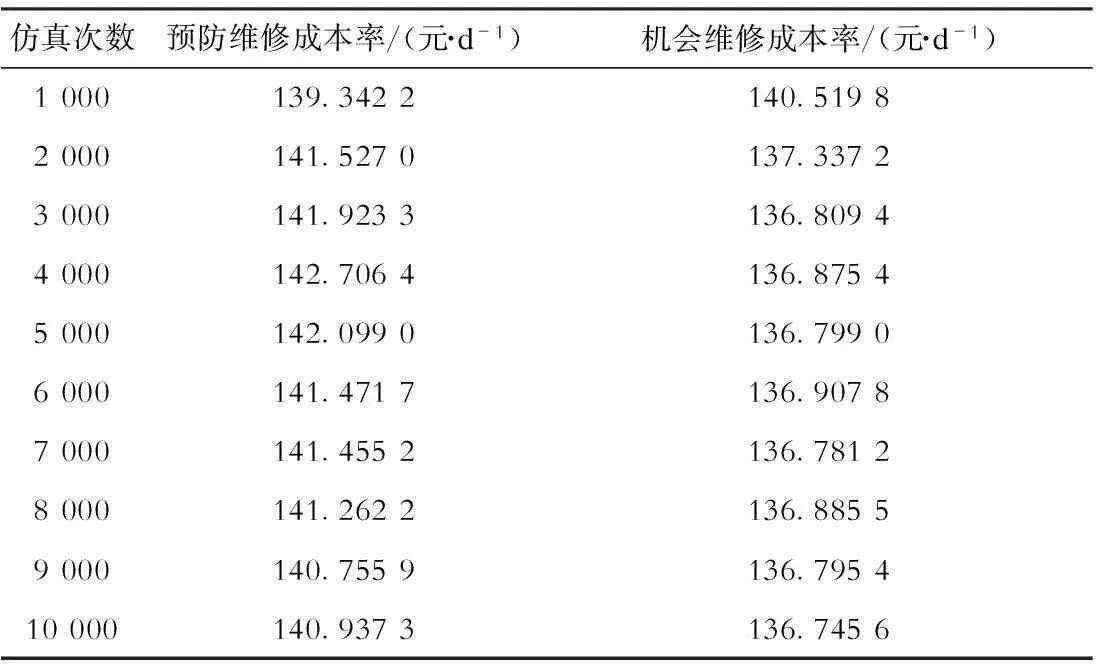
仿真次数预防维修成本率/(元·d-1)机会维修成本率/(元·d-1)1000139.3422140.51982000141.5270137.33723000141.9233136.80944000142.7064136.87545000142.0990136.79906000141.4717136.90787000141.4552136.78128000141.2622136.88559000140.7559136.795410000140.9373136.7456

由表2可看出：随着仿真次数的逐步增加，维修成本率的计算结果也逐渐稳定；与传统的预防维修相比，机会维修成本的经济性优越。

3.2最优机会维修阈值

果蝇优化算法是由中国台湾学者潘文超于2011年6月提出的，用于金融预警模型的研究，是一种基于果蝇觅食行为推演出寻求全局优化的新方法，是在粒子群等群智能算法的基础上发展而来的。依据果蝇的基本生理特性，将其寻找食物的过程进行仿真模拟，从而获得具有良好全局性能的寻优方法。其本身具有寻优速度快、不易陷入局部最优、稳定性高、寻优精度高等特点，其应用领域相当广泛，特别是在函数优化、神经网络、支持向量回归参数优化、财务管理、企业风险预警方面有着重要的应用价值[10-11]。基于果蝇寻优算法，针对上文风力机实例的简化模型，寻求风力发电系统的最佳机会维修阈值。

在实际运行维护过程中，部件的预防维修阈值一般根据材料特性和历史参数提前设定，所以在寻优过程中仍然假定风力机4部件的预防维修可靠度阈值为0.1。果蝇算法仿真寻优过程如图4所示。

图4　果蝇算法迭代寻优过程

由图4可得：随着迭代次数的逐渐增加，系统机会维修成本率为101.278 8 元/天，此时对应的机会维修可靠度阈值为0.801 1，即当系统必须停机维修时，对可靠度达到0.801 1的未故障部件实施提前更换维修，系统的维修成本率达到最小值。

4总结

机会维修策略是在传统预防性维修策略的基础上发展起来的，在风电场维修策略的研究与应用中受到越来越多的关注。机会维修的一大优点就是可以利用系统庞大的停机损失，而这一优势在风电场特别是海上电场可以得到放大。

本文首先介绍了基于可靠度的机会维修策略模型，并与传统的预防维修模型相比较。结合具体的算例，以维修成本率作为决策目标，仿真结果显示与预防维修策略相比，机会维修在经济性方面体现出优势。最后结合果蝇寻优算法求取风力系统的最佳机会维修阈值，对实际的运行维护有一定的指导意义。

参考文献：

[1] 全球风能理事会. 2014年全球风电装机容量统计[J]. 风能，2015(2)：50-53.

GWEC. 2014 Global Wind Power Installed Capacity Statistics[J]. Wind Energy, 2015(2):50-53.

[2] 赵洪山,鄢盛腾,张小田.风电机组确定性机会更换维修策略的研究[J]. 太阳能学报,2014,35(4):568-574.

ZHAO Hongshan, YAN Shengten, ZHANG Xiaotian. Deterministic Opportunistic Replacement Maintenance Strategy for Wind Turbine[J]. Acta Energiae Solarris Sinica, 2014, 35 (4): 568-574.

[3] 赵洪山,张路朋. 基于可靠度的风电机组预防性机会维修策略[J]. 中国电机工程学报,2014, 34(22): 3777-3782.

ZHAO Hongshan, ZHANG Lupeng. Preventive Opportunistic Maintenance Strategy for Wind Turbines Based on Reliability[J]. Proceedings of the CSEE, 2014 , 34 (22) : 3777-3782.

[4] 赵洪山,鄢盛腾,刘景青.基于机会维修模型的风电机组优化维修[J]. 电网与清洁能源,2012,28(7):1-5.

ZHAO Hongshan, YAN Shengteng, LIU Jingqing. Optimization Maintenance of Wind Turbine Based on Opportunisticmaintenance Model[J]. Power System and Clean Energy, 2012, 28(7): 1-5.

[5] 肖罗椿,蔡景,李鑫.系统单个部件机会维修的费用和可用度仿真[J]. 四川兵工学报,2014,35(6):40-43.

XIAO Luochun, CAI Jing, LI Xin. System Maintenance Cost and Availability Simulation Based on Single-part Opportunistic Maintenance[J]. Journal of Sichuan Ordnance, 2014, 35(6): 40-43.

[6] 杨元,黎放,侯重远,等.基于相关性的多部件系统机会成组维修优化[J]. 计算机集成制造系统，2012,18(4):827-832.

YANG Yuan, LI Fang, HOU Zhongyuan,et al. Opportunistic Group Maintenance Optimization of Multi-unit System Under Dependence[J]. Computer Integrated Manufacturing Systems, 2012, 18(4): 827-832.

[7] ZHENG X, FARD N. A Maintenance Policy of Deteriorating Systems[J]. European Journal of Operational Research, 2002 (139): 469-489.

[8] PHAM H, WANG H. Optimal(τ,T) Opportunistic Maintenance of ak-out-of-n:G System with Imperfect PM and Partial Failure[J]. Naval Research Logistics, 1996 (47): 223-239.

[9] DING F F, TIAN Z G. Opportunistic Maintenance for Wind Farms Considering Multi-level Imperfect Maintenance Thresholds[J]. Renewable Energy, 2012 (45): 175-182.

[10] 胡能发.演化式果蝇算法及其应用研究[J]. 计算机技术与发展,2013,23(7):131-134.

HU Nengfa. Evolutionary Fruit Algorithm and Its Application Research[J]. Computer Technology and Development, 2013, 23(7): 131-134.

[11] 祁丽婉,梁庚,童国炜.基于果蝇算法优化BP神经网络的齿轮箱故障诊断[J]. 电网与清洁能源,2014,30(9):31-36.

QI Liwan. LIANG Geng, TONG Guowei. A Gear Box Fault Diagnosis Method Based on Fruit Fly Optimization Algorithm to Optimize the BP Neural Network[J]. Power System and Clean Energy, 2014, 30(9):31-36.

张琛(1992)，男，湖北鄂州人。在读硕士研究生，研究方向为风电场智能化运行维修策略。

郭盛(1992)，男，河南漯河人。在读博士研究生，研究方向为振动信号处理及故障诊断。

高伟(1954)，男，湖北汉川人。教授，工学博士，从事热工过程自动化、热力设备与系统动态特性分析、辨识与建模、数字仿真研究工作。

(编辑李丽娟)

Opportunistic Maintenance Strategy for Wind Power Generators Based on Reliability

ZHANG Chen1, GUO Sheng1, GAO Wei1, QIU Fengtao2, YANG Tao1, LI Youliang1

(1.The School of Energy and Power Engineering, Huazhong University of Science and Technology, Wuhan, Hubei 430074, China; 2.Huaneng Hubei Branch, Wuhan, Hubei 430077, China)

Abstract：On the basis of traditional preventable maintenance, an opportunistic maintenance strategy for wind power generators based on reliability is proposed, which means that when damage of some component causes necessary shut-down and maintenance, it is able to bring forward maintenance time of other components without failures, so as to reduce shut-down times. It is proved by specific wind turbine examples and simulating analysis that this opportunistic maintenance strategy has better economy advantages compared with traditional preventable maintenance strategy. Optimal opportunistic maintenance threshold could be determined by using fruit fly optimization algorithm.

Key words：wind turbine; reliability; opportunistic maintenance; fruit fly optimization algorith

作者简介：

中图分类号：TM614

文献标志码：A

文章编号：1007-290X(2016)02-0040-05

doi:10.3969/j.issn.1007-290X.2016.02.008

基金项目：国家科技支撑计划资助项目(2015BAA06B02)

收稿日期：2015-10-26