基于EEMD-RVM的短期风功率区间预测

范磊，王越，梁智，戴丽媛

(1.河海大学 能源与电气学院，江苏 南京 210098；2.国家电网常州供电公司，江苏 常州 213000)



基于EEMD-RVM的短期风功率区间预测

范磊1，王越2，梁智1，戴丽媛1

(1.河海大学 能源与电气学院，江苏 南京 210098；2.国家电网常州供电公司，江苏 常州 213000)

摘要：针对现有风功率预测方法多为确定性的点预测，无法描述风功率的随机性的问题，建立了基于集合经验模态分解和相关向量机的短期风功率区间预测模型。首先对原始风功率序列进行集合经验模态分解，获得一个剩余分量及多个具有不同特性的固有模态分量；然后对各分量采用相关向量机算法分别建立区间预测模型；最后将各分量的预测结果进行叠加得到一定置信水平下的区间预测结果。仿真结果表明，所提的区间预测方法具有较高的预测精度和较窄区间宽度，区间覆盖率较高。

关键词：短期风功率预测；区间预测；相关向量机；集合经验模态分解；混合核函数

在化石能源紧缺和环境问题严峻的今天，开发利用清洁无污染的可再生能源已成共识。其中风力发电因其清洁无污染、储量丰富、可循环利用受到越来越多的重视与关注。由于自然风存在一定的随机性和波动性，导致风机发生较大的功率波动，给电网的供需平衡与安全稳定运行造成巨大影响。因此准确的风功率预测是合理制定发电计划与安排系统备用的前提，是提高风电在电网比重的关键[1]。

研究国内外相关文献可以发现，与传统确定性点预测方法相比，目前区间预测仍处于起步阶段。文献[2-3]采用Bootstrap重抽样法构造样本，需要大量处理数据，耗时较长；文献[4-5]通过分位点法描述预测对象的概率信息，需要预先确定回归模型和分位点，模型计算量大；文献[6]提出了以极限学习机的点预测方法为基础，构造比例系数，从而获得短期负荷的区间，但是其最优系数的获取方法有待验证；文献[7-9]采用基于贝叶斯理论的概率预测法，其结果具有概率意义，可得出预测量的期望值及其分布特性，因而可得出任意置信水平下的区间预测结果。

针对上述研究现状，本文重点研究了基于概率的区间预测[10-12]方法，并在此基础上提出一种基于集合经验模态分解和相关向量机的短期风功率区间预测模型。一方面引入集合经验模态分解降低数据的复杂度；另一方面采用局部核-高斯核和全局核-多项式核的组合构成相关向量机的核函数，进一步改善区间预测的效果。运用本文模型对风电场的实测风功率序列进行提前15 min的短期风功率区间预测，并采用多种评价指标对本文模型的预测效果进行评估，结果表明本文模型具有较高的预测精度与较窄的区间宽度，区间预测效果较为理想。

1集合经验模态分解

考虑实际风功率的随机性与波动性，直接对原始风功率序列进行预测的误差较大。本文采用集合经验模态分解方法对原始数据进行分解，以降低数据复杂度。与小波变换、经验模态分解以及其他信息处理方法相比，集合经验模态分解方法克服了小波变换需人为设定、主观性强的不足，避免了经验模态分解易出现模态混叠的问题，具有更高的分辨率与很强的非线性处理能力，更适于处理随机性强的风功率数据[13]。

1.1经验模态分解算法原理

经验模态分解(empirical mode decomposition, EMD)[14]是一种高效的信号分解方法，其将任意信号中不同尺度的波形或趋势逐级分解出来，产生一个剩余分量(residual, RES)以及一系列的特征模态函数分量(intrinsic mode function，IMF)[15]。所有IMF必须满足下列条件：在整个数据序列中，极值点的数量与过零点的数量相等，或相差不能多于一个；在任一点上，信号的局部最大值和局部最小值定义的包络均值为零。

EMD分解流程如下：

a) 初始化循环变量i=1，x1(t)=x(t)，其中x(t)为待分解的原始数据序列。

b) 初始化循环变量j=1，y1(t)=x1(t)。

c) 找出序列yj(t)中所有局部极大值并拟合成包络线uj(t)；同理，找出yj(t)中所有局部极小值并拟合成包络线vj(t)；这2条上下包络线应包络所有的数据点，其上下包络线的平均值

(1)

并计算原始信号与包络均值的差值

(2)

d) 判断hj(t)是否满足IMF的2个条件，若不满足，则j=j+1，yj(t)=hj-1(t)，重复步骤c)；若满足，则可得第i个IMF，即

(3)

则剩余分量

(4)

e) 判断ri(t)是否满足终止条件，若不满足，则xi+1(t)=ri(t)，i=i+1，重复b)至d)，否则分解结束。由此共可分解出n个IMF分量ci(t)和一个剩余分量rn(t)，EMD对x(t)的分解过程结束。

由此原始序列

(5)

1.2集合经验模态分解算法原理

集合经验模态分解(ensemble empirical mode decomposition, EEMD)是Wu和Huang等人为改善EMD方法中模态混叠的缺点，在2005年提出的新型噪声辅助数据分析方法[16]。该方法在EMD的基础上加入了高斯白噪声，并进行多次EMD分解，最后将多次分解的IMF总体平均定义为最终的IMF。由于高斯白噪声具有频率均匀分布的统计特性，所以它可以使信号在不同的尺度上具有连续性，有效避免了EMD分解过程中由于IMF的不连续性而造成的混叠现象，明显改善EMD方法。

EEMD方法中用到的2个重要参数分别是白噪声的幅值k和重复进行EMD分解的总次数M。目前，关于M和k值的确定多基于尝试经验和数据的结构特点，一般M取100，k取0.05～0.5倍为宜。

EEMD方法的具体步骤为：

a) 设定k和M；

b) 原始数据序列中加入高斯白噪声；

c) 按照EMD方法将加入白噪声的数据序列进行分解，得到一系列的IMF分量及RES分量；

d) 重复加入相同幅值的不同白噪声序列，重复b)和c)，对M次EMD分解得到的各个IMF分量及RES分量计算均值，即

(6)

与其他预测算法相比，相关向量机不仅具有相关模型高度稀疏、待优化核参数少、核函数选择灵活、模型泛化能力强的优点，而且能直接实现区间的预测。因此本文采用相关向量机对由EEMD分解得到的分量分别建立模型进行区间预测。

2相关向量机模型

由相关向量机(relevance vector machine，RVM)的原理[18]可知，在进行点预测时，仅使用了预测均值这一个量来表示其确定性的预测结果。而使用RVM实现区间预测时，需同时考虑模型的预测均值和方差。

(7)

式中：w=(w0,w1,…,wN)T为权值向量；样本噪声εi服从N(0，σ2)的高斯分布，则RVM模型可表示为

(8)

式中：K(x,xi)为核函数；x为相关向量；ε为服从N(0，σ2)的独立样本误差。

对于相互独立的输出集t，整个训练样本的似然函数

(9)

式中：Φ=(φ(x1),φ(x2),…,φ(xN))T，φ(xi)=(1，K(x1,xi),K(x2,xi),…,K(xN,xi))T。

(10)

式中：超参数α=(α0,α1,…,αN)T，每个独立的αj都只与其对应的权值wj相关。根据贝叶斯公式，利用样本似然函数式(9)和w先验分布式(10)可以得到w的后验分布计算公式：

(11)

(12)

后验协方差矩阵Σ和均值μ分别为：

(13)

(14)

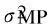
(15)

式(15)服从高斯分布，即

(16)

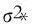
(17)

由式(17)可以看出，RVM模型可以同时得出输入向量对应的预测均值和方差，因此，RVM模型能反映预测数据的不确定性，得到一定置信范围内的区间预测。在给定置信度下，预测结果的置信区间[19]可表示为

(18)

式中：Lb和Ub分别表示预测值的下界和上界；zα/2为正态分布的双侧α分位点。

3基于EEMD-RVM的短期风功率区间预测

3.1使用EEMD对原始风功率序列进行分解

如图1所示，实际风功率具有明显的随机性与波动性。若直接采用预测算法对风功率序列进行预测会存在较大误差。为提高预测精度，需对原始序列进行分解以降低数据复杂度。本文采用EEMD方法对原始风功率序列进行分解，获得若干个不同频率的分量。由以上分量可以更明显地看出原序列的周期性、随机性和趋势性。

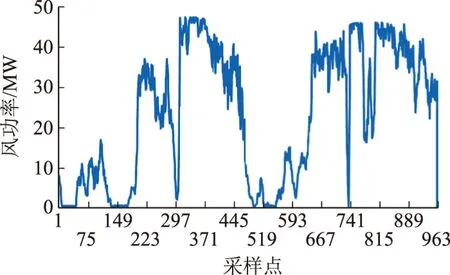
图1　实际风功率序列波动趋势

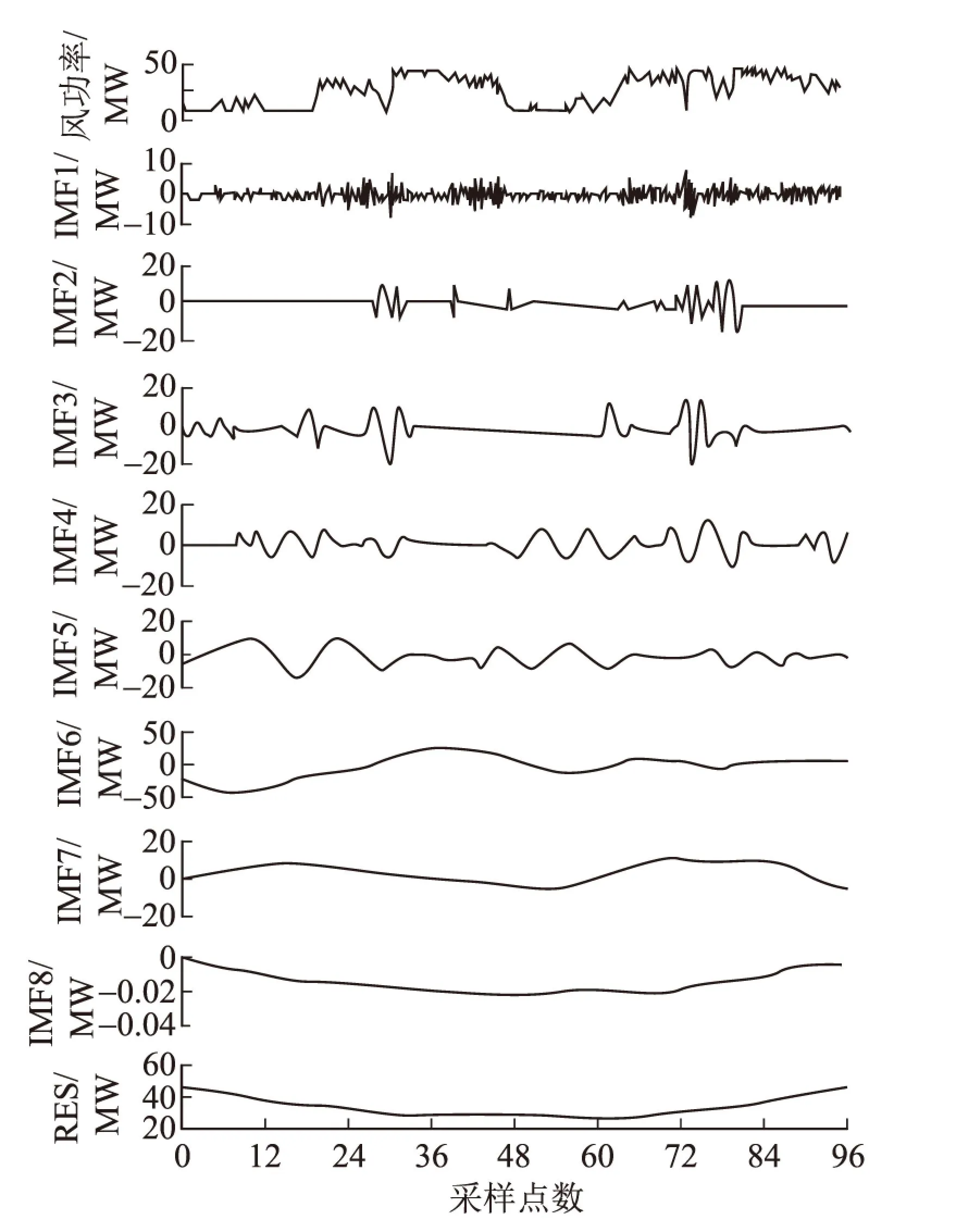
选择国内某一风电场为研究对象，其风机总数为33台，装机容量为49.5 MW。以2009年4月12—22日共960个点的风功率序列为例，EEMD分解效果如图2所示。

3.2RVM模型的参数设定

组合核思想是将多个不同的核函数结合起来，使得组合后的核函数具有更好的特性[18]。考虑到RVM核函数的选取不需满足Mercer条件，核函数的选择较为自由，且径向基核处理局部波动以及多项式核解决全局波动具有优异特性，因此本文将以上2种核函数进行线性组合，构成如下组合核函数：

(19)

(20)

(21)

式中：G(x,xi)为径向基核；P(x,xi)为多项式核；k1为核函数的系数权重，0

本文采用网格搜索法寻找参数k1和δ最优值。

图2　EEMD分解效果示意图

3.3区间预测效果的评价指标

本文采用三项指标，即平均相对误差(mean absolute percentage error，MAPE)[7]、区间覆盖率(forecasting interval coverage percentage，FICP)[6]、区间平均宽度(forecasting interval average width，FIAW)[6]，对区间预测的效果进行评判。

3.3.1MAPE

MAPE的计算如下：

(22)

3.3.2FICP

FICP的计算如下：

(23)

式中:N为预测样本的个数；ξ(1-α)为置信度1-α下实际值落在预测置信区间内的个数。FICP用于评价构建区间的可信程度，其绝对值越大，可信度越高。

3.3.3FIAW

FIAW的计算如下：

(24)

3.4算法流程框图

本文提出了基于集合经验模态分解和相关向量机的短期风功率区间预测模型(EEMD-RVM模型)。首先采用EEMD方法将风功率序列分解成多个IMF分量及RES分量，然后采用组合核RVM模型进行一天96点(间隔15 min)的风功率区间预测，其具体实现步骤如图3所示。

图3　基于EEMD-RVM的短期风功率区间预测模型框图

4算例分析

采用江苏省某风电场2009年全年的风功率序列作为研究对象，以前10天的实测风功率值作为训练样本，对第11天进行提前一点(即提前15 min)的风功率区间预测。

为验证EEMD-RVM模型的区间预测效果，在不同置信水平(本文以90%、70%为例)下实现短期风功率区间预测，区间预测结果如图4、图5所示。采用MAPE、FICP、FIAW指标对区间预测的效果进行评估，部分预测结果见表1，MAPE、FICP和FIAW在90%、70%置信水平下数值分别为4.54%、90.63%、0.911 8，4.54%、71.88%、0.112 2。

图4　90%置信度下的短期风功率区间预测结果

图5　70%置信度下的短期风功率区间预测结果

表1EEMD-RVM模型的区间预测结果

时刻90%置信水平70%置信水平实际风功率/MW预测期望/MW0:00[37.90,44.35][39.24,43.02]40.9641.140:15[38.28,44.73][39.62,43.40]40.2941.520:30[39.41,45.86][40.75,44.53]43.4242.650:45[40.26,46.72][41.61,45.38]43.4743.51……………23:30[22.71,29.16][24.05,27.83]26.2325.9523:45[27.48,33.93][28.82,32.59]31.3830.72

从图4、图5及表1可以看出：本文模型的短期风功率预测期望值能够有效跟随实际值，其上下浮动趋势与实际负荷变化情况基本一致；从图4、图5实际风功率在区间内的分布情况来看，实际风功率大部分都落在置信度为90%和70%的预测区间之内，但实际值落在70%置信度预测区间之外的个数明显比90%的多，情况与实际符合，体现了本文区间预测结果的有效性；90%置信水平的预测区间宽度明显大于70%的预测区间宽度，随着置信度的降低，区间预测的区间宽度降低，区间覆盖率也随之降低。

为了进一步评估本文所提EEMD-RVM模型的区间预测效果，将EEMD-RVM模型分别与标准RVM模型、小波-RVM模型、EMD-RVM模型的预测结果进行对比，并采用MAPE、FICP、FIAW指标以及运行时间t对区间预测的效果进行评价，90%置信水平下的指标评价结果见表2。

表2各预测模型90%置信水平下的指标评价结果

模型类型σMAPE/%k(1-α)FICP/%h(1-α)FIAWt/s标准RVM7.0889.370.283527EMD-RVM4.5490.630.172253小波-RVM5.9489.610.191864EEMD-RVM3.5693.880.150181

由表2各种模型指标结果可以得出以下结论：总体上看，本文模型的预测误差最小，区间宽度最窄，区间覆盖率最高，运行时间虽有所延长，但仍在工程实际要求的范围内，模型的区间预测效果较为理想；与标准RVM模型相比，所有先分解后预测模型的预测误差、区间覆盖率和区间宽度都得到了明显改善，说明采用分解算法降低数据复杂度确实可以提高预测的效果；与同为分解算法的小波分析和经验模态分解相比，本文模型的预测精度和区间覆盖率更高，区间宽度更窄，虽然运行时间有所延长，但仍在可接受的范围内。考虑到预测效果改善的程度，这种运行时间的牺牲是值得的。综上所述，本文所提的EMD-RVM模型可实现短期风功率的区间预测，预测效果较好，可适用于实际工程应用。

5结论

为了更好地描述风功率的随机波动性，顾及电网运行中的不确定性，本文提出了一种基于集合经验模态分解和多核相关向量机的短期风功率区间预测方法。首先为降低数据复杂度，采用EEMD算法将风功率序列分解为多个频率不同的分量，然后采用多核RVM模型对各分量分别建立预测模型实现区间预测，再由各分量的预测结果进行叠加获得一定置信度下的区间预测结果。算例结果表明：本文模型不仅显著提高了预测精度，还在保证区间覆盖率的前提下，明显缩小了预测区间的宽度。因此，本文模型具有较高的预测准确度与较好的鲁棒性，可应用于工程实际。

参考文献：

[1] 王建东，汪宁渤，何世恩，等.国际风电预测预报机制初探及对中国的启示[J]. 电力建设，2010，31(9) ：10-13.

WANG Jiandong，WANG Ningbo，HE Shien，et al. International Wind Power Forecasting Mechanism and Some Lessons for China[J]. Electric Power Construction，2010，31(9) ：10-13.

[2] 党宏涛，杜祖良，任宏文，等.基于Bootstrap方法的平台惯导系统标定参数重复性区间预测[J]. 中国惯性技术学报，2013，21(3)：411-414.

DANG Hongtao，DU Zuliang，REN Hongwen，et al. Repeatability Interval Prediction for Calibrated Parameters of INS Based on Bootstrap Method[J]. Journal of Chinese Inertial Technology，2013，21(3)：411-414.

[3] 王焱，汪震，黄民翔，等.基于OS-ELM和Bootstrap方法的超短期风电功率预测[J]. 电力系统自动化，2014，38(6)：14-19.

WANG Yan，WANG Zhen，HUANG Minxiang，et al. Ultra-short-term Wind Power Prediction Based on OS-ELM and Bootstrap Method[J]. Automation of Electric Power Systems，2014，38(6)：14-19.

[4] BREMNES J B.Probabilistic Wind Power Forecasts Using Local Quantile Regression[J]. Wind Energy，2004，7(1)：47-54.

[5] 李智，韩学山，杨明，等.基于分位点回归的风电功率波动区间分析[J]. 电力系统自动化，2011，35(3)：83-87.

LI Zhi，HAN Xueshan，YANG Ming，et al. Wind Power Fluctuation Interval Analysis Based on Quantile Regression[J]. Automation of Electric Power Systems，2011，35(3)：83-87.

[6] 李知艺，丁剑鹰，吴迪，等.电力负荷区间预测的集成极限学习机方法[J]. 华北电力大学学报，2014，41(2)：78-88.

LI Zhiyi，DING Jianying，WU Di，et al. An Ensemble Model of the Extreme Learning Machine for Load Interval Prediction[J]. Journal of North China Electric Power University，2014，41(2)：78-88.

[7] 杨明，范澍，韩学山，等.基于分量稀疏贝叶斯学习的风电场输出功率概率预测方法[J]. 电力系统自动化，2012，36(14)：125-130.

YANG Ming，FAN Shu，HAN Xueshan，et al. Wind Farm Generation Forecast Based on Componential Sparse Bayesian Learning[J]. Automation of Electric Power Systems，2012，36(14)：125-130.

[8] 董雷，周文萍，张沛，等.基于动态贝叶斯网络的光伏发电短期概率预测[J]. 中国电机工程学报，2013，33(增刊)：38-45.

DONG Lei，ZHOU Wenping，ZHANG Pei，et al. Short-term Photovoltaic Output Forecast Based on Dynamic Bayesian Network Theory[J]. Proceedings of the CSEE，2013，33(S)：38-45.

[9] 孙斌，姚海涛，刘婷.基于高斯过程回归的短期风速预测[J]. 中国电机工程学报，2012，32(29)：104-109.

SUN Bin，YAO Haitao，LIU Ting.Short-term Wind Speed Forecasting Based on Gaussian Process Regression Model[J]. Proceedings of the CSEE，2012，32(29)：104-109.

[10] KHOSRAVI A，NAHAVANDI S，CREIGHTON D. Prediction Intervals for Short-term Wind Farm Power Generation Forecasts[J]. IEEE Transactions on Sustainable Energy，2013，4(3)：602-610.

[11] 韩帅，李树刚. 基于区间预测模型的流感趋势预测[J]. 计算机仿真，2014，31(9)：237-242.

HAN Shuai，LI Shugang.Influenza Trends Forecast Based on Interval Prediction Model[J]. Computer Simulation，2014，31(9)：237-242.

[12] QUAN H，SRINIVASAN D，KHOSRAVI A.Short-term Load and Wind Power Forecasting Using Neural Network-Based Prediction Intervals[J]. IEEE Transactions on Neural Network and Learning Systems，2014，25(2)：303-315.

[13] 孙志刚，翟玮星，李韦伦，等.基于EMD和相关向量机的短期负荷预测[J]. 电力系统及其自动化学报，2011，23(1)：92-97.

SUN Zhigang，ZHAI Weixing，LI Weilun，et al. Short-term Load Forecasting Based on EMD and RVM[J]. Proceedings of the CSU-EPSA，2011，23(1)：92-97.

[14] 叶林，刘鹏.基于经验模态分解和支持向量机的短期风电功率组合预测模型[J]. 中国电机工程学报，2011，31(31)：102-108.

YE Lin，LIU Peng. Combined Model Based on EMD-SVM for Short-term Wind Power Prediction[J]. Proceedings of the CSEE，2011，31(31)：102-108.

[15] 王守相，王亚旻，刘岩，等.基于经验模态分解和ELM神经网络的逐时太阳能辐照量预测[J]. 电力自动化设备，2014，34(8) ：7-12.

WANG Shouxiang，WANG Yamin，LIU Yan，et al. Hourly Solar Radiation Forecasting Based on EMD and ELM Neural Network[J]. Electric Power Automation Equipment，2014，34(8)：7-12.

[16] WU Z H，HUANG N E.Ensemble Empirical Mode Decomposition：a Noise-assisted Data Analysis Method[J]. Advances in Adaptive Data Analysis，2009，1(1)：1-41.

[17] 黄帅栋，卫志农，高宗和，等.基于非负矩阵分解的相关向量机短期负荷预测模型[J]. 电力系统自动化，2012，36(11)：62-66.

HUANG Shuaidong，WEI Zhinong，GAO Zonghe，et al. A Short-term Load Forecasting Model Based on Revelance Vector Machine with Nonnegative Matrix Factorization[J]. Automation of Electric Power Systems，2012，36(11)：62-66.

[18] 朱永利，尹金良.组合核相关向量机在电力变压器故障诊断中的应用研究[J]. 中国电机工程学报，2013，33(22)：68-74.

ZHU Yongli，YIN Jinliang. Study on Application of Multi-kernel Learning Relevance Vector Machines in Fault Diagnosis of Power Transformers[J]. Proceedings of the CSEE，2013，33(22)：68-74.

[19] GUAN C，LUH P B，LAURENT D M，et al. Hybrid Kalman Filters for Very Short-term Load Forecasting and Prediction Interval Estimation[J]. IEEE Transactions on Power Systems，2013，28(4)：3806-3817.

范磊(1991)，男，江苏常州人。在读硕士研究生，研究方向为电力系统负荷预测。

王越(1988)，女，江苏常州人。工学硕士，研究方向为微网负荷预测与规划。

梁智(1991)，男，江苏睢宁人。在读硕士研究生，研究方向为电力系统负荷预测。

(编辑阚杰)

Prediction on Short-term Wind Power Interval Based on EEMD-RVM

FAN Lei1, WANG Yue2, LIANG Zhi1, DAI Liyuan1

(1.The College of Energy and Electrical Engineering, Hohai University, Nanjing, Jiangsu 210098,China; 2. State Grid Changzhou Power Supply Company, Changzhou, Jiangsu 213000, China)

Abstract：In allusion to the problem of being unable to describe randomness of wind power by present wind power prediction methods, which are mostly aiming at certain point prediction, a prediction model for short-term wind power interval based on ensemble empirical mode decomposition (EEMD) and relevance vector machine (RVM) is established. It firstly conducts EEMD on original wind power sequence to obtain a remaining component and multiple intrinsic mode functions (IMFs) with different characteristics, then respectively establishes interval prediction model for each function by using RVM algorithm, and finally overlays prediction results for getting the interval prediction result under a certain confidence level. Simulation results indicate that the proposed interval prediction method has higher prediction precision, relatively narrow interval width and higher interval coverage.

Key words：short-term wind power prediction; interval prediction; relevance vector machine (RVM); ensemble empirical mode decomposition (EEMD); combined kernel function

作者简介：

中图分类号：TM614

文献标志码：A

文章编号：1007-290X(2016)02-0014-07

doi:10.3969/j.issn.1007-290X.2016.02.003

基金项目：国家高技术研究发展计划(863计划)资助项目(2013AA050601)

收稿日期：2015-09-28