具有年龄结构的三种群捕食与被捕食系统的最优边界控制

卜 红 彧

(辽东学院师范学院数学系，辽宁 丹东 118003)



具有年龄结构的三种群捕食与被捕食系统的最优边界控制

卜 红 彧

(辽东学院师范学院数学系，辽宁 丹东 118003)

[摘要]研究了一类具有年龄结构的三种群非线性捕食系统的最优边界控制问题，由Mazur定理得到了最优边界控制的存在性，利用法锥概念给出了最优控制满足的条件.

[关键词]捕食系统；年龄结构；最优边界控制；最优条件

1预备知识

对单种群动力系统最优控制问题的研究具有重要的应用价值，且已获得了较为系统的成果.[1-3]但对于多种群系统控制问题的研究，因其复杂性，尚不够完善.已有主要成果如下:文献[4-5]讨论了具有年龄结构的捕食-食饵种群动力系统的最优收获控制；文献[6-8]研究了具有年龄结构的竞争种群系统的适定性及最优控制问题；文献[9]讨论了具有空间扩散和年龄结构的三种群捕食与被捕食系统的最优收获问题；文献[10]讨论了具有年龄结构的两种群非线性竞争系统的最优边界控制.本文将在此基础上，讨论三种群捕食与被捕食系统的最优边界控制问题.考虑如下数学模型：

(1)

其中：Q=(0，A)×(0，T)，A为种群最大年龄，T为时间周期；pi(r，t)为第i个种群的分布密度；μi，βi分别为第i个种群的平均死亡率和平均生育率；λi为种群间的相互作用系数；pi0是第i个种群的初始分布密度；Pi(t)为第i个种群t时刻的种群总量；Si(t)为第i个种群t时刻的加权总量；wi(r，t)为权函数；fi是种群的外部扰动函数，如迁移等；控制变量vi(t)为r=0时的边界函数.

考虑如下的最优边界控制问题

(2)

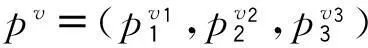
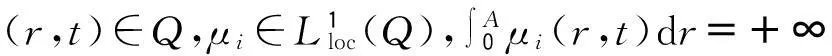
(H2) 对(r，t)∈Q，βi∈L∞(Q)；若s∈R+，对任意(r，t；s)∈Q×(0，+∞)，0≤βi(r，t；s)≤C1(C1为正常数)，βi关于s两次连续可微，偏导数有界且是不减的.

(H3)λi∈L∞(Q)，0≤λi(r，t；s)≤C2，这里C2为正常数.

(H4)pi0(r)∈L∞(0，A)，0≤pi0(r)≤C3，0≤w(r，t)≤C4，这里C3，C4为正常数.

(H5) 0≤fi(r，t)≤Ki，(r，t)∈Q，Ki为正常数，i=1，2，3.

定义1所谓系统(1)的解，是指存在函数p=(p1，p2，p3)∈L∞(Q；R3)且满足方程(1).

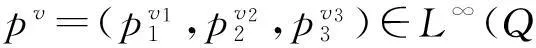
2最优边界控制的存在性

证明设

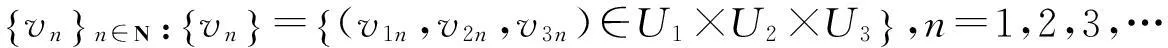
(3)

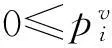
(4)

(5)

根据文献[11]中引理5.1.1知

(6)

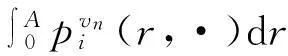
(7)

由(6)与(7)式及极限的唯一性得

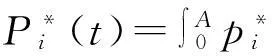
(8)

同理可推得

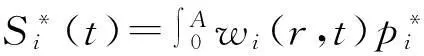
(9)

因Ui(i=1，2，3)有界，则U1×U2×U3中存在一个子序列，仍记为{(v1n，v2n)}，当n→∞时

(10)

(11)

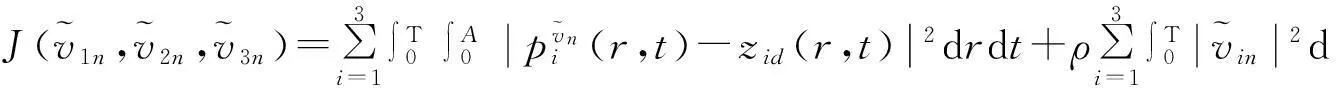
(12)

由J的凸性知

(13)

在(13)式中令n→∞，再由(3)式得

(14)

而显然有

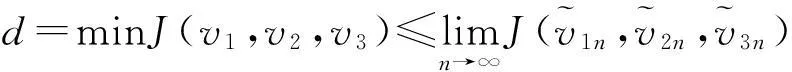
(15)

由(11)、(14)及(15)式得

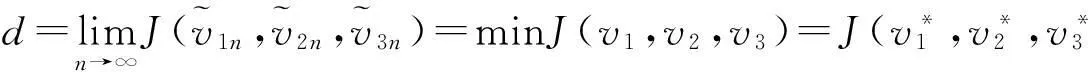
(16)

由(5)、(6)、(9)式及假设(H1)、(H2)得：

(17)

(18)

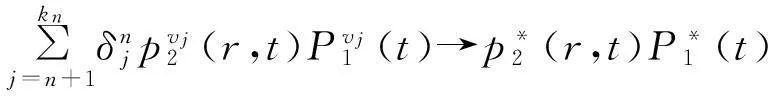
(19)

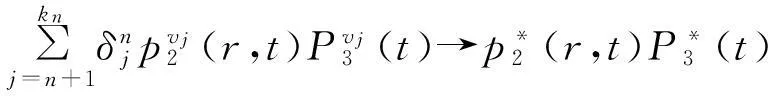
(20)

(21)

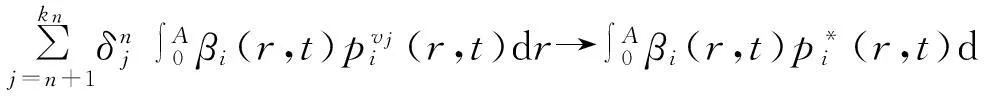
(22)

(23)

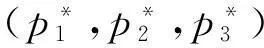
3最优条件

在不影响问题讨论的实质性的前提下，假设种群的外部扰动函数fi(r，t)=0，i=1，2，3.

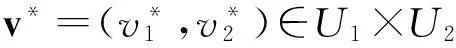
(24)

其中qi为下列对偶系统的解：

(25)

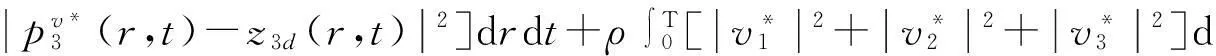
上式移项整理并两端同除以ε，取ε→0+的极限得

(26)

(27)

将(27)式中第一式两边乘以q1(r，t)并在Q上积分，利用(25)式中第四、五式，(27)式中第五式有

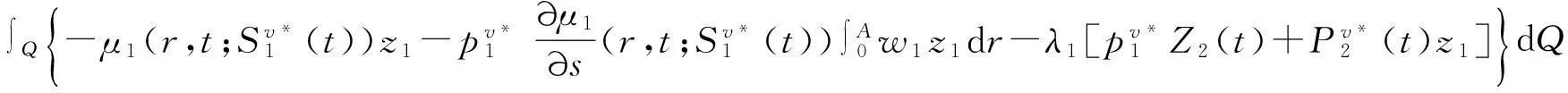
将(25)式中第一式代入上式，并注意到(27)式中第四式，

(28)

同理将(27)式中第二、三式分别乘以q2(r，t)、q3(r，t)，在Q上积分，并将(25)式中第二、三式分别代入得：

(29)

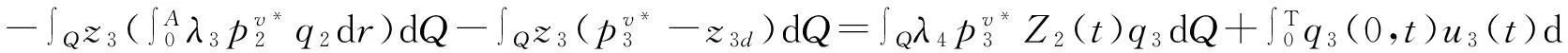
(30)

将(28)、(29)、(30)式相加，并注意到(27)式中第六式，有

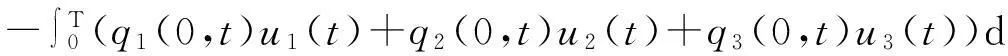
(31)

将(31)式代入(26)式可得(24)式成立.定理证毕.

综合上面的结果，我们有如下结论.

[参考文献]

[1]戴晓娟，张启敏.随机种群扩散系统最优边界控制的充分必要条件[J].宁夏大学学报(自然科学版)，2009，30(1)：18-21.

[2]付军，闫淑坤，吕显瑞.年龄相关的时变种群系统最优边界控制计算的惩罚移位法[J].吉林大学学报(理学版)，2010，48(2)：177-182.

[3]雒志学，王绵森.具有年龄结构的线性周期种群动力系统的最优收获控制问题[J].数学物理学报，2005，25A(6)：905-912.

[4]何泽荣. 具有年龄结构的捕食种群系统的最优收获策略[J].系统科学与数学，2006，26(4):467-483.

[5]雒志学.具有年龄结构的捕食-食饵种群动力系统的最优收获控制[J].数学的实践与认识，2007，37(12)：115-120.

[6]孙宏雨，赵春.具有年龄结构三竞争种群系统的适定性[J].天津师范大学学报(自然科学版)，2011，31(2)：1-5.

[7]FISTER K R，LENHART S. Optimal control of a competitive system with age-structure[J]. J Math Anal Appl，2004，291:526-537.

[8]赵坚，高夯.抛物系统的最优初值控制问题[J].东北师大学报(自然科学版)，2015，47(3)：1-4.

[9]顾建军，卢殿臣，王晓明.具扩散与年龄结构的三种群捕食与被捕食系统的最优收获[J].数学的实践与认识，2008，38(22)：101-108.

[10]卜红彧.年龄相关的两种群非线性竞争系统的最优边界控制[J].郑州大学学报(理学版)，2013，45(3)：20-24.

[11]ANITA S.Analysis and control of age-dependent population dynamics[M].Dordrecht :Kluwer Academic Publisher，2000：39-118.

(责任编辑：李亚军)

Optimal boundary control for an age-dependent predator-prey population dynamics of three species

BU Hong-yu

(Mathematics Department of Teacher’s College，Eastern Liaoning University，Dandong 118003，China)

Abstract:The optimal boundary control for an age-dependent predator-prey population dynamics of three species is investigated. The existence of the optimal boundary control is obtained by Mazur’s theorem and the optimal condition is deduced by means of normal cone.

Keywords:predator-prey population dynamics；age-dependence；optimal boundary control；optimal condition

[中图分类号]O 231.4[学科代码]110·47

[文献标志码]A

[作者简介]卜红彧(1981—)，女，硕士，讲师，主要从事分布参数系统控制研究.

[基金项目]辽宁省科技计划项目(W2011162)；中国高等教育学会“十一五”教育科学研究规划课题项目(06AIG0200048)；辽东学院青年基金资助项目(2014Q19).

[收稿日期]2014-10-15

[文章编号]1000-1832(2016)01-0039-05

[DOI]10.16163/j.cnki.22-1123/n.2016.01.010