二水平因子设计混合偏差新的下界
李洪毅,欧祖军,黎奇升
(1.吉首大学师范学院,湖南 吉首 416000;
2.吉首大学数学与统计学院,湖南 吉首 416000)
二水平因子设计混合偏差新的下界
李洪毅1,2,欧祖军2,黎奇升2
(1.吉首大学师范学院,湖南 吉首 416000;
2.吉首大学数学与统计学院,湖南 吉首 416000)
[摘要]混合偏差是在已有的偏差下提出的一种新的偏差,它克服了中心化L2偏差和可卷L2偏差的一些不足. 混合偏差作为部分因子设计的均匀性测度,寻找它的精确下界非常重要. 获得了二水平设计混合偏差的一个新的下界,数值例子说明它比已有的下界在某些设计中更加精确.
[关键词]U型设计;因子设计;混合偏差;下界
1预备知识
均匀设计是一种稳健的试验设计,它要求试验点均匀地遍及整个设计空间.[1]偏差是用来度量试验点分布的均匀性,具有最小偏差的设计称为在这个偏差下的均匀设计.目前常用的偏差有可卷L2偏差,中心化L2偏差等.[2]但由于可卷L2偏差,中心化L2偏差在我们所研究领域中出现了一些不足,Zhou,Fang和Ning[3]提出了一种新的偏差即混合偏差.混合偏差作为新的均匀性测度,寻找它精确的下界是十分重要的.如果一个下界是可达的,我们就认为这个下界是比较好的,文献[3]给出了二水平因子设计在混合偏差下的一个下界.本文旨在获得二水平部分因子设计混合偏差下的一个新的下界,且通过数值例子说明这个下界在某些设计中比已有的下界更精确.
对于一个有n次试验,s个q水平因子的设计,若每一列取{0,1,…,q-1}中的元素,且这q个元素出现的次数相等,均为n/q次,则称该设计为U型设计,并记为U(n;qs).所有这样设计的集合记为μ(n;qs).[4]本文主要针对二水平U型设计进行讨论.


(1)
当d∈μ(n;2s)时,(1)式可以改写为:
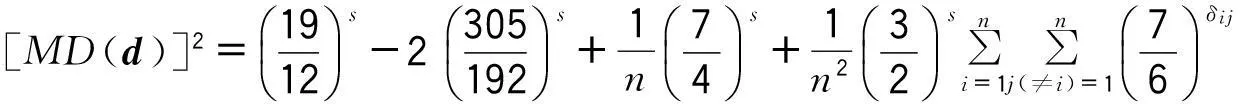
(2)
其中δij为设计d的第i行和第j行之间相应位置上相同元素的个数.
文献[3]根据二水平设计d∈μ(n;2s)的混合偏差与B准则的解析关系,给出了二水平因子设计的混合偏差的一个下界:
[MD(d)]2≥LMD1(d)=

(3)
其中sn,m=n(mod 2m).
引理1[5]对于任一U型设计d∈μ(n;2s),有

证明设n×s阶矩阵(α1,α2,…,αs)为设计d的设计阵,其中αk为设计d的第k列,k=1,2,…,s.由于d为U型设计,因此n是2的整数倍,即在αk中,元素0,1都出现n/2次,∀αk,它的第i行和第j行相应位置上的相同元素的个数记为δij(αk),则
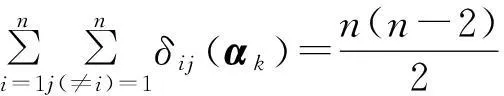
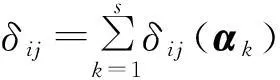
学生管理工作与教师自身素质分不开,有些教师受传统管理理念的影响,过分死板,忽视学生个体的发展需求,管理形式较为单一化和片面化。由于社会的进步,学校也在不断更新符合自身校园文化的学生管理制度,很多管理问题也随之出现,导致有时候很多管理问题得不到充分解决,大部分流于形式,执行不严,管理处于不规范、不稳定的状态。目前在学院“以学生为本”的全员育人环境还没有形成,很多学院的学生管理工作者对这一事业缺乏责任心,工作不积极,更多关注自己的事业,很少把心思放在学生身上,工作者思想体制不健全,缺乏学习交流的机会,导致思想能力跟不上制度的要求,管理制度效果不是很理想。

引理2[5]设l为任意正整数,d∈μ(n;2s).则

(4)
其中:w为(n-2)s/(2(n-1))的整数部分;p,q为满足p+q=k和pw+q(w+1)=r的整数部分;k=n(n-1);r=n(n-2)s/2.
证明设x1+x2+…+xk=r,且所有的xi都是非负整数.我们只需证明

构造Lagrange函数

其中λ为Lagrange乘数.对任意的1≤i≤k,





2主要结论
基于引理1和引理2,对任意的二水平U型设计d∈μ(n;2s),我们可得到[MD(d)]2新的下界.
定理1对任意的设计d∈μ(n;2s),有
[MD(d)]2≥LMD2(d).
其中

(5)
w,p和q如引理2所示.
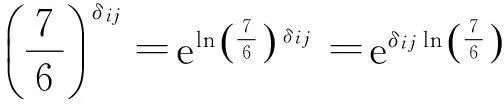
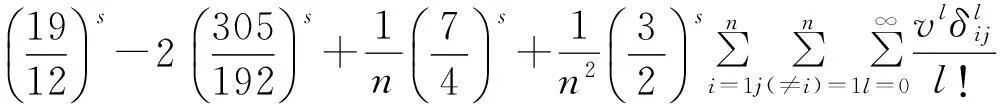
再由(4)式有
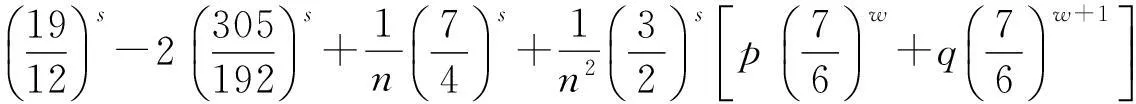
从而(5)式得证,定理证毕.
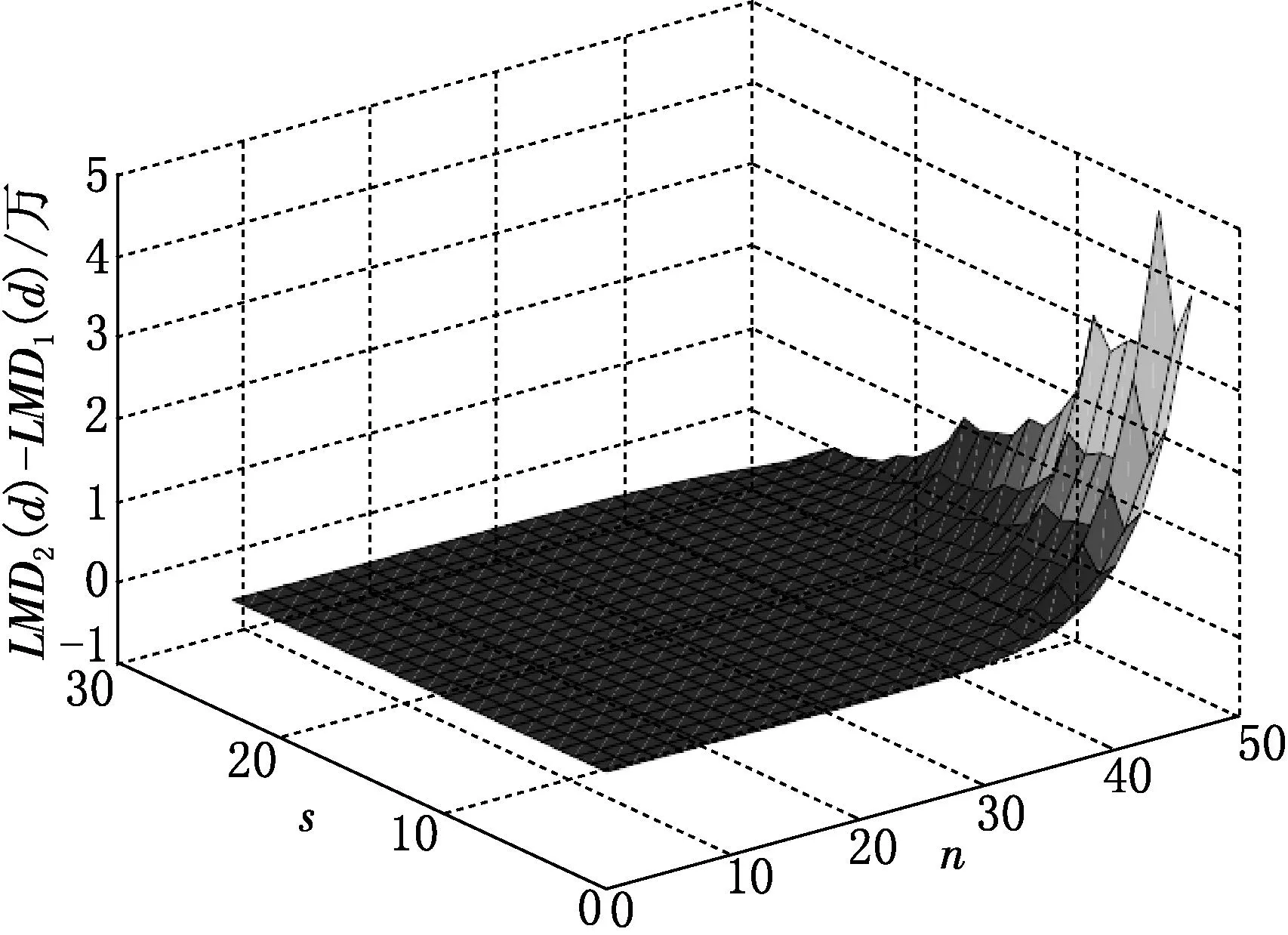
图1 LMD2(d)与LMD1(d)的差异
下面的图1反映了二水平因子设计混合偏差的两个下界的差异.从图1我们很容易发现有一部分LMD2(d)比LMD1(d)的值要大.
由(3)式和定理1我们可以给出任意二水平U型设计的混合偏差改进后的下界.
定理2对任意的设计d∈μ(n;2s),有
[MD(d)]2≥LMD(d).
其中LMD(d)=max{LMD1(d),LMD2(d)}.
3例子
下面我们用例子来验证我们的结论.
例1考虑Fang和Wink[6]的三个设计d8,4∈μ(8;24),d8,6∈μ(8;26),d8,7∈μ(8;27),其中n=8,s分别为4,6,7.表1分别给出了d8,4,d8,6,d8,7的设计表,混合偏差值的平方及相应的下界.

表1 二水平设计d8,4,d8,6,d8,7的设计表,混合偏差及其下界
例2考虑Fang和Winker[6]的两个设计d12,6∈μ(12;26),d12,12∈μ(12;212),其中n=12,s分别为6,12.表2分别给出了d12,6,d12,12的设计表,混合偏差值的平方及相应的下界.

表2 二水平设计d12,6,d12,12的设计表,混合偏差值及其下界
例3考虑下面的两个设计d6,9∈μ(6;29),d8,10∈μ(8;210).表3分别给出了d6,9,d8,10的设计表,混合偏差值的平方及相应的下界.

表3 二水平设计d6,9,d8,10的设计表,混合偏差值及其下界
对比表1,表2与表3的结果,我们不难发现:当试验次数n比因子个数s大得多时,第一个下界比第二个下界好,此时LMD1(d)>LMD2(d);当试验次数n与因子个数s比较接近或相等或n [参考文献] [1]FANG K T. Experimental design by uniform distribution[J]. Acta Mathematica Applicatae Sinica,1980,3:363-372. [2]HICKNELL F J. A generalized discrepancy and quadrature error bound[J]. Mathematics of Computation,1998,67:299-322. [3]ZHOU Y D,NING J H,FANG K T. Mixture discrepancy for quasi-random point sets[J]. Journal of Complexity,2013,29:283-301. [4]李华,白志东,肖玉山. 大维随机矩阵的渐进特征[J]. 东北师大学报(自然科学版),2014,46(4):1-8. [5]CHATTERJEE K,LI Z H,QIN H. Some new lower bounds to centered and wrap-aroundL2-discrepancies[J]. Statistics and Probability Letters,2012,82:1367-1373. [6]FANG K T,WINKER P. Lower bounds for centered and wrap-aroundL2-discrepancies and construction of uniform designs by threshold accepting[J]. Journal of Complexity,2003,19:692-711. (责任编辑:李亚军) A new lower bound to mixture discrepancy in two levels fractional factorial designs Li Hong-yi1,2, Ou Zu-jun2,Li Qi-sheng2 (1.Normal College,Jishou University,Jishou 416000,China;2.College of Mathematics and Statistics,Jishou University,Jishou 416000,China) Abstract:The mixture discrepancy is a new discrepancy based on existing discrepancy,which overcomes some weakness of the centered and wrap-round L2-discrepancies. As the measure of uniformity of fractional factorial designs,it is very important to look for the accurate lower bounds to the mixture discrepancy.This paper gives a new lower bound to the mixture discrepancy in two levels fractional factorial designs. The new lower bound is better than existing lower bounds in certain factorials designs. Finally,some examples are given to illustrate the results. Keywords:U type design;fractional factorial design;mixture discrepancy;lower bound [中图分类号]O 212.6[学科代码]110·6745 [文献标志码]A [作者简介]李洪毅(1978—),女,博士,讲师,主要从事统计学教学及概率统计研究;通讯作者:欧祖军(1979—),男,博士,副教授,主要从事计算机试验及试验设计研究. [基金项目]国家自然科学基金资助项目(11201177,11561025);湖南省教育厅优秀青年项目(14B146). [收稿日期]2014-06-23 [文章编号]1000-1832(2016)01-0034-05 [DOI]10.16163/j.cnki.22-1123/n.2016.01.009

