箱桁梁断面斜拉桥涡振性能及抑振措施的研究

冯　丛，华旭刚，胡腾飞，3，陈　强，陈政清

( 1．蒙西华中铁路股份有限公司，北京　100076; 2．湖南大学风工程与桥梁工程湖南省重点实验室，湖南长沙　410082; 3．广西交通科学研究院，广西南宁　530007)



箱桁梁断面斜拉桥涡振性能及抑振措施的研究

冯丛1，华旭刚2，胡腾飞2，3，陈强1，陈政清2

( 1．蒙西华中铁路股份有限公司，北京100076; 2．湖南大学风工程与桥梁工程湖南省重点实验室，湖南长沙410082; 3．广西交通科学研究院，广西南宁530007)

摘要:以在建的洞庭湖铁路三塔斜拉桥为工程背景，分析了箱桁断面斜拉桥主梁的建模方法以及涡激共振性能。首先比较了主梁建模的空间杆系模型、梁壳组合模型以及三维壳体模型在模态频率、主梁单位长度等效质量和等效质量惯性矩的差异。结果表明，三种模型的模态分析结果基本相近，但空间杆系模型不能准确得到高阶侧弯模态的主梁等效质量。继而采用刚性节段模型弹性悬挂风洞试验对箱桁组合主梁涡激共振性能进行了试验研究。研究表明，这类断面在－3°风攻角发生了超过容许幅值的竖向涡激共振，其中开口钢箱梁部分是诱发涡振的原因。最后进行了气动措施抑振试验，结果表明:在开口钢箱梁桥面板下缘设置两道下稳定板可以显著降低涡振振幅，即当稳定板高度为箱梁梁高一半时，涡振振幅降低至规范容许值以下;当稳定板高度与箱梁等高时，涡激振动现象消失。

关键词:铁路斜拉桥箱桁组合梁有限元建模涡激振动抑振措施风洞试验

采用钢箱钢桁组合梁作斜拉桥的主梁，相比传统的钢箱梁、钢桁梁及钢—混组合梁断面，具有刚度大、承载力高、桥面整体性好等优点，必将在未来大跨度斜拉桥主梁设计中得到广泛应用［1］。但与梁桥、拱桥相比，斜拉桥刚度较低，采用钢主梁体系时结构阻尼小，在风荷载作用下容易诱发明显的风致振动现象［2］。因此，建立一个准确的有限元模型，分析桥梁的动力特性，如模态频率、模态振型和模态质量等，是研究诸如桥梁抗风等动力问题的前提［3-5］。

颤振和涡激共振是典型的气动弹性现象。斜拉桥的扭转刚度大，因此颤振失稳临界风速通常很高。涡激共振(简称涡振)是大跨度桥梁在低风速下容易发生的一种限幅风致振动现象，涡激振动具有自激性质，只在特定的风速区间发生，并对结构阻尼及气动外形的微小变化十分敏感［4-5］。业界普遍认为，由细小杆件组成的桁梁断面难以形成规则脱落的漩涡，因而也就不易发生涡激振动。但是，对于新型的钢箱钢桁组合梁，可能发生涡激振动。涡振的控制措施可分为空气动力学措施与机械措施［6］。空气动力学措施主要通过设置或调整桥梁的附属结构，改变原结构的气动外形来改善主体结构周围的流场，从而达到控制涡激振动的目的;而机械措施主要通过增加结构阻尼来控制涡激振动。

本文以一座在建的三塔双主跨铁路斜拉桥为工程背景，对桥面系分别建立了主梁的空间杆系模型、空间板梁组合模型和空间板壳模型，分析和比较了这三套模型的模态特性、主梁单位长度等效质量及等效质量惯性矩。最后采用刚性节段模型弹性悬挂风洞试验对钢箱钢桁组合梁的涡振性能与抑振措施进行了试验研究。

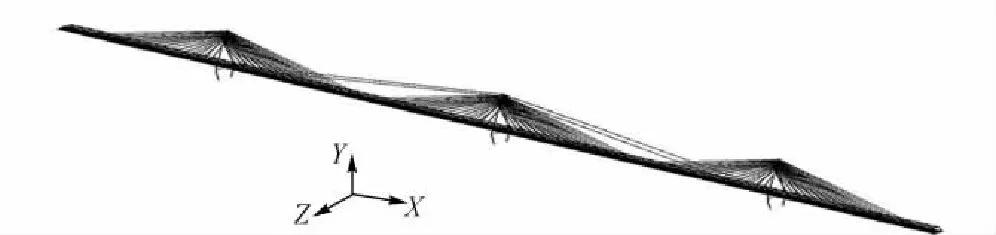
图1全桥有限元模型(空间板梁组合模型)

1桥梁有限元建模与动力特性分析

采用大型通用有限元软件ANSYS，对桥面系采用3种不同方法建立了该桥的有限元模型，分别为空间杆系模型(全部采用三维梁单元)、空间板梁组合模型(采用三维梁单元和板壳单元，见图1)及空间板壳模型(全部采用板壳单元)。同时考虑拉索垂度效应，采用Ernst公式对弹性模量进行修正后，利用分块Lancoz方法对该桥3种有限元模型进行了动力特性分析。分析时质量矩阵采用ANSYS默认设置(一致质量矩阵)，各阶振型按模态质量归一化。动力特性比较参见表1。

表1结构自振频率、模态振型、主梁等效质量或等效质量惯性矩

2主梁单位长度等效质量比较

由于主梁节段模型风洞试验中只对一定长度的主梁进行测振试验，而实际上桥塔、斜拉索等其他构件也会参与振动。因此，节段模型的单位长度等效质量，必须按考虑了实桥结构和振动三维空间特性的主梁等效质量来模拟［7］。为此，在结构自振特性分析基础上，计算了实桥在竖向、侧向和扭转方向上各模态对应的主梁等效质量和等效质量惯性矩。依据定义，实桥第i阶振型在主振动方向s( s = x，y，z，rotx)上的主梁单位等效质量和等效质量惯性矩为

式中:分子1为第i阶模态的广义质量(振型按质量归一化) ;φis为第i阶s方向的模态振型分量函数，模态振型提取时以单主梁节点或下弦杆节点的模态位移作为模态振型; Lg为主梁总长度。

主梁单位长度等效质量和等效质量惯性矩见表1。分析结果表明，3种模型的动力特性基本相近，空间板梁组合模型和空间板壳模型得到的模态频率、主梁单位长度等效质量和等效质量惯性矩基本相同，空间杆系模型不能准确得到高阶侧弯模态的主梁等效质量。考虑到空间杆系模型误差偏大，空间板壳模型计算量过大等因素，后续风洞试验将采用空间板梁组合模型的动力特性分析结果。

3　主梁节段模型涡振试验

3. 1试验参数

风洞试验需要满足几何参数、弹性参数、惯性参数、阻尼参数和黏性参数等相似准则。根据风洞试验段尺寸及实桥主梁断面大小确定几何缩尺比为1∶54. 5，节段模型横断面见图2，试验参数见表2。主梁节段模型涡振试验在湖南大学风工程试验研究中心HD-2边界层高速试验段进行，试验段风洞尺寸为17 m(长)×3. 0 m(宽)×2. 5 m(高)，试验风速范围0. 5～58 m/s。弹性悬挂刚性节段模型测振风洞试验见图3。

图2节段模型横断面(单位: mm)

表2节段模型试验参数

图3弹性悬挂刚性节段模型测振风洞试验

3. 2涡振限值

根据《公路桥梁抗风设计规范》规定，成桥状态下第一阶对称竖弯模态的涡激振动容许振幅峰值为

容许位移峰值

容许位移RMS(均方根)值

成桥状态下第一阶对称扭转模态的涡激振动容许振幅峰值为

容许位移峰值

容许位移RMS值式中: fh，ft分别为竖弯、扭转振动频率，B为箱梁宽度。

3. 3原断面试验结果分析

不采取任何控制措施时，该桥在阻尼比ξ= 0. 5%时的涡振试验结果见图4。结果表明:①各风攻角下都没有发生扭转涡振，+ 3°和0°风攻角下没有出现竖向涡激振动;②在－3°风攻角下，出现了明显的竖向涡激振动，风速锁定区间为15～18 m/s，最大涡振幅值均方根为0. 071 m，超过了《公路桥梁抗风设计规范》的容许值0. 049 m;③在锁定区间内，涡振频率与模型的竖向振动频率一致，为4. 785 Hz(见图5)。考虑到竖向涡振发生的条件处于桥梁正常运营范围之内，且极易发生涡振，因此，需要研究控制涡振的措施。

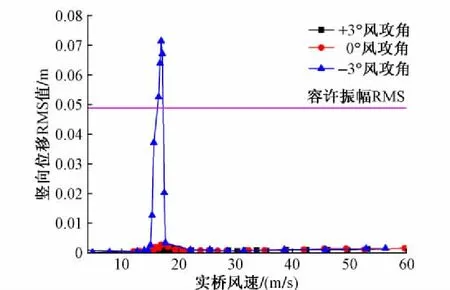
图4主梁竖向涡激振动(无控制措施)

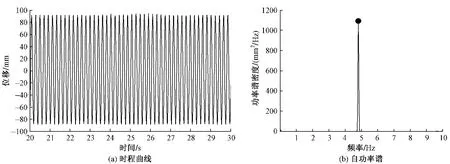
图5实桥风速16. 75 m/s时竖向涡激振动

按起振风速及下缘钢箱梁中心梁高( 2. 5 m)计算Sr( Strouhal)数

式中: f为漩涡脱落频率; D为物体垂直于来流方向平面上的特征尺寸，对于一般钝体截面，可取迎风面高度; U为层流风速。

由式( 6)可得到Sr = 0. 097，与开口断面钢箱梁Sr数值(≈0. 1)基本相同。如果取桁梁高度为迎风面高度(即取为14. 5 m)，则对应的Sr = 0. 561，由雷诺数(试验值Re≈2×107，实桥值Re≈2×107)与Sr数的关系曲线［8］可知，此时的漩涡脱落是随机无规律的脱落，不会产生具有周期性的涡激振动，这与试验事实相反。因此可以判断竖向涡激共振是由桁架以下的钢箱梁部分引起。

3. 4涡激振动控制

影响涡激共振的主要因素有:①来流湍流度，增加来流湍流度可以降低涡振振幅;②结构阻尼，涡激共振是典型的共振响应，增加阻尼可以大幅降低振幅;③结构的气动外形，通过改良断面绕流场，可以起到降低和抑制涡激共振的作用。考虑到该桥桥位湖面开阔，来流湍流度很低，因此重点对结构阻尼及气动措施的影响进行了试验研究。研究方案为:①研究多种典型阻尼比下的涡振振幅，获得涡振振幅对阻尼比的依赖性;②研究主梁气动措施方案，重点研究在正交异性桥面板下设置下稳定板的措施。

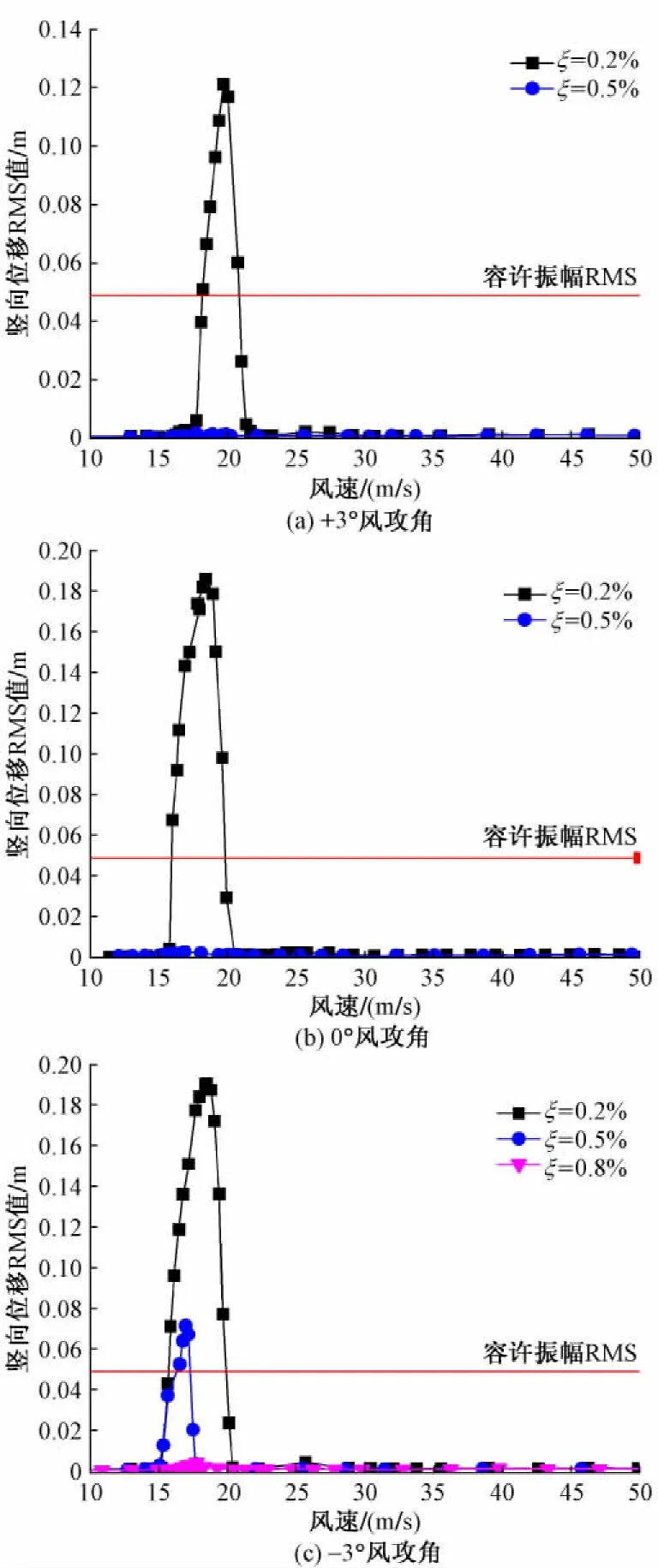
图6主梁竖向涡激振动(采取阻尼措施)

3. 4. 1阻尼措施

为获取涡振振幅对阻尼比的依赖性，采用不同阻尼比(ξ= 0. 2%，0. 5%，0. 8% )进行了涡振试验，试验结果见图6。结果表明:涡振对阻尼变化十分敏感，增加阻尼可以大幅降低振幅，阻尼比ξ= 0. 2%时，各风攻角下均出现涡振现象，且振幅均超过了《公路桥梁抗风设计规范》容许值;当风攻角为+ 3°时，起振风速为17. 6 m/s，振幅为0. 121 m，此工况为最有利工况;当风攻角为－3°时，起振风速为15. 0 m/s，振幅为0. 190 m，此工况为最不利工况。－3°风攻角工况还表明，阻尼比越高，涡振振幅与风速锁定区间越小，但对起振风速基本没有影响，当阻尼比增到一定量值时，可避免涡振发生。

3. 4. 2气动措施

从上述涡振分析知道，竖向涡激共振是由桁架以下的钢箱梁部分引起，故可以采用抑制开口钢箱梁断面涡振的方法加以控制，如增加下稳定板等措施。

在正交异性桥面板下约1 /4宽度位置的工字梁下端设置一对稳定板，稳定板与工字梁的总高分别为0. 25H( H为钢箱梁高度)，0. 50H(图7)，1. 0H，相应工况(阻尼比ξ= 0. 5% )下的试验结果见图8。研究表明:下稳定板对主梁涡振的抑制作用十分明显，当稳定板高度为梁高一半时，涡振振幅由0. 071 m大幅减小为0. 022 m，并能满足规范要求( 0. 049 m)，起振风速增大;当稳定板高度与梁等高时，涡振现象消失。因此，在不改变断面形状并能达到控制涡振目的的前提下，从工程实际出发，稳定板高度宜采用梁高的一半并布置于正交异性桥面板下约1 /4宽度位置的工字梁下端。

图7稳定板布置示意(板高为0. 5H)

4　结论

针对桥面系采用3种不同建模方法对荆岳铁路洞庭湖大桥动力特性和主梁单位长度等效质量(等效质量惯性矩)进行了分析和比较，并通过节段模型风洞试验对开口断面钢箱钢桁组合梁断面的斜拉桥进行了主梁涡激振动试验及抑制措施研究，得到如下几点结论:

1) 3种有限元模型的动力特性分析结果基本相近，空间板梁组合模型和空间板壳模型得到的模态频率、主梁单位长度等效质量和等效质量惯性矩基本相同，但空间杆系模型不能准确得到高阶侧弯模态的主梁等效质量。

2)不采取抗风措施时，该桥主梁断面在－3°风攻角、15～18 m/s风速区间内出现了明显的竖向涡激振动，其振幅超出了规范容许值。

3)在一定区间范围内，阻尼比越高，涡振振幅与涡振区间越小，但对起振风速影响很小，当阻尼比增到一定量值时，涡振现象消失。

4)下稳定板对涡振的控制效果比较明显，当稳定板高度为梁高一半时，涡振振幅大幅减小并能满足规范要求，起振风速增大;当稳定板高度与梁等高时，涡振现象消失。

5)综合工程实际及减振效果，稳定板宜采用梁高的一半。

参考文献

［1］高宗余．沪通长江大桥主桥技术特点［J］．桥梁建设，2014，44( 2) : 1-5．

［2］陈政清．桥梁风工程［M］．北京:人民交通出版社，2005．

［3］孙延国，廖海黎，李明水．基于节段模型试验的悬索桥抑振措施［J］．西南交通大学学报，2012，47( 2) : 218-223．

［4］何晗欣，李加武，周建龙．中央开槽箱形断面斜拉桥的涡激振动试验与分析［J］．桥梁建设，2012，42( 2) : 34-40．

［5］管青海，崔欣，王方亮，等．气动措施抑制钝体箱梁竖向涡振的风洞试验研究［J］．桥梁建设，2014，44( 1) : 56-62．

［6］葛耀君，丁志斌，赵林．缆索承重桥梁桥塔自立状态涡激共振及其控制［J］．同济大学学报(自然科学版)，2007，35 ( 8) : 1008-1012．

［7］朱乐东．桥梁涡激共振试验节段模型质量系统模拟与振幅修正方法［J］．工程力学，2005，22( 5) : 204-208．

［8］SIMIU E，SCANLAN R H．风对结构的作用:风工程导论［M］．刘尚培，译．上海:同济大学出版社，1987．

(责任审编孟庆伶)

Research on vortex-induced vibration and its control for cable-stayed bridge with box-truss composite girder

FENG Cong1，HUA Xugang2，HU Tengfei2，3，CHEN Qiang1，CHEN Zhengqing2

( 1．Mengxi-Huazhong Railway Co．，Ltd．，Beijing 100076，China; 2．Key Laboratory for Wind and Bridge Engineering of Hunan Province，Hunan University，Changsha Hunan 410082，China; 3．Guangxi Transportation Research Institute，Nanning Guangxi 530007，China)

Abstract:T he cable-stayed Dongting Lake railway bridge under construction was case-studied in this paper．A finite element modeling of the cable-stayed bridge with box-truss composite girder and its vortex-induced vibration were analyzed．T hree finite element schemes for modeling box-truss girder of the bridge，namely the spatial beam model ( SBM )，spatial plate-beam model( SPBM ) and spatial shell model ( SSM )，were compared in terms of modal frequency，equivalent mass and mass moment of inertia per unit length．It shows that the results from the SPBM and the SSM are basically the same，while the SBM can't accurately produce the equivalent mass unit length girder for some higher-order lateral modes．T he vortex-induce vibration of the box-truss composite girder was tested in wind tunnel by flexibly mounted rigid sectional model tests．T he results indicate that this cross-section type may experience large-amplitude vertical vortex-induced vibrations at wind attack angle of－3°，which is caused by the vortex shedding at the leading edge of the box-girder part of the cross-section．T he effects of aerodynamic appendix for suppression of vortex-induced vibrations were studied and it is found that two stabilizers beneath the open orthotropic deck dramatically reduce the vibration amplitude．T he vibration amplitude is within the limit given in design specification when the height of stabilizers is half of the box-girder height; and the vortex-induced vibrations completely diminish when the height of stabilizers is the same as the box-girder height．

Key words:Railway cable-stayed bridge; Box-truss composite girder; Finite element modeling; Vortex-induced vibration; Vibration control; W ind tunnel tests

文章编号:1003-1995( 2016) 02-0009-05

通讯作者:华旭刚( 1978—)，男，教授，博士。

基金项目:国家自然科学基金优秀青年基金项目( 51422806) ;国家自然科学基金项目( 51278189) ;中国铁路总公司项目( MHHTZX ［2013］0029-3)

收稿日期:2015-09-01;修回日期: 2015-11-20

中图分类号:U448．27

文献标识码:A

DOI:10．3969 /j．issn．1003-1995．2016．02．02

第一作者:冯从( 1979—)，男，高级工程师。