供应中断情况下基于备份供应商的应急决策分析
李新军,王建军,达庆利
(1.大连理工大学管理与经济学部,辽宁 大连 116024; 2.烟台大学经济管理学院,山东 烟台 264005;3.东南大学经济管理学院,江苏 南京 210096)
供应中断情况下基于备份供应商的应急决策分析
李新军1,2,王建军1,达庆利3
(1.大连理工大学管理与经济学部,辽宁 大连 116024; 2.烟台大学经济管理学院,山东 烟台 264005;3.东南大学经济管理学院,江苏 南京 210096)
在供应商—制造商二级供应链中,制造商作为领导者,采用一个战略供应商和一个备份供应商。有两种期权执行模式,一种是需求未知情况下提前向备份供应商订货的推式订货模式,另一种是获知需求后再向备份供应商订货的推式与拉式相结合的订货模式。证明了所建模型均为凸规划,并利用Karush-Kuhn-Tucker条件求得备份供应商的能力预定量、战略供应商订货量以及最优利润的表达式,得出了是否采用备份供应商的临界值。研究结果表明:推式模式下战略供应商的订货量较大,推拉结合模式下备份供应商的能力预定量较大,推拉结合模式下制造商的利润较大;随着战略供应商可靠性系数的增大,推式模式下首先放弃备份供应商的使用;当战略供应商的采购成本、备份供应商的期权执行成本和缺货成本较大,且残值以及可靠性系数较小时,推拉结合模式相对于完全推式的效果更加明显。
备份供应商;供应中断;能力期权;KKT条件;随机需求
1 引言
JIT精益化等先进生产方式和经济全球化给企业带来了巨大利润以及更高的运作效率,但同时也增大了供应链的脆弱性,突发事件一旦发生往往沿着供应链进一步蔓延和扩散,给企业带来巨大损失甚至破产。2000年,Ericsson公司的供应商Philips公司仅仅10分钟的半导体工厂起火,由此引起供应中断持续数周,导致Ericsson被迫退出手机市场。2011年,日本福岛大地震引起本田和日产等汽车公司的供应中断,导致他们部分生产线停工数月。近年来,我国也频繁发生突发事件,如2008年南方大面积冰冻灾害和四川汶川大地震,2010年青海玉树地震等,2014年上海福喜的食品质量安全事故。
Yu Gang等[1]认为,运作系统的内部因素和外部环境发生变化导致运作系统严重偏离原来的生产计划,并对系统的绩效造成巨大的损失和严重的不利后果,因此,必须采取相应的应急管理措施避免或者减缓突发事件的发生。傅克俊等[2]构建了以弹性策略和鲁棒性策略为核心的应急策略体系。姚杰等[3]利用动态博弈理论研究了突发事件发展变化的动态性特征以及采取阶段性处置措施后产生的应急预案和相应的效果。刘德海等[4]研究了高速公路突发事件下基于最小偏差组合权重的应急能力评价模型。萧海东[5]建立了大型运作系统中核心能力受损后进行应急恢复的应急管理脆弱性指标知识挖掘体系。Tomlin[6]研究了供应商发生供应中断时所采取的双源采购策略、应急库存策略和多产品的柔性订货策略的应急效果。李新军等[7]基于对供应商的影响范围将突发事件划分为系统性和个体性两类,基于奖惩激励机制和收入共享契约,研究了双源供应下突发事件相关性指数对供应应急运作管理的性能的响。通过对供应商的前期投资可以有效的降低供应中断发生的概率。Tang等[8]将供应可靠性系数作为内生变量,研究了制造商和供应商之间可靠性投资的分配机制,分别分析了供应完全中断和供应部分中断下单源供应和双源供应的应急运作策略。Kim等[9]研究了在突发事件发生前的预防和发生后的恢复两个阶段分别进行能力投资的供应应急运作机制。后备供应商也是降低供应中断影响的有效措施之一。Sting等[10]供应能力和顾客需求联合分布采用一个不可靠的主供应商和一个可靠的后备供应商,分别研究了自愿加入和强制加入约束下制造商与后备供应商之间的协调机制。这些文献主要从供应产出的随机性和需求的不确定性两个方面研究采取多源供应策略或求助后备供应策略解决供需不平衡或者干扰因素的应急管理措施,而缺少研究具体分析推式模式及推拉结合模式等不同运作模式下如何启用后备供应商应对供应中断问题。
期权合同的研究也成为供应链管理的研究热点之一。盛方正等[11]研究了市场上存在多种期权合同,购买者制定最优期权合同的充要条件。赵金实等[12]研究了期权定价市场化下逆向主导型供应链的运作策略和协调机制,分析了制造商的期权定价和供应商的产能设计。Cachon等[13]研究了供应商的生产成本作为公共信息和需求量作为制造商的私人信息的条件下的最优期权契约设计。Kleindorfer等[14]研究了期权合同供应市场和实时供货市场共存时,B2B交易模式下的资本密集型产业的最优期权合同。Victor等[15]研究了存在多个期权卖方时,期权购买者的最优订货策略。Wu等[16]研究了电子交易市场中期权合同供应市场和实时供货市场共存时,买方的最优采购策略和定价策略。这些文献主要研究期权合同和现货供应市场之间的相互关系和相互影响,而研究期权合同在供应应急管理中应用的却比较少,尤其没有涉及到制造商与后备供应商签订的最优期权合同。
近几年,有些学者研究了基于期权合同的应急管理问题。丁斌等[17]从合作博弈的角度,研究了政府提前支付部分货款和不允许缺货条件下,供应商储备一定量的应急物资的库存策略。田军等[18]研究了突发事件导致应急物流需求发生剧烈变化和现货市场价格随机波动情况下,政府运用实物期权协调与供应商的关系以便获得最佳的质量效果和成本效益。这两篇文献虽然研究了基于实物期权理论的应急采购,但是主要分析了由政府和供应商组成的非营利性供应链中的应急物资的实物储备和期权定价策略,没有涉及到营利性供应链的能力投资和基于战略供应商供应中断情况下与备份供应商之间的期权合约以及应急决策,也没有深入分析不同订货模式下的应急采购决策。
运用实物期权理论,分析制造商如何应对供应商的供应中断以及供应中断对制造商运作决策的影响,研究了制造商如何选择和制定合理的应急管理决策模式转移供应中断风险。由战略供应商、后备供应商和制造商所组成的二级供应链中,分析了制造商所采取的两种期权执行模式,一种是需求未知情况下提前向后备供应商订货的推式订货模式(简称N模式),另一种是获知需求信息后再向后备供应商订货的推式与拉式相结合的订货模式(简称Y模式)。
2 问题描述与符号说明
2.1 问题描述
假定制造商处于领导地位,一直使用一个由于可能发生突发事件面临着供应中断风险的战略供应商,为了降低供应中断造成的损失,同时存在一个在能力预订约束下满足任意订货量要求的完全可靠的后备供应商。制造商的运作流程是这样的:首先,制造商向后备供应商预订产能以便在不可靠的战略供应商发生供应中断时后备供应商能够提供不大于预定产能的所需供货量;接着,制造商向战略供应商发出订货,如果战略供应商没有发生突发事件则其供货量等于订货量,否则其供货量变为零;然后,制造商在后备供应商的能力预订约束下,决定向后备供应商的订货量,采用N模式和Y模式两种期权模式。整个决策过程如图1所示。

图1 基于供应中断的供应链各成员决策过程
2.2 符号说明
(1)战略供应商的供货量满足“all-or-noting”中断模式,正常供货的概率为γ,称之为可靠性系数,则供应中断概率为(1-γ);
(2)制造商向后备供应商的产能预订量为K,产能的单位预订成本为co,战略供应商正常供货时制造商向后备供应商的订货量为k1,战略供应商发生供应中断时制造商向后备供应商的订货量为k2,制造商向后备供应商订货时的单位执行成本为ce,假定向后备供应商预定一个单位能力并且执行一个单位的订货量的总成本co+ce为固定值;
(3)制造商向战略供应商的订货量为Q,单位订货成本为c,销售价格为p,单位产品残值为s,单位缺货成本为g,且c 另外,上标*表示最优值,上标′和上标〞分别表示一阶导数和二阶导数,下标N和Y分别代表推式订货模式和推拉订货模式。 决策 基于随机分布的顾客需求,当战略供应商和后备供应商的总供货量为M时,考虑到未销售产品的残值以及供大于求时所产生的缺货损失后,制造商所获得的收益为: (1) 基于子博弈精炼纳什均衡理论,采用逆向推导法,分两个步骤进行求解,首先确定后备供应商的订货量,然后同时确定战略供应商的订货量和后备供应商的能力预订量。 3.1 后备供应商的订货量 (1)战略供应商没有中断时后备供应商的订货量 战略供应商没有发生中断时供货量等于订货量Q,则制造商向后备供应商的订货量k1为: (2) (3) (4) (5) (2)战略供应商发生中断时后备供应商的订货量 战略供应商发生中断时则其供货量降为零,于是后备供应商的订货量k2为: (6) (7) (8) 3.2 战略供应商的订货量和后备供应商的产能预订量 战略供应商没有中断时,总供货量为Q+k1;战略供应商发生中断时,其供货量为0,只能依靠后备供应商供货,总供货量为k2。综合式(2)和(6),制造商获得的利润为: maxπ(Q,K)=γ[G(Q+k1)-cQ-cek1]+(1-γ)[G(k2)-cek2]-coK (9) maxπ(Q,K)=γ[G(Q+K)-cQ-ceK]+(1-γ)[G(K)-ceK]-coK (10) 若ce≥c,则: (11) (12) 若ce (13) (14) (15) 若ce≥c,则: (16) (17) 若ce (18) (19) maxπ(Q,K)=γ[G(Q)-cQ]+(1-γ)[G(K)-ceK]-coK (20) 若ce≥c,则: (21) (22) 若ce (23) (24) 3.3 本节小结 综合上一小节的情形1、情形2和情形3,基于全局最优和局部最优理论,可得: ①当ce≥c时,综合式(11)(12)(16)(17)(21)和(22),得: (25) (26) (27) (28) (29) (30) ②当ce (31) (32) (33) (34) (35) (36) 制造商在先向后备供应商订货后获知需求信息的推式模式N,战略供应商没有发生突发事件时,战略供应商和后备供应商的总供货量与只有一个完全可靠的供应商时的经典报童模型的订货量一致;当战略供应商发生供应中断时,只能靠后备供应商单独供货,ce≥c时其供货量与只有一个完全可靠的后备供应商时的经典报童模型一致,但当ce 定理1:当p+g-(ce+co-γmax(c,ce))/(1-γ)>0时,同时使用战略供应商和后备供应商;否则,放弃后备供应商,只使用战略供应商。 在由战略供应商、后备供应商和制造商所组成的二级供应链中,后备供应商的能力预定以及战略供应商的订货均采用推式订货,而后备供应商的实际订货采用拉式订货,即制造商对于战略供应商采用make-to-stock模式,而对于后备供应商采用make-to-order模式。 4.1 后备供应商的订货量 (1)没有发生中断时后备供应商的执行期权量 战略供应商没有中断时其供货量等于订货量Q,则制造商向后备供应商的订货量k1: (37) (2)发生中断时后备供应商的执行期权量 战略供应商发生中断时其供货量降低到零,则制造商向后备供应商的订货量k2: (38) 4.2 战略供应商的订货量和后备供应商的产能预订量 制造商的期望利润为: maxπ(K,Q)=ED{p[γmin((Q+K,D)+(1-γ)min(K,D)]-ce[γk1+(1-γ)k2]+sγ(Q-D)+-g[γ(D-K-Q)++(1-γ)(D-K)+]}-γcQ-coK (39) 销售残值只发生在战略供应商没有供应中断时,即d≤Q时,残值Q-d。缺货在两种情况下都可能发生,没有中断时若d>K+Q,缺货量为d-(K+Q);中断时若d>K,缺货量为d-K。将式(37)和(38)代入式(39),得: (40) 定理3:制造商的利润函数,即式(40),是凹函数。 (p+g-ce)[γ(1-F(Q+K))+(1-γ)(1-F(K))]-co=0 (41) (p+g-ce)(1-F(Q+K))+(ce-s)(1-F(Q))+s-c=0 (42) 以上分析了完全推式的N模式以及推拉结合的Y模式下,最优订货量,最优期权预定量,最优期权执行量,以及最优利润。下面比较分析这两种模式下的不同性能表现。 定理6:随着战略供应商可靠性系数的增大,完全推式的N模式,比推拉结合的Y模式放弃备份供应商的概率更大。 在供应商——制造商二级供应链中,制造商作为领导者,采用一个战略供应商和一个备份供应商。p=30,c=12,co+ce=16,g=12,s=5,γ=0.6,需求X服从[0,300]的均匀分布。分析参数ce,γ对战略供应商订货量、备份供应商预定能力以及制造商利润的影响。 期权执行成本ce从5(s=5)逐渐增大到16,即co从16逐渐减小到5,ce对战略供应商订货量、备份供应商预定能力以及制造商利润的影响如图2所示。可得如下结论: (1)Y模式下,战略供应商的订货量随着ce的增大而减小,备份供应商的能力预定量随着ce的增大而增大,而N模式下,战略供应商的订货量和备份供应商的能力预定量均取决于ce和c的相对大小,从而在这个临界点发生跳跃,总体趋势均是随着的ce增大而增大或不变; (2)N模式和Y模式下,制造商的利润均随着ce的增大而增大,且N模式下在ce=c这个临界点后增大较快,但不同模式之间的差距随着ce的增大而增大。 图2 N模式和Y模式下ce变化的影响趋势 根据ce与c的大小关系可分为两种情况(1)ce=14,ce>c,(2)ce=10,ce (1)随着γ的增加,战略供应商的订货量递增,而备份供应商的能力预定量越来越小,且在同一战略供应商可靠性系数γ下,N模式下战略供应商的订货量比Y模式大,且Y模式备份供应商的能力预定量比N模式大; (2)随着战略供应商可靠性系数γ的增加,Y模式和N模式下制造商的最优利润均越来越大,在同一战略供应商可靠性系数γ下,Y模式的最优利润比N模式大,两种模式之间的最优利润之差随着ce的增大而增大,随着战略供应商可靠性系数γ的增大而减小。 图3 N模式和Y模式下Q和K随γ变化趋势 图4 N模式和Y模式下π随γ变化趋势 进一步分析参数c,g,s,p对战略供应商订货量、备份供应商预定能力以及制造商利润的影响。得出如下结论: (1)不同参数对战略供应商的订货量的影响 N模式和Y模式下,参数s和c的影响趋势基本一致,战略供应商的订货量随着s的增大而增大,随着c的增大而减小;参数ce的影响正好相反,N模式下战略供应商的订货量随着ce的增大而增大,Y模式下随着ce的增大而减小;p和g的影响比较特殊并且趋势基本一致,Y模式下战略供应商的订货量随着p和g的增大而减小,N模式下依赖于ce和c的相对大小,ce>c时,战略供应商的订货量随着p和g的增大而增大,ce (2)不同参数对备份供应商的能力预定量的影响 N模式和Y模式下,参数p、g、ce、c和γ的影响趋势基本一致,备份供应商的能力预定量随着p、g、ce和cγ的增大而增大,随着γ的增大而减小;参数s的影响相反,N模式下备份供应商的能力预定量随着s的增大而增大,Y模式下随着s的增大而减小。 (3)不同参数对制造商的利润的影响 N模式和Y模式下所有参数的影响一致,制造商的利润随着ce、s、p和γ的增大而增大,随着c和g的增大而减小。 (4)不同参数对两种模式下制造商的利润差的影响 制造商的利润差随着g、c和ce的增大而增大,随着s和γ的增大而减小,随着p的增大趋于平稳。 (5)两种模式下运作性能的比较 N模式下战略供应商的订货量较大,Y模式下备份供应商的能力预定量较大,Y模式下制造商的最优利润较大;随着γ的增大,N模式放弃使用备份供应商的时间早于Y模式;随着p的增大,Y模式获利的时间早于N模式;备份供应商产能的利用率,N模式下ce 运用实物期权理论,研究了由面临供应中断的战略供应商、完全可靠的后备供应商以及制造商所构成的二级供应链中推式订货的N模式和推拉结合的Y模式。推式模式下战略供应商的订货量较大,推拉结合模式下备份供应商的能力预定量较大,推拉结合模式下制造商的利润较大;随着战略供应商可靠性系数的增大,推式模式下首先放弃备份供应商的使用;备份供应商产能的利用率,推式模式下备份供应商的期权执行成本小于战略供应商订货成本时最高,推式模式下备份供应商的期权执行成本大于战略供应商订货成本时最低,而推拉结合模式下居中;当战略供应商的采购成本、备份供应商的期权执行成本和缺货成本较大,且残值以及可靠性系数较小时,推拉结合模式相对于完全推式的效果更加明显。 本文中制造商与后备供应商之间的期权预定能力价格、期权执行价格以及战略供应商的采购价格均为外生变量,如果将它们作为内生变量,如何进行契约协调和决策分析,也是值得进一步研究的问题。 [1] Yu Gang, Qi Xiangtong. Disruption management: Framework, models and application [M].Fitchburg, MA: World Scientific Publishing Company, 2004. [2] 傅克俊, 胡祥培, 王旭坪. 供应链系统中的应急策略与模型[J]. 中国软科学, 2007(5): 119-124. [3] 姚杰, 计雷, 池宏. 突发事件应急管理中的动态博弈分析[J]. 管理评论, 2005,17(3): 46-51. [4] 刘德海, 于倩, 马晓南. 基于最小偏差组合权重的突发事件应急能力评价模型[J]. 中国管理科学, 2014,22 (11): 79-86. [5] 萧海东, 陈宁. 基于知识库的应急领域脆弱性指标体系研究[J]. 中国管理科学, 2014, 22(7): 76-81. [6] Tomlin B. On the value of mitigation and contingency strategies for managing supply chain disruption risks [J]. Management Science, 2006, 52(5): 639-657. [7] 李新军,季建华,王淑云. 供应中断情况下基于双源采购的供应链协调与优化[J]. 管理工程学报, 2014,28(3): 141-147. [8] Tang S Y, Gurnani H, Gupta D. Managing disruption in decentralized supply chains with endogenous supply processreliability [J]. Production and Operations Management, 2014, 23(7): 1198-1211. [9] Kim S H,Tomlin B. Strategic failure prevention and recovery capacity investments [J]. Management Science, 2013, 59(7): 1631-1649. [10] Sting F J, Huchzermeier A. Ensuring responsive capacity:How to contract with backup suppliers [J]. European Journal of Operational Research, 2010, 207(2): 725-735. [11] 盛方正,季建华. 最优期权合同组合的充要条件及采购方法[J]. 系统管理学报, 2008,17(3): 307-311. [12] 赵金实, 王浣尘, 郑晓涛. 期权定价市场化情况下逆向主导型供应链协调机制研究[J].管理工程学报2009,23(2): 111-115. [13] Cachon G P, Zhang Fuqiang. Procuring fast delivery:Sole sourcing with information asymmetry [J]. Management Science, 2006, 52(6): 881-896. [14] Kleindorfer P R, Wu D J. Integrating long and short term contracting via business to business exchange for capital intensive industries [J]. Management Science, 2003, 49(11): 1597-1615. [15] Victor M, David S. A portfolio approach to procurement contracts [J]. Production and Operation Management, 2005, 14(1): 90-114. [16] Wu D J, Kleindorfer P, Zhang J E. Optimal bidding and contracting strategies for capital intensive goods [J]. European Journal of Operational Research, 2002, 137(3): 657-676. [17] 丁斌, 桂斌. 基于合作博弈的预付条件下应急物资库存策略[J]. 运筹与管理, 2011,20(3):60-65. [18] 田军, 葛永玲, 侯丛丛. 政府主导的基于实物期权契约的应急物资采购模型, 系统工程理论与实践, 2014,34(10): 2582-2590. Decision Analysis of Backup Supplier for Supply Disruptions with Stochastic Demand LI Xin-jun1,2,WANG Jian-jun1,DA Qing-li3 (1. Faculty of Management and Economics, Dalian University of Technology, Dalian 116024,China;2. School of Economic and Management, Yantai University, Yantai 264005,China;3. School of Economic and Management, Southeast University, Nanjing 210096,China) During the last decade, to identify and mitigate supply disruptions is a topic that receives substantial management attention. Both diversifying supply sourcing including dual-sourcing and adding a backup supplier are logic ways to manage the risk of supply disruptions. There are two options execution modes. One is N mode that pushes ordering patterns, which means that the retailer orders from the backup supplier in advance under uncertain demand circumstances, the other is Y mode, push & pull ordering patterns, which means that the retailer doesn’t order from backup suppliers until he knows the demand circumstance. It’s successfully proved that the model is a convex programming through two options implementation strategy adopted by the retailer, and using Karush-Kuhn-Tucker conditions, a predetermined amount of backup suppliers, the closed expressions of optimal order quantity and profit expression can also be obtained. The threshold of using a backup supplier is given. By theorems and further numerical example, it can be concluded: Optimal profits is larger than primary supplier’s while primary supplier has larger order quantities under N mode, under Y mode, backup supplier’s capabilities predetermined amount. The impacts of model parameters on the ordering quantity from primary supplier are a little different based on the relative size ofceand c because of the execution of options. The capacity utilization of backup suppliers is highest whence backup supplier; supply disruptions; capacity options contract; KKT conditions; stochastic demand 1003-207(2016)07-0063-09 10.16381/j.cnki.issn1003-207x.2016.07.008 2014-10-09; 2016-03-03 国家社科基金资助项目(12CGL042);国家自然科学基金资助项目(71271039,71272122,71372122,71402158) 李新军(1975-),男(汉族),山东沂水人,烟台大学经济管理学院副教授,大连理工大学管理与经济学部博士后,研究方向:应急管理、物流与供应链管理,E-mail:lixinjun@dlut.edu.cn. F253 A
3 推式订货模式(N模式)下供应应急运作





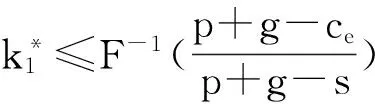


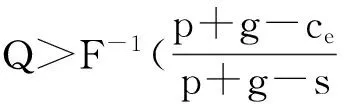
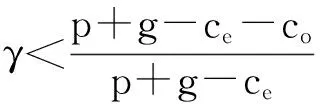

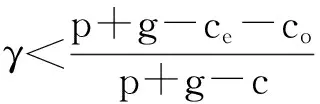


4 推拉结合模式(Y模式)下供应应急运作 运作决策


5 完全推式的N模式和推拉结合的Y模式 的性能分析

6 算例分析



7 结语

