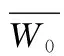允许直达的混合轴辐式快递网络规划模型与算法研究
赵 晋,张建军,严蔡华
(1.同济大学职业技术教育学院,上海 201804;2.同济大学中德工程学院,上海 201804;3.同济大学经济与管理学院,上海 200092)
允许直达的混合轴辐式快递网络规划模型与算法研究
赵 晋1,2,张建军3,严蔡华3
(1.同济大学职业技术教育学院,上海 201804;2.同济大学中德工程学院,上海 201804;3.同济大学经济与管理学院,上海 200092)
在快递企业的日常运营中,当两个城市之间的快递业务量达到一定规模之后会允许该城市对之间开展直达递送。但是这一规则通常仅在快递网络规划完成之后由相关子公司提请实施。为弥补这一实际规则的局部最优性缺陷,本论文将直达问题纳入网络规划决策,基于全局优化的视角构建了允许直达的混合轴幅式快递网络规划决策模型,设计了相应的求解流程,并对其中的指派关系决策构建了遗传算法。基于国内标杆企业的数值案例计算证明了该决策模型与求解方法的有效性,研究结果还说明,相对于纯轴辐式结构,允许直达的混合轴幅式网络结构有助于降低网络总成本,同时在直达线路上能够有效的降低迂回、提高服务时效性和服务水平。
快递网络;网络规划;直达线路;混合轴幅式网络;遗传算法
1 引言
当前,伴随电子商务、网络购物发展迅猛,我国快递服务业已进入高速发展期,2014年我国快递行业的日均处理量已超过3500万件,市场规模位居世界第一[1]。在企业界,2012年9月,FedEx和UPS两大国际快递巨头获得了经营中国国内快递业务的牌照;2013年5月,阿里巴巴集团宣布建立中国智能骨干物流网;2014年12月,国家邮政局批准雅玛多、欧西爱司、嘉里大通等物流经营国内包裹快递业务……从这些事件可以看到,当前,快递业的机遇与挑战共存,快递网络规划成为企业关注的焦点。
人们对网络规划问题研究的主要热点有[2-4]:(1)具有混合网络结构的网络规划问题;(2)具有网络建设固定成本的网络规划问题;(3)运输费用有折扣率的网络规划问题;(4)hub处理能力有限的网络规划问题;(5)大规模网络规划问题的求解算法设计。代表性的研究有:Rodriguez-Martin等[5]研究了包括hub边缘联接网络与环形网络在两层网络的规划中的作用,并设计了分支切割算法求解;Campbell[6]首次将服务时间作为约束条件纳入了与成本最小化为目标的网络规划模型,其中服务时间被转化为以距离的形式表达;作为一个发展,Alumura等[7]针对有时限约束的两层多式联运网络规划问题构建了一个混合整数规划模型,其中目标函数为线性函数、决策变量数量为O(n3)。赵宇哲[8]针对航运企业的重组与全球扩张引起的竞争问题,提出了竞争环境下的轴-辐式集装箱海运网络设计模型。张建军等[9]研究中国邮政速递物流公司的陆路网络规划问题,在多时限约束下提出了一个基于个体理性的启发式算法并构建了相应的决策支持系统等。傅少川等[10]设计了改进的禁忌搜索智能算法来求解无容量限制的单分配多枢纽中位问题模型。倪玲霖和史峰[12]分析了多分配快递轴辐网络的节点及连接关系、径路特征与形式等网络设计要素,在运输时间预算约束下以分拣费用、运输费用、中转费用之和为目标函数建立了多分配轴辐式快递网络枢纽选址与分配优化模型[11]。类似的对多分配结构[12]、逆向物流网络[13]等的研究。
与前述研究不同的是,我们的研究视角聚焦快递企业网络规划实践中的一类直达问题:在企业调研中,我们发现,企业管理者通常会有一条判断规则,即任何两个网络节点之间的快递流量如果达到了一定规模,则在其间开通一条直达运输线路。这一规则的价值是显著的,具有易于操作的优点,但是不足之处同样明显:它没有在全局优化的视角下分析其可行性。为此,本论文将允许直达纳入到快递网络规划问题中,探讨相应的决策模型和求解算法设计问题,为这一类具有重要实践价值的决策规则提供科学的方法指导。
2 问题描述
本文研究单一指派混合轴辐式网络结构,每个非枢纽节点指派给特定的枢纽中转站,同一子网或者不同子网之间的非枢纽节点可以有直达线路,各中转站之间两两直达运输。网络的结构图如图1。
如一批快件配送需求的发生地为货运站Si,目的地为货运站Sj,那么存在三种情况:
(1)直达线路(如果有的话):货运站Si→货运站Sj;
(2)同一区域内:货运站Si→枢纽中心Hk→货运站Sj;
换言之,货运站Si→枢纽中心Hk→枢纽中心Hk→货运站Sj;
(3)不同区域内:货运站Si→枢纽中心Hk→枢纽中心Hm→货运站Sj;
具体问题可以描述为:
(1)非枢纽节点都必须且只能与一个枢纽中心相连接;
(2)每个货运站只能单一指派给特定的枢纽中心,每个枢纽中心的覆盖区域内可以有多个货运站;
(3)网络中枢纽中心的数量为P;
(4)非枢纽节点之间可以直接相连;
(5)两个节点之间的流量运输只能有唯一的路径,不能将流量分成两个部分;
(6)枢纽节点之间全连通。
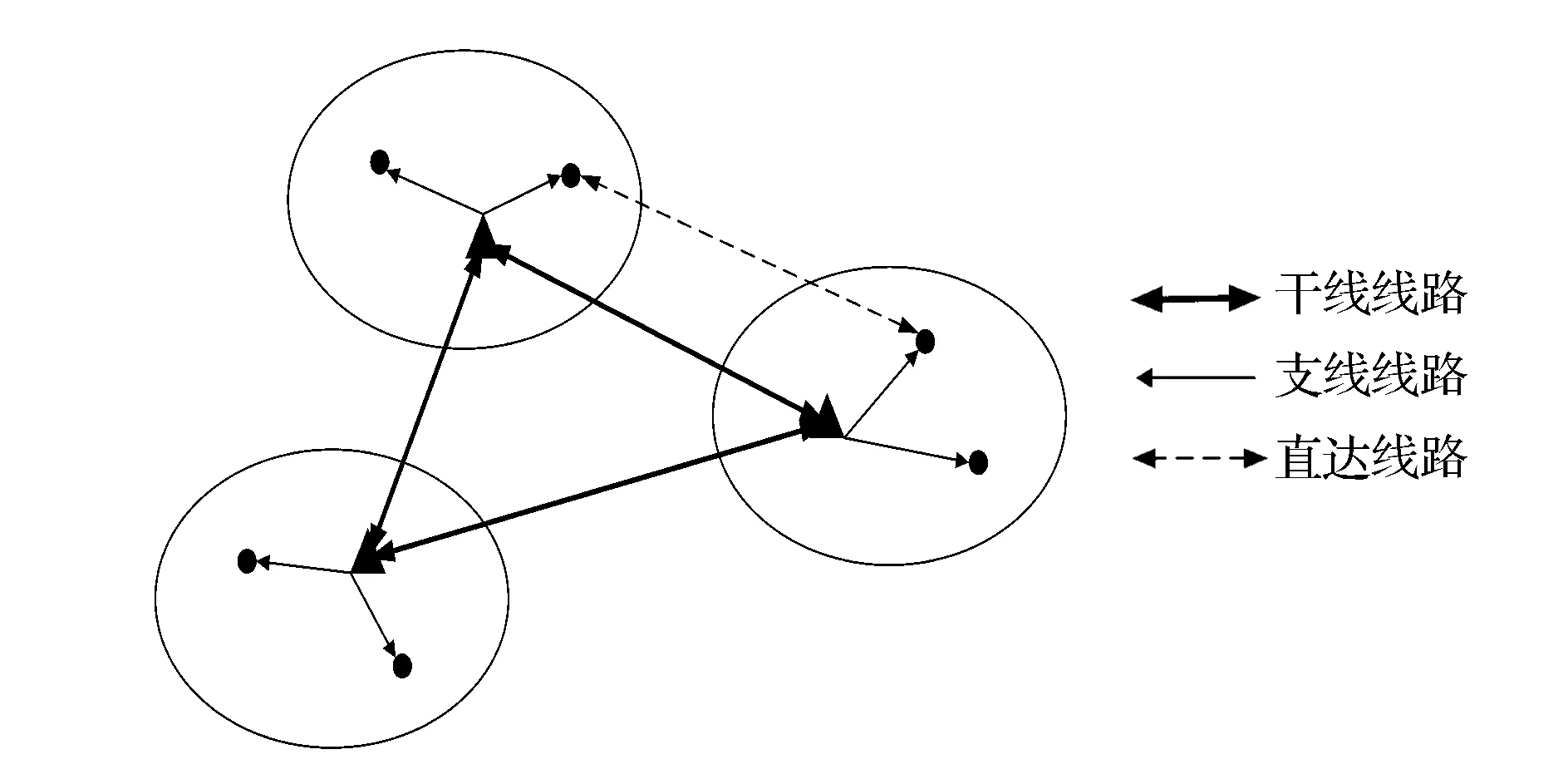
图1 允许直达的混合轴辐式网络结构
针对上述情况,需要解决如下几个决策问题:
(1)选取哪些节点作为枢纽中心点?
(2)每个枢纽节点的覆盖区域?各不同覆盖区域中非枢纽节点的货物运输路径?
(3)哪些非枢纽节点之间建立起直达运输路径?
3 决策模型构建
考虑一个混合轴辐式网络的完整集合G=(V,E),V表示节点(轴或者辐)的集合V={1,2,…,N},节点V表示的是网络中的起点和终点(如城市终端)以及可能的枢纽节点。E表示连接弧(轴辐中间的连接路径)的集合,E(i,j)的属性包括两点距离dij和从i运输到j的货物流量(体积或者重量)Wij,两点距离符合三角不等式规律。之前的文献中提到,任意两个节点对之间的物流运输包括通过E(i,k)从起点到hub的集货,经过hub点之间的转运E(k,m),经由E(m,j)配送到终点。本文规定,网络中任意一个起始终点对之间的正逆物流流量总和超过某一上限,那么就表明这两个城市节点之间的快递需求交互频繁,根据两点距离符合三角不等式规律,建立直达网络,而不是通过经过中转站运输,从而能够很好的满足城市对之间的物流需求的时效性要求。
传统的模型都是假设hub点之间是全连通的,每对hub点之间的流量运输都有成本折扣α,这是规模效益的具体体现。但是随之也带来一个问题,有时候hub点之间的运输流量并不比非hub弧上的流量要大,甚至更小。因此本文假设,当非枢纽节点之间满足建立起直达线路的条件时,规定该节点对之间的流量运输具有规模效应,折扣因子为β。
由于每个配送路径中通常包括三个环节:集货、转运和配送。本文将成本核算成如下表达形式:
Cij=χdik+αdkm+σdmj当货物通过转运中心转运时;
Cij=βdij当存在非枢纽节点之间的货物直达运输时。
通常规定χ=σ=1,0≤α<1,0≤β<1。
以网络运营成本最小化为目标,建立如下带有直达线路的混合轴辐式网络问题的模型:
(1)
约束条件:
(2)

(3)
Xi+δij≤1对于任意的i,j
(4)
δij=δji对于任意的i,j
(5)
Xk∈{0,1}对于任意的k
(6)
Xij∈{0,1}对于任意的i,j
(7)
δij∈{0,1}对于任意的i,j
(8)
参数说明:
α表示枢纽中心之间转运费用的折扣因子;
β表示直达路径上运输费用的折扣因子;
p表示需要建立的枢纽中心数量;
Cij表示节点对之间的单位运输费用;
Wij表示从起始点i到终点j的货物流量;
决策变量说明:
Xk为二进制决策变量,用于判断节点k是否为枢纽中心点;当Xk=1时,表示选择节点k作为枢纽中心;否则,Xk=0。
Xij为二进制决策变量,用于判断节点i是否与节点j相连通;当Xij=1时,表示节点i与j相连;否则,Xij=0。
目标函数说明:

约束条件说明:
式(2)限制了最终需要建立的枢纽中心点的个数;
式(3)、(7)保证了非枢纽节点只能与一个枢纽中心点相连;
式(4)、(5)是为了明确非枢纽节点间的直接通路与枢纽节点和非枢纽节点连接路径的区别;
式(6)、(7)、(8)是对决策变量取值的限制。
4 模型求解算法设计
上述所构建的混合轴辐式网络规划模型,在实践中由于网络节点数量较大,属于大规模的混合整数规划问题,如果采用精确求解的办法,通常很难或者根本不可能在可以接受的时间内得到问题的有效解。为此我们设计了一个分步启发式算法进行求解,首先将模型求解问题分成三个部分:枢纽选址问题,非枢纽点的直达路径构建问题,和非枢纽点的指派问题。我们设计的求解流程如图2。
4.1 枢纽中心选址
设计用于确定候选枢纽中心节点的求解过程如下:
第一步:计算节点i到其他与其有流量需求发生的节点的总运输距离和TCi;
第二步:计算节点i到其他各节点间的总流量之和TWi;
第三步:计算各节点的TWi/TCi值;
第四步:对所有节点的TWi/TCi值按从大到小排序,排位越靠前的节点被选中的几率越大,因为TWi/TCi值越大表明其运输流量大但运输总距离较小,体现了配送网络运营价值的最大化;
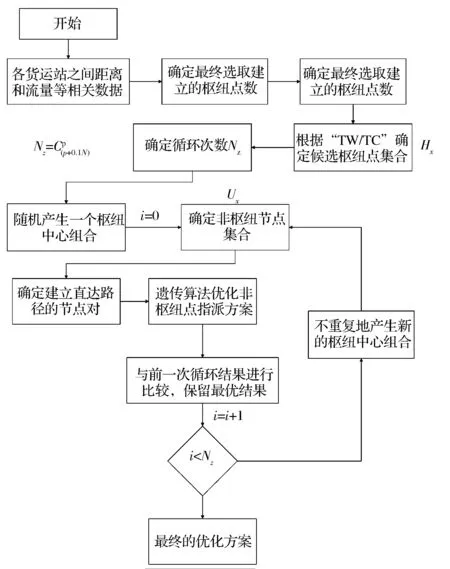
图2 决策模型的求解流程
4.2 非枢纽点的直达路径构建
设候选枢纽中心点得集合为H,非枢纽中心点的集合为U,则H+U=V,V是所有节点的集合。
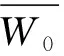
最终可以得到,在不同的枢纽中心点选址的情况下,非枢纽点中需要建立直接通路的节点对集合。
4.3 非枢纽点的指派
在前面两个部分完成之后,接下来就是要对非枢纽节点与相应的候选中心集合中的各个节点进行指派关系的确定。这是决策模型求解的核心部分。我们设计以下遗传算法,根据前面两个阶段确定的枢纽中心集合H和非枢纽中心集合U,通过算法的遗传搜索确定集合U中每个节点与集合H中的节点之间的指派关系,最终得到决策模型的解决方案。
(1)初始染色群体的设计
首先,将集合V(元素个数设为v)中的节点指派给距离最近的集合H(元素个数设为h,v+h=n)中的枢纽中心点,每个非枢纽节点只能指派给唯一特定的枢纽中心,若出现货运站节点到达两个枢纽中心点的距离相等的情况,则随机选取其中一个即可。如果将集合V中的v个非枢纽节点到集合H的h个枢纽中心的指派关系作为染色体的一个基因,那么整条染色体的基因个数将是v*h个,即一条染色体中有v段,每一段染色体有h个基因,h个基因的表示方式为二进制,1表示货运站指派给所在的染色体基因段的枢纽中心,0表示货运站不指派给所在的染色体基因段的枢纽中心。
例如:v=4,h=8,V=(1,2,3,4),H=(5,6,7,8,9,10,11,12)
染色体第一段,非枢纽节点到枢纽中心1的指派方式:

56789101112111000000
染色体第二段,非枢纽节点到枢纽中心2的指派方式:

56789101112200110000
染色体第三段,非枢纽节点到枢纽中心3的指派方式:

56789101112300001100
染色体第四段,非枢纽节点到枢纽中心4的指派方式:

56789101112400000011
通过设定染色体中的基因片段的不同的基因值,可以得到不同的染色体,组成初始染色体群。不同的染色体中基因片段和基因值各不相同,即相对应的非枢纽节点与枢纽节点之间的指派方案和整个运营网络不同,最终得出的运营网络总成本也不同,总成本最小的方案最优,总成本最大的方案最差。
(2)适应度函数设计
遗传算法在进化搜索过程中基本不利用外部信息,仅以适应度函数(Fitness Function)作为进化的依据,利用中群众每个个体的适应度来进行判断和搜索。适应度函数的选取至关重要,直接影响到遗传算法的收敛速度以及能否找到最优解。一般而言,适应度函数是由目标函数变换而来的。定义目标函数的方法,对于同一个问题而言,可能不止一种,选择时要尽量反应问题本身的整体特性,而不是只追求片面的目标。一般来说,适应度函数设计主要满足以下条件:
1)单值、非负、最大化;
2)合理、一致性。要求适应度函数值反应对应解的优劣程度。
3)计算量小。适应度函数设计要简单,减少计算时间和复杂性。
4)通用性强。适应度函数对某类问题,应尽可能通用。
运营网络的总成本可以通过染色体适应度的设定准确的反映出来,可以将染色体的适应度设为与运营网络总成本成反比例关系的值,即总成本越小,该染色体的适应度越高,反之则相反。为了达到在遗传选择过程中选取适应度较大的染色体概率较大和成本最小化的目的,因此适应度函数设定如下:

表1 20个战略重点城市
Fit(f(x))=M-f(x)
其中M为较大的常量,使得函数值非负。适应度函数将目标函数值转化成适应度,可以看出适应度越大,表明总成本越小,优化方案越好。
(3)选择操作设计
我们选用赌盘选择法进行选择运算,具体操作如下:
1)计算出群体中每个个体的适应度Fiti;
3)计算出每个个体被遗传到下一代群体中的概率pi,pi=Fiti/Fitzong
5)在[0,1]内产生一个均匀分布的伪随机数r;
6)若r≤q1,则选择个体1;否则,选择个体k,使得qk-1 7)重复5、6步骤共pop_size次,每次选出一个染色体,最终构成新的种群。 (4)交叉操作设计 我们采用多点交叉的方法来解混合轴辐式网络规划问题,主要有以下步骤: 1)设定交叉概率pc,循环次数Nc为:Nc=Chr_gene_size*pop_size*pc/2 其中:Chr_gene_size为每条染色体中基因个数; 2)在每一次的循环过程中,选取随机配对的染色体对进行基因交叉运算,从而产生新的个体,进而组成新的染色体群体。 (5)变异操作设计 变异过程主要有以下步骤: 1)设定变异概率pm,变异循环次数为Nd:Nd=Chr_gene_size*pop_size*pm 2)在每一次的变异过程中,随机选取一个染色体,随机选取该染色体中的任意基因点位进行变异,产生新的个体。 我们以国内某标杆快递公司的长三角区域陆路快递网络设计为例对上述决策过程的可适用性进行验证。 5.1 数据准备 本实例需要准备的基础数据如下: 1)城市节点数据:节点集合包括枢纽节点和非枢纽节点,如表1; 2)距离和流量数据:距离数据为每个节点对之间的距离,该距离矩阵为对称矩阵,由百度地图测得;流量数据为起始站到终点站在统计周期内的平均货流量,节点对之间的正逆向流量是不一样的,因企业保密问题,略去展示。 3)遗传算法基本参数数据:包括染色体种群大小、染色体基因数目、种群的最大进化代数、交叉概率、变异概率、适应度函数中的常量M、迭代次数,如表2。 表2 遗传算法参数设定 5.2 枢纽中心的确定 表3 确定的枢纽中心 表4 城市节点对的流量 至此,可以将案例中的城市节点分为两大类: 第一类,枢纽中心点集合:上海、苏州、杭州、南京; 第二类,非枢纽节点集合:常州、合肥、淮安、嘉兴、金华、连云港、南京、南通、宁波、绍兴、台州、温州、无锡、徐州、盐城、扬州、镇江。 5.3 非枢纽节点之间直达路径的确定 通过数据整理,得到表4。 由表4,根据流量阈值判断,可以得出7对直达线路:常州——南通、南通——宁波、南通——无锡、盐城——宁波、盐城——台州、盐城——无锡、扬州——温州。 5.4 非枢纽节点指派路径的确定 基于节4.3所设计的遗传算法,采用Matlab 7.0对网络节点的指派问题进行了编程,针对本案例的20个节点的问题规模进行求解,最终得出全局近似最优解如表5、6所示。 表5 求解所得的各项成本 表6 各枢纽中心的覆盖情况 5.5 结果分析 我们同样计算了不允许直达线路存在的网络结果,如表7所示。通过表6和表7的对比我们可以发现,在允许直达线路存在时,网络总成本比不允许情形减少了约0.79%。另一方面,由于减少了迂回,7对直达线路的存在能够显著提高它们的服务效率和服务水平。 表7 不允许直达时的成本 本文在允许直达的情形下建立了相应的混合轴辐式快递网络规划决策模型和决策流程,在保证时效性要求的前提下,以网络成本最小化为目标,对带有直达线路的轴辐式网络的规划问题进行了分析和数学描述,并设计了遗传算法对关键问题进行求解。进而,基于实际的企业运营数据的实证研究证明了该决策模型和方法的有效性,并且发现:允许直达时,网络成本能得到控制,并提高服务效率。 另一方面,本文研究存在以下不足之处尚需后续做进一步研究: (1)只考虑两个层级的混合轴辐式网络设计,如果能够综合考虑3个层次甚至更多轴辐式网络,将更加贴近实际,能够更好地指导实际应用; (2)本文初步考虑了以成本为目标的优化模型,并进行了模型求解,可以尝试采用多目标优化模型,加入相应的时间约束,这方面的研究将是今后进一步探讨的重点; (3)在算法设计中,本文首先确定了枢纽中心的个数和选址,这对成本最小化目标有一定的影响;根据相关文献,可以从全局最优的角度出发,以成本最小化为目标,让算法自动求解出相应的枢纽中心个数和选址,从而给出全局最优解,等。 [1] 国家邮政局.国家邮政局公布2014年邮政行业运行情况[EB/OL].[2015-01-15].http://www.spb.gov.cn/dtxx_15079/201501/t20150115_410741.html,2014. [2] Campbell J F, O'Kelly M E. Twenty-five years of hub location research[J]. Transportation Science, 2012,46(2): 153-169. [3] Contreras I, Fernández E. General network design: A unified view of combined location and network design problems[J]. European Journal of Operational Research, 2012, 219(3): 680-697. [4] Alumur S, Kara B Y. Network hub location problems: The state of the art[J]. European Journal of Operational Research, 2008, 190 (1): 1-21. [5] Rodriguez-Martin I, Salazar-Gonzalez J, Yaman H.A branch-and-cut algorithm for two-level survivable network design problems[J]. Computers & Operations Research, 2016, 67(c):102-112. [6] Campbell J F. Hub location for time definite transportation[J]. Computers & Operations Research, 2009, 36(12): 3107-3116. [7] Alumura S A,Yamanb H, Kara B Y. Hierarchical multimodal hub location problem with time-definite deliveries[J]. Transportation Research Part E: Logistics and Transportation Review, 2012, 48(6): 1107-1120. [8] 赵宇哲.竞争环境下的轴-辐式集装箱海运网络设计问题[J].中国管理科学,2015,23(7):103-112. [9] Zhang Jianjun, Tang Ou, Zhao Jin, et al.CPEL redesigns its land express network[J]. Interfaces,2013,43(3):221-231. [10] 傅少川,胡梦飞,唐方成.禁忌搜索算法在单分配多枢纽轴辐式物流网络中的应用[J].中国管理科学,2012,20(3):145-151. [11] 何明珂,程红晶.快递企业航空货运网络的构建[J].运筹与管理,2013,22(6):232-242. [12] 倪玲霖,史峰.多分配快递轴辐网络的枢纽选址与分配优化方法[J].系统工程理论与实践,2012,32(2):441-448. [13] 熊中楷,方衍,张聪誉.以旧换新收购方式下的逆向物流网络优化设计[J].中国管理科学,2011,19(6):65-72. Research on Hybrid Hub-spoke Express Network Decision with Point-to-point Direct Shipment ZHAO Jin1,2, ZHANG Jian-jun3, YAN Cai-hua3 (1.Institute of vocational education, Tongji University, Shanghai 201804, China;2.China-German School of Engineering,Tongji University, Shanghai 201804, China;3.School of Economics and Management, Tongji University, Shanghai 200092, China) express network; network design; point-to-point direct shipment; hybrid hub-spoke network; genetic algorithm 1003-207(2016)11-0058-08 10.16381/j.cnki.issn1003-207x.2016.11.007 2015-06-06; 2016-02-25 国家自然科学基金资助项目(71102071, 71373180);上海市社科规划课题(2014BGL025) 张建军(1978-),男(汉族),江西人,同济大学经济与管理学院副教授,博士生导师,研究方向:物流与供应链管理,E-mail:zhangjianjun@tongji.edu.cn. F272 A5 求解算法设计与案例计算




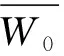



6 结语